Shanghai University
Article Information
- Hui CHENG, Tianyou FAN, Hao WEI
- Solutions for hydrodynamics of 5-and 10-fold symmetry quasicrystals
- Applied Mathematics and Mechanics (English Edition), 2016, 37(10): 1393-1404.
- http://dx.doi.org/10.1007/s10483-016-2133-9
Article History
- Received Jan. 22, 2016
- Revised Apr. 1, 2016
2. School of Science, Hebei Engineering University, Handan 056038, Hebei Province, China
The quasicrystals in binary and ternary alloys have been observed since 1982 firstly by Shechtman et al.[1]. Then, the natural quasicrystals were also found[2]. These can be named solid quasicrystals. After 20 years, soft-matter quasicrystals were observed in liquid crystals, colloids, and polymers, respectively by different research groups[3-7].
Soon after the discovery of the novel phase of solid and soft matter, the mechanical behavior was discussed (see Refs.[8]-[13]). The most important topics are elasticity[14-15] and hydrodynamics[16-19]. Due to the observation of soft-matter quasicrystals, the importance of hydrodynamics is more evident, though the hydrodynamics for soft-matter quasicrystals is different from that of solid ones.
In their pioneering work, Lubensky et al.[16] have created the theory of hydrodynamics of solid quasicrystals including the basic equations based on the Poisson bracket method of condensed physics, and comprehensively and in-depth studied hydrodynamic behavior of the phase. They especially explored the wave propagating nature of phonons and diffusive nature of phasons. They also explored the complete spectra of various hydrodynamic variables. Some material constants relating hydrodynamics were also estimated, which provide the real analysis on the motion of the medium at the time-space domain. At the early stage, the analysis was developed in the frequency-wave number domain (the Fourier transform domain) after the Fourier transform for the linearization of the governing equations. This helps us understand the dispersion relation and the spectra, which are very beneficial. It is well-known that the Fourier transform is an important tool. If one can obtain the solution at the frequency-wave number domain (the Fourier transform space), then making Fourier inversion can lead to the physical time-space domain solution. However, the inversion cannot be realized at present, due to the complexity of the equations even if in the linearized version. From the elastodynamics angle, Rochal and Lorman[20] suggested a simplest model of the hydrodynamics (in which the mass conservation equation and phonon dissipation equations were omitted), which was named the minimal model of phonon-phason dynamics, and discussed the solutions in the frequency-wave number domain (the Fourier transform space). This shows that the implementation for the time-space solution is necessary. Fan et al.[21] and Zhu and Fan[22] took the similar simplest model to Rochal and Lorman and solved the initial-boundary value problems in the physical time-space domain. Some numerical analyses were given. Though the simplified model and the relevant analyses at the time-space domain were significant, which partly described the effects of phonon-phason coupling and phason dissipation, they were not complete and did not explore the effects of viscosity, phonon dissipation, and mass density variation versus time. To improve the present situation, a complete analysis at the time-space domain based on the strict hydrodynamics equations of Lubensky et al.[16] is necessary.
The analysis in the time-space domain is more complicated than that in the frequency-wave number domain. The first problem is the solvability of the initial-boundary value problem of the equations, and the second problem is the specimen of the material for the computation, which includes not only initial conditions but also boundary conditions. Without these data, any computation would not be carried out, and any result cannot be obtained. These conditions must be consistent with the basic equations derived by Lubensky et al.[16]. Otherwise, the solution cannot be existent, unique, and stable, that is the solvability of the initial-boundary value problem. Therefore, these two problems are closely connected to each other. The governing equations of Lubensky et al.[16] on solid quasicrystals are novel nonlinear partial differential-variational equations. The mathematical physics on hydrodynamics has not been set up. The existence, uniqueness, and stability of solutions of the equations are the fundamental problems to be studied. Due to lack of the mathematical physics theory of hydrodynamics, the solving in this study is a probe at present only. We take a finite difference method to solve a proposed specimen of pentagonal/decagonal quasicrystal under two-dimensional configuration. To explore the dynamic behavior of the medium, we assume that it is subjected to a dynamic external loading. The computational results and some conclusions are listed in the following sections. The work quantitatively determines the displacement, velocity, and stress fields, describes the effects of hydrodynamic parameters, and explores the dynamic behavior of field variables, which may help us further understand hydrodynamics of solid quasicrystals, and provides a basis for experimental measurement and practical application of the matter.
2 Governing equationsThe governing equations of hydrodynamics of Lubensky et al.[16] are as follows. The mass conservation equation is
the momentum conservation equations are
the equations of motion of phonons due to symmetry breaking are
and the phason dissipation equations are
in which $\rho$ is the mass density, $u_{i}$, $w_{i}$, and $V_{i}$ are the phonon, phason, and velocity components, respectively, $\eta_{ijkl}$ is the viscosity coefficient tensor, and $\Gamma_{u}$ and $\Gamma_{w}$ are the phonon and phason dissipation coefficients, respectively. In addition, the Hamiltonian $H$ is defined as
The integral in Eq.(5) represents the contributions of momentum and variation of mass density to the energy, where $A$ and $B$ denote the material constants relating the variation of mass density. The last term belongs to the potential energy of phonon, phason, and phonon-phason coupling listed as follows:
where $C_{ijkl}$ and $K_{ijkl}$ are the phonon elastic constants and phason elastic constants, respectively, and $R_{ijkl}$ and $R_{klij}$ are the phonon-phason coupling elastic constants (refer to Ding et al.[23], Hu et al.[24], and Fan[25]). Meanwhile, we have the elasticity and viscosity constitutive laws,
where $\sigma _{ij}$, $H_{ij}$, and $\sigma _{ij}'$ denote the phonon, phason, and viscous stress tensors, respectively, and $\varepsilon _{ij}$, $w_{ij}$, and $\dot {\xi }_{ij}$ are the phonon elastic strain, phason elastic strain, and viscous deformation velocity tensors, respectively,
in which the super index $d$ of the integral element denotes the dimension of the space.
Equations (1)-(4) are the governing equations of motion of solid quasicrystals, which hold for all solid quasicrystals. Their solutions describe time and space variations of fields $\rho$, $V_{i}$ (or $\rho V_{i}$), $u_{i}$, and $w_{i}$.
To write explicit expression of Hamiltonian $H$ in Eq.(5), one must give the corresponding constitutive law, which will be given in Appendix A.
Equations (1) and (2) are the results of conservation laws, and Eqs.(3) and (4) are the results of symmetry breaking. Due to breath conservation laws, the derivation of the equations given by Lubensky et al.[16] utilizes the Poisson bracket method of condensed matter physics summarized by Dzyaloshinskii and Volovick[26], and Fan[27] gave some additional derivations. These novel nonlinear equations belong to the achievement of condensed matter physics as well as mathematical physics. There are huge difficulties for solving the equations. The difficulties come not only from the complexity of the equations but also from boundary conditions. It is well-known that the solutions of partial differential-variational equations strongly depend on the corresponding boundary conditions. In the following, we have to discuss the solution considering concrete boundary conditions.
Lubensky et al.[16] pointed out that the fields $u_i$ and $w_i$ play quite different roles in hydrodynamics. The relation $\frac{\partial u_i }{\partial t}\sim V_i $ shows that $u_i$ represents wave propagation, and there is no relation $\frac{\partial w_i }{\partial t}\sim V_i $ which indicates that $w_i$ is diffusive rather than oscillatory in physical nature. The equation set (1)-(4) is a wave-diffusion mixed type nonlinear equation system. Meantime, the global boundary conditions subjected to the equations are also mixed types, the solutions of the initial-boundary value problems exhibit the wave-diffusion coupling characters, and the apparent graphic of solution of $w_i$ does not exhibit pure diffusive profile such as appearing in the simplest diffusive equation, which will be introduced through the computational results in the following.
3 For two-dimensional case of pentagonal and decagonal quasicrystals, initial-boundary value problem and computational sample of decagonal Al-Ni-Co quasicrystalWe here discuss point group $5, \overline 5 $ pentagonal and point group $10, \overline {10}$ decagonal quasicrystals, and only for the plane field, i.e., the motion of the medium is in the $xy$-plane if the $z$-axis is taken as the 5- or 10-fold symmetry axis. In the case, the governing equations are the same for both point group $5, \overline 5 $ pentagonal and point $10, \overline {10}$ decagonal quasicrystals. All field variables depend only on the variables $x$, $y$, and $t$, and those of the $z$-component are vanished. If the terms ($\nabla_{i}(r)u_{j})\frac{\delta H}{\delta u_{j}}$ and ($\nabla_{i}(r)w_{j})\frac{\delta H}{\delta w_{j}}$ are omitted in Eq.(2), the governing equations (1)-(4) can be reduced to Eq.(9) as follows:
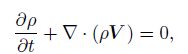 (9a)
(9a) 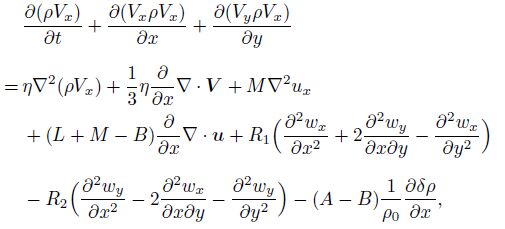 (9b)
(9b) 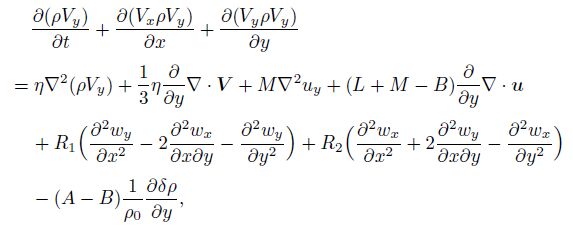 (9c)
(9c) 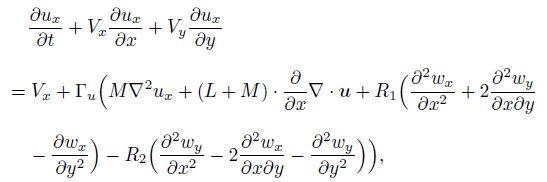 (9d)
(9d) 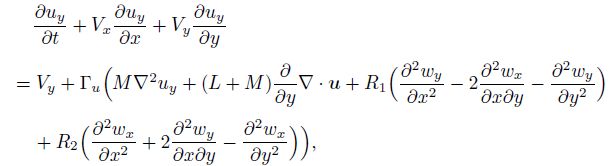 (9e)
(9e) 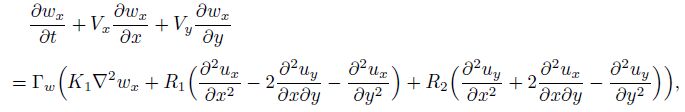 (9f)
(9f) 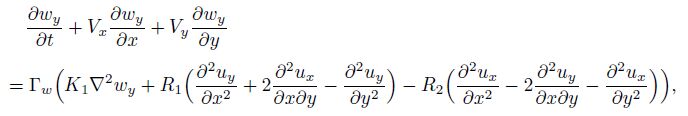 (9g)
(9g) in which $\nabla \cdot =i\frac{\partial }{\partial x}+j\frac{\partial }{\partial y}$, $V=iV_x + jV_y $, and $u=iu_x +ju_y $. The detail about the derivation of Eq.(9) was given by Fan.
To solve the equations at the physical time-space domain, the corresponding initial and boundary conditions must be given simultaneously. The more general discussion on the initial and boundary conditions of hydrodynamics of solid quasicrystals here has not been undertaken. We take a specimen shown by Fig. 1 and list the relevant conditions for the specimen.

|
| Fig. 1 Specimen of quasicrystal under impact loading with $A_1\, (10^{-4}$m, $10^{-4}$m) and $A_2\, (10^{-4}$m, $-10^{-4}$m) |
|
|
We assume that the specimen at the initial time is in rest. Therefore, there are the initial conditions
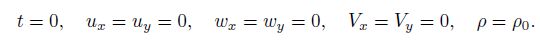 (10)
(10) At the surface of the specimen, there are the following boundary conditions:
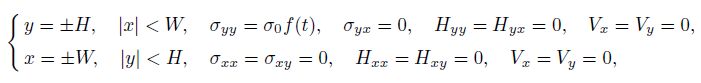 (11)
(11) in which $\sigma _0$ is a constant with the stress dimension, $f(t)$ is the function of time, which is taken as the Heaviside function, i.e., $f(t)=H(t)$. Of course, this loading is an idealized case. The boundary conditions designed belong to the simplest one for both numerical computation and further experimental measurement, in which the nonhomogeneous boundary condition is only for phonon stress, and the boundary conditions for the phason field and viscosity flow field are homogeneous. As an example, we calculate a decagonal Al-Ni-Co quasicrystal with the experimentally measured material data $\rho _0=4.186 8\times 10^{-3}$ g/mm$^3$, the viscosity coefficient $\eta =1\times10^{-4}$ cm$^2/{\rm s}$ (in addition, here $y$ is, in fact, the kinetic viscosity coefficient according to Ref.[6]), and the elastic moduli $C_{11} =2.343 0\times 10^{11}$ N/m$^2$ and $C_{12} =0.574 1\times 10^{11}$ N/m$^2$, which are obtained by the resonant ultrasound spectroscopy[25]. We also choose $K_1=1.22\times 10^{11}$ N/m$^2$ and $K_2=0.24\times 10^{11}$ N/m$^2$ estimated by Monte Carlo simulation[28] and $A=B=10^{9}$ N/m$^2$, $\Gamma _u =4.8\times 10^{-8}$ cm$^3\cdot$$\mu $s/g, and $\Gamma _w =4.8\times 10^{-10}$ cm$^3\cdot$$\mu $s/g[25]. The coupling constants $R_1 $ and $R_2$ have not been measured so far. In computation, we take $R_1/M=0.001$ and $R_2 /M=0.002$, where $M=(C_{11} -C_{12} )/2$, $\sigma _0 =5$ MPa, $H=20$ mm, and $W=10$ mm.
4 Numerical solution and resultsThe specimen shown in Fig. 1 is a simplest specimen for exploring the hydrodynamic behavior of the quasicrystal through computational analysis. The upper and lower surfaces of the specimen are subjected to impact external stress $\sigma _{yy} =\sigma _0 H(t)$, where the loading function is taken to be the Heaviside function
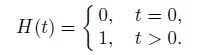 (12)
(12) Of course, this is an extreme case (at $t=0$, the loading rate is infinite).
Equation (9) under the initial and boundary value conditions (10) and (11) is named the initial-boundary value problem (9)-(11). This is a nonlinear initial-boundary value problem, because the partial differential equation set is nonlinear. We solve the initial-boundary value problem by a finite difference method. The numerical solutions with highly stability are obtained.
The impact loading at the upper and lower surfaces of the specimen is a disturbance source. If the initial propagating rate of the disturbance source is denoted by $v_0 $, which can be evaluated by $v_0 =\frac{H}{t_0 }$, where $t_0 $ is the time of propagation of the disturbance source to the central transverse section, the computational point is close to the location. The computation for time $t_0$ is easy which can directly check the computation.
In Fig. 2, the variation of mass density versus time is illustrated, which explicitly explores the wave propagation character of the physical process under the given boundary conditions of the specimen. Before reaching the wave emanated from the upper surface to the computational point $A_1$ whose distance to the upper surface is almost equal to $H$ (completely similar to the wave emanated from the lower surface to the computational point $A_2$), the mass density maintains its initial value $\rho _0 $, and the propagation time is equal to $t_0 =2.545 $$\mu $s, which is evaluated by $t_0 =\frac{H}{v_0}$ and $v_0 =\frac{H}{t_0 }=7.858 5$ km/s and is close to the value of the longitudinal wave speed $c_{\rm L} =\sqrt {(L+2M+A-2B)/\rho_0} =7.480 7$ km/s (for the formula of the longitudinal wave, refer to Lubensky et al.[16]). This is a direct check to the computation physically, though there is a smaller difference between the values of $v_0 $ and $c_{\rm L} $. It is understandable, because the longitudinal wave speed formula is a linear elastic result, and the present case is a nonlinear medium. The disturbance source propagating speed $v_0 $ from the upper surface to the computational point is not exactly equal to the linear longitudinal wave rate. However, these two values are close to each other. This shows that the mathematical formulation of the initial-boundary value problem is correct, the solving method is effect, and the solution presents satisfactory precise.

|
| Fig. 2 Variation of mass density of computational point $A_{1}$ (or $A_{2})$ of specimen versus time |
|
|
The phenomenon indicates that for the complex system of wave propagation and diffusion coupling, the phonon wave propagation plays a dominating role. At the moment that the wave arrives at the central, because the dynamic load is an impacting force which produces a tensile wave, the value of mass density at central section decreases steeply to the minimum.
After the longitudinal waves emanated from the upper and lower surfaces confluent each other at the central section, and the arrival of succeeded transverse wave and the reflected waves by lateral surfaces of the specimen, the material at the location is compressible, the absolute value of $\delta \rho /\rho _0 $ increases ($-$13 order of magnitude), and then $\rho $ grows into a maximum value 2.527 $\times $10$^{-14}$ at the time 8.149 $\mu $s indicating that $\rho $ is beyond the initial value $\rho _0 $.
Figure 3 gives the time variation of velocities (the velocities of mass point to the coordinates) at the point $A_1 $ in the $x$- and $y$-directions, respectively, in which the wave behavior is still exhibited. Before the propagation time $t_0 $, the values of velocities are zero. The order of their magnitude is $10^{-10}$ m/s for the material. This quantitatively explores the hydrodynamic character of the motion pointed out by Lubensky et al.[16]. Though one knows that the motion should be very slow, beforehand we did not know the realistic order of magnitude of the rate, and naturally there was no possibility to know the exact values of the rate. At that time, the analysis was only qualitative.

|
| Fig. 3 Velocity fields at computational point $A_{1}$ of specimen versus time |
|
|
Figure 4 illustrates the time variation of phonon displacements at the point $A_1 $ in the $x$- and $y$-directions, respectively. The results show the wave propagation behavior of the field variables, which is evident. Of course, the performance of $u_x $ and $u_y $ is different from each other, which is resulted from the boundary conditions and specimen configuration.

|
| Fig. 4 Phonon displacement fields at computational point $A_{1}$ of specimen versus time |
|
|
The results on the phason displacements $w_x $ and $w_y $ are plotted by Fig. 5. Their order of magnitude is much smaller than that of the phonons. This is understandable, because the external disturbance source comes from the phonon stress, and the corresponding phason boundary conditions are homogeneous (the zero boundary conditions). If we take the phonon stress boundary conditions homogeneous and the phason stress boundary conditions nonhomogeneous, then the order of magnitude of solutions of phasons is much greater than that of the present results. In addition, the phason displacement field represents diffusion rather than wave propagation in physical nature, but the profile of the figures of $w_x $ and $w_y$ does not exhibit pure diffusion feature which exhibited for solutions of simple diffusion equation due to the strong coupling of wave equations and the controlling of the mixed boundary conditions.

|
| Fig. 5 Phason displacement fields at computational point $A_{1}$ of specimen versus time |
|
|
Figures 6-8 show the time variation of phonon, phason, and viscosity normal stresses at the computational point. It is evident that the phonon stress is two order greater of magnitude than the phason one, and the phonon and phason stresses are much greater than the viscosity one. The outline of phason stress describes certain diffusive behavior, which is evidently different from that of phonon one, while the outline of phonon and viscosity ones exhibit typical wave propagation character and present strong oscillation.

|
| Fig. 6 Elastic normal stress at computational point $A_{1}$ (or $A_{2})$ of specimen versus time |
|
|

|
| Fig. 7 Phason normal stress at computational point $A_{1}$ (or $A_{2})$ of specimen versus time |
|
|

|
| Fig. 8 Viscosity normal stress at computational point $A_{1}$ (or $A_{2})$ of specimen versus time |
|
|
The illustrations in Fig. 9 depict the spatial variations of phonon displacements, viscosity velocities, and phason displacements of a quarter specimen at the time point $t=14 $$\mu $s. It is evident that these three kinds of fields exhibit quite different spatial configurations, because they represent quite different types of motion. The differences among their spatial distributions are understandable.

|
| Fig. 9 Spatial distributions of phonon displacements (a) and (b), viscosity velocity components (c) and (d), and phason displacements (e) and (f) of quarter of specimen at time point $t=14 $$\mu $s |
|
|
So far, for the initial and boundary value problems of hydrodynamics of solid quasicrystals, there is no theory on the existence, uniqueness, and stability of the solutions, unlike that in elasticity, where Guo and Fan[29] gave a proof from the point of view of weak solution. In spite of this, some initial-boundary value problems of nonlinear partial differential equations of hydrodynamics of solid quasicrystals are solvable if the problems are well-conditional. The practice shows that the computation is effective for other quasicrystal systems. Only the constitutive equations are replaced by corresponding equations. For example, if $R_1 =R$ and $R_2 =0$, then we obtain the solution for point group 5 m pentagonal and point group 10 mm decagonal quasicrystals. After appropriate derivation, we can obtain some similar equations to Eq.(9) for other quasicrystalline systems and corresponding initial and boundary conditions similar to Eqs.(10) and (11). The solutions for these quasicrystal systems can also be obtained.
The solutions for other specimens and other initial and boundary conditions through the numerical methods can also be obtained. Of course, the theory on existence, uniqueness, and stability of the initial-boundary value problems has not been proven up to now. The computation reported in the previous sections is only a probe, in which the computation is stable and presents higher precise.
The analysis leads to fruit quantitative results in the time-space domain on field variables of hydrodynamics ranging from mass density to fields of velocity, displacement, and stress of phonons and phasons. These results reveal that the phonon field is dominated in the physical process. Moreover, the coupling between phonon and phason fields is important. The effect of viscosity is very weak, in which the dissipation effects are also explored. This shows that hydrodynamics of Lubensky et al.[16] is a strict and complete theory with its physical basis in-depth. However, the computational results explore that the variation of mass density is very small (i.e., $\delta \rho /\rho _0 \sim 10^{-13})$, which shows that the material is incompressible in fact. Another problem is that the effect of solid viscosity is too weak, e.g., the viscous stresses $\sigma _{ij}' \sim 10^{-19}$ GPa which are smaller over 10 order of magnitude than the values of phonon stresses $\sigma _{ij}$ and phason stresses $H_{ij}$.
| [1] | Shechtman, D., Blech, I., Gratias, D., & Cahn, J.W Metallic phase with long-range orientational order and no translational symmetry. Physical Review Letters, 53(20), 1951-1953 doi:10.1103/PhysRevLett.53.1951 (1984) |
| [2] | Bindi, L., Steinhardt, P.J., Yao, N., & Lu, P.J Natural quasicrystals. Science, 324(5932), 1306-1309 doi:10.1126/science.1170827 (2009) |
| [3] | Zeng, X., Ungar, G., Liu, Y., Percec, V., Dulcey, A.E., & Hobbs, J.K Supramolecular dendritic liquid quasicrystals. nature, 428(6979), 157-160 doi:10.1038/nature02368 (2004) |
| [4] | Takano, A., Kawashima, W., Noro, A., Isono, Y., Tanaka, N., Dotera, T., & Matsushita, Y A mesoscopic Archimedean tiling having a new complexity in an ABC star polymer. Journal of Polymer Science Part B:Polymer Physics, 43(18), 2427-2432 doi:10.1002/(ISSN)1099-0488 (2005) |
| [5] | Hayashida, K., Dotera, T., Takano, A., & Matsushita, Y Polymeric quasicrystal:mesoscopic quasicrystalline tiling in ABC star polymers. Physical Review Letters, 98(19), 195502 doi:10.1103/PhysRevLett.98.195502 (2007) |
| [6] | Talapin, D.V., Shevchenko, E.V., Bodnarchuk, M.I., Ye, X., Chen, J., & Murray, C.B Quasicrystalline order in self-assembled binary nanoparticle superlattices. nature, 461(7266), 964-967 doi:10.1038/nature08439 (2009) |
| [7] | Fischer, S., Exner, A., Zielske, K., Perlich, J., Deloudi, S., Steurer, W., Lindner, P., & Förster, S Colloidal quasicrystals with 12-fold and 18-fold diffraction symmetry. Proceedings of the National Academy of Sciences, 108(5), 1810-1814 doi:10.1073/pnas.1008695108 (2011) |
| [8] | Fan, T.Y., & Fan, L Plastic fracture of quasicrystals. Philosophical Magazine, 88(4), 523-535 doi:10.1080/14786430801894536 (2008) |
| [9] | Li, W., Fan, T.Y., & Wu, Y.L Plastic analysis of crack problems in three-dimensional icosahedral quasicrystalline material. Philosophical Magazine, 89(31), 2823-2831 doi:10.1080/14786430903082014 (2009) |
| [10] | Fan, T.Y., Wang, X.F., Li, W., & Zhu, A.Y Elasto-hydrodynamics of quasicrystals. Philosophical Magazine, 89(6), 501-512 doi:10.1080/14786430802562157 (2009) |
| [11] | Li, X.F A general solution of elasto-hydrodynamics of two-dimensional quasicrystals. Philosophical Magazine Letters, 91(4), 313-320 doi:10.1080/09500839.2011.559179 (2011) |
| [12] | Li, X.F Elastohydrodynamic problems in quasicrystal elasticity theory and wave propagation. Philosophical Magazine, 93(13), 1500-1519 doi:10.1080/14786435.2012.745655 (2013) |
| [13] | Cheng, H., Fan, T.Y., Sun, J.J., & Wei, H Possible soft-matter quasicrystals of 5-and 10-fold symmetries and hydrodynamics. Computational Materials Science, 105, 47-54 doi:10.1016/j.commatsci.2015.04.012 (2015) |
| [14] | Bak, P Phenomenological theory of icosahedral incommensurate ("quasiperiodic") order in Mn-Al alloys. Physical Review Letters, 54(14), 1517-1519 doi:10.1103/PhysRevLett.54.1517 (1985) |
| [15] | Bak, P Symmetry, stability, and elastic properties of icosahedral incommensurate crystals. Physical Review B, 32(9), 5764-5772 doi:10.1103/PhysRevB.32.5764 (1985) |
| [16] | Lubensky, T.C., Ramaswamy, S., & Toner, J Hydrodynamics of icosahedral quasicrystals. Physical Review B, 32(11), 7444-7452 doi:10.1103/PhysRevB.32.7444 (1985) |
| [17] | Levine, D., Lubensky, T.C., Ostlund, S., Ramaswamy, S., Steinhardt, P.J., & Toner, J Elasticity and dislocations in pentagonal and icosahedral quasicrystals. Physical Review Letters, 54(14), 1520-1523 doi:10.1103/PhysRevLett.54.1520 (1985) |
| [18] | Lubensky, T.C Symmetry, elasticity and hydrodynamics in quasiperiodic. Introduction to Quasicrystals, Academic Press, San Diego, 199-273 (1988) |
| [19] | Socolar, J.E., Lubensky, T.C., & Steinhardt, P.J Phonons, phasons, and dislocations in quasicrystals. Physical Review B, 34(5), 3345-3360 doi:10.1103/PhysRevB.34.3345 (1986) |
| [20] | Rochal, S.B., & Lorman, V.L Minimal model of the phonon-phason dynamics in icosahedral quasicrystals and its application to the problem of internal friction in the i-AlPdMn alloy. Physical Review B, 66(14), 144204 doi:10.1103/PhysRevB.66.144204 (2002) |
| [21] | Fan, T.Y., Wang, X.F., Li, W., & Zhu, A.Y Elasto-hydrodynamics of quasicrystals. Philosophical Magazine, 89(6), 501-512 doi:10.1080/14786430802562157 (2009) |
| [22] | Zhu, A.Y., & Fan, T.Y Dynamic crack propagation in decagonal Al-Ni-Co quasicrystal. Journal of Physics:Condensed Matter, 20(29), 20(29), 295217 doi:10.1088/0953-8984/20/29/295217 (2008) |
| [23] | Ding, D.H., Yang, W., Hu, C., & Wang, R. Generalized elasticity theory of quasicrystals. Physical Review B, 48(10), 7003-7010 doi:10.1103/PhysRevB.48.7003 (1993) |
| [24] | Hu, C., Wang, R., & Ding, D.H Symmetry groups, physical property tensors, elasticity and dislocations in quasicrystals. Reports on Progress in Physics, 63(1), 1-39 doi:10.1088/0034-4885/63/1/201 (2000) |
| [25] | Fan, T.Y Mathematical Theory of Elasticity of Quasicrystals and Its Applications. Springer, Beijing (2011) |
| [26] | Dzyaloshinskii, I.E., & Volovick, G.E Poisson brackets in condensed matter physics. Annals of Physics, 125(1), 67-97 doi:10.1016/0003-4916(80)90119-0 (1980) |
| [27] | Fan, T.Y Poisson bracket method and its applications to quasicrystals, liquid crystals and a class of soft matter (in Chinese). Chinese Journal of Theoretical and Applied Mechanics, 45(4), 548-559 (2013) |
| [28] | Jeong, H.C., & Steinhardt, P.J Finite-temperature elasticity phase transition in decagonal quasicrystals. Physical Review B, 48(13), 9394-9403 doi:10.1103/PhysRevB.48.9394 (1993) |
| [29] | Guo, L.H., & Fan, T.Y Solvability on boundary-value problems of elasticity of three-dimensional quasicrystals. Applied Mathematics and Mechanics (English Edition), 28(8), 1061-1070 (2007) |
 2016, Vol. 37
2016, Vol. 37










