1 Introduction

Over the past two decades, the lattice Boltzmann equation (LBE)^[1-2] has attracted considerable attention as an available alternative originated from lattice gas automata for solving academic problems in computational fluid dynamics and preliminary applications in engineering. The LBE, as an efficient and effective simulation tool, has been successfully proven in multiphase flows^[3-4], complex flows^[5-6], turbulent flows^[7-8] for incompressible flows. Unlike the macroscopic Navier-Stokes equations, the LBE is a mesoscopic approach based on the kinetic theory of fluids. The macroscopic density, velocity and other physical quantities can be obtained with the help of particle distribution functions^[9]. So the LBE contains the following inherent features. Firstly, the linear streaming and collision processes of fictitious particles in the LBE solver cannot effectively simulate the nonlinear convection and diffusion effects on the macroscopic state. Besides, the LBE involves the problems of solution of the differential equation as algebraic formulations. Nevertheless, the standard LBE is limited to the simple geometric configuration and uniform Cartesian mesh due to the lattice uniformity. And there is a tie-up between the time interval and mesh spacing.

In order to overcome LBE's shortcomings and retain its merits, Shu et al.^[10] proposed a lattice Boltzmann flux solver (LBFS) for simulating incompressible flows based on single-relaxation-time. The LBFS has achieved fast development and widespread application. Both Wang et al.^[11] and Cao^[12] developed the thermal LBFS on the basis of LBFS, and the solvers have been validated to solve thermal flow problems effectively and flexibly. Wang et al.^[13] applied the LBFS into the field of multiphase flows. Inspired by the research of LBFS and in consideration of accuracy and stability of multiple-relaxation-time (MRT) scheme in numerical simulations^[14-16], the MRT-LBFS is proposed in the present work. The MRT scheme can radically remove the constraints of the fixed Prandtl number and the ratio between the kinematic and bulk viscosities. And the scheme owns the ability to simulate the higher Reynolds number flows^[17-19]. The MRT-LBFS uses the finite volume method to discretize Navier-Stokes equations so that the flow variables at the cell center are obtained by marching in time, and the interface fluxes are evaluated by local reconstruction of LBE solution with the help of Chapman-Enskog analysis.

The boundary condition plays an essential role due to its effects of numerical stability and accuracy in computational fluid dynamics. Usually, the body-fitted mesh is used to simulate the flow around an arbitrary body. And in the meantime, it involves the complicated processes including coordinate transformation and mesh generation. In order to simplify the process, the immersed boundary method (IBM) is applied so that the non-body conforming Cartesian grid can be used. The flow field is represented by Eulerian mesh, and the solid boundary of immersed body is represented by Lagrangian points. The basic idea of the IBM is to treat the physical boundary as a singular force in the Navier-Stokes equations rather than by a real body. The IBM mainly divides into two groups based on the forcing function^[20], namely continuous forcing and discrete (or direct) forcing. Peskin^[21] firstly proposed the IBM for simulating flow patterns around heart valves using continuous force in 1972. The direct forcing method^[22] is suitable for simulation of flows with higher Reynolds numbers. However, the above methods cannot satisfy the no-slip boundary condition. So the boundary condition-enforced IBM, which was proposed by Wu and Shu^[23-24], is adopted due to the accuracy for the satisfaction no-slip boundary condition in this work. In this IBM, the unknown restoring force is calculated by enforcing the no-slip boundary condition. As a consequence, the streamlines penetration of the solid body can be avoided, and more accurate numerical results can be obtained. Wang et al.^[25] simulated fluid-structure interaction problems by combining the boundary condition-enforced IBM and LBFS. Qiu et al.^[26] used boundary condition-enforced IBM to simulate the compressible viscous flows. Ren et al.^[27] used the boundary condition-enforced IBM for simulations of free and forced convection problems with the Dirichlet-type boundary condition. However, unlike the direct forcing method, this IBM has not been expanded to simulate turbulent flows so far. Therefore, it is a challenge to solve turbulent flows for the boundary condition-enforced immersed boundary method in the future research.

From the above analysis, we attempt to implement a newly developed method called the immersed boundary-MRT lattice Boltzmann flux solver (IB-MRT-LBFS) in this paper. In order to validate the accuracy of this method, flows past circular and elliptic cylinders are simulated firstly. Then, the flow characteristics of flows past elliptic cylinders at different Reynolds numbers and axis ratios are further studied. Additionally, the NACA0012 airfoil, as the complex geometry, is simulated at the Reynolds number 500. As an efficient method for simulating incompressible flows on non-uniform Cartesian-staggered grids, the IB-MRT-LBFS avoids a number of works about mesh generation for engineers and provides an effective, flexible and simple pathway to deal with complex structure problems.

2 Governing equations and numerical method 2.1 Navier-Stokes equations, LBE and Chapman-Enskog expansion analysis

As a bridge, the multi-scale Chapman-Enskog expansion analysis is able to build a relationship between the Navier-Stokes equations and the LBE in the low Mach number limit. Therefore, the variables and fluxes in the macroscopic equations can be obtained by density distribution functions in the LBE solution.

2.1.1 Navier-Stokes equations

For incompressible viscous fluids, the macroscopic Navier-Stokes equations can be written as follows:

(1)

(2)

where ρ, u, p and µ represent the fluid density, the velocity, the pressure and the dynamic viscosity coefficient, respectively.

2.1.2 LBE

The LBE with the MRT based on the BGK approximation can be written as follows:

(3)

where e_α is the particle velocity in the α direction; r represents the physical location, δt is the streaming time step; M is the transformation matrix from the particle velocity space f_α and f_α^eq to the moment space m_α and m_α^eq with the relations of m_α = Mf_α and m_α^eq = Mf_α^eq; f_α and f_α^eq are the discrete density distribution function and its corresponding equilibrium term; S = diag(s₀, s₁, s₂, s₃, s₄, s₅, s₆, s₇, s₈) is a diagonal matrix, where s₀=s₃=s₅ can be set at 0 to reduce the computational cost because of the mass and momentum conservation during the collision process. s₇=s₈= 1/τ. The relaxation parameter can be obtained by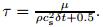

For the two-dimensional (2D) case, the most popular lattice velocity model is the D2Q9 model which is shown in Fig. 1, and the velocity is given by

(4)

where c = δ_x/δ_t, δ_x and δ_t are the lattice intervals in space and time step. The corresponding equilibrium density distribution function, the LBGK model, is

(5)

with

is the sound speed of the model.

Once the density distribution functions at the physical location r are obtained, the macroscopic density ρ and momentum ρu are computed by

(6)

2.1.3 Chapman-Enskog expansion analysis

By the multi-scale Chapman-Enskog expansion, the density distribution function, the temporal derivative, and the spatial derivative can be expanded as, respectively,

(7)

(8)

(9)

(10)

where ε is a small parameter proportional to the Knudsen number. By performing a Taylor series expansion in time and space on (3), the following equations are obtained:

(11)

(12)

(13)

By taking the zeroth-and first-moment summations of (12) and (13) over α and combining the resultant formulations on the t₀ and t₁ time scales, respectively, the following equations can be derived:

(14)

(15)

where

(16)

It can be seen that (14)-(15) recover the Navier-Stokes equations (1)-(2) to the first order of ε. Define m_α^neq as the density distribution function non-equilibrium term in the moment space, and it can be approximated by

(17)

Therefore, (16) can be expressed as

(18)

2.2 IB-MRT LBFs

For incompressible viscous fluids, the macroscopic Navier-Stokes equations based on IBM can be written as

(19)

(20)

where F stands for a restoring force given by the IBM.

According to the relationships, which is established in Section 2.1 between the fluxes in Navier-Stokes equations and the density distribution functions in the lattice Boltzmann method, the governing equations, based on the IB-MRT-LBFS, can be expressed as follows:

(21)

(22)

where

(23)

(24)

The new numerical method decouples the solution of governing equations in two steps: the predictor step and the corrector step. The MRT-LBFS is implemented in the predictor step, and the boundary condition-enforced IBM is applied in the corrector step.

(ⅰ) Predict the flow field variables ρⁿ⁺¹ and u^* without taking account of boundary function,

(25)

(26)

(ⅱ) Correct the velocity of the flow field in order to accurately satisfy the no-slip boundary condition. Define the velocity after correction as uⁿ⁺¹, and the expression of restoring force can be written as

(27)

Then, the details of two steps will be presented below.

2.2.1 LBFs

The discrete term of the governing equations (25)-(26) with the finite volume method is

(28)

where W = (ρ, ρu)^T. dV_i and dS_k are the volume of ith control volume and the area of the kth interface; n is the unit outward normal vector on the kth interface.

The detailed expression for the interface fluxes depends on different lattice velocity models. For numerical simulations in this paper, the D2Q9 lattice velocity model is used, and in this situation the fluxes can be written in detail as follows:

(29)

where

(30)

Thus, the fluxes can be obtained by solving the equilibrium and non-equilibrium density distribution function. By using Taylor series expansion, the below expression can be derived,

(31)

From (31) and (24), the expression can be obtained,

(32)

Thus, the fluxes can be calculated by solving the equilibrium distribution function m_α^eq(r-e_αδ_t, t -δ_t) and m_α^eq(r, t).

The flow properties of eight vertexes of the D2Q9 model can be evaluated by interpolation with the given flow properties at the cell centers of two adjacent control volumes shown in Fig. 2. We assume that the physical locations for the two cell centers and their interface are r_i, r_i+1, and r, respectively.

The interpolation formulation, which is used to calculate the flow properties of the interface surrounding points, can be given as

(33)

where ψ stands for ρ and u.

After computing ψ(r − e_αδ_t, t − δ_t) by (33), f_α^eq(r − e_αδ_t, t − δ_t) can be obtained according to (5). Then, m_α^eq(r − e_αδ_t, t − δ_t) can be computed by

According to for the D2Q9 model, m_α^eq(r, t) can be computed from the flow properties at the position r. The reconstructed flow variables at the interface by the LBE solutions are as follows:

(34)

(35)

Then, the fluxes R_k can be calculated by (29) after obtaining m_α^eq(r − e_αδ_t, t − δ_t) and m_α^eq(r, t).

2.2.2 Boundary condition-enforced IBM

After obtaining the intermediate velocity u^*, we will perform velocity correction, which is performed by applying boundary condition-enforced IBM. The key point is to ensure no-slip boundary conditions. Figure 3 shows a solid boundary immersed in a 2D computational domain.

If we define the velocity after correction as uⁿ⁺¹, the expression is shown as

(36)

and the velocity correction ∆u at the Eulerian point can be obtained by the following Dirac delta function through interpolation:

(37)

where D is a continuous kernel function given by

(38)

(39)

To guarantee the no-slip boundary conditions, the velocities of the Lagrangian points must be identical to those fluid velocities at the same positions. The fluid velocities can be obtained through interpolations of the corrected velocities of the Eulerian points,

(40)

where h is the grid size of Eulerian mesh, N and M are the numbers of Lagrangian points and Eulerian points. (18) and (19) are substituted into (22), then

(41)

The above equation can be rewritten in a matrix form,

(42)

where

(43a)

(43b)

(43c)

The linear system of (42) is solved by a direct method so that the unknowns at all Lagrangian points can be obtained simultaneously. Then, the velocity correction ∆u at the Eulerian point can be obtained by (37), and the flow velocity uⁿ⁺¹ can be solved by (36).

2.3 Computational sequence

The complete numerical simulation procedures for each time step of the proposed IB-MRTLBFS method are summarized in Fig. 4.

3 Numerical validations

In this section, in order to validate the proposed flux solver, several numerical simulation tests are conducted. At first, flows past a stationary circular cylinder of different Reynolds numbers are simulated. Next, more elliptic cylinders of different Reynolds numbers and axis ratios are simulated for laminar fluid flow in order to analyze the effects of axis ratios on the drag coefficient and Stroutal number. Finally, the flow past an NACA0012 airfoil is simulated so that the accuracy of the method is further validated to calculate incompressible flows past more complicated geometries.

The force coefficients and the Strouhal number are defined as follows:

(44)

(45)

(46)

where f_x is the x component of force density f, and f_y is the y component of force density f. f is the dimensionless frequency.

3.1 Flow past circular cylinder

In the present simulations, steady (Re=20 and 40) flows and unsteady (Re=100 and 200) flows past a stationary circular cylinder are studied here. The flow and geometrical parameters are set as ρ = 1.0, U_∞=0.1, and D=1.0. The schematic diagram of computational domain and boundary conditions is shown in Fig. 5. For all cases of numerical validations, the Dirichlet boundary condition is used on the inlet boundary as u_x = U_∞ and u_y = 0, the outlet boundary condition is as and , and the top and bottom boundary conditions are both as and u_y=0. The no-slip boundary of the cylinder surface is represented by 150 Lagrangian points with the uniform distribution. The computational mesh, which is shown in Fig. 6, is with non-uniform mesh of 385×408, and the cylinder is placed in a square region with a uniform mesh of 120×120.

Firstly, this numerical method is validated by simulation of the steady flow. The present results which are shown in Table 1, including drag coefficients and recirculation lengths, are compared with results in the literature, and good agreement is achieved. Figure 7 shows the streamlines, and it can be clearly seen that two symmetric reverse vortexes appear. And there are no penetration streamlines around the solid boundary so that it illustrates that the immersed boundary technique satisfies the no-slip boundary condition. Then, this method is validated by simulating the unsteady flow. Figure 8 shows the time evolution of drag and lift coefficients for unsteady flow, and they show periodic feature, and the period of the lift coefficient is twice of that of drag coefficient. Force coefficients and Strouhal number obtained by the present method are compared with previous 2D computational results in Table 2, and good agreement is achieved.

From Table 1 and Table 2, the present results are compared with the simulation results by the IB-SRT-LBFS (Wang et al.^[25]). It illustrates that there is no obvious difference between the IB-MRT-LBFS and IB-SRT-LBFS in terms of accuracy. In addition, the flow past a stationary circular cylinder (Re=20) is also simulated to compare the stability and efficiency between IB-MRT-LBFS and IB-SRT-LBFS. For that case, IB-MRT-LBFS is more stable than IB-SRT-LBFS when the time step is increased or the mesh is reduced. From Table 3, it can be seen clearly that IB-MRT-LBFS needs a little more iteration numbers and run time than the IB-SRT-LBFS at the same time step to satisfy the convergence criterion. Due to the stability of IB-MRT-LBFS, the time step can be appropriately increased. For this validation case, the calculation can be achieved by IB-MRT-LBFS when the time step is equal to 0.005, but the calculation does not converge by the IB-SRT-LBFS. It is also demonstrated that the computational time can be shortened for the IB-MRT-LBFS by increasing the time step from Table 3.

3.2 Flow past elliptic cylinder

Besides circular cross sections, many engineering applications involve flows over cylinders of various cross sections, rectangular and elliptic, such as electronic cooling systems, heat exchangers, solar energy systems, chemical process^[33-36]. An elliptic cylinder in general form becomes a flat plate and also a circular cylinder depending on different axis ratio (A_R = a/b) between major and minor axis. Then, in the next simulations, more flows past elliptic cylinders with different axis ratios and Reynolds numbers are simulated. The effects of axis ratio and Reynolds number on the drag force and Stroutal number are analyzed. The computational domain (see Fig. 9) and the flow parameters are set as the same as that of flow past a circular cylinder. The numerical simulation cases are carried out for aspect ratios ranging from 0.25 to 1.00 and for Reynolds numbers ranging from 50 to 200.

For elliptical cylinders (A_R < 1.0), the pressure drag is greater than that of a circular cylinder since it acts normal to the surface while the viscous drag is smaller due to the tangent vector of force. From Fig. 10(a), it can be seen that the drag coefficient is decreasing as A_R increases for a given Reynolds number, and general increases as the Reynolds number increases for elliptic cylinders. However, the drag coefficient shows the slow descending tendency at A_R=1.00 and Re>100. Because of symmetrical structure of circular cylinder, the pressure drag will be cancelled out so the total drag reaches the minimum value. Figure 10(b) shows the evolution of Strouhal number with increasing Reynolds number for different aspect ratios. For A_R=0.25 and 0.5, the Strouhal number is increasing at the beginning till Re=125 and 100, respectively. Then, it declines by the incremental Reynolds number. For A_R=0.75 and 1.00, the Strouhal number is gradually soared till Reynolds number equal to 200.

3.3 Flow past NACA0012 airfoil

Flow past an NACA0012 airfoil is selected to further validate the present method. Figure 11 shows an NACA-0012 wing cross section as the same in Ref. [38]. The Reynolds number is equal to 500, and the angle of attack is chosen as α = 0°. The computational domain is L_x × L_y = 40 × 40 in units of chord length. The free stream condition is given by the density ρ = 1.0 and the Mach number Ma = 0.2. Natural boundary conditions are applied on the upper, lower and outlet boundaries. The computational mesh is shown in Fig. 12, including the whole computational mesh and detail view. The airfoil surface is represented by 300 Lagrangian points with the uniform distribution, and it is located in the rectangle region with a uniform mesh of 260×60. The whole computational mesh is with the non-uniform mesh of 520×320.

Pressure distribution along the surface of NACA0012 at Re=500, α=0° is shown in Fig. 13 and the drag and lift coefficients are shown in Table 4 which are computed by the IB-MRT-LBFS. The results are compared with the numerical simulation results by other solvers, including CFL3D, power flow and GILBM. It illustrates that the present solutions are very trustworthy. Velocity profiles of NACA0012 at x/c=0.0, 0.25, 0.5, 0.75, 1.0, and comparison with the results by power flow and CFL3D are shown in Fig. 14. The results are extremely close to CFL3D results. It declares the accuracy in velocity distribution of IB-MRT-LBFS.

4 Conclusions

The IB-MRT-LBFS is presented for the numerical simulations of incompressible flows. Based on the finite volume method, the new developed method is combining the IBM with LBFS (MRT type) to use simple Cartesian mesh for simulation of flow past complex geometries in laminar flow. The interface fluxes are evaluated by local reconstruction of the lattice Boltzmann model (D2Q9). For the purpose of no-slip boundary condition, the intermediate velocity is corrected by the boundary condition-enforced immersed boundary method. Flow past a circular and an elliptic cylinder are simulated in order to verify the method suitable for simulating laminar flows on Cartesian meshes. And for the validation of the ability of IB-MRT-LBFS to simulate the flow over more complex geometry, NACA0012 airfoil is simulated by this method. The present numerical results are in good agreement with the available data in the literature, which demonstrates the excellent capability of the present scheme in simulating laminar flows. In the future work, the extension of the present method is to high Reynolds number flows and moving boundary problems.