Nomenclature
a,	radius of inner sphere;	υϕ,	micro-rotation component;
b,	radius of outer sphere;	ψ,	stream function;
μ,	dynamic viscosity;	D,	drag force;
κ,	vertex viscosity;	W,	wall correction factor;
ω,	microrotation vector;	Q,	flow rate;
α, β, γ,	gyro viscosity coefficient;	,	modified Bessel functions;
p,	pressure;	,	Gegenbauer functions.

1 Introduction

Eringen^[1] introduced the theory of a micro-polar fluid. Ramkisoon and Majumdar^[2] evaluated drag on an axially symmetric body in a Stokes flow of a micropolar fluid and observed that the drag in the micro-polar fluid is greater than that of the classical fluid. Rao and Rao^[3] studied the problem of a slow stationary flow of a micro-polar fluid past a sphere. Sawada et al.^[4] studied the problem of Stokesian flow of micro-polar fluid past a sphere. Ramkissoon^[5] solved the problem of the flow of micro-polar fluid past a Newtonian fluid sphere. Creeping flows of micro-polar fluids past a porous sphere were solved by Srinivasacharya and Rajyalakshmi^[6]. Saad^[7] studied cell models for micro-polar flows past a viscous fluid sphere using Happel, Kuwabara, Cunningham and Kvashnin cell models and obtained the drag force acting on the sphere. Axisymmetric creeping flows of micro-polar fluids over a sphere coated with a thin fluid film were studied by Gupta and Deo^[8].

Leonov^[9] solved the problem of the slow stationary flow of viscous fluid about a permeable sphere by taking the small thickness of the permeable surface and determined the resistance exerted by the fluid on the sphere. Nandakumar and Masliyah^[10] solved the problem of laminar flows past a permeable sphere using the Navier-Stokes equation outside the sphere and Brinkman's equation inside the sphere, and observed that the computed drag factors are 10% smaller than the experimental value observed by Masliyah and Polikar^[11]. Wolfersdorf^[12] solved the problem of creeping flow past a permeable sphere and past a permeable sphere containing a concentric impermeable sphere for the Newtonian fluid by using the Darcy law and no-slip condition at the surface of the sphere, and obtained that the drag on the permeable sphere is smaller than that of a rigid sphere. Padmavati et al.^[13] solved the problem of Stokes flow past a sphere with the permeable surface for a non-axisymmetric case, gave a general method for calculating non-axisymmetric flows both outside and inside the permeable spherical boundary, and found the expression for the drag and torque on the sphere using representation for the pressure and velocity following Palaniappan et al.^[14]. The slow viscous fluid past a spinning sphere with the permeable surface was studied by Vasudeviah and Malathi^[15], and derived the expression for the drag coefficient on the body which can be used as a formula for the determination of the permeability of the sphere. Murthy et al.^[16] studied the problem of uniform flows of incompressible couple stress fluids past a permeable sphere. Aparna and Murthy^[17] solved the problem of the uniform flow of incompressible micro-polar fluid past a permeable sphere. Mishra and Gupta^[18] solved the problem of drag on a permeable sphere placed in the micro-polar fluid with the non-zero boundary condition for micro-rotation, and observed that drag is greater in the case of zero micro-rotation vector than the case of non-zero micro-rotation vector. The problem of the motion of a particle when it passes the center of a spherical container serves as a model of interaction in multi-particle systems. This class of problems is important because it provides some information on wall effects. A number of researchers have considered the creeping motion of the rigid or fluid sphere in a spherical container. Cunningham^[19] and Williams^[20], independently, considered the motion of a solid sphere in a spherical container. Wall effects for rigid and fluid spheres in slow motion with a moving liquid were studied by Haberman and Sayre^[21]. Usha^[22] solved the problem of creeping flow with concentric permeable spheres in relative motion for the Newtonian fluid and calculated the drag force and wall correction factor. Srinivasacharya^[23] studied motion of the porous sphere in a spherical container by using Brinkman's model for the flow inside the porous sphere and the Stokes equation for the flow in the spherical container, and they calculated the drag force experienced by the porous spherical particle and the wall correction factor. Ramkissoon and Rahaman^[24] solved the problem of non-Newtonian (Riener-Rivlin) fluid sphere in a spherical container and evaluated the drag experienced by the inner sphere and wall correction factor, and then they solved wall effects on a solid spherical particle contained in a spheroidal container using the no-slip condition^[25]. Creeping motions of a composite sphere in a concentric spherical cavity for the Newtonian fluid were studied by Keh and Chou^[26]. Srinivasacharya and Prasad^[27] studied the motion of a porous spherical shell in a bounded medium, and they observed that the wall correction factor increased as the separation parameter increased. Wall effects on the Reiner-Rivlin liquid spheroid were studied by Jaiswal and Gupta^[28], who also studied the problem of creeping flow over a liquid core composed of a porous cell for the non-Newtonian fluid^[29]. The problem of quasisteady translation and steady rotation of a porous sphere in a spherical container was studied by Saad^[30] using the stress jump condition. Jaiswal^[31] solved the problem of viscous stream over the Reiner-Rivlin fluid sphere in a deformed spherical vessel and evaluated the drag force.

This paper concerns the motion of a permeable spherical shell in a spherical container filled with the non-Newtonian (micro-polar fluid) fluid. We assume that the Reynolds number is sufficiently small so that the inertial terms can be neglected in comparison with viscous terms in the fluid momentum equation. Mathematical equations of the flow fields are obtained in terms of the stream function. Drag experienced by the permeable sphere, the wall correction factor, and the flow rate through the permeable surface are obtained for the frictionless impermeable spherical container and the zero shear stress at the impermeable spherical container, and their variations with respect to various fluid parameters are presented.

2 Mathematical formulation of problem

In the present mathematical model, we consider a permeable sphere of the radius a moving with the constant velocity U in the positive z-direction in a big spherical container of the radius b which is filled with the micro-polar fluid (see Fig. 1). This is equivalent to the inner sphere at rest while the outer sphere moves with the constant velocity U in the negative z-direction. We consider that the thickness of the permeable sphere is smaller than a and b. The regions a≤R≤ b and R≤ a are denoted as Regions Ⅰ and Ⅱ, respectively.

Under the Stokes approximation in the absence of body force and body couple, the governing equations for the slow steady motion of micro-polar fluid can be written as

(1)

(2)

(3)

where are the velocity vector, pressure, and micro-rotation vector, μ is the dynamics viscosity coefficient of the fluid, κ is the vortex viscosity coefficient, and α, β, γ are the gyro viscosity coefficients satisfying the following inequalities:

(4)

The constitutive equation for the isotropic non-Newtonian micro-polar fluid is given by

(5)

where is the rate of strain, is the stress tensor, is the Kronecker delta, is the vorticity vector, and is the component of micro-rotation vector. Since the flow of the fluid is axially symmetric, all the physical quantities are independent of ϕ. Therefore, we can introduce the stream function which is related to the velocity in the spherical coordinate system by Happel and Brenner^[32],

(6)

where are the unit vectors along R-, θ-, ϕ-directions, and we find two velocity components of the flow as

(7)

In order to non-dimensionalize the equations and variables, we put

(8)

Eliminating the pressure from Eq. (2) and using Eq. (3), we get the differential equation,

(9)

where and the micro-polar parameter

(10)

Solving Eq. (3), we obtain the micro-rotation component,

(11)

In the dimensional form, the expressions of the normal and tangential stresses in the axisymmetric spherical coordinate, respectively, are given by

Using Eqs. (2) and (3), we calculate the pressure distributions for Regions Ⅰ and Ⅱ as follows:

(12)

(13)

3 Boundary conditions

We use the boundary conditions which are physically realistic and mathematically consistent for the proposed problem. The parameters pertaining to Regions Ⅰ and Ⅱ of the fluid are distinguished by the index in the superscript under the bracket of an entity , i=1, 2, respectively.

3.1 At permeable surface r=1

The boundary conditions at the permeable surface are no-slip boundary conditions for the tangential component of the velocity and zero-micro-rotation components, the normal velocity v_r is continuous and equal to the filtration velocity V(θ) with the negative sign, the filtration velocity V(θ) is proportional to the difference of the hydrodynamic pressure,

(14)

(15)

(16)

(17)

where k is the permeability coefficient, k> 0.

3.2 At outer surface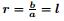

At the outer surface, we assume that the micro-rotation component is zero, and the fluid streams with the uniform velocity U, i.e.,

(18)

(19)

In addition to the above boundary conditions, we need one more condition to solve the boundary value problem

(ⅰ) Frictionless impermeable spherical container

The tangential velocity v_θ =Usin θ implies

(20)

(ⅱ) Zero shear stress at impermeable spherical container

The tangential stress vanishes at the impermeable spherical

(21)

4 Solution of problem and determination of arbitrary constants

Applying the method of separation of variable, we get the general solution to Eq. (9),

(22)

where are modified Bessel functions, and G_n(ζ) and H_n(ζ) are Gegenbauer functions of the first and second kinds, respectively. We ignore the terms which are multiplied by G₀(ζ), G₁(ζ), and H_n(ζ) (for all n) due to irregularity of G₀ (ζ), G₁(ζ), and H_n(ζ) at the symmetry z-axis. In case of perfect sphere, the stream function solution contains only the terms of the order n=2 of the general solution (22). Hence, if ψ⁽¹⁾ denotes the stream function for Regions Ⅰ, then the stream function solution for the flow field of Regions Ⅰ

the terms involving create singularity at the origin. Therefore, we neglect these terms from the solution (22) for Region Ⅱ. If ψ⁽²⁾ denotes the stream function for the internal flow r≤ a, then the stream function solution for the flow of Regions Ⅱ

The micro-rotation components υ_ϕ⁽¹⁾ and υ_ϕ⁽²⁾ for Regions Ⅰ and Ⅱ are

Substituting the values of stream functions and micro-rotation components into boundary conditions from (14) to (21), we obtain the following linear equations.

4.1 At permeable surface r=1 4.2 At outer surface

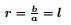
(ⅰ) Frictionless impermeable spherical container

(ⅱ) Zero shear stress at impermeable spherical container

Unknown constants A₂', B₂', C₂', A₂, B₂, C₂, D₂, E₂, and F₂ are determined by using the above linear equations given in Subsections 4.1 and 4.2. The values of these constants are very large. Therefore, we have not written in this paper.

5 Evaluation of drag force, wall correction factor, and rate of flow 5.1 Drag force

The drag experienced by the permeable sphere is evaluated using the simple elegant formula,

(23)

where T_rr and T_rθ are the normal and tangential stress components, respectively. Substituting the values of T_rr and T_rθ into Eq. (23), we obtain the drag force,

(24)

The non-dimensional drag coefficient can be defined as

For the Newtonian liquid (κ =0) surrounding a permeable sphere of the radius a that contains in a spherical region of the radius b, we have the following expressions for the hydrodynamic drag force.

(ⅰ) Frictionless impermeable spherical container

which agrees with that in Ref.[22].

(ⅱ) Zero shear stress at impermeable spherical container

which also agrees with that in Ref.[22].

5.2 Wall correction factor W

The wall correction factor is defined as

(25)

where

(26)

(ⅰ) Frictionless impermeable spherical container

(a) For the Newtonian fluid κ =0, the wall correction factor is

which is the wall correction factor for the motion of a permeable sphere in a spherical region filled with the Newtonian fluid obtained by Usha^[22].

(b) Putting κ =0 and k=0 into Eq. (25), we obtain

which is the wall correction factor given by Happel and Brenner^[33] for the case of motion of impermeable sphere contained in a rigid sphere.

(ⅱ) Zero shear stress at impermeable spherical container

(a) Putting κ =0 into Eq. (25), we obtain

which is the wall correction factor obtained by Usha^[22] in the study of creeping motion of a permeable sphere at the center of a stress free impermeable sphere.

(b) Putting κ =0 and k=0 in Eq. (25), we obtain

which is a well known result previously obtained by Happel and Brenner^[33] in the study of creeping motion of the rigid sphere at the center of an outer stress free spherical envelope.

5.3 Flow rate

The flow rate through the permeable surface is given by Happel and Brenner^[33],

where S₁ is the front half of the sphere between 0≤ θ ≤ π/2, and v · n is the normal component of the velocity.

Hence, the dimensionless flow rate through the permeable sphere is given by

6 Results and discussion

D_N and D_N^* represent the non-dimensional drags for the frictionless and stress free impermeable spherical container, respectively. The variation of the non-dimensional drag for both conditions (20) and (21) with respect to the permeability parameter k for the fixed values of κ =10, λ =5, μ =10, and l=1.6 is shown in Fig. 2. It is observed from Fig. 2 that, as the permeability parameter increases, the drag force experienced by the permeable sphere decreases. In the interval (0, 2) of the permeability parameter, the drag decreases rapidly, afterwards it becomes steady. It is noticed that the drag is maximum when permeability of the inner sphere is zero (k=0); physically, it means that, the impermeable sphere experiences more drag than the permeable sphere. Also, it is clear from Fig. 2 that the drag force is greater for the frictionless impermeable spherical container than the zero shear stress at the impermeable spherical container. Figure 3 shows the variation of the drag coefficient with respect to the ratio of the radius of the outer and inner spheres for the fixed values of κ =10, λ =5, μ =10, and l=1.6. Figure 3 reveals that the drag force decreases monotonically for the condition (20) as the radius of outer sphere increases. However, for the zero stress condition, the drag increases in the interval 1≤ l≤ 1.5, and afterwards it decreases. The effect of vertex viscosity κ on the drag force for both conditions (20) and (21) for the fixed values of l=1.5, λ =5, μ =10, and k=1.6 is shown in Fig. 4. It is observed for both conditions that the drag force increases monotonically with increasing κ. It is interesting to note that the drag is greater in the case of the condition (20) than the case of the condition (21). κ =0 represents the result for the Newtonian fluid past a permeable sphere contained in a spherical region. Physically, it implies that the drag is minimum for the Newtonian fluid than that for the micro-polar fluid.

W_C and W_C^* signify the wall correction factors for the frictionless and stress free impermeable spherical container, respectively. Variations of the wall correction factor versus the permeability parameter for the fixed values of l=2.3, κ =5, λ =10, and μ =5 are shown in Fig. 5. It is observed from Fig. 5 that the behavior of the wall correction factor with the permeability parameter is similar to the variation of the drag force versus the permeability parameter. Figure 6 shows the variation of the wall correction factor for the two conditions (20) and (21) with respect to the dynamic viscosity μ for the fixed values of k=1.3, κ =5, λ =10, and l=1.6. It is noticed from this figure that the wall correction factor decreases rapidly when 0≤ μ ≤ 20, and then it decreases gradually. Figure 7 depicts the effect of vertex viscosity κ on the wall correction factor for the fixed values of k=1.3, μ =5, λ =10, and l=1.6. It divulges that the wall correction factor increases as κ increases. Figure 8 represents the variation of the wall correction factor for the frictionless impermeable spherical container versus the ratio of the radius of the spheres l for various values of the permeability parameter k and fixed values of κ =0.3, λ =5, and μ =10. Figure 8 reveals that, as the outer sphere gets larger, the wall correction factor decreases. It is also observed from Fig. 8 that the wall correction factor decreases sharply in the initial stage and then it decreases slowly. It is noticed that the W_C is greater for the impermeable sphere.

The variation of the flow rate through the permeable surface for both conditions (20) and (21) with respect to the permeability parameter k for the fixed values of λ =5, l=1.6, μ =5, and κ =10 is shown in Fig. 9. We denote the flow rate for the frictionless and stress free impermeable spherical containers by Q_N and Q_N^*, respectively. We can see that the flow rate is increasing sharply when 0≤ k≤ 1.8 and then it becomes almost constant for the very permeable sphere. Physically, it implies that the flow rate through the permeable sphere is not very much influenced for the extremely permeable surface. We observe from Fig. 9 that, for the impermeable sphere (k=0), the flow rate is minimum. Figure 10 is the variation of the flow rate versus the ratio of the radius of the spheres for the fixed values of k=0.8, κ =5, μ =10, and λ =10. It can be seen from Fig. 10 that the flow rate decreases as the outer sphere gets larger. Figure 11 is the variation of the flow rate with respect to the dynamic viscosity μ for the fixed values of k=1.2, l=1.6, κ =5, and λ =5. It is clear from this figure that there is a slight decrease in the flow rate as μ is increasing. It is observed that Q_N is greater than Q_N^* in each case.

7 Conclusions

The problem of the motion of a permeable shell in a spherical container filled with a micro-polar fluid is solved. Analytical solutions for the flow fields are obtained in terms of modified Bessel functions and Gegenbauer functions. The pressures, micro-rotation components, flow rate through the permeable surface, the drag force experienced by the permeable spheres, the wall correction factor are calculated for the frictionless impermeable spherical container and the zero shear stress at the impermeable spherical container. The variations of the drag force, the wall corrector factor and the flow rate with respect to different fluid parameters are discussed and presented in the graphical form for both cases. It is observed that the impermeable sphere experiences more drag than the permeable sphere. The drag force, the wall correction factor, and the flow rate are greater for the frictionless impermeable spherical container than the zero shear stress at the impermeable spherical container. It is also observed that the flow rate is decreasing as the outer sphere gets larger.