1 Introduction

At micro/nano scales, highly curved structures widely exist, and the importance of curved space form is gradually realized.Previously, we discussed the interaction between curved spaces(i.e., curved surface and curved line) and particles^[1-4]. Then, the interaction between curved surface bodies and particles was explored^[5-6]. As a three-dimensional body, the curved surface body belongs to the flat Euclid space. However, at small scales, the surface of the body is highly curved, and most of the particles are distributed on the surface with large specific surface area. From this viewpoint, the highly curved surface body is closely related to the curved space^[5].

In the previous paper^[6], the interaction between a curved surface body and a particle was classified into three basic modes.The first one is the interaction between a curved surface body and a particle located outside the body (see Fig. 1(a)), which is marked as Mode 1. The second one is the interaction between a curved surface body and a particle located on the surface of the body (see Fig. 1(b)) and is marked as Mode 2. The third one is the interaction between a curved surface body and a particle located inside the body (see Fig. 1(c)), which is called Mode 3. Modes 1and 2 have been well studied^[6-7]. Based on the negative exponential pair potential ((1/R)ⁿ), interaction potentials in Modes 1 and 2 have been expressed as functions of curvatures through differential geometry.

In this paper, Mode 3, i.e., the interaction between a curved surface body and an inside particle, is studied.

A lot of mechanical phenomena can be abstracted as Mode 3. For example, in the coffee ring effect^[8], the interaction between coffee granules and water drop drives ordered motion and forms ordered pattern^[9]. In hydrogen embrittlement^[10], hydrogen atoms diffuse and accumulate in internal defect to cause cracking of metal. In a biological system, particles may move along the biomembrane nanotube^[11].

Based on the physical/mathematical model of Mode 3, this paper aims to express the interaction potential of a curved surface body and an inside particle as a function of curvatures, with which the abnormal movements of particles at small scales may be explained from the viewpoint of geometry.

2 Research approaches to Mode 3

To study Mode 3, two research approaches may be selected. One is the direct approach, and the other is the indirect approach.

The direct approach is to derive the curvature-based potential for Mode 3 directly. This approach is complex and similar to that in Modes 1 and 2. For this reason, this paper puts the direct approach in Appendix A for reference.

Based on duality, the curvature-based potential of Mode 1 may be transformed into the curvature-based potential of Mode 3, which forms the indirect approach. In fact, Modes 1 and 3 have a close relation depicted as duality. Here, duality corresponds to a kind of additive algebraic operation. Thus, we can establish simple relations between the curvature-based potential of Modes 1 and 3.

3 Dual material space and dual interaction potential

Duality is the thought that has important applications in modern science. Examples include the Poincare duality theorem in the manifold^[12] and the Desargues theorem in the projective geometry^[13].

Duality here means the complementary of material space. In Fig. 2, there is a three-dimensional infinite body V and a particle p with an equivalent radius τ inside the body. Suppose that the particle p interacts with other particles in V, and the pair-potential is u. The number density of particles in V is ρ. Then, the interaction potential between the particle p and other particles in V is

(1)

Now, we use an imaginary curved surface S to cut the infinite body V (see Fig. 3). Suppose that the nearest distance between the particle p and the surface S is h, i.e.,

(2)

As shown in Fig. 4, the infinite body V is segmented by the imaginary curved surface S into two parts, i.e., the convex body and the concave body are geometrically complementary. According to the position of particle p, two cases may be abstracted. One is that the particle p locates inside the convex body (i.e., ) and outside the concave body (i.e., ) (see Fig. 4). The other is that the particle p locates outside the convex body (i.e., ) and inside the concave body (i.e., ) (see Fig. 5). Both cases obey the complementary invariability as follows:

(3)

(4)

Correspondingly, the interaction potentials in two cases satisfy the following duality invariability:

(5)

(6)

Here,

(7)

(8)

The duality shown in Eqs.(5) and (6) brings great convenience for later study. As the interaction potentials _outer and _outer have been studied in Mode 1, the interaction potentials _inner and _inner in Mode 3 can be derived from the dual relations in Eqs.(5) and (6).

As shown in Fig. 3, if the surface S is a plane, Eqs.(5) and(6) will degenerate to

(9)

Here, U_outer and U_inner represent the interaction potential between the planar surface body (or semi-infinite body)and an outside particle or an inside particle, respectively.

Similar to the previous paper^[5-7], the pair-potential u is taken as the form of negative exponential^[15],

(10)

4 Interaction potential between semi-infinite body and inside particle

As shown in Fig. 2, based on the negative exponential pair potential in Eq.(1), the interaction potential between the infinite body V and the inside particle p is

(11)

It is noted that there is only one characteristic size in Eq.(11), i.e., the particle equivalent radius τ. For the given material, τ is a constant.

From the previous paper^[6], the interaction potential between the semi-infinite body V_outer and the outside particle p is

(12)

There is also one characteristic size in Eq.(12), i.e., the distance h.

By duality in Eq.(9), we get

(13)

In Eq.(13), there are two characteristic sizes, i.e., the particle equivalent radius τ and the distance h. Equation(13) can be further written as

(14)

where is the dimensionless interaction potential between the semi-infinite body V_inner and the inside particle p. is the ratio of two characteristic sizes,

is a dimensionless parameter of characteristic scale. Generally speaking, there is τ ≤ h or ≤ 1.

5 Interaction potential between convex curved surface body and inside particle

Firstly, Mode 3 for the convex body _inner is studied. As shown in Fig. 6, when the particle p locates inside a convex body _inner, it must be outside the dual concave body _outer at the same time (Mode 1 for _outer, see Fig. 7). Mode 3 for _inner and Mode 1 for _outer are dual.

To ensure uniformity, a unified coordinate system is used. As shown in Figs. 6 and 7, a local Cartesian coordinate system O-xyz is built at the nearest point O on the surfaceS. The x-and y-axes coincide with the tangent direction of the principle curvature lines at the point O on S. The z-axis always points to the concave side of the surface S. The distance between the point O and the particle p is h. By duality, the interaction potential for Mode 3 in Fig. 6 can be derived under such a uniform coordinate.

Under the coordinate system shown in Fig. 7, the curvature-based potential between the concave body _outer and the outside particle (Mode 1 for _outer) is^[6]

(16)

Here,

(17)

in which c₁ and c₂ are the principle curvatures, H and are the mean curvature and the dimensionless mean curvature, respectively, and K and are the Gauss curvature and the dimensionless Gauss curvature, respectively. If →0, →0, then there is _outer →U_outer, i.e., the interaction potential between a concave body and an outside particle degenerates to that between a semi-infinite body and an outside particle.

Substituting Eq.(16) into the dual relation (see Eq.(5)), we get

(18)

Equation(18) can be written as follows:

(19)

If →0, and →0, then Eq.(19) turns to

(20)

The interaction potential between a convex body and an inside particle degenerates to that between a semi-infinite body and an inside particle.

6 Curvature-based potential between concave body and inside particle

Now, we consider the case in which the particle p locates inside the concave body _inner (i.e., Mode 3 for _inner, see Fig. 8). In this case, the particlep must be outside the dual convex body _outer at the same time (i.e., Mode 1 for _outer, see Fig. 9).

The same uniform coordinate system as Figs. 6 and 7 is built (see Figs. 8 and 9). In the coordinate system in Fig. 9, the curvature-based interaction potential for Mode 1^[6] is known as

(21)

When →0, and →0, there is _outer →U_outer, i.e., the interaction potential between a convex body and an outside particle degenerates to that between a semi-infinite body and an outside particle.

Substitution of Eq.(21) into the dual relation in Eq.(6) leads to

(22)

Equation (22) can be further written as

(23)

When there is

The interaction potential between a concave body and an inside particle degenerates to that between a semi-infinite body and an inside particle.

7 Unified formulation of curvature-based potentials between convex/conc-ave body and inside particle

Equation (23) reveals that if the surface is highly curved, the effect of curvatures cannot be ignored. Thus, the movements of particles inside the curved surface body are strongly controlled by the morphology of the surface of the curved surface body.

By comparing Eq.(2) with Eq.(23), we find that the curvature-based potentials between a convex/concave body and an inside particle have small difference, that is, the sign of the term is different. Thus, in the above unified coordinate system, Eqs.(2) and (23) can be written in the unified form as follows:

(24)

8 Curvature-based driving force exerted on inside particle

Once the potential mode 3 is confirmed, the driving forces acting on the particle p can be determined. There are also two approaches to study the driving forces acting on the particle p. One is the direct approach, in which the driving forces exerted on the particle p are derived from Eq.(24) directly. The other is the indirect approach, in which the driving forces are studied by the dual relation.

This section will introduce the indirect approach and derive driving forces quantitatively by the direct approach.

8.1 Indirect approach: from dual interaction potentials to dual driving forces

The indirect approach originates from the dual relations in Eqs.(5) and (6), which can be written in a unified form of

(25)

Taking the gradient on both sides of Eq.(25) leads to

(26)

Here, ∇ is the gradient operator defined in the three-dimensional space,

(27)

where i, j, and k are base vectors in the rectangular coordinate system. The relations between the potentials and driving forces are

(28)

As is a constant, there is

(29)

Equations(26), (27), and (28) may give the dual driving forces,

(30)

Proposition may be drawn from Eq.(3). For convex and concave bodies with geometric duality, their driving forces on the particle may form an equilibrium force system.

The equilibrium relation between can be depicted in Fig. 10. Equation(30) leads to In the previous paper^[6], the driving force has been written as the function of curvatures. Thus, the curvature-based driving force acting on the particle by the dual curved surface body can be derived from Eq.(31).

(31)

From the derivation process above, a general proposition can be deduced. The curvature-based driving force acting on the particle located inside the curved surface body is independent of the equivalent radiusτ of the particle.

In Eq.(11), the equivalent radius τ of the particle p only appears in the potential . Because is a constant and ∇ is a zero vector, the equivalent radius τ only affects the interaction potentials, and does not affect the driving forces.

8.2 Direct approach: from curvature-based potential to curvature-based driving force

For convenience, all the terms in the bracket of Eq.(23) are written as a dimensional form,

(32)

8.2.1 Normal driving force acting on inside particle

Suppose that the particle p is confined to move in the normal direction z. In the coordinate system in Fig. 6, the driving force in the z-direction felt by the particle p inside the convex body is

(33)

When H=0, and K=0, Eq.(33) degenerates to the normal driving force of the particle located inside the semi-infinite body,

(34)

In Fig. 8, the normal driving force acting on the particle pinside the concave body is

(35)

Equation (35) shows that the driving force is indeed independent of the equivalent radius τ. The normal driving force F_z is strongly regulated by the curvatures of the surface of the curved surface body. This result confirms the previous proposition^[6].A curved space may induce driving forces.

8.2.2 Tangential driving force acting on inside particle

A surface with constant distance to the curved surface body, i.e., h=const., is called a parallel curved surface. Suppose that the particle is confined to move on a parallel curved surface. It will feel a tangential force in the tangent plane of the parallel curved surface (see Fig. 11),

(36)

In Eq.(36), is the gradient operator defined in the parallel curved surface,

Here, gⁱ are the natural base vectors, and uⁱ are the Gauss parameter coordinate in the parallel curved surface. Substituting Eq.(23) into Eq.(36) yields

(37)

Equation (37) shows that is also independent of the equivalent radius τ of the particle. Equation (37) indicates that not only the curvatures but also the gradients of curvatures are the fundamental elements in the tangential driving forces.

If H=0, and K=0, there is F_t=0, i.e., no tangential force is acting on the particle inside the semi-infinite body.

For a cylinder and sphere, as the gradients of curvatures are zero, the tangential driving forces acting on the inside particles are also zero.

9 Numerical verification of curvature-based potential between curved surface body and inside particle

This section verifies the accuracy of the curvature-based potential _inner. According to Eqs.(5) and (6), the accuracy of _inner is directly determined by the accuracy of curvature-based potential _outer. In the previous paper^[6], the accuracy of _outer has been verified. From the duality in Eqs.(5) and (6), it can be deduced that the accuracy of _inner is assured. Thus, this paper does not verify the effect of curvatures on _inner, but focuses on the effect of the dimensionless equivalent radius =τ/ h on the accuracy of _inner, which is listed in Tables 1 and 2.

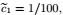
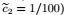
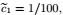
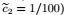
Firstly, the curvature-based potential (see Eq.(23)) is rewritten as

(38)

Equation (38) is changed to

(39)

Both sides of Eq.(39) are divided by U_inner to get the dimensionless curvature-based potential,

(40)

Secondly, both sides of Eq.(A20) in Appendix A are divided by U_inner to get the integral form of dimensionless potential,

(41)

Here, is the dimensionless coordinate of the particle. The specific definition can be found in Eq.(A16). is the dimensionless normal curvature at the point O,

(42)

Finally, are compared, and the accuracy may be estimated,

(43)

From Tables 1 and 2, we find the tendency below. The smaller the parameter is (i.e., the bigger the distance h is), the higher accuracy the curvature-based potential has. This can be easily understood from the physical diagram. The farther the particle is away from the curved surface body, the smaller the effect of the curvature is, and the higher the accuracy of the curvature-based potential is. Overall, the accuracy of curvature-based potential is very high when ranges in a broad region.

10 Potential energy gap between three basic modes

Together with the previous works^[5-7], the interaction potentials of Modes 1, 2, and 3 are all expressed as functions of curvatures marked as U_outer, U_on, and U_inner, as shown in Fig. 12.Now, we consider the potential gap between the three modes. The pair potential between the particles is written as U_n=C/R, in which a positive C means repulsive potential, while a negative Crepresents the attractive potential. U_outer, U_on, and U_inner are written as

(44a)

(44b)

(44c)

There is λ=1 for the convex body and λ=-1 for the concave body. For attractive interaction, there is U_inner < U_on < U_outer, and the particle p tends to stay inside the body under the action of the normal driving force F_z (see Fig. 13(a)). For repulsive interaction, there is U_outer < U_on < U_inner, and the particle p prefers to stay away from the body under the influence of the normal driving force F_z(see Fig. 13(b)).

When H→0, and K→0, the curved surface body changes to a semi-infinite plane body, as shown in Fig. 14. Now, the interaction potentials between the particles under three models are

(45a)

(45b)

(45c)

The interaction potential gap between three modes of particle and semi-infinite plane body is

(46)

Equation (46) indicates that when the curved surface body is fat enough, the potential gap between Modes 1 and 2 is equal to that between Modes 2 and 3.

As shown in Fig. 12, when the surface bends, the potential gap between three models is

(47a)

(47b)

(47c)

As the curvature based potential is derived based on the assumption that Hh and Kh² are small quantities, the term in Eq.(47) is a small quantity with high order and can be omitted in the following discussion. As n>4 and h≥ τ, there is

(48)

Equation (47) indicates that the potential gaps between three modes are closely related to the surface morphology, i.e., the mean curvature H. By combining Eqs.(47) and (48), we get the judgment below. For the convex body, ∆U_inner-on increases but ∆U_on-outer decreases along with the increase of the mean curvature H, while for the concave body, ∆U_inner-on decreases and ∆U_on-outer increases along with the increase of the mean curvature H.

11 Conclusions

On the basis of duality, this paper derives the curvature-based interaction potential between a curved surface body and an inside particle. From the dual geometric structures to the dual interaction potentials and driving forces, we can find that duality plays an important role. This paper confirms the proposition. The interaction potential between a curved surface body and an inside particle can be expressed as a function of surface curvatures. Besides, a highly curved surface body can induce driving forces on the inside particle, and the curvatures and the gradient of curvatures are the fundamental elements of the driving forces.

Appendix A

Similar to the approach used in the previous paper^[6], the curvature-based potential is deduced as follows.

A1 Approximation of local shape of curved surface body

Similar to the previous paper^[6], the local shape of the curved surface body V needs to be approximated to derive the curvature-based potential. As the particle p mainly interacts with the adjacent area around the point O, which is the nearest point on the curved surface body to the particle p, the local shape of curved surface body around the point O should be approximated as accurate as possible. This is a classical problem in differential geometry^[16]. Under the principal coordinate system O-xyz at the point O, the surface S of the curved surface body V can be approximated by the surface S with the analytic expression below,

(A1)

Here, c₁ and c₂ are the principal curvatures of curved surface S the point O. The curved surface body with the surfaceS is marked as V₀. The original curved surface body V is approximated by V₀, and the potential between V and the particle p is substituted by the potential between V₀ and the particle p. The local relation between V₀ and V is shown in Fig. A1.

A2 General formulation of interaction potential

As shown in Figs. A2 and A3, a spherical surface S_p is drawn with its center at the particle p and the radius R to intersect with V₀. Suppose that the area of the intersection surface between S_p and V₀ is A. Then, the interaction potential between V₀ and the particle p is

(A2)

Equation(A2) is valid for both convex V₀ and concave V₀.

A3 Unified formulation of intersection area A

In Figs. A2 and A3, when the radius R of sphere surface S_p is smaller than the nearest distance from the particle p to the curved surface S₀, the intersection area is equal to the area of sphere surface S_p, i.e.,

(A3)

In the case of R>h, in order to derive the interaction area A, a cylindrical coordinate system p-rθ z with the particle p as the pole and the x-axis as the polar axis is established. The transformation between (x, y) and (r, θ) is

(A4)

By substituting Eq.(A4) into Eq.(A1), we have

(A5)

Here,

(A6)

k_n is the normal curvature of S₀ at the point O.

For a convex body (see Fig. A2), suppose that the point B is an arbitrary point on the intersection line between S_p and S₀.Then, a vertical line is drawn from the point B to the z-axis and meets the z-axis at the point C. In the triangle ABP, there is

(A7)

Here, R_k =|CB|, and z is the coordinate of the point B in the z-axis. In the cylindrical coordinate system, there exists

(A8)

The intersection area of the sphere S_p and the convex body is

(A9)

By combining Eq.(A5) and Eq.(A7), we get the calculation formula for R_k,

(A10)

Substitution of Eq.(A10) into Eq.(A9) leads to

(A11)

For the concave body (see Fig. 12), in the triangle ABC, there is

(A12)

The intersection area is

(A13)

Combination of Eq.(A5) and Eq.(A12) may give the calculation formula for R_k,

(A14)

Substitution of Eq.(A14) into Eq.(A13) leads to

(A15)

To unify and , we define the coordinate of particle p as (0, 0, z_p), and the dimensionless coordinate is defined as

(A16)

There is for concave V₀. Obviously, by the dimensionless coordinate , Eqs.(A11) and (A15) can be unified as

(A17)

Substituting Eqs.(A17) and (A3) into Eq.(A2) to get the unified interaction potential between a convex/concave body V₀ and an inside particle p,

(A18)

A4 Curvature-based interaction potential

In Eq.(A18), k_n is the function of principal curvatures c₁, c₂, and θ. In this section, Eq.(A18) will be written as an explicit formula of two principal curvatures c₁ and c₂. It is noted that Eq.(A18) is very similar to the formulation in the previous paper^[6]. Thus, this section will still use the series expansion of small parametric variable^[17].

The shortest distance h between the particle p and S₀ is used as the characteristic length to define the dimensionless variables,

(A19)

Then, Eq.(A18) can be rewritten as

(A20)

In Eq.(A20), let

(A21)

Here, is the continuous and differentiable function of . From Eqs.(A6) and (A19), we get

(A22)

Suppose that the distance h is a small quantity compared with the curvature radius at the point O on the curved surface body,

(A23)

From Eq.(A22), _n is also a small quantity, i.e., can be taken as the small parametric variable, and the series expansion method may be used^[17]. can be expanded into Taylor's series of small parametric variable ,

(A24)

For simplification, we omit the terms with orders

(A25)

Substitution of Eq.(A25) into Eq.(A20) gives

(A26)

In Eq.(A26),

(A27)

(A28)

Substituting Eq.(A27) and Eq.(A28) into Eq.(A26) leads to the interaction potential depicted by the principal curvatures,

(A29)

Equation(A29) can be rewritten as

(A30)

Equation(A30) is exactly the same as Eq.(27).