Shanghai University
Article Information
- Mingwei GE, Guodong JIN
- Response of turbulent enstrophy to sudden implementation of spanwise wall oscillation in channel flow
- Applied Mathematics and Mechanics (English Edition), 2017, 38(8): 1159-1170.
- http://dx.doi.org/10.1007/s10483-017-2226-9
Article History
- Received Oct. 3, 2016
- Revised Dec. 21, 2016
2. State Key Laboratory of Nonlinear Mechanics, Institute of Mechanics, Chinese Academy of Sciences, Beijing 100080, China
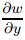 , the turn of ωz by
, the turn of ωz by 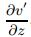 , and the horizontal shear of ωz by
, and the horizontal shear of ωz by 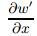 are suppressed due to the presence of SWO, leading to attenuation of the turbulent enstrophy.
are suppressed due to the presence of SWO, leading to attenuation of the turbulent enstrophy.
Drag reduction is an important issue in fluid mechanics, which has attracted more and more interest recently owing to its potential of decreasing energy consumption in industry. Generally, drag reduction control can be divided into active control and passive control. Passive control, which keeps the control measures constant during the work, does not require energy input from the external environment and is very convenient for application such as the riblets[1-3] and hydrophobic surface[4-7]. However, most of them are criticized for their low drag reduction rate and bad environmental adaptability. Active control is developed to avoid the disadvantages of passive control. It can obtain very substantial drag reduction but needs additional energy input. Furthermore, active control can be grouped into feedback control which needs sophisticated feedback control systems, and open-loop control which needs additional energy input without feedback. In this paper, open-loop active control is mainly concerned.
For the open-loop active control schemes, the spanwise wall oscillation has been extensively studied due to its significant drag reduction rate[8-11]. The suppression of turbulence by spanwise wall oscillation (SWO) in a canonical channel flow was first investigated by Jung et al.[12] via direct numerical simulation, and a 40% frictional drag reduction was obtained. Soon afterwards, the numerical results were verified by Laadhari et al.[13] and Choi et al.[14] in a turbulent boundary layer through physical experiments. Through direct numerical simulation of a pipe flow with circumferential wall oscillations, Quadrio and Sibilla[15] attributed the drag reduction to the tangential advection arising from the Stokes layer. After a similar simulation, Choi and Graham[16] claimed that the oscillations affect the relations between the near-wall streamwise vortices and low-and high-speed fluids, and then suppress the production of Reynolds shear stress. Focusing on the initial behavior of the Reynolds stress to the harmonic oscillations, Xu and Huang[17] found that the motions of the wall attenuate the distribution term in the transport equations and finally suppress the turbulence. Different from the analyses of the long-term drag reduced condition, the study of the response of the wall bounded turbulent flow to a sudden spanwise wall oscillation can provide more details of the flow evolution[18]. Recently, Ricco et al.[19] studied the global turbulent enstrophy to the wall oscillation in a very short time in a turbulent channel flow. They found that in the beginning stage, after a sudden implementation of spanwise oscillations, the turbulent enstrophy shows a transient increase which directly enhances the turbulent dissipation. As a consequence, the activity of turbulence is suppressed by the transient increase of the turbulent enstrophy in the initial phase, which drifts the turbulent flow towards a new lower-drag condition after a long time. The understanding of the mechanism of drag reduction by the harmonic wall oscillations has been greatly pushed forward by the efforts of many scientists. However, the whole picture of the mechanism for drag reduction is still not clear, and there are some problems not enclosed. In the work of Ricco et al.[19], the transient growth of the turbulent enstrophy was emphasized. However, the reason for the transient growth as well as the evolution of the turbulent enstrophy after the transient growth is still not clear.
In this paper, the transport of the turbulent enstrophy is studied in detail in a turbulent channel flow subjected to sudden wall oscillations. The objective of this work is to gain a furth-er insight into the mechanism for drag reduction by wall oscillations on the aspect of vortical dynamics. The transient growth and the transport of the turbulent enstrophy on the initial stage are analyzed.
2 Numerical calculations and flow configuration 2.1 Numerical methodsThe turbulent flow between two infinite parallel flat plates with oscillating walls is studied through direct numerical simulation. The Navier-Stokes equations for the incompressible Newtonian fluid are taken as the governing equations,

|
(1) |

|
(2) |
where ui is the ith component of the flow velocity, t is the time, ρ is the density of fluid, and p is the pressure. All the flow variables are dimensionless through the wall frictional velocity uτ and the kinematic viscosity of the fluid ν, of which 

|
(3) |

|
| Fig. 1 Computational domain and coordinate system |
|
|
Here, we select the amplitude of the oscillation W=12 and the cycle T=100 following the optimal case by Ricco et al.[19]. A pseudo-spectral method is used to solve the three-dimensional Navier-Stokes equations. The Fourier Galerkin and Chebyshev-Tau methods are used for spatial discretization of the channel flow, and a third-order time splitting method is adopted for advance of time. The direct numerical simulation method has been well validated by Xu el al.[20] and Ge et al.[21]. The computational domain spans 4π×2×2π in the streamwise, wall normal, and spanwise directions, respectively, in accordance with the 128×129×128 grids. During numerical simulation, the pressure gradient is kept constant, and hence the flow rate increases with the evolution of turbulence due to the drag reduction.
2.2 Flow field decompositionBefore we proceed further, some types of average operators are introduced here. We assume that there is a flow quantity f(x, y, z, t), and it can be decomposed as[22]

|
(4) |
where the variable with the tilde head denotes the periodic fluctuation due to the SWO, and the one with the superscript denotes the stochastic fluctuation. In this paper, the turbulent enstrophy is referred to as ωi' ωi'. The mean value of a quantity is defined as

|
(5) |
where

|
(6) |
Hence,

|
(7) |

|
(8) |
A global quantity for an instantaneous flow field is defined as

|
(9) |
The comprehensive global quantity can be defined as

|
(10) |
Figures 2(a) and 2(b) show time traces of the space-averaged streamwise skin friction and the flow rate after the application of SWO at t=0, respectively. In the early stage of the implementation of SWO, the skin friction reduces sharply, and hence the balance between the friction drag and the driven pressure is broken down, which then results in a quick growth of the flow rate of the turbulent channel. After a long time evolution, the turbulent channel flow achieves a new statistical steady state with lower drag coefficient. Noteworthily, under the constant pressure gradient, drag reduction does not show a real decrease of skin friction in the new statistical state. It manifests itself in terms of the increase of the flow rate. Following Kasagi et al.[23], the skin friction coefficient is defined as Cf=2/Ub2, where Ub represents the bulk mean velocity, and the drag reduction rate is defined as the change of Cf,

|
| Fig. 2 some basic statistics with swo applied at t=0 |
|
|

|
(11) |
where rf0 denotes the time and space averaged flow rate of the initial state, while rf is the flow rate of the new state after the SWO. For the case in the present paper, a drag reduction about 31% is obtained, which shows good agreement with Ricco et al.[19], in which Reτ was selected to be 200. Similar drag reductions were also obtained by Choi et al.[16] and Ricco and Wu[24] through physical experiments. Figure 2(c) shows the distribution of velocity fluctuations along y+. As can be observed, the fluctuating velocities are only affected in the near wall region y+ < 40. The maximum value of < u'u'> reduces about 30%, and the peak value location is shifted from y+≈ 19 to y+≈ 14. Due to the SWO, < w'w'>is obviously enhanced near the wall. The maximum value of < w'w'> increases about 30%, and its location is shifted closer to the wall. Different from the previous two components of velocity fluctuations, < v'v'>seems almost unchanged in the presence of SWO. Figure 2(d) shows the vorticity fluctuations along y+. Obviously, the vorticity fluctuations are also influenced by the SWO only in the near wall region y+ < 60. In the near wall region, ωx is substantially excited, while ωy is obviously refrained. Compared with the previous two components, the change of ωz' is more complex. In the sublayer, ωz' is greatly suppressed, while in the region 5 < y+ < 60, it is repressed to a lower degree.
When periodic oscillations are applied to the walls of the parallel flat channel, the physical problem can be simplified to the Stokes' second problem, and the spanwise velocity of the flow field can be analytically solved as[25]

|
(12) |
Figure 3 shows the phase-averaged spanwise velocity from both the present direct numerical simulation and the analytical solution obtained from Eq.(12). The numerical results agree well with the analytical results of the Stokes' problem. The results of the basic statistics shown here give a firm validation of the present numerical methods and also briefly show the response of the flow field to the SWO.

|
| Fig. 3 Phase-averaged spanwise velocity for different phases |
|
|
Turbulent enstrophy is the criterion of the intensity of vorticity fluctuations, which plays an important role in the evolution of the turbulent flow. Moreover, in the case of turbulent channel flow with the SWO, the global turbulent enstrophy can be mathematically regarded as the equality of the global turbulent dissipation[19]. Hence, investigation of the transport of the turbulent enstrophy is of great importance to understand the mechanism of drag reduction due to the SWO. The turbulent enstrophy can be divided into three parts: ωx' ωx'(etx), ωy' ωy'(ety), and ωz' ωz'(etz). Figure 4 shows the temporal evolution of the instantaneous global quantity of etx, ety, etz and the turbulent enstrophy. It is evident that in the beginning t < 50, there is a transient growth for turbulent enstrophy due to the SWO. This means that the dissipation which is mathematically equal to the global turbulent enstrophy increases transiently at the beginning after the application of SWO. As announced by Ricco et al.[19], the activity of turbulence is dissipated by the initial increase of dissipated term and then set into a state with lower turbulent kinetic energy. The decrease of turbulent kinetic energy for the instantaneous channel flow means a laminarization which causes a rapid decrease of the Reynolds stress and results in a lower skin friction. Note that the flow rate keeps almost unchanged in such a short time. Hence, the flow is accelerated due to the constant pressure gradient, as shown in Fig. 2(b). As the mass flow rate increases, the skin friction increases gradually. Finally, the pressure gradient and the skin friction achieve a new balance. At the new state, the friction drag normalized by its initial value varies around 1 (see Fig. 2(a)). Recall that, in the present case, the drag reduction does not show a real decrease of skin friction in the new quasi-steady state under the constant pressure gradient. Through a careful investigation on the energy balance of the channel flow with SWO, Ricco et al.[19] found that a higher proportion of energy input by pressure gradient was dissipated by the viscous effect, and a lower proportion of the energy was dissipated by the turbulent effect compared with the canonical channel flow. The results indicate that the flow tends to be laminar with the decrease of Cf in the whole process. Obviously, the transient growth of turbulent enstrophy (dissipation) plays a very important role in the evolution of the turbulent flow after the application of the SWO. As shown in Fig. 4, the transient increase of turbulent enstrophy can be then attributed to the initial growth of etz. Hence, in the next step, the response of the related terms in the transport equations of etz will be analyzed first. After that, the transport of the other two parts will be studied.

|
| Fig. 4 Time traces of instantaneous global quantities of etx, ety, etz, and et (et denotes turbulent enstrophy, and SWO starts at t=0) |
|
|
The transport equation for the global etz can be written as

|
(13) |
where P31 to P37 denote the contribution to the global etz from the production terms of ωz'. P31, P32, P33, and P37 are the production terms related to the average flow. P31 is the contribution induced by the tilting of ωy' by the spanwise mean shear. P32 is induced by the turn of ωx by 

Time traces of the production terms of etz in Eq.(13) are shown in Fig. 5. The transport of etz is mainly dominated by P31, P32, P33, and P34. At the beginning, P31 exhibits an acute increase after the SWO, while all the other terms change more insensitively. Attributed to the dominated role of P31 in the transport of etz, both the peak values of et and etz appear at about t=20, which is very close to that of P31. Evidently, it is the prime increase of P31 that results in the initial increase of etz and then et. In other words, it is the tilting of ωy' by the spanwise mean shear that induces the transient increase of et, and then represses the turbulent kinetic energy. To find the reason of the transient increase of P31, the term can be decomposed into two parts, ωz' and 


|
| Fig. 5 Time traces of production terms of etz (SWO starts at t=0), where all terms are multiplied by scale factor of 100 |
|
|

|
Fig. 6 Relationship between ωz' and ω y' |
|
|
Figure 7 shows the evolution of the correlation between ωz' and ωy'. In the flat channel before the SWO, ωz' and ωy' are two separate quantities. However, due to the effect of SWO, a substantial negative correlation forms at t=T/8. With the increase of the spanwise wall shear, the correlation increases to a higher degree at t=T/4. The results show that under the negative spanwise shear stress, the positive ωz' tends to appear at the location where ωy' is negative, and the negative ωz' tends to appear at the location where ωy' is positive. Figure 7(d) shows the schematic of the mechanism of the correlation. Assume a position in the flow filed with a positive ωy' due to the SWO. A new negative ωz' will be produced by the effect of ωy' and the negative 

|
| Fig. 7 Evolution of correlation between ωz' and ωy' |
|
|
After the transient increase, etz decreases dramatically, and the attenuation is beyond 50% at t=400. As is shown in Fig. 5, the attenuation of etz can be mainly attributed to the inhibition of the terms P31, P33, P35, and P36. It should be pointed out that although the term P31 is a new term compared with the initial state, the rapid minimizing of this term still makes important sense. Assume that, if the term P31 keeps the peak value at t=20 in the entire process of evolution, the attenuation of etz will be much slower. From the physical sense, the terms P31 and P35 can be regarded as a whole induced from the turn of ω y' by 
In this section, the transport of ety and etx is mainly focused. The transport equation for the global ety can be written as

|
(14) |
where P21 and P22 are induced by the inclination of ωx and ωz, while P23 and P25 are generated by the inclination of ωx' and ωz', respectively, and the term P24 is generated by the stretching of ωy'. Figure 8 shows the evolution of the production terms of ety in the initial stage after the SWO. Evidently, the suppression of ety is mainly dominated by the terms P22 and P24 which result from the inclination of ωz and the stretching of ωy', respectively. Different from the transport of etz, the term P21, which is directly related to the spanwise mean shear, only plays a secondary role here.

|
| Fig. 8 Time traces of production terms of ety (SWO starts at t=0), where all terms are multiplied by scale factor of 100 |
|
|
The transport equation for the global etx can be written as

|
(15) |
where P11 is generated from the inclination of ωy' by the streamwise mean shear, P12 is the production term of etx from the contribution of the stretching of ωx, P13 is induced by the tilting of ωz by 

|
(16) |
The terms P15 and P16 can be expanded as

|
(17) |

|
(18) |
The order-of-magnitude analysis taken by Ricco et al.[19] is adopted here. The length scale of the disturbance along x can be taken as λx=O(1000), namely, the characteristic length of the low-speed streaks, while the length scale of the distance along the z-axis can be taken as λz=O(100), denoting that the characteristic spacing of the low-speed streaks. For the turbulent channel with the SWO, when T=100, the length scale along the y-axis can be assumed as λy=O(10). Through the order-of-magnitude analysis, it is easy to get the results that the term 15a is much larger than the term 15b in Eq.(17), and the term 16a is much smaller than 16b in Eq.(18). Through a careful inspection of Eqs.(17) and (18), it is found that the main contributors of the two equations are opposite to each other. Hence, the terms P15 and P16 can be put together as a whole with only the secondary terms left.
The evolution of the production terms of etx is shown in Fig. 9. Compared with the evolutions of the ety and etz, the evolution of etx seems a little slower, as shown in Fig. 4. The term P12 which directly relates with the SWO only plays a minor role in the evolution of etx. Instead, the term Pc13 combined with the term P14 play as the dominate contributors. In the beginning t < 50, a transient growth occurs on etx, after that etx is suppressed. A similar evolution process can also be observed for the terms Pc13 and P14. Hence, both the transient growth of etx in the initial stage and the attenuation of etx after the beginning can be attributed to the term Pc13 due to the horizontal shear of ωz and the term P14 due to the stretching of ωx'.

|
| Fig. 9 Time traces of production terms of etx(SWO starts at t=0), where all terms are multiplied by scale factor of 100 |
|
|
The transport of turbulent enstrophy after the SWO is studied in detail in a turbulent channel flow. The initial transient increase of the turbulent enstrophy as well as the suppression of the turbulent enstrophy after the beginning are focused, aiming to reveal the effect of the SWO in the aspect of vortical dynamics. For clarity, the turbulent enstrophy is divided into three parts: ωx'ωx'(etx), ωy' ωy'(ety), and ωz' ωz'(etz).
The transport of etz is dominated by P31 (contribution induced by the tilting of ωy' by the spanwise mean shear), P33 (contribution from the stretching of ωz by the fluctuating quantity 
The attenuation of ety in the initial stage can be ascribed to the terms related to the inclination of ωz and the stretching of ωy'. Compared with the response of ety and etz to the SWO, the response of etx is much slower. The transient growth of etx in the initial stage as well as the attenuation of etx after the beginning of SWO can both be attributed to the change of the stretching of ωx' and the horizontal shear of ωz due to the SWO.
| [1] | Bechert, D. W., Bruse, M., Hage, W., van der Hoeven, J. G. T., and Hoppe, G. Experiments on drag-reducing surfaces and their optimization with an adjustable geometry. Journal of Fluid Mechanics, 338, 59-87 (1997) doi:10.1017/S0022112096004673 |
| [2] | Garcia-Mayoral, R. and Jiménez, J. Hydrodynamic stability and breakdown of the viscous regime over riblets. Journal of Fluid Mechanics, 678, 317-347 (2011) doi:10.1017/jfm.2011.114 |
| [3] | Viswanath, P. R. Aircraft viscous drag reduction using riblets. Progress in Aerospace Sciences, 38(6), 571-600 (2002) |
| [4] | Aljallis, E., Sarshar, M. A., Datla, R., Sikka, V., Jones, A., and Choi, C. H. Experimental study of skin friction drag reduction on super hydrophobic flat plates in high Reynolds number boundary layer flow. Physics of Fluids, 25(2), 025103 (2013) doi:10.1063/1.4791602 |
| [5] | Rothstein, J. P. Slip on superhydrophobic surfaces. Annual Review of Fluid Mechanics, 42(1), 89-109 (2010) doi:10.1146/annurev-fluid-121108-145558 |
| [6] | Rastegari, A. and Akhavan, R. On the mechanism of turbulent drag reduction with superhydrophobic surfaces. Journal of Fluid Mechanics, 773, R4 (2015) doi:10.1017/jfm.2015.266 |
| [7] | Luo, Y., Wang, L., Lork, G., Song, K., Wang, L., and Robert, S. Advances of drag-reducing surface technologies in turbulence based on boundary layer control. Journal of Hydrodynamics, 27(4), 473-487 (2015) doi:10.1016/S1001-6058(15)60507-8 |
| [8] | Quadrio, M. and Ricco, P. Critical assessment of turbulent drag reduction through spanwise wall oscillations. Journal of Fluid Mechanics, 521(12), 251-271 (2004) |
| [9] | Yakeno, A., Hasegawa, Y., and Kasagi, N. Modification of quasi-streamwise vortical structure in a drag-reduced turbulent channel flow with spanwise wall oscillation. Physics of Fluids, 26(8), 085109 (2014) doi:10.1063/1.4893903 |
| [10] | Agostini, L., Touber, E., and Leschziner, M. A. Spanwise oscillatory wall motion in channel flow:drag-reduction mechanisms inferred from DNS-predicted phase-wise property variations at Reτ=1000. Journal of Fluid Mechanics, 743, 606-635 (2014) doi:10.1017/jfm.2014.40 |
| [11] | Blesbois, O. and Chernyshenko, S. I. Pattern prediction by linear analysis of turbulent flow with drag reduction by wall oscillation. Journal of Fluid Mechanics, 724(2), 607-641 (2013) |
| [12] | Jung, W. J., Mangiavacchi, N., and Akhavan, R. Suppression of turbulence in wall-bounded flows by high-frequency spanwise oscillations. Physics of Fluids, 4(8), 1605-1607 (1992) doi:10.1063/1.858381 |
| [13] | Laadhari, F., Skandaji, L., and Morel, R. Turbulence reduction in a boundary layer by a local spanwise oscillating surface. Physics of Fluids, 10(6), 3218-3220 (1994) |
| [14] | Choi, K. S., Debisschop, J. R., and Clayton, B. R. Turbulent boundary-Layer control by means of spanwise-wall oscillation. AIAA Journal, 36(7), 1157-1163 (1998) doi:10.2514/2.526 |
| [15] | Quadrio, M. and Sibilla, S. Numerical simulation of turbulent flow in a pipe oscillating around its axis. Journal of Fluid Mechanics, 424(14), 217-241 (2000) |
| [16] | Choi, K. S. and Graham, M. Drag reduction of turbulent pipe flows by circular-wall oscillation. Physics of Fluids, 10(1), 7-9 (1998) doi:10.1063/1.869538 |
| [17] | Xu, C. X. and Huang, W. X. Transient response of Reynolds stress transport to spanwise wall oscillation in a turbulent channel flow. Physics of Fluids, 17(1), 018101 (2005) doi:10.1063/1.1827274 |
| [18] | Quadrio, M. and Ricco, P. Initial response of a turbulent channel flow to spanwise oscillation of the walls. Journal of Turbulence, 4(7), 1-23 (2003) |
| [19] | Ricco, P., Ottonelli, C., Hasegawa, Y., and Quadrio, M. Changes in turbulent dissipation in a channel flow with oscillating walls. Journal of Fluid Mechanics, 700, 77-104 (2012) doi:10.1017/jfm.2012.97 |
| [20] | Xu, C., Zhang, Z., Toonder, J. M. J. D., and Nieuwstadt, F. T. M. Origin of high kurtosis levels in the viscous sublayer, direct numerical simulation and experiment. Physics of Fluids, 8(7), 1938-1944 (1996) doi:10.1063/1.868973 |
| [21] | Ge, M., Xu, C., and Cui, G. Direct numerical simulation of flow in channel with time-dependent wall geometry. Applied Mathematics and Mechanics (English Edition), 31(1), 97-108 (2010) doi:10.1007/s10483-010-0110-x |
| [22] | Touber, E. and Leschziner, M. A. Near-wall streak modification by spanwise oscillatory wall motion and drag-reduction mechanisms. Journal of Fluid Mechanics, 693(2), 150-200 (2012) |
| [23] | Kasagi, N., Hasegawa, Y., and Fukagata, K. Toward cost-effective control of wall turbulence for skin friction drag reduction. Advances in Turbulence, 52(1), 189-200 (2009) |
| [24] | Ricco, P. and Wu, S. On the effects of lateral wall oscillations on a turbulent boundary layer. Experimental Thermal and Fluid Science, 29(1), 41-52 (2004) doi:10.1016/j.expthermflusci.2004.01.010 |
| [25] | Choi, J. I., Xu, C. X., and Sung, H. J. Drag reduction by spanwise wall oscillation in wall-bounded turbulent flows. AIAA Journal, 40(5), 842-850 (2002) doi:10.2514/2.1750 |
 2017, Vol. 38
2017, Vol. 38


