1 Introduction

The mathematical pendulum model is a classic model in dynamics and control, which is also be named as the simple pendulum model for the simple mathematical form controlling the motion of the mathematical pendulum. However, even for the simpler classic models, such as the oscillator system, different numerical schemes will obtain the numerical results with different structure-preserving properties^[1], which is the main motivation of this paper.

Since the last century, various numerical methods for the mathematical pendulum model have been reported, and various dynamic properties of mathematical pendulum model have been revealed. Balakirev et al.^[2] investigated the nonlinear dynamics of mathematical pendulum with a vibrating hanger. Moauro and Negrini^[3] proved the non-integrability and existence of chaotic trajectories in the high-energy zone for a double mathematical pendulum with certain constraints on the ratio of the masses. Martynyuk and Nikitina^[4-5] studied the motion of the mathematical pendulum, and found that conditionally periodical and chaotic trajectories of a double mathematical pendulum exist when the ratio of the pendulum masses is not small, and illustrated that conditionally periodical and chaotic paths of a system of connected mathematical pendulums exist for considerable ratios of the masses. Shaikhet^[6] and Hatvani^[7] investigated the stability of the mathematical pendulum model. Dittrich^[8] introduced double-periodic elliptic functions on the basis of the mathematical pendulum. Recently, Jerman and Hribar^[9] studied the horizontal inertial forces imparted by the load in the case of the linear motion of the pivot on the mathematical pendulum by means of an appropriate mathematical model.

The above numerical investigations on the dynamic properties of mathematical pendulum model were mainly focused on the numerical precision and ignored the inherent geometric properties of the mathematical pendulum model. To investigate the inherent geometric properties of the dynamic system, a symplectic method which is a typical structure-preserving method, was proposed by Feng^[10] in the proceeding of the 1984 Beijing symposium on differential geometry and differential equations. The main idea of the symplectic method is to preserve the symplectic structure of the dynamic system in each time step with a certain symplectic scheme^[11]. Since then, various structure-preserving discrete methods have been developed, and the structure-preserving property has been considered an important factor of a certain numerical method^[12-14].

The Störmer-Verlet scheme, a classic numerical method that was proposed by Störmer^[15] and Verlet^[16] together for the molecular dynamics simulation, has been proven to be a symplectic scheme for some ordinary differential equation systems^{[1, 12, 17-18]}, including the governing equation of the mathematical pendulum model. Inspired by the Störmer-Verlet integration algorithm, Terze et al.^[19] presented a novel second-order conservative Lie-group geometric method for integration of rigid body rotational dynamics, which was proven to be a fully explicit scheme that exactly conserves spatial angular momentum of a free spinning body. Recently, Hairer and Lubich^[20] investigated the long-time behaviour of the Störmer-Verlet-leapfrog method when this method was applied to highly oscillatory Hamiltonian systems with a slowly varying and solution-dependent high frequency. Although the excellent structure-preserving characteristics of the Störmer-Verlet method have been verified, the query of structure-preserving properties for the symplectic method in the frequency domain proposed recently^[21] motivates us to further investigate the structure-preserving properties of the Störmer-Verlet scheme in the frequency domain.

In this paper, focusing on the structure-preserving properties both in the time domain and in the frequency domain, the Störmer-Verlet scheme for the mathematical pendulum model is investigated in detail. And the phase correction method is used to improve the structure-preserving properties of the Störmer-Verlet scheme in the frequency domain, which can also be generalized to other symplectic methods. The method and the results presented in this paper can help us understand the structure-preserving properties of the Störmer-Verlet scheme comprehensively.

2 Störmer-Verlet scheme for mathematical pendulum model

In this paper, a mathematical pendulum of the length l with a particle of the mass m located at its end, as shown in Fig. 1, is considered.

Different from the classic simple pendulum, the amplitude need not be assumed to be small enough to insure the approximation sin q ≈ q in our model. In Fig. 1, the angular speed of the pendulum ball is . Based on the geometrical relationship, its speed along the arc of the circle is . The relationship between the motion and the external force can be described by the Newton's second law, i.e., , where the external force along the arc of the circle is given by F = −mgsinq. Here, g is the gravitational acceleration. Then, the governing equation of the mathematical pendulum model can be obtained,

(1)

which has been established three hundred years ago.

To simplify the analyzing process, the model (1) is usually linearized by sin q ≈ q with the small-angle assumption (usually, let q < 5°). Then, the model (1) is degenerated to the linear form that was investigated in Ref. [18] with l=1 and g=1. Unfortunately, the linearization covers up many interesting nonlinear phenomena in the mathematical pendulum model. Moreover, the small-angle assumption limits the applications of the model in engineering. Thus, in this paper, the linearization will not be performed.

It is well known that the mathematical pendulum model is a conservative system, which implies that the total energy, as well as the kinetic and potential energies, is a basic conserved quantity. In the following text, this conservation law will be formulated firstly in the Hamiltonian framework.

To simplify the mathematical formulations in the following text, the length is assumed l=1, the mass of the pendulum is assumed m=1, and the gravitational acceleration is assumed g=1.

The kinetic energy of the pendulum system is

(2)

and the potential energy of the pendulum system is

(3)

Then, the total energy of the pendulum system is

(4)

It has been mentioned that the total energy of the pendulum system is a conserved quantity, that is,

(5)

With the Newton's second law , which means (let the integration constant be zero), the conservation law of the total energy can be rewritten as

(6)

in which () is just the Hamiltonian function of the pendulum system, that is,

(7)

With the Hamiltonian function, the mathematical pendulum model (1) can be written in the Hamiltonian canonical form,

(8)

from which it can be easily found that there is periodicity T=2π, i.e.,

(9)

To investigate the structure-preserving properties of the numerical scheme for the Hamiltonian canonical form (8), it is necessary to define the state variable as u = (p, q)^T ∈ R². Then, Eq. (8) can be rewritten as a more compact form^[9],

(10)

with

(11)

where is the skew-symplectic matrix.

For the second-order differential equation (1) with , the most natural discretization is

(12)

where h is the step length. (12) is just obtained by replacing the second derivative in Eq. (1) with the central second-order differential quotient.

It has been proven that the scheme (12) is not structure-preserving at all. Thus, Störmer^[15] used high-order variants for numerical computations concerning the aurora borealis. Then, Verlet^[16] applied this method for the computation works in molecular dynamics. Finally, this method was named as the Störmer-Verlet method. The Störmer-Verlet scheme of Hamiltonian canonical form (8) is

(13)

and the recurrence operator can be written as

(14)

From (14), the following recurrence relationship for the Störmer-Verlet scheme is obtained according to the outline of Refs. [12] and [18]:

(15)

which implies that is a conservative quantity in the Störmer-Verlet scheme (13).

3 Numerical experiments on Störmer-Verlet scheme

To test the structure-preserving properties of the Störmer-Verlet scheme (13) for the mathematical pendulum system, numerical experiments are performed with the same initial value (p, q)^T|_t=0 = (1, 0)^T in this section, which means that the initial value of the Hamiltonian function is .

By assuming the time step length as h=0.50, 0.10, 0.05, 0.01, respectively, the motion process of the mathematical pendulum is simulated by the Störmer-Verlet scheme (13), and the absolute errors of the Hamiltonian function ∆H_n = |H₀ − H_n| in each step are shown in Fig. 2.

From Fig. 2, it can be found that, the errors of the Hamiltonian function are less then 4× 10^-8 with different time step lengths. Moreover, the amplitudes of the Hamiltonian function errors are almost independent of the time step length, which implies that the total energy can be preserved by the Störmer-Verlet scheme (13) well.

As important geometric characteristics of the pendulum model (1), the conservation law of periodicity (9) should also be taken into account. Thus, the relationships between and q are recorded in each time step in the simulation process. Moreover, the periodicity of and the periodicity relative errors defined as with different time step lengths are listed in Table 1.

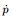
From Table 1, it can be found that the periodicity conservation law (9) cannot be preserved exactly even if h=0.01. With the decrease in the time step length, the periodicity relative errors decrease, and the periodicity of in the numerical results is much closer to 2π, which implies that the preserving performance of the periodicity conservation law (9) with the Störmer-Verlet scheme (13) is dependent on the value of the time step length. However, it is well known that, as a finite difference scheme, the decrease in the time step length will lower the computational efficiency of the Störmer-Verlet scheme (13). Thus, to improve this weakness of the Störmer-Verlet scheme (13), the phase drift of the numerical solution will be corrected partly in the following section.

4 Phase correction on Störmer-Verlet scheme

In Section 3, it has been shown that the Störmer-Verlet scheme (13) can preserve the total energy well. However, the preserving performance of the periodicity conservation law (9) is dependent on the time step length. The error of the periodicity conservation law results from the phase drift in the Störmer-Verlet scheme (13). The existence of the phase error of the symplectic method was first found by Görtz^[22] based on the backward error analysis of symplectic integrators, and the phase correction method was proposed by Xing and Yang^[21] to deal with the phase error problem of the symplectic method recently.

In this section, the phase error of the Störmer-Verlet scheme (13) will be corrected partly according to the method given by Xing and Yang^[21].

By following the outline of the correction method in Ref. ^[21], the single-step phase error of the Störmer-Verlet scheme (13) can be estimated approximately as

(16)

where ω =1 can be obtained from the relationship , and . Thus, with the time step length h, the single-step phase error of the Störmer-Verlet scheme (13) is

(17)

Thus, to eliminate the single-step phase error of the Störmer-Verlet scheme (13), the following single-step time coordinate correction should be performed:

(18)

With this time coordinate correction, the motion of the mathematical pendulum model is simulated again with h=0.50, 0.10, 0.05, 0.01, respectively. The absolute errors of the Hamiltonian function are shown in Fig. 3, and the periodicity relative errors with different time step lengths are listed in Table 2.

Comparing the absolute errors of the Hamiltonian function before the phase correction (see Fig. 2) with those after the phase correction (see Fig. 3), the upper bounds of the Hamiltonian function error are almost invariable after the phase correction is performed, which implies that the conservation law on the total energy of the Störmer-Verlet scheme (13) is independent of the phase drift of the scheme (13).

From the periodicity relative errors with different time step lengths after the phase correction shown in Table 2, it can be found that the phase drift phenomenon is improved obviously when the phase correction is performed. After the phase correction, the period of is close to 2π ≈ 6.283 126 even if h=0.50. However, note that the phase drift phenomena still exist, and the phase drift level is still dependent on the value of the time step length after the phase correction is performed for the Störmer-Verlet scheme (13), which implies that the phase correction proposed in this paper cannot eliminate the phase drift phenomena completely but can weaken the phase drift phenomena in the structure-preserving method

5 Conclusions

Traditional structure-preserving methods, including the symplectic method and the multi-symplectic method, have been paid more attention to the conservation law in the time domain when the conservation law in the frequency domain is ignored. Taking the mathematical pendulum model as an example, the Störmer-Verlet scheme, proven to be a structure-preserving scheme for some finite dimension dynamics systems, is constructed for the mathematical pendulum model, and the conservation law of total energy as well as periodicity is deduced. The numerical experiments on the pendulum model are performed to investigate the structure-preserving properties of the Störmer-Verlet scheme. Aiming at the phase drift resulting from the Störmer-Verlet scheme, the phase correction is used, and the correcting effect is illustrated with the numerical results. From the numerical results, it can be concluded that

(1) The Störmer-Verlet scheme can preserve the total energy well but cannot preserve the periodicity of the pendulum even if the time step is small;

(2) The phase correction performed for the Störmer-Verlet scheme can weaken the phase drift phenomena without affecting the structure-preserving characteristics of the total energy.