1 Introduction

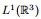In this paper, we investigate the following Navier-Stokes-Landau-Lifshitz system:

(1a)

(1b)

(1c)

where , u(x, t) is the velocity field, d(x, t) is the magnetic moment, and the symbol ∇d⊙∇d denotes a 3×3 matrix whose (i, j)th entry is given by ∂_id·∂_jd for 1≤i, j≤3. (1a) and (1b) are the well-known Navier-Stokes equations, while (1c) is the Landau-Lifshitz system when u≡0. When the term d×Δd is omitted, the system (1) reduces to liquid crystals which have been studied by many researchers. Lin et al.^[1] established the global existence of a unique "almost strong" solution that has at most finitely much possible singular time which is analogous to that for the heat flows of harmonic maps (see Ref. [2]) for the initial boundary value problem in bounded domains in two dimensions (see Ref. [3] for some related works). However, the global existence of weak solutions in three dimensions remains an open problem. For strong solutions, Li and Wang^[4], Lin and Ding^[5], Wang^[6], Hineman and Wang^[7] studied the global existence of strong solutions with small initial data and the local existence of strong solutions with any initial data. Recently, the decay of smooth solutions to the non-isothermal model for compressible nematic liquid crystals has been studied by Guo et al.^[8]. An approximate model of liquid crystals system by the Ginzburg-Landau function was studied^[9-11], i.e., |∇d|²d was replaced by with ε > 0, and the large time behavior of solutions in the whole space was shown.

Many works have been done on the global stability of the near-constant-equilibrium solutions to the Cauchy problem or the initial boundary value problem of the compressible Navier-Stokes equations. Matsumura and Nishida^[12] proved the global existence of small solutions in the H³-norm and established the first-order spatial derivatives of solutions in the H¹-norm in . At the same time, under an assumption that the small initial disturbance belongs to , Matsumura and Nishida^[13] obtained the following convergence rate:

for any t≥0. For the small initial perturbation belonging to H³ only, Matsumura^[14] used the weighted energy method to show the time decay rates

for k=1, 2, and

For the spatial dimension n=2 or 3 of the same system, if the small initial disturbance belongs to , Ponce^[15] obtained the optimal L^p convergence rate

for 2≤p≤∞ and k=0, 1, and 2. In order to establish optimal decay rates for higher-order spatial derivatives of solutions, if the initial perturbation is bounded in the H^-s-norm instead of L¹-norm, Guo and Wang^[16] developed the time convergence rates as follows by using a general energy method:

for 0≤k≤N-1. For more results, readers can also refer to Refs. [17]-[21] and references therein. For the classical incompressible Navier-Stokes equations, the readers can refer to Refs. [22]-[26]. Schonbek^[25] and Schonbek and Wiegner^[26] used the Fourier splitting method^[24] and inductive argument to establish optimal decay rates for higher-order derivatives norm after having the optimal decay rates of solutions and its first-order spatial derivatives at hand. Recently, by using the Fourier analysis and standard techniques, Liu and Gao^[27] proved global well-posedness and long time decay of the three-dimensional Boussinesq equations.

As for the system (1), Zhai et al.^[28] obtained the global existence of a unique solution without any small conditions imposed on the third component of the initial velocity field relying upon the Fourier frequency localization and Bony's paraproduct decomposition. When the density is also considered, by using energy methods and delicate estimates from the harmonic analysis, Fan et al.^[29] obtained regularity criteria for the strong solutions of the system (1) in Besov and multiplier spaces. However, the asymptotic behavior of the solutions to the three-dimensional Navier-Stokes-Landau-Lifshitz system remains an open problem. Motivated by the study of the decay rates for Navier-Stokes equations, the main purpose of this paper is to study the global existence and decay rates of smooth solutions to the system (1). However, compared with the Navier-Stokes equations, some new difficulties arise due to the additional presence of magnetic moment. Especially, the strong coupling nonlinearities |∇ d|²d and d×Δd in (1c) will cause serious difficulties in the proofs of the time-independent global energy estimates.

For the system (1), the initial data are given by

(2)

and

(3)

for any integer N≥2 with a fixed vector ω₀∈ S², that is, |ω₀|=1. Furthermore, as the spatial variable tends to infinity, we assume

(4)

The main tools in the present paper consist of the higher-order energy estimate and the Fourier splitting method. The paper is organized as follows. In Section 2, we obtain the global solution under the assumption of small initial data with the help of the energy method. In Section 3, we establish the time decay rate of the velocity u and the magnetic moment d. In Section 4, with the previous decay estimates, we combine the Fourier splitting method^[24] with the inductive step^[25-26] to establish time decay rates of the higher-order spatial derivatives of the solution. In Section 5, we establish the time decay rates for the mixed space-time derivatives of velocity and magnetic moment.

Throughout this paper, D^l with an integer l≥0 stands for any spatial derivatives of the order l. When l < 0 or l is not a positive integer, D^l stands for Λ^l defined by , where is the Fourier transform of u, and is its inverse. For any integer s≥0, we use to denote the usual Sobolev spaces with norm ||·||_H^s and L^p(1≤p≤∞) to denote the usual spaces with norm ||·||_L^p. We will use the notation to mean that A≤CB for a universal constant C > 0 that only depends on the parameters coming from the problem and the indexes N and s coming from the regularity on the data. We also use C₀ for a positive constant depending additionally on the initial data. Our main results are stated in the following theorems.

Theorem 1  Assume that the initial data (u₀, d₀-ω₀) satisfy (1)-(4). There exists a constant δ₀ > 0 such that if

(5)

then the problem (1) has a unique global solution (u, d) satisfying that for all t≥ 0,

(6)

Theorem 2  Let (u, d) be the smooth solution obtained in Theorem 1. Assume additionally , for any 1≤ p < ∞ and a unit vector ω₀. Then, there exists a small number δ₀ > 0 such that if

(7)

then

(8)

(9)

Theorem 3  Let (u, d) be the smooth solution obtained in Theorem 1, assume additionally , and assume that

(10)

where C₀=C₀(u₀, d₀, ω₀). Then, for , there exists C_m=C_m(μ, C₀) such that

(11)

and for 2≤p≤∞, there holds

(12)

especially,

(13)

Remark 1  Since (10) is valid for by Theorem 3, under all the assumptions of Theorem 3, we obtain the decay estimates

(14)

(15)

(16)

Moreover, we establish decay rates for the mixed space-time derivatives of solutions to the Cauchy problem (1)-(4).

Theorem 4  Under all the assumptions in Theorem 2, the global classical solution (u, d) of the Cauchy problem (1)-(4) has the time decay rate

(17)

2 Energy estimates

In this subsection, we will derive the a priori energy estimate for the system (1) by assuming that

(18)

for sufficiently small δ > 0.

We first recall the Sobolev interpolation of the Gagliardo-Nirenberg inequality.

Lemma 1  Let 0≤m, and α≤l. Then, we have

(19)

where 0≤θ≤1, and α satisfies

Here, if p=∞, we require that 0 < θ < 1.

Proof  This can be found in Page 125 of Ref. [30].

We recall the following commutator estimates:

Lemma 2  Let m≥1 be an integer and define the commutator

(20)

Then, we have

(21)

In addition, we have that for k≥0,

(22)

where p, p₂, and p₃∈(1, ∞), and

(23)

Proof  Readers can refer to Lemma 3.1 in Ref. [31].

We begin with the first type of energy estimates including u and d.

Lemma 3  If (18) holds, then for k=0, 1, ···, N, we have

(24)

Proof  Applying D^k to (1b), D^k+1 to (1c), and multiplying the resulting identities by D^ku, D^k+1d, respectively, summing up them and then integrating over by parts, we get

(25)

We shall estimate each term on the right hand side of (25). First, for the term I₁, by using Lemma 1 and Lemma 2, we obtain

(26)

For I₂, integrating by parts and employing the Leibniz formula and Hölder's inequality, we obtain

(27)

If , by using Lemma 1, we get

(28)

where α is defined by

Since , we have .

If , by using Lemma 1 again, we get

(29)

where α is defined by

(30)

Since , we have .

Combining (28) and (29), by Cauchy's inequality, we deduce from (27) that for 0≤l≤k,

(31)

And for the term I₃, similarly,

(32)

If , by using Lemma 1, we get

(33)

where α is defined by

(34)

and .

If , by using Lemma 1 again, we get

(35)

where α is defined by (30), and .

Combining (33) and (35), by Cauchy's inequality, we deduce from (32) that for 0≤l≤k,

(36)

By integration by parts, Leibnitz formula, and Hölder's inequality, the fourth term on the right hand side of (25) can be estimated as

(37)

Now, we estimate the first term I₄₁. If , by using Lemma 1, we get

(38)

where α is defined by

Since , we have .

If , by using Lemma 1, we get

(39)

where α is defined by

Since , we have .

Combining (38) and (39), we deduce from (37) that for 0≤ l≤k,

(40)

Similarly, I₄₂ can be estimated as follows:

(41)

The third term on the right hand side of (37) can be estimated by

(42)

Next, we estimate the last term I₄₄. If , by using Lemma 1, we get

(43)

where α is defined by

Since , we have .

If , by using Lemma 1, we get

(44)

where α is defined by

Since , we have .

Combining (40)-(44), we deduce from (37) that

(45)

Finally, it remains to estimate the last term I₅, note that (a×b)· b=0, and we have

(46)

Now, we begin to estimate ||D^ld×D^k-l+2 d||_L². If , by using Lemma 1, we get

(47)

where α is defined by

Since , we have .

If , by using Lemma 1, we get

(48)

where α is defined by

Since , we have

In what follows, we give the estimate of the remaining term . If , by using Lemma 1, we get

(49)

where α is defined by

Since , we have .

If , by using Lemma 1, we get

(50)

where α is defined by

Since , we have .

Combining (47)-(50), we deduce from (46) that for 0≤ l≤k+1,

(51)

Summing up the estimates for I₁~ I₅, i.e., (26), (31), (36), (45), and (51), we deduce (24) for 0≤k≤N, and this yields the desired result.

Next, we derive the second type of energy estimates excluding d-ω₀.

Lemma 4  If (18) holds, then we have

(52)

Proof  Since ω₀ is a unit constant vector, we rewrite 1(c) as

(53)

and multiplying (53) by d-ω₀, integrating by parts, we obtain

(54)

where we have used Hölder's inequality, (18), and (a× b)· b=0.

Thus,

Next, we will combine all the energy estimates that we have derived to prove Theorem 1.

Proof  We first close the energy estimates at each lth level in our weaker sense. Let N≥2 and 1≤m≤N. Summing up the estimates (24) of Lemma 3 from k=0 to k=m, since δ is small, we obtain

(55)

which, together with (52), yields

(56)

Let m=1 in the estimates (56), and we have

(57)

and then integrating directly in the time variable, we get

(58)

By a standard continuity argument, this closes the a priori estimates (18). This in turn allows us to take m=N in (56), and then integrate it directly in the time variable to obtain (6). This completes the whole proof of Theorem 1.

3 Proof of Theorem 2

In this section, we shall give the proof of Theorem 2. In order to establish that d-ω₀ decays in for p > 1, we first establish the following inequality.

Lemma 5  Under the assumption (18), for p≥2, we have

(59)

Proof  Let 2≤p < ∞ and multiply (53) by |d-ω₀|^p-2(d-ω₀), which gives

(60)

We can estimate the second term on the left hand side of (60) by integration by parts as follows:

(61)

The first term on the right hand side of (60) is estimated as

(62)

where we have used (18) and |d|=1.

By virtue of integration by parts and (a×b)· b=0, the second term on the right hand side of (60) is estimated as

(63)

Substituting (61)-(63) into (60), for 2≤p < ∞, we reach the desired estimate (59).

Lemma 6  Under the assumption (18), and , we have

(64)

Proof  Multiply (53) by (or alternatively by , and ε→0), which gives

(65)

The first term on the right hand side of (65) can be estimated by integrating by parts as

(66)

The second term on the right hand side of (65) can be estimated by using |d|=1 as

(67)

The third term on the right hand side of (65) can be estimated by integrating by parts and using (a×b)· b=0 as

(68)

Combining (66)-(68), we deduce from (65) that

(69)

Integrating the inequality (69) with respect to t yields

(70)

Similar to (70), we have from (52) that

(71)

Combining the inequalities (70) and (71) yields

This completes the proof of the lemma.

Lemma 7  Let d be the solution obtained in Theorem 1. Assume , 1≤p < ∞. Then, we have

(72)

Proof  According to the idea in Ref. [32], we multiply (59) by (1+t)^α, for an arbitrary α > 0, which yields

(73)

With Hölder's inequality, the right hand side of (73) is estimated as

(74)

where , and α > γp.

Substituting the estimate (74) into (73) and taking ε > 0 suitably small, we have

(75)

where we use Lemma 6.

Integrating the inequality (75) with respect to t yields

(76)

from which it follows

(77)

Due to α > γp,

(78)

This completes the proof of the case p≥2. For the case 1≤ p < 2, applying the interpolation inequality (78) and Lemma 6 yields

(79)

This completes the proof of the lemma.

Next, we turn to establish L² decay of the velocity u.

Lemma 8  Let (u, d) be the solution obtained in Theorem 1. Assume that the initial data satisfy Theorem 2. Then, we have

(80)

Proof  Multiplying (1b) and (53) by u and d-ω₀, respectively, summing up them, and then integrating over by parts, we get

(81)

The first integral on the right hand side of (81) is estimated as

(82)

where we use (6) and (18).

By Hölder's inequality, the second integral on the right hand side of (81) is estimated as

(83)

By integrating by parts and using (a×b)· b=0, the last integral on the right hand side of (81) is estimated as

(84)

Substituting the estimates (82)-(84) into (81), we have

(85)

Applying Plancherel's theorem to (85) gives

(86)

As in Ref. [26], we define the ball

for a constant k that will be specified as below. Hence,

(87)

where S(t)^c is the complementary set of S(t). Then,

(88)

Here, we have used the decay estimate which has been obtained in Lemma 7 with p=2. The following estimate, which will be established later, is needed:

(89)

for an absolute constant C. Then, we obtain

(90)

Combining the inequalities (88) and (90) yields

(91)

Multiplying both sides of (91) by (1+t)^Ck, we get

(92)

where .

Solving the inequality directly yields

(93)

To complete the proof, we need to establish the inequality (89). As in Ref. [33], taking the Fourier transform in the system (1b) yields

(94)

where

(95)

and indicates the Fourier transform. Multiplying (94) by the integrating factor e^|ξ|2t yields

Integrating in the time variable gives

(96)

We analyze each term in G(ξ, t) separately. We have

(97)

Similarly, we see

(98)

Taking the divergence of the velocity equation in the system (1) yields

(99)

Taking the Fourier transform gives

(100)

It follows that , and thus

(101)

Substituting (97), (98), and (101) into (96), for ξ∈ S(t), we get

(102)

Then, we obtain

(103)

Substituting (103) into (88), we get

(104)

Similarly, multiplying both sides of (104) by (1+t)^Ck, we get

where .

Solving the inequality directly yields

(105)

Due to (105), (97) is estimated as

(106)

Using Lemma 7 gives

Then,

(107)

and . Hence,

(108)

Combining (106)-(108) and (95) yields

(109)

Substituting (109) into (96), for ξ∈ S(t), we get

(110)

since . It completes the proof of (89) and hence completes the proof of the lemma.

Proof of Theorem 2  Combining Lemma 7 and Lemma 8 yields Theorem 2.

4 Proof of Theorem 3

In order to establish Theorem 3, we first establish a higher-order energy estimate for the solution.

Lemma 9  Let (u, d) be the solution obtained in Theorem 1, and assume additionally and . Then, for , we have the following inequality:

(111)

where

(112)

with , and .

Proof  As in Ref. [26], applying D^m to (1b), and multiplying by D^mu, integrating by parts, we obtain the following inequalities:

(113)

For the third term on the right hand side of (113), by the Gagliardo-Nirenberg inequality, Theorem 1 and Theorem 2, for m≥2, we obtain

(114)

By the Gagliardo-Nirenberg inequality, the fifth term on the right hand side of (113) is estimated as

(115)

Moreover, the last integral on the right hand side of (113) is estimated as

(116)

Applying D^m to (1c), multiplying by D^md, and integrating by parts, we obtain the following inequalities:

(117)

By the Gagliardo-Nirenberg inequality, the second term on the right hand side of (117) is estimated as

(118)

The third integral on the right hand side of (117) is estimated as

(119)

The last integral on the right hand side of (117) is estimated as

(120)

This completes the proof of the lemma for m≥3. Next, we consider the cases m=1 and 2. If m=1, then

(121)

(122)

(123)

(124)

(125)

For the case m=2, we have

(126)

(127)

in which

where we have used Theorem 1 and (18). Moreover,

(128)

(129)

(130)

This completes the proof of the lemma for m = 1 and 2.

We now establish the following auxiliary lemma which follows the idea in Ref. [26].

Lemma 10  Let , assume

(131)

and suppose

(132)

with s_i≥ ρ_m-1+2. Then,

(133)

with ρ_m=1+ρ_m-1, where C_m=C_m (C_m-1, C_i, s_i, ρ_m-1, m).

Proof  We use the Fourier-splitting argument. Let

Then,

Using the last inequality and the hypothesis (132), we have

Multiplying (t +1)^k, integrating in the time variable and dividing by (t +1)^k, we get

Since s_i≥ ρ_m-1+2, the conclusion of the lemma follows.

We are now ready to prove Theorem 3.

Proof of Theorem 3  We first consider the cases m = 1 and 2. By the Gagliardo-Nirenberg inequality, Theorem 1, and Theorem 2, we have

(134)

for m≥2.

Similarly,

(135)

(136)

(137)

for k≥3.

Substituting (134)-(137) into (112), we obtain

(138)

Therefore, the result holds for m = 1 and 2. We can now use Lemma 10 directly to obtain (11). For m≥3, we need to estimate R_m of (112),

(139)

where , and note that since , we have ki≥2μ+(m+1). , and note that since , we have ei≥2μ+(m+1). ri=2μ+, and note that since 1≤i≤m-1, we have ri≥2μ+(m+1). , and note that since , we have wi≥2μ+(m+1). , and note that since , we have xi≥2μ+(m+1). , and note that since , we have yi≥2μ+(m+1). , and note that since , we have zi≥2μ+(m+1). Moreover, we use the induction hypothesis ||Dk(u, d-ω0)||L22≤C(t+1)-k for k≤ m-1.

Substituting (139) into (111), we obtain the hypothesis (132). Applying Lemma 10 directly, we obtain the conclusion (11) for m≥3.

As for (12), by the Gagliardo-Nirenberg inequality,

and (13) follows by interpolating the above inequality.

5 Proof of Theorem 4

In this section, we will establish the time decay rates for the mixed space-time derivatives of velocity and magnetic moment.

Proof of Theorem 4  First of all, we shall estimate ||∇^l∂_tu||_L². Applying D^l to (1b), multiplying the resulting identities by D^l∂_tu, integrating the resulting equation over , and using Young's inequality, one gets

(140)

By using Lemma 2 and Theorem 3, we estimate the first factor in the inequalities (140),

(141)

Similar to the estimate of the term J₁, for the terms J₂ and J₃, we have

(142)

(143)

Combining (141)-(143), we deduce from (140) that

(144)

Similar to the estimate of the term ||D^l∂_tu||_L², applying D^l to (1c), multiplying the resulting identities by D^l∂_td, integrating the resulting equation over , and using Young's inequality, one gets

(145)

Similar to the estimate of the terms J₁ and J₂, we easily estimate

(146)

(147)

By employing the Leibniz formula, Hölder's inequality, Young's inequality, and Lemma 1, H₃ is estimated as follows:

(148)

Similarly, we have

(149)

Combining (146)-(149), we deduce from (145) that

(150)

Then, we complete the proof of Theorem 4.

Acknowledgements We would like to express our sincere thanks to Academician Boling GUO of Institute of Applied Physics and Computational Mathematics in Beijing for his fruitful help and discussion.