Shanghai University
Article Information
- C. Q. RU
- A simple criterion for finite time stability with application to impacted buckling of elastic columns
- Applied Mathematics and Mechanics (English Edition), 2018, 39(3): 305-316.
- http://dx.doi.org/10.1007/s10483-018-2311-9
Article History
- Received Sep. 18, 2017
- Revised Sep. 19, 2017
Stability theories of dynamic systems (e.g., mechanical systems) are largely based on the concepts and analytical methods of Liapunov stability which, for example, can be used to determine a critical value of the loading parameter by examining asymptotic behavior of the system to infinitesimal disturbances when time approaches infinity (t → ∞). However, for many practical problems such as impacted buckling of elastic columns, the duration of response tf, determined by the loading and other parameters, can be extremely short and then makes it meaningless to examine asymptotic behavior of the system when t→ ∞. For example, for an impacted elastic column, the duration of response tf can be much shorter than its first period of free vibration. For such extremely short duration of response, experiments have showed that elastic structures can sustain an impact load of huge magnitude many times higher than the linearized critical value, without losing their linearized stability. Therefore, it is of great practical and theoretical significance to study finite time stability of dynamic systems [1-4].
The existing theories of "finite time stability"[1-4] define a dynamic system to be finite-time stable if its response to initial disturbances bounded by a given bound does not exceed a given threshold during a given time interval. Unlike the existing finite-time stability theories, it is well known that the classical stability criteria (e.g., the static Euler-criterion or the Liapunov dynamic criterion) can determine an objective critical value for stability observed in experiments without artificially specifying any prescribed bound or prescribed threshold. For example, for the classical problem of an elastic column under a constant compressive force, a critical value of the compressive force can be determined uniquely for arbitrary infinitesimal disturbances, by a static criterion or the Liapunov dynamic criterion, without specifying any prescribed threshold for allowable deflections. Indeed, for many practical problems, one real difficulty of the existing finite-time stability theories[1-4] is how to specify the prescribed bound on initial disturbances and the prescribed threshold for allowable responses for finite time instability observed in real experiments.
For impacted buckling of elastic/plastic structures during a short time interval, for instance, a common practice is to use the concept of "amplification factor" (defined by the growth rate of an initial disturbance from t=0 to t=tf)[5-7], and the critical value of the impact load is defined based on a specified value (say, 10, 50, or 100) of amplification factor. However, this specified value of amplification factor can vary for different cases, and how to specify this prescribed value of amplification factor for various elastic structures under different loading conditions remains a non-trivial challenge.
In the literature on impacted buckling of elastic/plastic structures, a more specific criterion developed by Budiansky and co-workers has been widely used by many researchers[7-11]. This criterion is based on a response-curve which shows the dependence of the system's response (e.g., defined by the maximum deflection) on the applied load (such as the impact loading). The critical value of the applied load is expected to be estimated by identifying a point at which a small increase of the applied load causes a significant increase of the system's response. Practically, however, because the response-curve is usually a smooth curve without any special point characterized by a catastrophic change, it is a "non-trivial" task[9-11] to identify a specific point as the critical point. Therefore, it is safe to conclude that for finite-time stability in general and for impacted buckling of elastic structures in particular, it remains an open question how to identify the critical value of the loading parameter for instability or buckling observed in real experiments, without the need of specifying any prescribed threshold for allowable responses.
The present work is motivated by an attempt to develop a simple criterion for finite time stability which can be used to estimate the critical value of the loading parameter for instability observed in experiments without the need of specifying any prescribed threshold for allowable responses. To this end, an energy-based simple criterion is proposed for finite time stability of a linear dynamic system with constant coefficients. The derived criterion is challenged by comparing its predictions with available experimental and simulation data for several typical problems of impacted buckling of elastic columns. As will be shown below, the simple formulas given by the proposed criterion are in robust reasonable agreement with available experimental and simulation data for several impacted buckling problems of elastic columns, which offers a justification of the usefulness and reasonable accuracy of the proposed criterion for finite time stability.
2 An energy-based criterion for finite time stabilityLet us study stability of a known dominate state (e.g., an equilibrium point) of a dynamic system against infinitesimal random disturbances during a given finite time interval [0, tf]. Unlike most existing methods on finite time stability [1-4] or impacted buckling of elastic structures[10-26] which focused on detailed time-varying solutions of the governing equation in the given time interval [0, tf], we shall focus on the overall energy balance relation given by the integral of the governing equation over the time interval [0, tf]. Our basic idea is that, if for all possible deviations of the system from the dominate state, the energy absorbed and dissipated by the system exceeds the work done by the loading force on the deviation, then no deviation can actually happen and thus the dominate state is stable. Here, the deviations should be characterized by two conditions: (ⅰ) all initial values of disturbance's energy at t=0 are negligible; and (ⅱ) the initial values of all deviations at t=0 are negligible as compared with their final values at t=tf.
To illustrate the idea and related analysis, let us consider finite time stability of an equilibrium point (y=0) of a simple dynamic system whose deviations from the equilibrium point are governed by the equation with constant coefficients (μ, k),

|
(1) |
where the μ-term represents the damping effect, k2 (>0) is the driving force for instability, and g(t) is an arbitrary infinitesimal random disturbance force whose network on any deviation over the time interval [0, tf] is negligible,

|
(2) |
The homogeneous equation of (1) has two real eigenroots (p1, -p2) of opposite signs, where

|
(3) |
Thus, the deviation y(t) is of the form

|
(4) |
where y(tf)≈ y0(tf)≈ Aep1tf, A and B are two constants determined by initial infinitesimal disturbances, and the particular solution yp(t) can be constructed, independent of the initial disturbances, by the method of "variation of parameters" with the chosen end conditions u(tf)=0 and v(0)=0 as follows:

|
(5) |
Thus, a sufficient condition for stability of the equilibrium state (y=0) against all possible deviations is that the energy absorbed and dissipated by the system exceeds the work done by the loading force on the deviation, as given by the energy inequality,

|
(6) |
In view of the two characteristics of all deviations described above, conditions (2), (4), (5) and

|
and also the inequality

|
(7) |
the above sufficient condition (6) for stability becomes

|
It follows from the eigen-equation (3) that a sufficient condition for finite-time stability of the equilibrium state (y=0) in the given time interval [0, tf] is given, in terms of the maximum eigen-root p1, by

|
(8) |
In particular, in the absence of damping (μ =0) and then the maximum eigenroot p1=k, this condition (8) indicates that the critical value of the loading parameter (k2) for stability is inversely proportional to the squared duration (tf)2

|
(9) |
In summary, for a linear dynamic system governed by an equation with constant coefficients, a simple sufficient condition for finite time stability during a given time interval [0, tf] is that the product of the maximum growth rate (given by the maximum eigen-root p1>0) and the duration tf does not exceed 2, i.e., p1tf < 2. The corresponding criterion (p1tf=2) is equivalent to a specific amplification factor e2 defined based on specific initial disturbances so that y(t)~ ep1t. In this sense, the proposed criterion (p1tf=2) endows the amplification factor (e2) with physical relevance for the instability observed in experiments. In what follows, we shall challenge this simple criterion (p1tf=2) by comparing its predictions with available experimental and simulation data for several problems of impacted buckling of elastic columns.
3 Finite time dynamic buckling of an axially-compressed elastic columnLet us study finite time stability of a hinged axially compressed elastic column of length L under a constant axial compressive force P higher than the static Euler critical value PE during a finite time interval [0, tf]. The dynamic bucking deflection is governed by

|
(10) |
where x is the axial coordinate, t is time, w(x, t) is the bending deflection, I and A are the moment of inertia and the area of the cross-section, respectively, and E and ρ are Young's modulus and the mass density (per unit volume), respectively. With the buckling mode

|
where n=1, 2, ..., (10) gives

|
(11) |
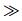
First, when the axial force is much higher than the static Euler critical value, then P 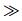

|
(12) |
and the associated maximum growth rate is given by

|
(13) |
Thus, the criterion (8) gives the critical condition for finite-time stability of a hinged column within the time interval [0, tf], under the condition (n2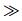
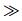

|
(14) |
It is stated that for given material and cross-section parameters (I, A, E, ρ), the critical force is inversely proportional to the duration tf and independent of the column length L. Here, it is noticed that for a hinged beam under a constant axial force P 
In addition, for a hinged column, the first natural frequency and the corresponding first period are

|
Thus, the critical force Pcr given by (14) can be written as

|
(15) |
It is concluded that when P
If the compressive force P is just moderately higher than PE (say, PE < P < 5PE, then roughly, the integer n≈ 1 in (12)), the maximum growth rate is associated with the first mode (n=1) (see, e.g., the "Hoff problem"[14-18] to be discussed below), and the governing (11) and the associated maximum growth rate are given by

|
(16) |
Thus, the critical condition (p1tf=2) for finite-time stability (with n=1) is

|
(17) |
It is noticed that, unlike the formula (14), the critical force given by (17) is dependent on the column length L.
Here, it should be stressed that the critical force formulas (14) and (17) are derived for a hinged column. For other end conditions, the critical force will be different from that estimated by (14) and (17). However, in the case P 
Now, let us challenge the simple criterion (p1tf=2) and the derived formulas (14) and (17) by comparing their predictions with available experimental and simulation data of some problems of impacted buckling of elastic columns. In these cases, the axial force P(t) is of the form of a half-sine wave (Subsections 4.1 and 4.2) or a linear function of time t (Subsection 4.3), and will be replaced by its average value over the time duration.
4.1 An elastic column longitudinally impacted by a mass M with a speed VFirst, let us consider the buckling problem of an elastic column impacted by a mass M with a high speed V[5-7, 10-11, 19-24]. If the axial inertia of elastic column is ignored[5-7, 14-19], and the elastic column is treated as a spring of the spring constant 

|
and the impact duration tf (determined when the spring force reduces to zero at t=tf and then the mass M loses contact with the column) and the axial compressive force F(t) can be estimated by

|
(18) |
In particular, the axial force F(t) is of the form of a half since wave[11], and the time-average axial force in the duration [0, tf] is estimated by

|
(19) |
The simple estimates (18) and (19) can be verified with reasonable accuracy by some available numerical data. For example, it is readily verified that the value of a dimensionless time defined by Ari-Gur et al.[10] (see "τ" defined by (2.4)) estimated by our formula (18) is 3.0 and 161, respectively, for the two cases of a light and a huge striking mass, (ⅰ) M=175 g, m=ALρ = 47 g and (ⅱ) M=492 kg, m=47 g, in very good agreement with their numerical data 2.6 and 160 (see Ref. [10], p.633, p.639).
Thus, for a hinged elastic column longitudinally impacted by a mass M with a speed V, under the condition (which means that Faverage

|
(20) |
the critical condition is obtained from (14), (18), and (19) as

|
(21) |
To the best of our knowledge, in spite of extensive researches on this problem, no similar formula is available in the existing literature[10-26]. In particular, our formula (21) predicts that the critical condition for impacted buckling is determined by linear momentum (VM) rather than kinetic energy (MV2/2) of the striking mass. In addition, under the condition (Faverage
Let us now compare the critical speed predicted by our formula (21) with the available experimental data. Unfortunately, the test results of Ari-Gur et al.[10] are the only one we have identified in the literature which gave clear experimental data on the critical speed, but for a doubly-clamped column (see Tables 1 and 2 of Ref. [10]). Listed in Table 1 is a comparison for those specimens tested in Ref. [10] which meet the condition (Faverage=10-30PE). It is seen that the critical speed given by our formula (21) is slightly, but consistently, lower than the test data of Ref. [10], with a relative error between 25%-40%. As explained previously, in the case (Faverage=10-30PE), because the critical force is associated with a higher-order mode (n=2, 3, 4), the relative error between a hinged and a doubly-clamped column decays quickly and monotonically with the increasing mode number n≥ 1 (for instance, the relative error in the natural frequency is about 125% for n=1, but quickly reduces to 35% for n=3). Therefore, the critical speed for a doubly-clamped column tested in Ref. [10] is expected to be only moderately (say 35% for n=3) higher than that given by (21) derived for a hinged column. It is reasonable to conclude that the formula (21) is in reasonably good agreement with the experimental data of Ref. [10]. In addition, it is easily verified that the required condition (20) is well met for all specimens collected in Table 1. Actually, the left side is more than two orders of magnitude larger than the right side of (20) for all listed specimens.

|
Another important problem is longitudinal impact of an elastic column on a rigid wall. Let the flight speed of the column before impact be V, and the axial force on the impacted end (x=L) be F(t). Because the axial force at free end (x=0) is zero, it is assumed that the axial force (axial strain) is linearly distributed along the column, and thus the axial displacement u(x, t) is of the form

|
In addition, because u(L, t)=0 at the impacted end (x=L) during the impact interval [0, tf], we have (where um is the displacement of the mass center x=L/2 of the column)

|
Thus, the dynamic equation for the mass center um(t) of the column is

|
(22) |
and it follows from the initial conditions that

|
(23) |
and

|
Thus, the average axial force at the impacted end (x=L) during the time interval [0, tf] is estimated by

|
(24) |
The above estimated values of the duration tf (23) and the average force (24) at the impacted end are in good agreement (with relative error less than 5%) with the following known results derived by other more complicated analysis or numerical simulations (see Davidson[19], also Wang et al.[27], see their Fig. 2 where a rigid wall can be approximated by an extremely stiff spring with the dimensionless spring constant equal to 100):

|
(25) |
Based on the above formulas (23) and (24), the critical condition for impact buckling of a hinged elastic column with a speed V on a rigid wall is given by

|
(26) |
which has a similar form as the formula (21). In particular, the condition (Fimpacted-end 

|
(27) |
Unfortunately, detailed comparison of the present formula (26) with any test data cannot be made here due to the lack of available experimental data.
4.3 An elastic column compressed at a constant speed v0 (Hoff problem)Finally, let us consider the so-called "Hoff problem" of an elastic column axially compressed at a constant speed v0 over a time interval [0, tf]. Again, with ignored axial inertia[14-18], the column is uniformly compressed with the axial strain (v0t/L) and the axial compressive force P(t)=(AEv0t/L). Since the duration of instability development is accounted from the instant t0(< tf) at which P(t)=PE and after then P(t)>PE, the effective time duration tf* for instability development is tf-t0 given by

|
(28) |
The average value of the axial compressive force over the time interval [t0, tf] is

|
(29) |
Since almost all existing works on the Hoff problem[14-18] have followed Hoff's original assumption and adopted the first mode (n=1) as stated in Section 3, we should confine our discussion to the case when P is just moderately higher than PE, say, PE < Paverage < 5PE or PE < P(tf) < 9PE. With this restriction, the critical condition (17) for finite-time stability over the given time interval gives

|
which leads to the following critical condition, in terms of the dimensionless time τ and the dimensionless loading parameter Ω:

|
(30) |
Thus, (30) can be used to estimate the critical value of compression speed v0 for a given duration tf, or to estimate the critical time tf when the compression speed v0 is given. In particular, the axial force at the critical instant (t=tf), as a function of the dimensionless loading parameter Ω, is given by

|
(31) |
For example, the dependence of dimensionless critical force Pcr/PE given by (31) on the dimensionless loading parameter Ω is shown in Table 2. It is seen that the ratio Pcr/PE is beyond the restriction (PE < P(tf) < 9PE) for Ω below 0.01. Therefore, our comparison will be limited to the cases Ω≥ 0.01.
It is well-known that a compressed column has stable post-buckling behavior and can support a maximum axial force considerably higher than the linearized critical value. Since the present critical conditions (8), (14), (30), and (31) are all based on a linearized stability analysis and considered as the linearized critical value, the critical value Pcr/PE given by (31) should be compared with the force at the first bifurcation point of buckling deflection. Here, due to a lack of such relevant data in Refs. [14]-[18], we give a qualitative comparison of the formula (31) with the force at the first peak for a hinged column with an initial imperfection, as those shown in Fig. 5 of Ref. [16], and Fig. 2 of Ref. [17] (where (Vb*)2=1/Ω defined by (30)). Listed in Table 3 is such a comparison of the critical force Pcr/PE given by (31) with the mentioned data given in Refs. [16] and [17]. It is seen from Table 3 that the present formula (31) is in reasonable agreement with Refs. [16] and [17], in spite of a few rude simplifications made in our analysis for formulas (30) and (31), and the initial imperfection assumed in Refs. [16] and [17] could be responsible for the fact that the data shown in Refs. [16] and [17] are relatively lower than those given by (31). More careful comparison of the present formulas (30) and (31) with known data of the Hoff problem cannot be made here due to the lack of available data.
A simple criterion is developed for finite time stability of dynamic system against infinitesimal disturbances, which can be used to estimate the critical value of loading parameter for the instability observed in experiments without the need of specifying a prescribed threshold for allowable responses. The original form of the proposed criterion is derived for dynamic systems governed by a linear equation with constant coefficients, and can be used for time-varying linear systems when the time-dependent loading parameter can be replaced approximately by its average value over the time duration. Our main results are summarized as follows.
(ⅰ) A sufficient condition is developed which indicates that finite time stability of a linear dynamic system with constant coefficients during a given time interval [0, tf] is guaranteed provided the product of the maximum eigen-root p1 and the duration tf does not exceed 2, i.e., p1tf < 2.
(ⅱ) Based on the proposed criterion (p1tf=2), simple formulas for critical parameters are derived for three problems of impacted buckling of elastic columns: an elastic column impacted by a striking mass, longitudinal impact of an elastic column on a rigid wall, and an elastic column compressed at a constant speed ("Hoff problem"), in which the time-varying loading parameter is replaced by its average value over the time interval.
(ⅲ) The critical parameters predicted by our formulas for impacted buckling of elastic columns are in reasonably good agreement with available experimental and simulation data, which suggests that the proposed criterion (p1tf=2) could be used to estimate the critical parameter for finite time stability of dynamic systems.
| [1] | Dorato, P. An overview of finite time stability. Current Trends in Nonlinear Systems and Control (ed. Menini, L. ), Springer, Boston, 185-194(2006) |
| [2] | Bhat, S. P. and Bernstein, D. S. Finite time stability of continuous autonomous systems. SIAM Journal on Control and Optimization, 38, 751-766 (2000) doi:10.1137/S0363012997321358 |
| [3] | Amato, F., de Tommasi, G., and Pironti, A. Necessary and sufficient conditions for finite-time stability of impulsive dynamics linear systems. Automatica, 49, 2546-2550 (2013) doi:10.1016/j.automatica.2013.04.004 |
| [4] | Kussaba, H. T. M., Borges, R. A., and Ishihara, J. Y. A new condition for finite time boundedness analysis. Journal of the Franklin Institute, 352, 5514-5528 (2015) doi:10.1016/j.jfranklin.2015.09.005 |
| [5] | Lindburg, H. E. Impact buckling of a thin bar. Journal of Applied Mechanics, 32, 315-322 (1965) doi:10.1115/1.3625801 |
| [6] | Abrahamson, G. R. and Goodier, J. N. Dynamic flextual buckling of rods within an axial plastic compression wave. Journal of Applied Mechanics, 33, 241-248 (1966) doi:10.1115/1.3625033 |
| [7] | Lindburg, H. E. Little Book of Dynamic Buckling, LCE Science/Software (2003) |
| [8] | Hutchinson, J. W. and Budiansky, B. Dynamic buckling estimates. AIAA Journal, 4, 525-530 (1966) doi:10.2514/3.3468 |
| [9] | Simitses, G. J. Instability of dynamically-loaded structures. Applied Mechanics Reviews, 40, 1403-1408 (1987) doi:10.1115/1.3149542 |
| [10] | Ari-Gur, J., Weller, T., and Singer, J. Experimental and theoretical studies of columns under axial impact. International Journal of Solids and Structures, 18, 619-641 (1982) doi:10.1016/0020-7683(82)90044-0 |
| [11] | Weller, T., Abramovich, H., and Yaffe, R. Dynamic buckling of beams and plates subjected to axial impact. Computers and Structures, 32, 835-851 (1989) doi:10.1016/0045-7949(89)90368-4 |
| [12] | Kornev, V. M. Development of dynamic forms of stability loss of elastic systems under intensive loading over a finite time interval. Journal of Applied Mechanics and Technical Physics, 13, 536-541 (1972) |
| [13] | Morozov, N. F., Il'in, D. N., and Belyaev, A. K. Dynamic buckling of rod under axial jump loading. Doklady Physics, 58, 191-195 (2013) doi:10.1134/S1028335813050078 |
| [14] | Hoff, N. J. The dynamics of the buckling of elastic columns. Journal of Applied Mechanics, 18, 68-74 (1951) |
| [15] | Elishakoff, I. Hoff's problem in probabilistic setting. Journal of Applied Mechanics, 47, 403-408 (1980) doi:10.1115/1.3153677 |
| [16] | Kounadis, A. N. and Mallis, J. Dynamic stability of initially crooked columns under a timedependent axial displacement of their support. Quarterly Journal of Mechanics and Applied Mathematics, 41, 579-596 (1988) doi:10.1093/qjmam/41.4.579 |
| [17] | Motamarri, P. and Suryanarayan, S. Unified analytical solution for dynamic elastic buckling of beams for various boundary conditions and loading rates. International Journal of Mechanical Sciences, 56, 60-69 (2012) doi:10.1016/j.ijmecsci.2012.01.003 |
| [18] | Kuzkin, V. A. and Dannert, M. M. Buckling of a column under a constant speed compression:a dynamic correction to the Euler formula. Acta Mechanica, 227, 1645-1652 (2016) doi:10.1007/s00707-016-1586-5 |
| [19] | Davidson, J. F. Buckling of struts under dynamic loading. Journal of the Mechanics and Physics of Solids, 2, 54-66 (1953) doi:10.1016/0022-5096(53)90027-1 |
| [20] | Zhang, Z. and Taheri, F. Dynamic pulse-buckling behavior of quasi-ductile carbon/epoxy and e-glass/epoxy laminated composite beams. Composites and Structures, 64, 269-274 (2004) doi:10.1016/j.compstruct.2003.08.008 |
| [21] | Ji, W. and Waas, A. M. Dynamic bifurcation buckling of an impacted column. International Journal of Engineering Science, 46, 958-967 (2008) doi:10.1016/j.ijengsci.2008.04.003 |
| [22] | Wang, A. and Tian, W. Mechanism of buckling development in elastic bars subjected to axial impact. International Journal of Impact Engineering, 34, 232-252 (2007) doi:10.1016/j.ijimpeng.2005.07.005 |
| [23] | Gladden, J. R., Handzy, N. Z., Belmonte, A., and Villemaux, E. Dynamic buckling and fragmentation in brittle rods. Physical Review Letters, 94, 035503 (2005) doi:10.1103/PhysRevLett.94.035503 |
| [24] | Jiao, X. J. and Ma, J. M. Influence of the connection condition on the dynamic buckling of longitudinal impact for an elastic rod. Acta Mechanica Solida Sinica, 30, 291-298 (2017) doi:10.1016/j.camss.2017.05.003 |
| [25] | Dost, S. and Glockner, P. G. On the dynamic stability of viscoelastic prefect column. International Journal of Solids and Structures, 18, 587-596 (1982) doi:10.1016/0020-7683(82)90041-5 |
| [26] | Giofgi, C., Pata, V., and Vuk, E. On the extensible viscoelastic beam. Nonlinearity, 21, 713-733 (2008) doi:10.1088/0951-7715/21/4/004 |
| [27] | Wang, S., Wang, Y., Huang, Z. L., and Yu, T. X. Dynamic behavior of elastic bars and beams impinging on ideal springs. Journal of Applied Mechanics, 83, 031002 (2016) |
 2018, Vol. 39
2018, Vol. 39




