Nomenclature
1 Introduction Peristaltic activity is quite significant in physiological and industrial processes. Literature is abundant for peristalsis in a planar channel[1-14]. Some attempts for peristaltic activity in a curved channel are recently constructed[15-18]. Peristalsis with heat transfer has utility in acquiring the flow rate of blood through the initial thermal conditions and the thermal clearance rate. This concept is useful in hyperthermia, laser therapy, cancer therapy, oxygenation, hemodialysis etc. Moreover, a heat transfer analysis is important in material processing operations including high temperature plasmas, glass fabrication, and liquid metal fluids. Investigations characterizing peristalsis with heat transfer can be seen in Refs.[19]-[24]. Peristalsis subject to wall properties is useful in arterial blood flows, urine flows in the urethras and air flows in lungs. The wall properties decompose the pressure as stiffness, rigidity and damping whose intensity bears serious impacts on the blood pressure in the human body. The studies[25-28] are relevant in this direction.
The diverse characteristics of non-Newtonian materials are classified by different constitutive relations. Since non-Newtonian models include different perspectives such as viscoelastic, viscoplastic and micro-continuum behaviors, several dynamical mechanisms have been proposed for a better understanding. The Sisko fluid is one of generalized non-Newtonian fluids that is capable to predict rheology of blood, particle disposition in the respiratory tract and diffusion of proteins through its shear thinning-thickening characteristics. However, few studies have been conducted about Sisko fluids yet in the existing literature (see Refs.[20]-[32]).
The variable viscosity such as temperature or radial dependent is an important subclass of rheological liquids when the physical properties of fluids may change considerably with the radius and temperature. However, all of the mentioned citations include the constant fluid viscosity. In lubricating fluid systems, the heat produced by inner friction affects the viscosity of fluid, and thus the constant fluid viscosity consideration is not adequate. Also, in body organs such as lymphatic vessels, intestines, ductus afferents, and small blood vessels, the fluid viscosity varies with the thickness of the tube. Therefore, for the accurate flow behavior, the viscosity variation is permissible. Bhatti et al.[33] presented a study for the heat transfer analysis on the peristaltically induced motion with the variable viscosity. Hayat et al.[34] discussed the variable viscosity on peristalsis of copper-water nanomaterial. Peristalsis of Jeffrey fluid with the non-constant viscosity and nanoparticles has been examined by Alvi et al.[35]. Latif et al.[36] explored peristalsis of magnetohydrodynamic (MHD) third-order fluid with variable properties. Hayat et al.[37] explored variable viscosity effects in a tapered asymmetric channel.
Variations of the viscosity are found essential in lubricating systems, lymphatic vessels, intestines, ductus afferents, and small blood vessels, and thus the constant viscosity is not adequate to study such flow systems. Further, the arterial and intestinal peristalsis occurs in a curved configuration with an important feature of wall compliance (stiffness, rigidity, and elasticity). Thus, the present communication predicts the radially varying viscosity on peristalsis of Sisko fluids. Curvature and compliant characteristics of channel walls are considered. The heat transfer analysis is performed. The viscous dissipation predicts the conversion of kinetic energy of the flow to heat energy. The corresponding system is solved for the long wavelength and small Reynolds number. Such consideration perceives its importance in the field of medicine, biomedicine, and blood flow in micro/nano channels. Solutions with perturbation and numerical approaches are constructed. The main outcomes are discussed in detail with graphs.
2 Problem formulation Here, we develop a mathematical description of Sisko liquids in a curved channel of the inner radius R* and separation 2d. The fluid flow is along the radial direction r, where x is transverse to it. The peristaltic wave travelling radially along the channel boundary causes the fluid to flow initially in the radial direction. In addition, effects of pressure are active in terms of wall's compliant characteristics. The mathematical expression for the considered geometry is given as below,

|
(1) |
where the above symbols represent the peristaltic wave speed c, the amplitude  , the wavelength λ, the time t, and the radial displacements ±
η, respectively.
, the wavelength λ, the time t, and the radial displacements ±
η, respectively.
The above system involves conservation principles of mass, momentum, and energy. Thus, we have continuity, momentum, and energy equations in the following forms:

|
(2) |

|
(3) |

|
(4) |

|
(5) |
where the Cauchy stress tensor τ and the extra stress tensor S for the Sisko fluid model can be written as[1-3]

|
(6) |

|
(7) |
with the first Rivlin-Erickson tensor A1=grad V+grad VT, the second invariant of symmetric part of velocity gradient  , the gradient square
, the gradient square 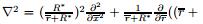
 , the material time derivative
, the material time derivative  , the velocity in the radial and axial directions
, the velocity in the radial and axial directions  the specific heat parameter cp, the pressure p, the fluid density ρ, the thermal conductivity k1, the temperature at the left and right channel walls T0, the temperature of fluid T, and the stress components
the specific heat parameter cp, the pressure p, the fluid density ρ, the thermal conductivity k1, the temperature at the left and right channel walls T0, the temperature of fluid T, and the stress components  . In addition, the parameters a, b, and n (≥0) represent the shear rate viscosity, consistency index, and power-law index for Sisko fluids, respectively. Specifically, the power index n appears to provide an edge to Sisko fluids in predicting shear thinning (n < 1) and shear thickening (n>1) attributes. Also, the Newtonian fluid behavior can be recovered correctly using the specified values of involving parameters (n=1, a=0, b=μ or b=0, and a=μ).
. In addition, the parameters a, b, and n (≥0) represent the shear rate viscosity, consistency index, and power-law index for Sisko fluids, respectively. Specifically, the power index n appears to provide an edge to Sisko fluids in predicting shear thinning (n < 1) and shear thickening (n>1) attributes. Also, the Newtonian fluid behavior can be recovered correctly using the specified values of involving parameters (n=1, a=0, b=μ or b=0, and a=μ).
The curved boundaries of the channel are set to no-slip, prescribed surface temperature and the compliant properties of wall as follows:

|
(8) |

|
(9) |

|
(10) |
where τ*, m1, and d' demonstrate the pressure decomposition as the coefficient of elastic tension in the membrane, the mass per unit area, and the viscous damping, respectively.
The concept of long wavelength perceives special relevance in intestinal peristalsis for chyme movement, blood vessels to avoid bending rigidity of vessel and laser treatment. Thus, making use of the following non-dimensional quantities:

|
(11) |
we have in terms of the stream function ψ(r, x, t)the following systems:

|
(12) |

|
(13) |

|
(14) |

|
(15) |

|
(16) |

|
(17) |

|
(18) |
where the above symbols represent the wave number δ, the amplitude ratio parameter  , the Reynolds number Re, the Prandtl number Pr, the elasticity parameters Ei(i=1, 2, 3), the Eckert number Ec, the Brinkman number Br, the Sisko fluid parameter β*, and the variable viscosity parameter μ. Here, we consider the space dependent variable viscosity[33],
, the Reynolds number Re, the Prandtl number Pr, the elasticity parameters Ei(i=1, 2, 3), the Eckert number Ec, the Brinkman number Br, the Sisko fluid parameter β*, and the variable viscosity parameter μ. Here, we consider the space dependent variable viscosity[33],
The pressure is found independent of the radial coordinate. Thus, combining Eqs. (12) and (13) for the stream function, one has

|
(19) |

|
(20) |

|
(21) |

|
(22) |

|
(23) |

|
(24) |
where the subscripts represent partial derivatives.
3 Solution methodology The obtained mathematical expressions are complex due to the non-linear fluid parameter β*. Such complexity in terms of solutions can be controlled with the suitable approximation technique. Therefore, in this section, the perturbation and numerical shooting of the problem can be conducted. Moreover, the graphical solutions obtained through both the techniques in terms of the velocity and temperature are compared and discussed. Note that the power index is kept at the constant value n=3 throughout the analysis.
3.1 Perturbation method Here, we intend to obtain the perturbed solution about the small fluid parameter β* in the following form:
3.1.1 Zeroth-order system

|
(25) |

|
(26) |

|
(27) |

|
(28) |

|
(29) |
3.1.2 First-order system

|
(30) |

|
(31) |

|
(32) |

|
(33) |

|
(34) |
The obtained solutions followed by the above scheme are lengthy. Therefore, the solution expressions are avoided here. However, they have been used to plot the graphical results corresponding to the perturbation technique.
3.2 Numerical method This subsection presents the graphical description of the above problem numerically. Thus, built-in routine of MATHEMATICA NDSolve based on the shooting method has been exploited here. Here, the whole system of Eqs. (19)-(24) is directly substituted for graphical sketches of the axial velocity u and the temperature θ, respectively.
4 Results and discussion Here, an interpretation to figures is assigned. More specifically, comparison of results obtained with the perturbation and numerical approaches has been highlighted for u and θ with variation of the Sisko fluid parameter β*, wall parameters Ei(i=1, 2, 3), the curvature parameter k, the Brinkman number Br, and the viscosity parameter α. The streamline pattern is also captured for involved parameters of interest.
4.1 Velocity distribution The outcome of the axial velocity u towards an increase in the variable viscosity parameter α, the elasticity parameter E1, the mass characterizing parameter E2, the damping parameter E3, the fluid parameter β*, and the curvature parameter k has been developed and analyzed in this subsection. A decrease in u for the larger α is noticed for both numerical and perturbation techniques. In reference to small blood vessels, the fluid viscosity varies with the thickness of vessel. For the larger viscosity, the dense fluid particles move with lower velocities (see Fig. 1). With an enhancement in E1, the fluid viscosity weakens because particles move with greater velocities (see Fig. 2). As the mass per unit area increases, the particles of fluid move freely to produce the velocity uplift. Moreover, the range of the velocity increase corresponding to the perturbed solution is small compared with the numerical solution (see Fig. 3). Since damping acts to resist the flow speed due to energy loss, a decreasing response of E3 is captured in Fig. 4 for both perturbation and numerical approaches. Clinically, when walls of blood are elastic or the mass per unit area increases (as in blood capillaries), exchange of water, oxygen, and other nutrients becomes easy. However, the damping tends to respond oppositely. Such results agree with the observations through perturbation and various numerical schemes (see Refs.[21]-[24]). The behavior of u towards the increase in β* appears decreasing since larger β* dominates the shear thickening effect which opposes the fluid motion (see Fig. 5). Impacts of curvature on the velocity distribution are decreasing as a whole. However, the dual response of k is seen when the perturbation method is accounted, that is, u rises when 0 < r < 0.5 (see Fig. 6).
4.2 Temperature distribution This subsection presents the physical description of the temperature θ towards variation of embedding parameters in both cases (perturbation and numerical solutions) through Figs. 7-10. The variable viscosity tends to reduce the temperature profile with its growing values (see Fig. 7). The purpose of viscous dissipation is to catalyze the heat transfer by the fluid, hence the temperature rises with Br (see Fig. 8). Also, results are more signified when the problem is executed numerically. Increasing values of β* show a reduction in the temperature of fluid (see Fig. 9). The impression of curvature on the temperature is decreasing in both perturbation and numerical cases (see Fig. 10).
4.3 Streamline pattern When fluids are flowing peristaltically in bounded domains (channel, tube, and duct), the flow structures experience various patterns such as backward flows, trapping or streamlines. The phenomenon is beneficial in providing the information whether the fluid is transported directly from entrance to exit, or if a portion of it is trapped within the channel, and also where it is trapped in the provided range. When the fluid patterns are trapped near channel boundaries, they form streamlines. The variation of the streamline pattern for the considered geometry has been developed in this subsection. It is seen from Figs. 11(a) and 11(b) that the size of trapped bolus reduces in the upper half space whereas it expands near the lower half space when k increases. Growing values of α enhance the number of streamlines while the trapped bolus shrinks upon an increase in α (see Figs. 12(a) and 12(b)). Larger values of β* reduce the number of streamlines. However, the size of bolus remains nearly unchanged (see Figs. 13(a) and 13(b)).
5 Conclusions Heat transfer in peristaltic transport of Sisko fluids in a curved channel is addressed. Main points are listed below.
(ⅰ) The outcomes of numerical and perturbation schemes are qualitatively alike.
(ⅱ) Decline in the flow velocity and temperature is noticed as the viscosity parameter increases.
(ⅲ) Elasticity of wall activates the fluid velocity where damping tends to resist the flow speed.
(ⅳ) The fluid velocity and temperature are reduced with the curvature.
(ⅴ) The response of Sisko fluid parameter towards the velocity and temperature is decreasing.
(ⅵ) Viscous dissipation increases the fluid temperature.
(ⅶ) Trapped bolus expands with curvature whereas the minute response is noticed for larger α and β*.







































































 2018, Vol. 39
2018, Vol. 39


