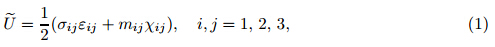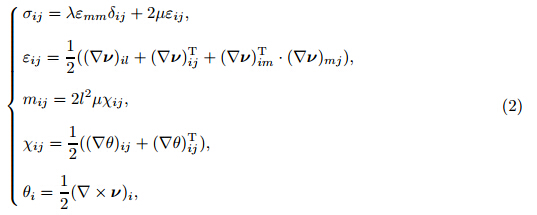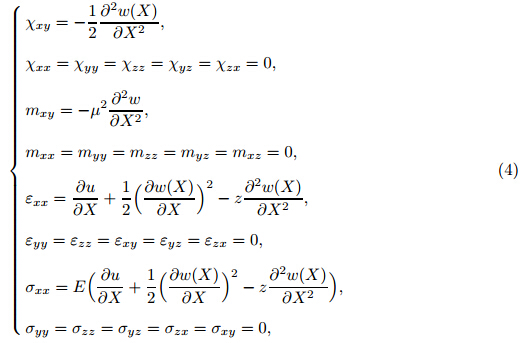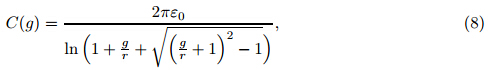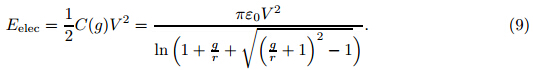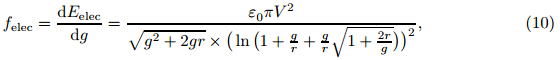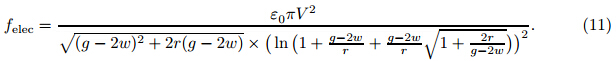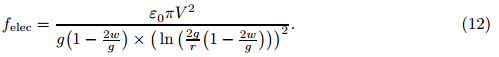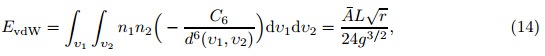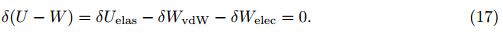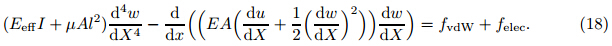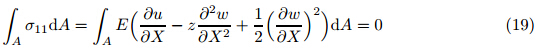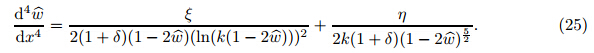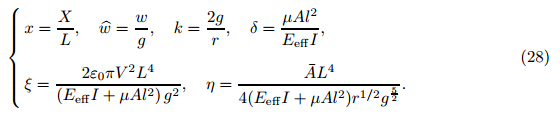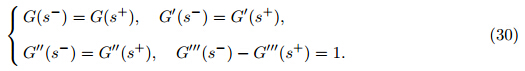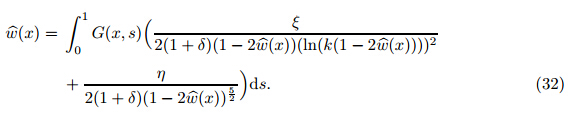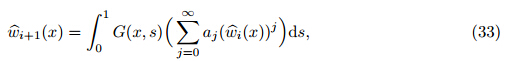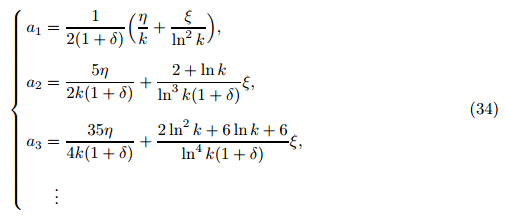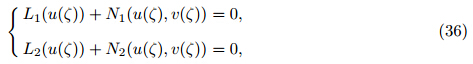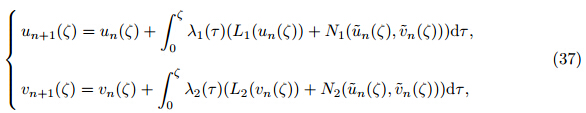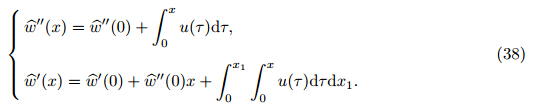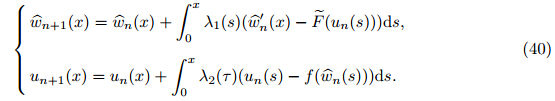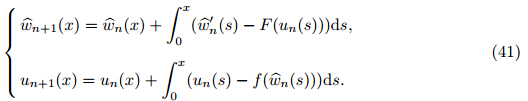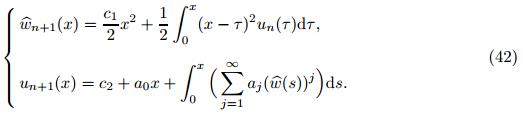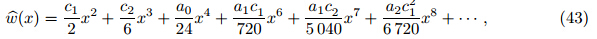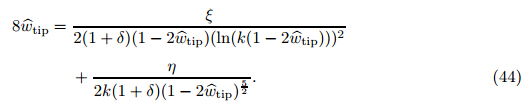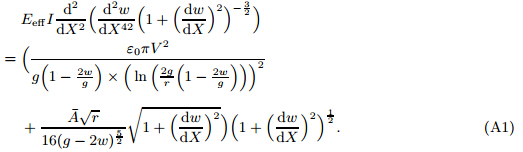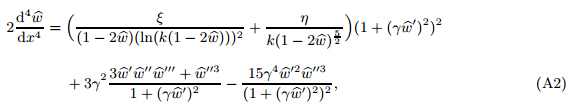Shanghai University
Article Information
- A. FARROKHABADI, A. KOOCHI, A. KAZEMI, M. ABADYAN. 2014.
- Effects of size-dependent elasticity on stability of nanotweezers
- Appl. Math. Mech. -Engl. Ed., 35(12): 1573-1590
- http://dx.doi.org/10.1007/s10483-014-1880-6
Article History
- Received 2013-08-07;
- in final form 2014-05-01
2. Mechanical Engineering Group, Shahrekord Branch, Islamic Azad University, Shahrekord 88137-33395, Iran;
3. Department of Physics, University of Bath, Bath BA2-7AY, United Kingdom
In recent decades,nanotechnology revolution enabled engineers to develop the ultra-small devices which are extremely beneficial in many branches of science,including nanoelectronics, nanobiology,material science and chemistry,nanophotonics,and nanomechanics. These ultrasmall devices have been used to discover the submicron world and to fabricate tiny ultra-efficient instruments. Nanotweezers are smart miniature device utilized to manipulate nanoelements,to investigate nanoparticle interaction,and to measure the characteristics of nanomaterials [1] . The device is constructed from two clamped conductive elements (arms). If a direct current (DC) potential difference is applied among the conductive elements,they will come closer to each other as a result of Coulomb attraction. When the applied potential exceeds the pull-in limit,the arms will lose the stability and adhere each other. It restricts the tweezing range of the tweezers. With this regard,determining the pull-in characteristics is crucial for fabricating trustworthy nanotweezers. Kim and Lieber [2] experimentally evaluated the pull-in voltage of carbon nanotube-based tweezers. Several frameworks can be employed for modeling the electromechanical behavior of nanostructures. Molecular computation might be employed to simulate the physical response of nanoscale objects [3] . However,molecular simulation is time-consuming and cannot be easily used for modeling the nanodevices constructed from many molecules. Therefore,continuum nanoscale models are usually considered as reliable alternatives [4, 5, 6, 7] .
At nanoscale,where the gap between interacting bodies decreases to few nanometers,the intermolecular attraction,i.e.,van der Waals force,predominates. Evaluation of the impact of intermolecular attractions on the stability of ultra-small systems is very crucial for the fabrication of nanotweezers and nanodevices [8, 9, 10, 11, 12] . Wang et al. [13] investigated the influence of intermolecular forces on the stability of freestanding nanotube-based nanotweezers by a continuum mechanics model,where nanotubes with different geometrical characteristics were considered and the Galerkin technique was used as the solution method.
An important phenomenon that becomes significant at ultra-small scales is the size-dependent response of structures and materials. Some experiments reveal that if the dimensions of metallic elements become comparable with or less than the metal length-scale parameter values, their physical characteristics will become highly size dependent [14, 15, 16] . Lam et al. [15] reported that the decrease in the thickness of polymeric rods from 115 µm to 20 µm results in about 240% increase in the flexural rigidity of the microbeams. McF arland and Colton [16] experimentally investigated the flexural behavior of polypropylene micro-cantilevers. Their measurements showed that the rigidity of the elements was 400% greater than that determined by classic theories. The size-dependent characteristics of materials and elements at ultra-small scales might not be interpreted by classic continuum theories. To conquer this limitation,different sizedependent elasticities,e.g.,nonlocal [17, 18] ,couple-stress [19, 20] ,and modified couple-stress [21] , are introduced. The modified couple-stress elasticity (MCSE) [21] introduces only one intrinsic length scale constant for modeling the size-dependency of materials in small scales. It has been employed to investigate beam-type elements [22, 23, 24] and model the stability of nanoelectromechanical systems (NEMSs) [25, 26, 27] .
Herein,MCSE is applied to demonstrate the size effect on the stability of nanotweezers. The Coulomb and intermolecular forces are considered in the model. Four solution techniques,i.e., the modified variational iteration method (MVIM),the monotonic iteration method (MIM), the lumped parameter model (LPM),and the MAPLE numerical solver,are employed. The results are comparison with the literatures. 2 Theoretical model
A typical nanowire based nanotweezer is employed,which is constructed from two clamped conductive wires (arms) with the length L and the radius r (see Fig. 1). The distance between the cantilever nanowires is g.
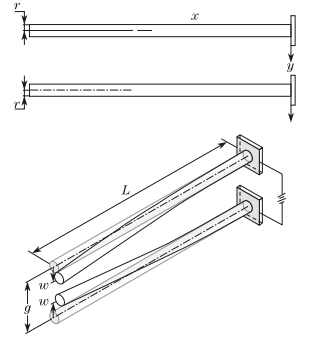 |
| Fig. 1 Representation of nanotweezers and geometrical parameters |
Considering the MCSE [21] ,the elastic energy density of a continuum U can be written as
where σ ij and ε ij are Cauchy’s stress components and von-Karman’s strain components,respectively. mij and χij are the deviatoric couple stress components and the symmetric curvature components,respectively. These components are determined by where ν and θ are the displacement vector and the rotation vector,respectively. µ and λ are the shear modulus and the Lame constant,respectively. l is the length-scale constant that is an intrinsic material characteristic. As the characteristic length of the deformation field becomes significantly greater than the inherent material length-scale characteristic,the influence of the gradients of strains become insignificant,because the strain components are substantially large in comparison with the corresponding scaled gradient components [28] . In this case,the results obtained by the MCSE are the same as those obtained by classic continuum theory. The value of the length scale parameter of a material is reported in a wide range from several angstroms [29] to several micrometers [15] based on the material type and the determination approach. The elastic modulus of zinc oxide nanowires increases significantly with the decrease in the wire radius below 60 nm [30] . The length scale parameters for polypyrrole [31] and polycaprolactone [32] are determined as 43 nm and 69 nm,respectively. Molecular dynamic simulations can be utilized to compute the length-scale constants of materials [29] . With this approach,very small values are predicted for non-local length scale parameters [29] ,e.g.,of the order of few angstroms (< 1 nm) for copper,aluminum,etc. and few nanometers for polythene (< 10 nm),which are much smaller than the values of the length scale parameters predicted by previous researchers [29, 31, 32] .For each arm,the displacement is expressed as [33]
Considering small deformation and substituting Eq. (3) in Eq. (2) yield where E is Young’s modulus.Substituting Eq. (4) in Eq. (1) yields the strain energy as follows:
In the above relation, X,A,and I are the distantance from the clamped end,the crosssection area of the nanowires,and the crosssectional moment of inertia,respectively.Furthermore,considering the intermolecular and electrostatic Coulomb attractions yields the work of the external forces as follows:
2.2 Electrostatic Coulomb attractionThe Coulomb attraction is determined by the cylindrical capacitance model [34] . The nanowires are assumed to be perfectly conductive. The capacitance per unit length for parallel cylindersis [35]
where ε 0 is the vacuum permittivity. The Coulomb energy is Now,the Coulomb attraction per unit length,f elec,can be extracted from Eq. (9) as follows: where V is the voltage difference,and w1 and w2 are the deflections of nanowires. Imposing the DC voltage difference causes the nanowires to displace towards each another. Therefore,the gap will decrease from g to g − w1 − w2. If both arms of the nanotweezers are similar,they will have the same displacement (w1 = w2 = w). Therefore,by replacing g withg − 2w in Eq. (10), we have We assume that the radius of the nanowire (r) is negligible in comparison with the initial gap among the nanowires (g),i.e.,r << g. Then,the Coulomb attraction can be approximated as 2.3 Van der Waals forceIn this work,the well-established Lennard-Jones atomic potential is used to compute the intermolecular attraction between bodies [36] . According to this approach,the potential for atoms i and j can be expressed as
where d ij is the distance between the two atoms. C6 and C12 are the attractive and repulsive parameters,respectively. They are constants. For distances large enough,e.g.,d ij > 0.34 nm, the repulsive component can be omitted [17] . Then,the intermolecular energy can be determined by integration of the atomic potential over the volume of interacting bodies [37, 38, 39] . Therefore, the intermolecular energy EvdW can be expressed as where υ 1 and υ 2 represent the volumes of the interacting bodies (nanowires),and n1 and n2 are the atomic densities of the bodies. d(υ 1,υ 1 ) defines the distance between any two elements on the interacting bodies.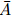 ,which is in the range from 0.4 × 10
−19
J to 4 × 10
−19
J,is the Hamakerconstant
[12]
,and r is the external radius of the nanowires. The intermolecular attraction per
unit length extracted from Eq. (14) is
By assuming the identical geometry of the arms,the displacements of w1
and w2
will be the
same,i.e.,
,which is in the range from 0.4 × 10
−19
J to 4 × 10
−19
J,is the Hamakerconstant
[12]
,and r is the external radius of the nanowires. The intermolecular attraction per
unit length extracted from Eq. (14) is
By assuming the identical geometry of the arms,the displacements of w1
and w2
will be the
same,i.e.,
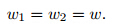
Based on the equilibrium condition,the total energy of the system can be minimized as follows:
Finally,the equilibrium state of the nanowire arms can be obtained by Eq. (17) as the following boundary value problem: The static equilibrium of cantilever beam implies that the normal resultant along the beam is zero. Therefore, or Substituting Eq. (20) in Eq. (18) yields the nonlinear ordinary differential equation (ODE) for nanowire based tweezers as follows: The geometrical boundary condition at the fixed end is The natural boundary condition at the free end isWithout mid-plane stretching,substituting the Coulomb and intermolecular attractions in Eq. (21) yields
Then,the non-dimensional ODE of the system can be obtained as follows: The geometrical boundary condition at the fixed end is The natural boundary condition at the free end is where It is noted that by considering the simplification in Section 2.3,when the size effect and the external applied voltage are neglected,the obtained governing equation is similar to that in Ref. [13]. Moreover,for large deflection cases,the effect of curvature may be considered in the model to obtain more precise results (see Appendix A). 3 Solving equationsFour methods,i.e.,a lumped model,the MIM,the MVIM,and the MAPLE numerical solver, are conducted. 3.1 MIM
The response of the nanotweezers to a arbitrary distributed force can be determined by understanding the arbitrary force and the solution for a concentrated force. Therefore,one can find the solution for the concentrated load by the Dirac delta function (δD) and solving the following equation:
Then,Green’s function must satisfy Eqs. (26) and (27) and the following conditions [25] : Green’s function of our problem is defined as follows [40] : According to the MIM,the solution of Eq. (25) can be determined as follows (see Ref. [25] for details): With the Taylor expansion and iteration operation,Eq. (32) can be recast as follows [25] : where a jare the Taylor expansion coefficients of the force term integrand in Eq. (32),i.e.,
As an initial guess,the deformed shape of the arms is approximated by  (x) =
(x) = 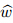 tip
x
2
. This
proposed approximated shape function satisfies Eq. (26)
[41]
. In this work,three iterations are
performed to determine the nanowire displacement. The instability is determined via the slope
of the b
tip
x
2
. This
proposed approximated shape function satisfies Eq. (26)
[41]
. In this work,three iterations are
performed to determine the nanowire displacement. The instability is determined via the slope
of the b 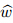 -ξ graphs.
3.2 MVIM
-ξ graphs.
3.2 MVIM
To solve the equation by the MVIM,Eq. (25) is transformed by T aylor expansion as follows:
Based on the MVIM,the following nonlinear system is considered [40, 41, 42, 43] : where L1(u(ζ )) and L2(u(ζ )) are linear operators,and N1(u(ζ ),v (ζ )) and N2(u(ζ ),v (ζ )) are nonlinear operators. Now,the corrective functions for the system of Eq. (36) are established as follows: where λ1(τ ) and λ1(τ ) are Lagrange multipliers. u n and v n are the nth approximations satisfying the restrictions as follows: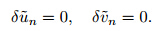
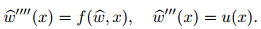
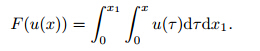
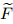 (u
n
(s)) and
(u
n
(s)) and 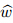 n
(s) satisfy
n
(s) satisfy
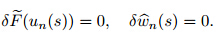
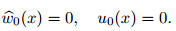
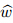 0
′′
(0) = c
1
and considering Eq. (26) yield
Substituting n = 2 in Eq. (42) yields
where c1
and c
2 can be obtained by Eq. (27).
3.3 Numerical solution
0
′′
(0) = c
1
and considering Eq. (26) yield
Substituting n = 2 in Eq. (42) yields
where c1
and c
2 can be obtained by Eq. (27).
3.3 Numerical solutionBesides the analytical results,the governing equation of the nanotweezers can be numerically solved. The governing ODE of Eq. (25) is solved by the MAPLE solver. The pull-in parameters of the tweezers are obtained via the slope of the w-ξ graphs. 3.4 LPM To establish a simple lumped model,the mechanical behavior of the tweezers can be expressed by a Hookean spring with a spring constant of 8Eeff I/L [25] . The approach is illustrated in Fig. 2. The LPM presumes a uniform distribution of intermolecular and Coulomb attractions along the wires. Therefore,the LPM constitutive relation for the nanowire can be derived as follows:
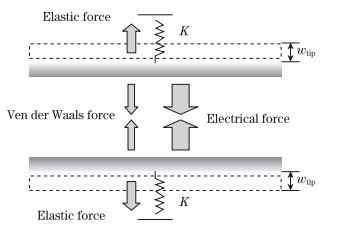 |
| Fig. 2 Schematic configuration of LPM |
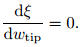
For the LPM,the instability parameters are determined by Eq. (44) by setting
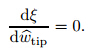
Figure 3 shows the variation of the displacement of the nanowires when the applied DC
voltage varies from zero to an instability voltage. As shown in Fig. 3,elevating the applied voltage results in the increase in the wires deflection. When the DC voltage exceeds the maximum
stable value,i.e.,the pull-in voltage ξ
PI
,the arms will exceed their maximum stable deflection,
i.e.,the pull-in deflection 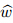 PI
,and the arms will suddenly adhere each another. The operating
range of the nanotweezers is restricted by the pull-in phenomenon.
PI
,and the arms will suddenly adhere each another. The operating
range of the nanotweezers is restricted by the pull-in phenomenon.
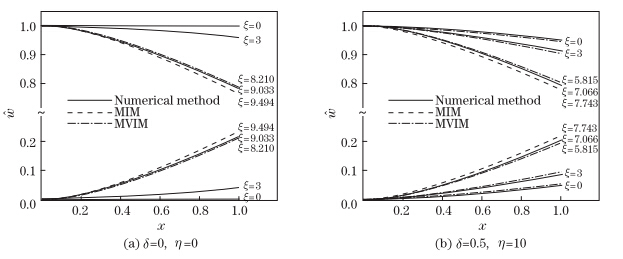 |
| Fig. 3 Deflection of nanotweezer arms with k = 10 for ξ ∈ [0,π] |
The nanoscale effects in Fig. 3(a) are neglected,while both the intermolecular attraction
and the size effect are taken to account in Fig. 3(b). From Fig. 3(b),we can see that the
nanotweezers have an initial deflection even in the absence of Coulomb charge. This is due to
the presence of the intermolecular attraction. Furthermore,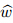 PI
and ξ
PI
of the nanotweezers are
decreased (see Fig. 3(b)). Since the intermolecular force and size effect induce the hardening
effect,the instability characteristics of the nanotweezers decrease. In the following,we first
evaluate the validity of the proposed approach by comparison with the experiments reported in
Ref. [47]. Afterwards,the influence of the nanoscale phenomena (intermolecular attraction and
size effect) on the electromechanical stability of the tweezers is discussed.
4.1 Comparison with experiments
PI
and ξ
PI
of the nanotweezers are
decreased (see Fig. 3(b)). Since the intermolecular force and size effect induce the hardening
effect,the instability characteristics of the nanotweezers decrease. In the following,we first
evaluate the validity of the proposed approach by comparison with the experiments reported in
Ref. [47]. Afterwards,the influence of the nanoscale phenomena (intermolecular attraction and
size effect) on the electromechanical stability of the tweezers is discussed.
4.1 Comparison with experiments
In Ref. [47],the pull-in voltage of the carbon wire nanotweezers with 19.6 µm length,6.9 µm initial gap,and 300 nm diameter were measured. The snap down voltage of 102 V were reported for the tweezers [47] . The results obtained by Ref. [47] and the classical and couple stress theory are illustrated in Fig. 4.
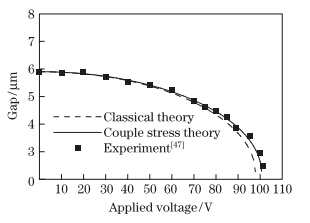 |
| Fig. 4 Stability behaviors of tweezers obtained by different theories |
As seen in Fig. 4,the experimental measurements are slightly different from the numerical values obtained by the classic continuum model. However,with the presented size-dependent model and considering the material length scale parameter l = r/10,one can find excellent consistency between them. It confirms that the proposed approach is reliable for investigating device stability. 4.2 Effect of intermolecular attraction
If the gap between the arms of the nanotweezers is at nanoscale,the simultaneous presence
of electrostatic and intermolecular interactions will be included in the theoretical model. The
effects of intermolecular attraction η on the dimensionless instability voltage ξ
PI
and the deflection  PI
of the nanotweezers are illustrated in Fig. 5 and Fig. 6,respectively. As seen in Fig. 5 and Fig. 6,when the intermolecular attraction increases,both the instability parameters decrease. The
intersections of the lines with the η-axis correspond to a critical value of intermolecular force
η
C. If the nanowires come close enough to each other,adhesion will happen even in the absence
of Coulomb attraction. The maximum wire length Lmax,required to intercept the stiction of
the freestanding wires (in the absence of Coulomb attraction),is named as the detachment
length
[48]
. Similarly,for a specific length of the nanowires,there is a minimum gap,g
min,
which intercepts the adhesion of the nanowires. Lmax and g
min are important characteristics in
designing reliable nanotweezers.
PI
of the nanotweezers are illustrated in Fig. 5 and Fig. 6,respectively. As seen in Fig. 5 and Fig. 6,when the intermolecular attraction increases,both the instability parameters decrease. The
intersections of the lines with the η-axis correspond to a critical value of intermolecular force
η
C. If the nanowires come close enough to each other,adhesion will happen even in the absence
of Coulomb attraction. The maximum wire length Lmax,required to intercept the stiction of
the freestanding wires (in the absence of Coulomb attraction),is named as the detachment
length
[48]
. Similarly,for a specific length of the nanowires,there is a minimum gap,g
min,
which intercepts the adhesion of the nanowires. Lmax and g
min are important characteristics in
designing reliable nanotweezers.
 |
| Fig. 5 Impact of intermolecular force on ξPI of nanotweezers with k = 10 and δ = 0 |
 |
Fig. 6 Impact of intermolecular attraction
on  PI of nanotweezers with k = 10
and δ = 0 PI of nanotweezers with k = 10
and δ = 0 |
Neglecting the sub-micron intermolecular attractions is a common practice in micro-tweezers literature. However,the size effect may substantially affect the electromechanical response of the micro-tweezers even in micron-scale where the impact of intermolecular interactions is negligible.
Figure 7 implies the impact of the size effect on the instability voltage of micro-tweezers without the incorporating intermolecular interaction. As seen in Fig. 7,there is a linear relation between ξ PI and δ,i.e.,the increase in δ results in the increase in ξ PI . Figure 8 depicts that the maximum stable deflection of the microtweezers is not affected by the size effect phenomenon.
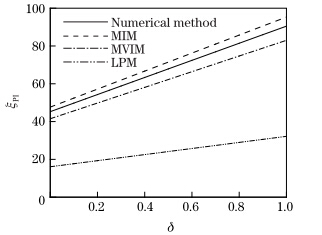 |
| Fig. 7 Impact of intermolecular force on ξPI of mi |
At nanoscale,both the intermolecular interactions and the size dependency phenomena must be included in the simulation of the nanotweezers instability. Figure 9 depicts the impact of size phenomena on the instability voltage of the nanotweezers with η = 10 and k = 10. From Fig. 9,one can conclude that the increase in the size effect results in elevating the maximum stable voltage of the tweezers. Figure 10 demonstrates the variation of b wPI versus δ in the presence of nanoscale attraction.
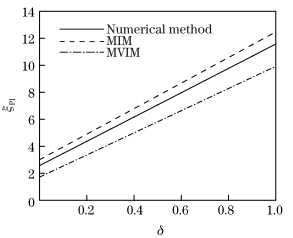 |
| Fig. 9 Impact of size phenomenon on ξPI of nanotweezers with η = 10 and k = 10 |
As seen in Fig. 10,the maximum stable deflection of the nanotweezers gradually increases by
increasing the size effect. It is noticed that the observed trend differs from the flat trend
in Fig. 8 where b wPI
is not altered in the absence of intermolecular force. In addition,the
comparison between Figs. 9 and 10 implies that ξ
PI
is much more sensitive to the size dependency
phenomenon in comparison with  PI
.
PI
.
 |
Fig. 10 Impact of size phenomenon on 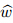 PI
of nanotweezers with η = 10 and
k = 10 PI
of nanotweezers with η = 10 and
k = 10 |
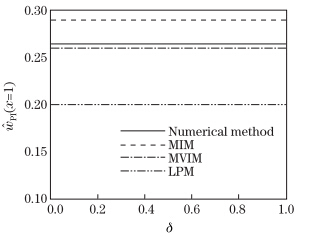 |
Fig. 8 Impact of size phenomenon on 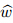 PI
of microtweezers with k = 100 and
η = 0 PI
of microtweezers with k = 100 and
η = 0 |
The relations between the applied voltage and the centerline tip deflection are presented
in Fig. 11 for various k. As shown in Fig. 11,when the DC voltage elevates,the tip deflection
increases until the wires lose their stability. The intersections of the lines with the horizontal axis
correspond to the initial tip deflection of nanotweezers induced by the intermolecular attraction
(see Fig. 11). Moreover,Fig. 11 reveals that the effect of the intermolecular interaction on the
tweezing range of tweezers with k 400 is negligible. This means that if the gap is 100 times
larger than the arm diameter,the intermolecular force cannot effectively change the initial
deflection and the maximum stable deflection of the system.
400 is negligible. This means that if the gap is 100 times
larger than the arm diameter,the intermolecular force cannot effectively change the initial
deflection and the maximum stable deflection of the system.
The effect of k on the instability characteristics of the nanotweezers is demonstrated in Fig. 12. As shown in Fig. 12,enhancing k will increase ξ PI .
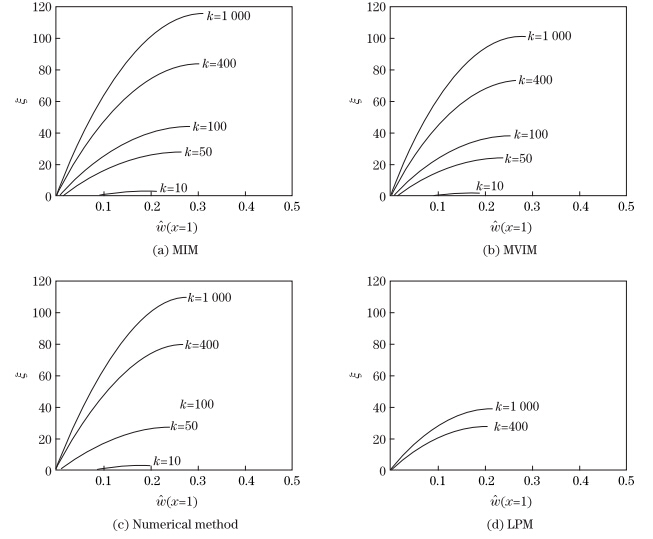 |
| Fig. 11 Relations between wire tip deflection and dimensionless voltage for various k with η = 10 and δ = 0 |
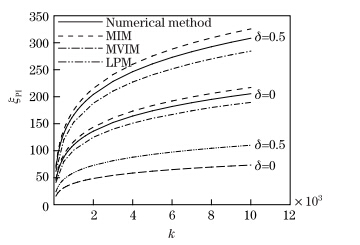 |
| Fig. 12 Impact of k on instability voltage of microtweezers with η = 0 |
The obtained results reveal that the MIM solution overestimates the instability parameters of the nanotweezers,the MVIM solution underestimates the instability characteristics of the nanotweezers,and the MIM solution provides higher accuracy in approximating the instability voltage. Therfore,the MVIM is more precise for determining the instability deflection of the system.
Moreover,it can be concluded that the proposed LPM is not precise for determining the stability characteristics of the system,especially the instability voltage. However,it is suitable for investigating the physicomechanical response of a system without undue computational complexities. 5 Conclusions
The MCSE is employed to investigate the impact of the size effect phenomenon and the intermolecular attraction on the electromechanical stability of nanotweezers. The obtained results imply that:
(i) The presence of intermolecular force reduces the maximum stable voltage of the system. It induces an initial deflection in the nanotweezers,and reduces the maximum stable deflection of the nanotweezers.
(ii) In the absence of intermolecular force,the increase in the size effect enhances the instability voltage of microtweezers. Moreover,the size phenomenon does not alter the instability deflection of the microtweezers.
(iii) By considering intermolecular interactions,the increase in the size parameter enhances both the instability parameters of the nanotweezers. The instability voltage is much more sensitive to the size dependency phenomenon rather than the instability deflection.
(iv) The increase in k results in the increase in the pull-in parameters. If the gap becomes 100 times larger than the arm diameter,i.e.,k > 400,the van der Waals force cannot effectively change the deflection characteristics and tweezing range of the system.
(v) The MIM solution overestimates the instability parameters of nanotweezers,while the MVIM solution underestimates the instability parameters of nanotweezers. The MIM solution is more accurate in computing the instability voltage,but the MVIM is appropriate for calculating the nanotweezers deflection. The LPM does not offer high-precision results,but it demonstrates the nature of the instability phenomenon.
Appendix A Large displacement theoryIf nanotweezers expose large displacements,the effect of curvature is incorporated in the theoretical model. In this case (for the classic continuum theory),the governing equation is modified to [49] :
After some elaborations,from Eq. (28),the dimensionless constitutive equation can be obtained as follows:
where When γ approaches zero,Eq. (A2) is simplified to Eq. (25).To evaluate the present model,the instability parameters of typical nanotweezers for different k are evaluated. The numerical results presented inTable 1 and Table 2 imply the effects of small and large deflection on the instability. It is shown that the effect of large deflection is insignificant,and Eq. (25) is precise enough for determining the response of nanotweezers for low values of the gap to length ratio. This is common in the design and fabrication of nanotweezers.
 |
 |
| [1] | Farrokhabadi, A., Rach, R., and Abadyan, M. Modeling the static response and pull-in instability of CNT nanotweezers under the Coulomb and van der Waals attractions. Physica E, 53, 137-145 (2013) |
| [2] | Kim, P. and Lieber, C. M. Nanotube nanotweezers. Science, 286, 2148-2150 (1999) |
| [3] | Sasaki, N., Toyoda, A., Sayito, H., Itamura, N., Ohyama, M., and Miura, K. Theoretical simula-tion of atomic-scale peeling of single-walled carbon nanotube from graphite surface. e-Journal of Surface Science and Nanotechnology, 4, 133-137 (2006) |
| [4] | Ke, C. H., Pugno, N., Peng, B., and Espinosa, H. D. Experiments and modeling of carbon nanotube NEMS device. Journal of the Mechanics and Physics of Solids, 53, 1314-1333 (2005) |
| [5] | Jiang, L., Tan, H., Wu, J., Huang, Y., and Hwang, K. C. Continuum modeling of interfaces in polymer matrix composites reinforced by carbon nanotubes. Nano, 2, 139-148 (2007) |
| [6] | Koochi, A., Kazemi, A. S., Noghrehabadi, A., Yekrangi, A., and Abadyan, M. New approach to model the buckling and stable length of multi walled carbon nanotube probes near graphite sheets. Materials and Design, 32, 2949-2955 (2011) |
| [7] | Farrokhabadi, A., Koochi, A., and Abadyan, M. Modeling the instability of CNT tweezers using a continuum model. Microsystem Technologies, 20, 291-302 (2014) |
| [8] | Noghrehabadi, A., Ghalambaz, M., Beni, Y. T., Abadyan, M., Abadi, M. N., and Abadi, M. N. A new solution on the buckling and stable length of multi wall carbon nanotube probes near graphite sheets. Procedia Engineering, 10, 3725-3733 (2011) |
| [9] | Noghrehabadi, A., Ghalambaz, M., and Ghanbarzadeh, A. Buckling of multi wall carbon nan-otube cantilevers in the vicinity of graphite sheets using monotone positive method. Journal of Computational and Applied Research in Mechanical Engineering, 1, 89-97 (2012) |
| [10] | Lin, W. H. and Zhao, Y. P. Casimir effect on the pull-in parameters of nanometer switches. Microsystem Technologies, 11, 80-85 (2005) |
| [11] | Guo, J. G. and Zhao, Y. P. Influence of van der Waals and Casimir forces on electrostatic torsional actuators. Journal of Microelectromechanical Systems, 13, 1027-1035 (2004) |
| [12] | Guo, J. G. and Zhao, Y. P. Dynamic stability of electrostatic torsional actuators with van der Waals effect. International Journal of Solids and Structures, 43, 675-685 (2006) |
| [13] | Wang, G. W., Zhang, Y., Zhao, Y. P., and Yang, G. T. Pull-in instability study of carbon nanotubes tweezers under the influence of van der Waals forces. Journal of Micromechanics and Microengineering, 14, 1119-1125 (2004) |
| [14] | Fleck, N. A., Muller, G. M., Ashby, M. F., and Hutchinson, J. W. Strain gradient plasticity: theory and experiment. Acta Metallurgica et Materialia, 42, 475-487 (1994) |
| [15] | Lam, D. C. C., Yang, F., Chong, A. C. M., Wang, J., and Tong, P. Experiments and theory in strain gradient elasticity. Journal of the Mechanics and Physics of Solids, 51, 1477-1503 (2003) |
| [16] | McFarland, A. W. and Colton, J. S. Thermoplastic polymer microcantilever sensors fabricated via micromolding. Journal of Micromechanics and Microengineering, 15, 1060-1067 (2005) |
| [17] | Aydogdu, M. A general nonlocal beam theory: its application to nanobeam bending, buckling and vibration. Physica E, 41, 1651-1655 (2009) |
| [18] | Yang, J., Ke, L. L., and Kitipornchai, S. Nonlinear free vibration of single-walled carbon nanotubes using nonlocal Timoshenko beam theory. Physica E, 42, 1727-1735 (2010) |
| [19] | Ejike, U. B. The plane circular crack problem in the linearized couple-stress theory. International Journal of Engineering Science, 7, 947-961 (1969) |
| [20] | Kishida, M. and Sasaki, K. Torsion of a circular bar with annular groove in couple-stress theory. International Journal of Engineering Science, 28, 773-781 (1990) |
| [21] | Yang, F., Chong, A. C. M., Lam, D. C. C., and Tong, P. Couple stress based strain gradient theory for elasticity. International Journal of Solids and Structures, 39, 2731-2743 (2002) |
| [22] | Park, S. K. and Gao, X. L. Bernoulli-Euler beam model based on a modified couple stress theory. Journal of Micromechanics and Microengineering, 16, 2355-2359 (2006) |
| [23] | Tadi-Beni, Y., Koochi, A., Kazemi, A. S., and Abadyan, M. Theoretical study of the effect of Casimir force, elastic boundary conditions and size dependency on the pull-in instability of beam-type NEMS. Physica E, 43, 979-988 (2011) |
| [24] | Ma, H. M., Gao, X. L., and Reddy, J. N. A microstructure-dependent Timoshenko beam model based on a modified couple stress theory. Journal of the Mechanics and Physics of Solids, 56, 3379-3391 (2008) |
| [25] | Abdi, J., Koochi, A., Kazemi, A. S., and Abadyan, M. Modeling the effects of size dependence and dispersion forces on the pull-in instability of electrostatic cantilever NEMS using modified couple stress theory. Smart Materials and Structures, 20, 055011 (2011) |
| [26] | Baghani, M. Analytical study on size-dependent static pull-in voltage of microcantilevers using the modified couple stress theory. International Journal of Engineering Science, 54, 99-105 (2012) |
| [27] | Zhang, J. and Fu, Y.Pull-in analysis of electrically actuated viscoelastic microbeams based on a modified couple stress theory, Meccanica, 47, 1649-1658 (2012) |
| [28] | Wang, W., Huang, Y., Hsia, K. J., Hu, K. X., and Chandra, A. A study of microbend test by strain gradient plasticity. International Journal of Plasticity, 19, 365-382 (2003) |
| [29] | Maranganti, R. and Sharma, P. A novel atomistic approach to determine strain-gradient elasticity constants: tabulation and comparison for various metals, semiconductors, silica, polymers and the (Ir) relevance for nanotechnologies. Journal of the Mechanics and Physics of Solids, 55, 1823-1852 (2007) |
| [30] | Chen, C. Q., Shi, Y., Zhang, Y. S., Zhu, J., and Yan, Y. J. Size dependence of Young's modulus in ZnO nanowires. Physical Review Letters, 96, 075505 (2006) |
| [31] | Cuenot, S., Demoustier-Champagne, S., and Nysten, B. Elastic modulus of polypyrrolenanotubes. Physical Review Letters, 85, 1690-1693 (2000) |
| [32] | Liang, S., Han, R. P. S., Wang, J., and Lim, C. T. Modeling the size-dependent elastic properties of polymeric nanofibers. Nanotechnology, 19, 455706 (2008) |
| [33] | Timoshenko, S. Theory of Plates and Shells, McGraw-Hill, New York (1987) |
| [34] | Jackson, J. D. Classical Electrodynamics, Wiley, New York (1998) |
| [35] | Hayt, W. H. Engineering Electromagnetics, McGraw-Hill, New York (1981) |
| [36] | Lennard-Jones, J. E. Perturbation problems in quantum mechanics. Proceedings of the Royal Society of London. Series A, 129, 598-615 (1930) |
| [37] | Girifalco, L. A., Hodak, M., and Lee, R. S. Carbon nanotubes, buckyballs, ropes, and a universal graphitic potential. Physical Review B, 62, 13104-13110 (2000) |
| [38] | Ke, C. H. and Espinosa, H. D. The Handbook of Theoretical and Computational Nanotechnology, American Scientific Publishers, Valencia (2006) |
| [39] | Israelachvili, J. N. Intermolecular and Surface Forces with Applications to Colloidal and Biological Systems, Academic Press, New York (1985) |
| [40] | Ramezani, A., Alasty, A., and Akbari, J. Influence of van derWaals force on the pull-in parameters of cantilever type nanoscale electrostatic actuators. International Journal of Solids and Structures, 44, 4925-4941 (2007) |
| [41] | Alves, E., Ma, T. F., and Pelicer, M. L. Monotone positive solutions for a fourth order equation with nonlinear boundary conditions. Nonlinear Analysis, Theory, Methods and Applications, 71, 3834-3841 (2009) |
| [42] | Baghani, M., Jafari-Talookolaei, R. A., and Salarieh, H. Large amplitudes free vibrations and post-buckling analysis of unsymmetrically laminated composite beams on nonlinear elastic foundation. Applied Mathematical Modelling, 35, 130-138 (2011) |
| [43] | He, J. H. Variational iteration method-some recent results and new interpretations. Journal of Computational and Applied Mathematics, 207, 3-17 (2007) |
| [44] | He, J. H. and Wu, X. H. Variational iteration method: new development and applications. Com-puters and Mathematics with Applications, 54, 881-894 (2007) |
| [45] | Jafari, H., Saeidy, M., and Baleanu, D. The variational iteration method for solving nth-order fuzzy differential equations. Central European Journal of Physics, 10, 76-85 (2011) |
| [46] | Jafari, H. and Alipoor, A. A new method for calculating general la |
| [47] | Chang, J., Min, B. K., Kim, J., Lee, S. L., and Lin, L. Electrostatically actuated carbon nanowire nanotweezers. Smart Materials and Structures, 18, 065017 (2009) |
| [48] | Lin, W. H. and Zhao, Y. P. Dynamics behavior of nanoscale electrostatic actuators. Chinese Physics Letter, 20, 2070-2073 (2003) |
| [49] | Ramezani, A., Alasty, A., and Akbari, J. Analytical investigation and numerical verification of Casimir effect on electrostatic nanocantilevers. Microsystem Technologies, 14, 145-157 (2008) |
 2014, Vol. 35
2014, Vol. 35