1 Introduction
Low thermal conductivity is a primary limitation in the development of energy coefficient
heat transfer fluids required in many industrial and commercial applications. To get rid of such
issue,a new class of nanofluids has been developed. These fluids are the mixtures of traditional
fluids with nanoparticles. It was experimentally demonstrated that the resulting heat
transfer nanofluids have significantly higher thermal conductivity than the traditional fluids.
The nanofluids are the material through traditional liquids subject to suspended nanoparticles.
Metallic or nonmetallic nanometer sized particles are used as the nanoparticles. In particular,
the nanofluids have a pivotal role in advanced cooling systems,micro/nano electromechanical
devices,and thermal management systems via evaporators,heat exchangers,and industrial
cooling applications. Several researchers at present are now engaged to model and simulate
the flows of nanofluids. Some recent contributions in this direction may be found in Refs.
[1, 2, 3, 4, 5, 6, 7, 8, 9, 10] and the references therein. Moreover,it is well recognized that several fluids in industry
and engineering are non-Newtonian in nature. The well-known Nevier-Stokes equations do not
predict the rheological characteristics of non-Newtonian materials. Further,one constitutive relationship cannot describe the flow behaviors of all non-Newtonian fluids. Hence,several models
of non-Newtonian fluids were used[11, 12, 13, 14, 15]. The Casson fluid[16] is one of the non-Newtonian
materials predicting the shear thinning liquid (e.g.,blood,Jelly,concentrated fruit juices,etc).
It has been noted that not much has been reported about the flow of non-Newtonian fluids
with nanoparticles. Hence,the main aim of the present paper is to address the flow of the
Casson fluid in the presence of nanoparticles. The Brownian motion and thermophoretic effects
are presented. The flow considered is due to the stretching cylinder. The nonlinear problem is
computed and studied.
2 Problem development
The axisymmetric flow of an incompressible Casson fluid with nanoparticles is examined.
The behaviors of the Brownian motion and thermophoresis are also considered. The stretchable
cylinder is along the horizontal axis,i.e.,the x-axis. Here,the r-axis is taken along the radial
direction. The velocity,temperature,and concentration fields through the boundary layer
approximations satisfy the following equations:
where
u and
v represent the velocity components along the
x- and
r-directions,respectively,
U0 is the reference velocity,
β =${{{\mu _B}\sqrt {2{\pi _c}} } \over {{\tau _r}}}$ is the material parameter,in which
μB is the plastic
dynamic viscosity,
τr is the yield stress of fluid,and πc
is the critical value of this product
based on the non-Newtonian model,
l is the characteristic length,τ = (
ρc)
p/(
ρc)
f is the ratio
between the effective heat capacity of the nanoparticle material and heat capacity of the fluid
with
ρ being the density,
DB is the Brownian diffusion coefficient,
DT is the thermophoretic
diffusion coefficient,
σ is the thermal diffusivity of the fluid,
cp is the specific heat at the constant
pressure,
Cw is the concentration susceptibility,
Tw is the wall temperature,
ν is the kinematic
viscosity,and
k is the variable thermal conductivity of the fluid defined as
We introduce the following nondimensional quantities:
By Eq. (7),Eq. (1) is identically satisfied,and Eqs. (2)-(5) yield
where
γ =$\sqrt {{{lv} \over {{a^2}{U_0}}}} $is a curvature parameter,
Pr =${\nu \over \sigma }$ is the Prandtl number,
Nb=τ${{{D_B}} \over \nu }$ (
Cw-
C∞)
is the Brownian motion parameter,N
t =${{\tau {D_T}\left( {{T_W} - {T_\infty }} \right)} \over {{T_\infty }\nu }}$is the thermophoretic parameter,
Ec = ${{U_0^2{{\left( {x/l} \right)}^2}} \over {{c_p}\left( {{T_W} - {T_\infty }} \right)}}$is the Eckert number,and
Le =${\nu \over {{D_B}}}$ is the Lewis number. The local Nusselt number
Nux and the Sherwood number
Shx are defined as
The dimensionless form of the local Nusselt number
Nux is
The dimensionless form of the Sherwood number
Shx is given by
3 Homotopy analysis solutions
The initial approximations and auxiliary linear operators are chosen in the forms of
subject to
where
Ci (
i = 1,2,· · · ,7) are the arbitrary constants determined from the boundary conditions.
If
p ∈ [0,1] denotes an embedding parameter,and
hf,
hθ,and
hφ are the non-zero auxiliary
parameters,then the zeroth-order deformation problems are
where
Nf,
Nθ,and
Nφ are the nonlinear operators defined by
When
p = 0 and
p = 1,
and when
p varies from 0 to 1,
f(
η;
p),
θ(
η;
p),and
φ(
η;
p) vary from
f0(
η),
θ0(
η),and
φ0(
η)
to
f(
η),
θ(
η),and
φ(
η),respectively. Now,
f,
θ,and
φ in Taylor’s series can be elaborated as
follows:
where the convergence depends upon
hf,
hθ and
hφ. By proper choice of
hf,
hθ,and
hφ,the
series (28)-(30) converge for
p = 1. Hence,
The mth-order deformation problems are given by
The general solutions of Eqs. (35)-(37) are
where f
m*,
θm*,and
φm* are the special solutions of Eqs. (43)-(45).
We know that the homotopy analysis method (HAM)[16, 17, 18, 19, 20] solution highly depends upon
the non-zero auxiliary parameter ħ which helps us to adjust and control the convergence region.
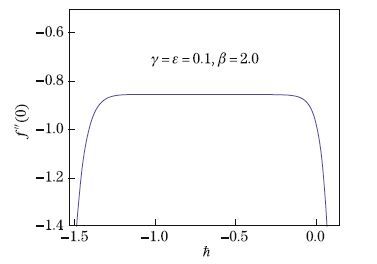
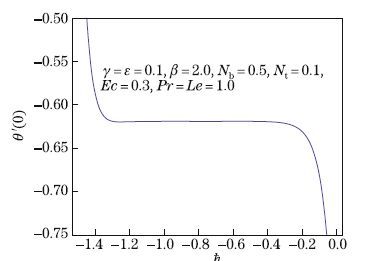
Therefore,we draw the ħ-curves for f''(0),θ'(0),and φ'(0). Figures 1-3 depict the ħ-curves for
different values of embedded parameters. The suitable range of ħf is -1.2 < ħf < -0.2,for ħθ,it is -0.5 < ħθ < -0.8,and for ħφ,it is -0.8 < ħφ < -1.2. It is found that the HAM solutions
converge entirely when ħf = -0.8,ħθ = -1.2,and hφ = -1.2. Table 1 shows the convergence of
series solutions. It is evident that the 20th-order estimations are enough for convergent series
solutions.
Table 1 Convergence of HAM solutions for different orders of approximations
4 Results and discussion
This section discloses the salient features of different physical quantities involved in the
temperature and concentration fields. The temperature profile is drawn in Fig. 4 for various
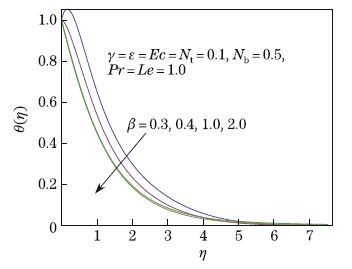
values of Casson fluid parameter β. The temperature profile decreases with the increasing η
for given values of β. It is shown that the Casson fluid parameter is inversely proportional
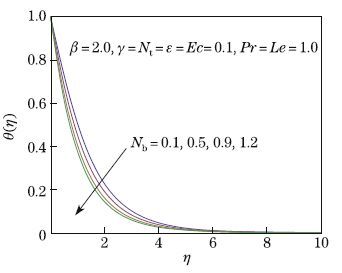
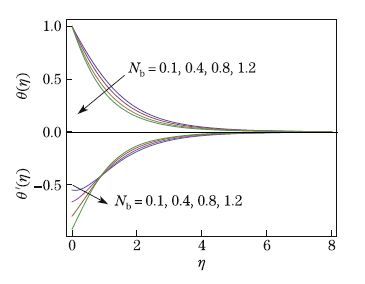
to the yield stress. The variation of the temperature with η is calculated for different values of Brownian motion parameter Nb in Fig. 5. When Nb increases,both the temperature and
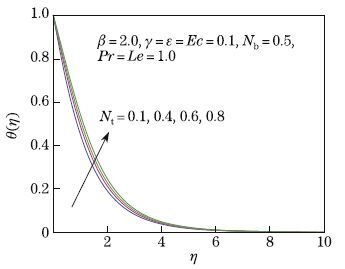
the thermal boundary layer thickness decrease. Figure 6 depicts the effect of thermophoretic
parameterNton the temperature profile. This figure shows thatNtenhances the temperature
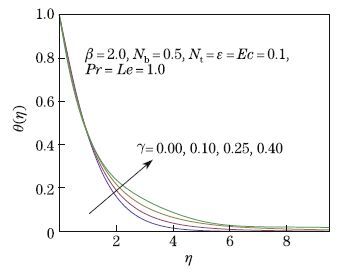
field. Figure 7 plots the influence of γ on the temperature field. The effect of γ near the wall is
almost negligible,while when η > 1,the temperature increases. Figure 8 explains the variation
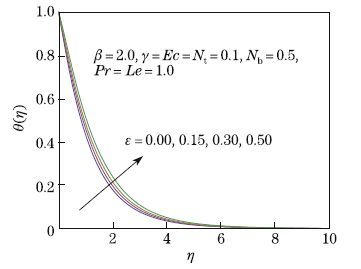
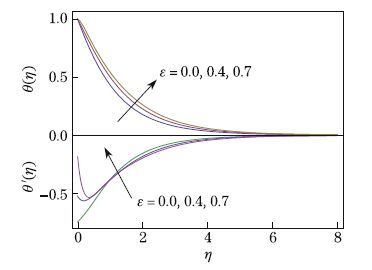
of variable thermal conductivity parameter ε on the temperature profile. It is noted that
θ(η) for the constant thermal conductivity case is less than the variable thermal conductivity.
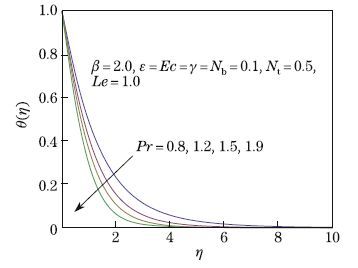
Figure 9 describes the variation of Pr on the temperature field. This figure illustrates that the
temperature field decreases when Pr increases. The effect of the Casson fluid parameter β on
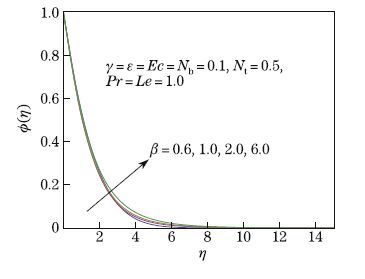
φ(η) is shown in Fig. 10. This indicates that φ(η) is an increasing function of the Casson fluid
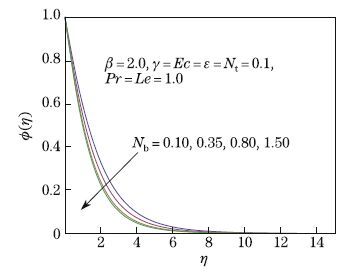
parameter β. Figure 11 displays the influence of the Brownian motion parameter Nb on φ(η).
The concentration field decreases very slowly when the Brownian motion parameter increases.
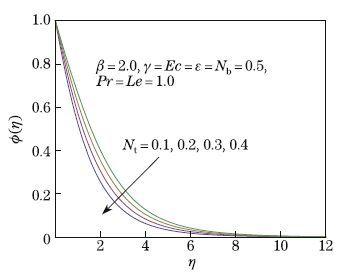
The enhancement in the thermophoretic parameterNtleads to an increase in the concentration
field. Also,the boundary layer thickness is more pronounced (see Fig. 12). The effect of Le
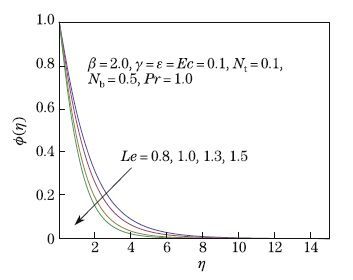
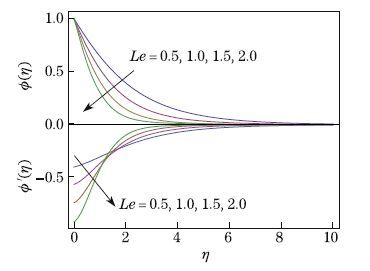
is depicted in Fig. 13. The concentration field and the associated boundary layer thickness
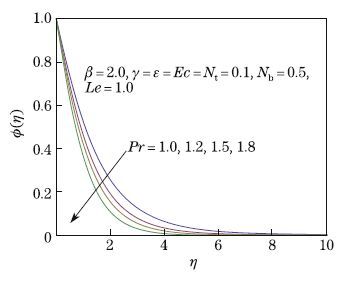
are decreasing functions of Le. The Prandtl and Lewis numbers have similar effects on the
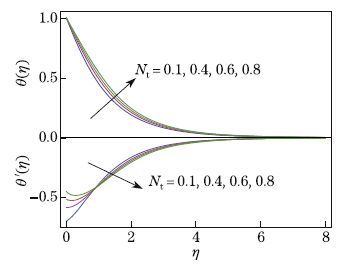
concentration (see Fig. 14). Figure 15 illustrates the impact of temperature and temperature
gradient for different values of Nt. The temperature increases for larger values of Nt,whereas
the temperature gradient increases most rapidly near the wall,but when η > 1,it decays
very slowly and then vanishes far away. The temperature gradient decreases near the cylinder
surface when the fluid thermal conductivity increases (see Fig. 16). Figures 17 and 18 present
the effects of Nb and Le on the concentration and the concentration gradient,respectively. For
both parameters,the temperature and the temperature gradient decrease.
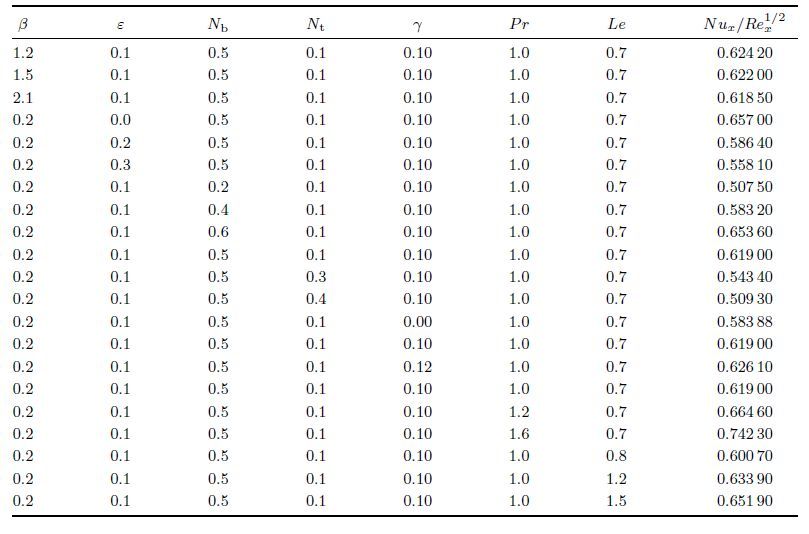
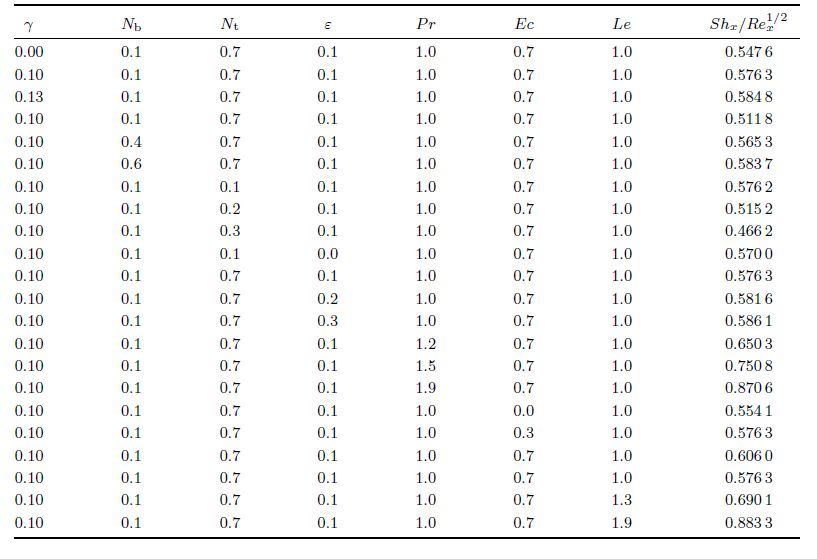
Table 2 depicts the numerical values of local Nusselt number for different values of β,ε,Nb,γ,
Pr,Le,and Nt. The increase in Nb,Pr,γ,and Le enhances the local Nusselt number. It is
also observed from this table that for larger values of β,ε,and Nt,the local Nusselt number
decreases. The numerical values of local Sherwood number are displayed in Table 3. The local Sherwood number at the wall decreases for larger Nb and Nt. The enhancement in β,ε,Pr,Ec,
and Le yields an increase in the local Sherwood number.
Table 2 Values of local Nusselt number Nux/Rex1/2
for different parameters
Table 3 Values of local Sherwood number Shx/Rex1/2for different parameters
5 Conclusions
This article addresses the flow of the Casson fluid with nanoparticles. The resulting problems
are computed successfully. It is found that the temperature and the thermal boundary layer
thickness are increasing functions of ε and Nt. However,Nb and γ have opposite behavior on
the temperature profile. Variable thermal conductivity enhances the fluid temperature,while
it decreases θ'(0) from the wall. Both the local Nusselt and local Sherwood numbers increase
with Le,whereas Nt has the opposite effect.

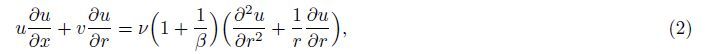

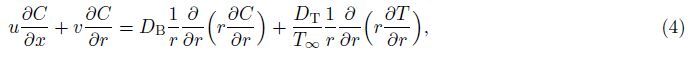
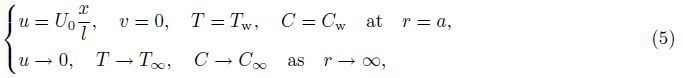

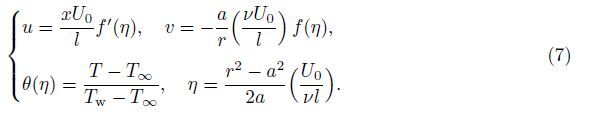
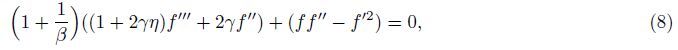
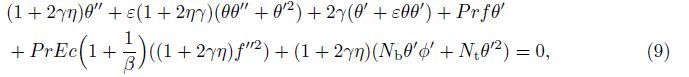
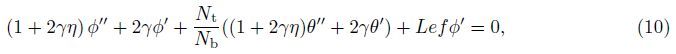
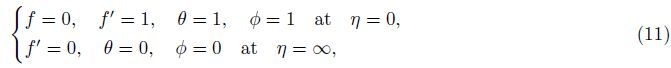
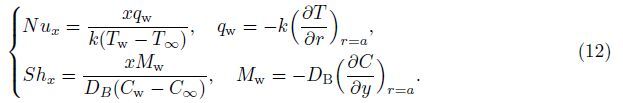


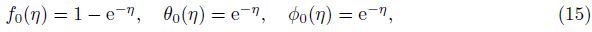
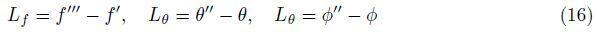



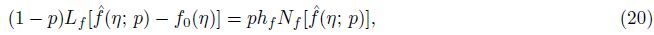
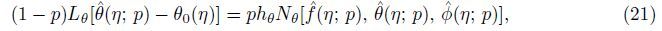
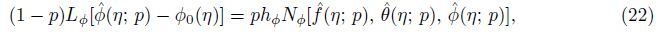
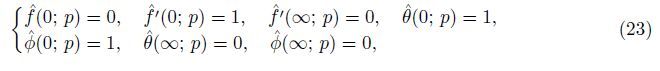
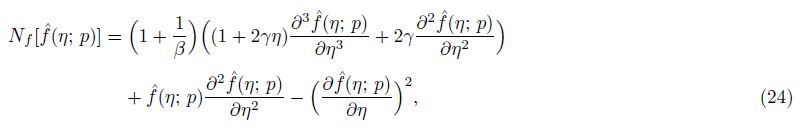
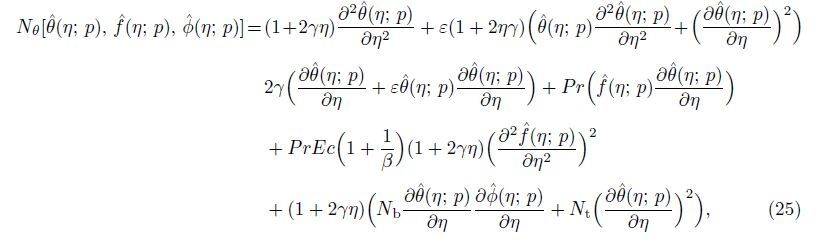
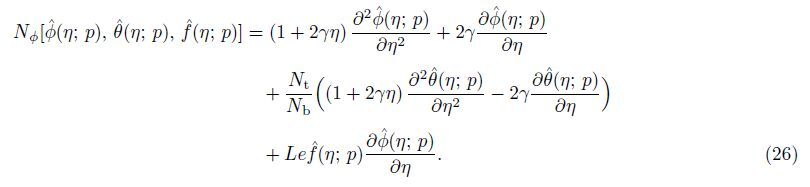
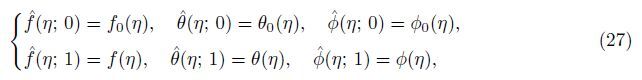
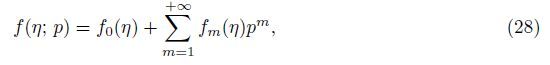
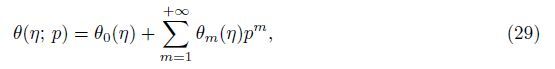
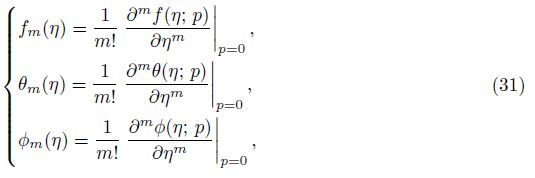


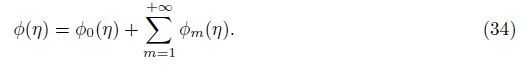



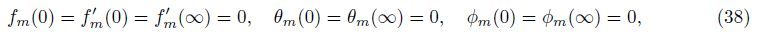
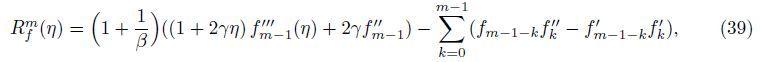
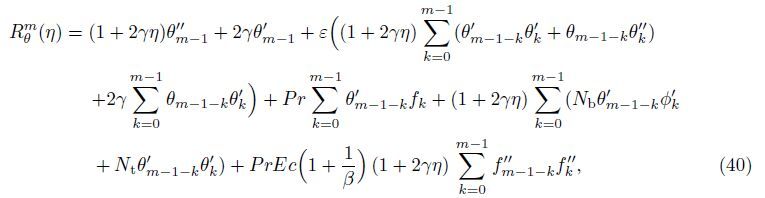
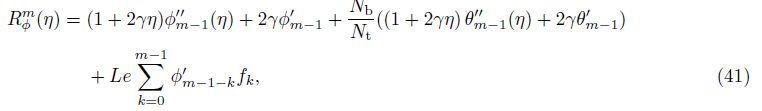

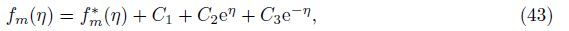
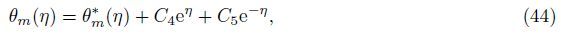
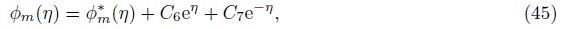
 2016, Vol. 37
2016, Vol. 37