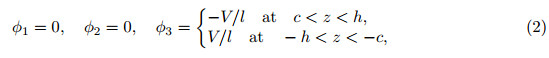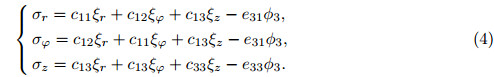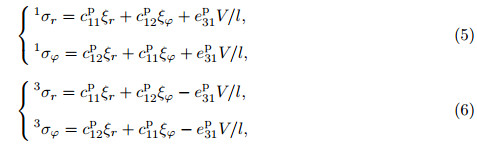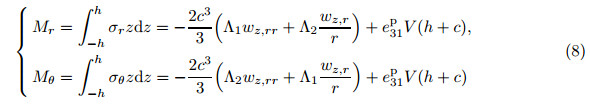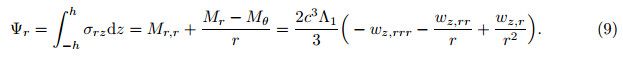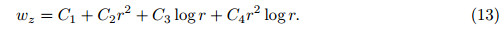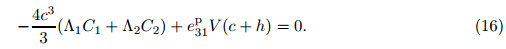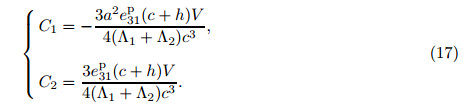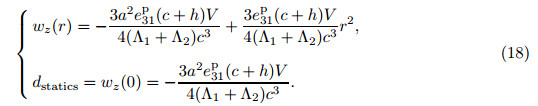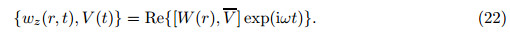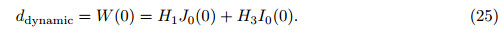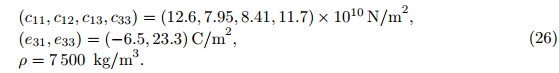Shanghai University
Article Information
- Hairen WANG, Ming HU, Zhenqin LI. 2016.
- Modelling and analysis of circular bimorph piezoelectric actuator for deformable mirror
- Appl. Math. Mech. -Engl. Ed., 37(5): 639-646
- http://dx.doi.org/10.1007/s10483-016-2077-8
Article History
- Received Jul. 25, 2015
- Revised Dec. 26, 2015
2. Key Laboratory for Radio Astronomy, Chinese Academy of Sciences, Nanjing 210008, China;
3. Institute of Geodesy and Geophysics, Chinese Academy of Sciences, Wuhan 430077, China;
4. School of Materials and Metallurgy, Northeastern University, Shenyang 110004, China
For the astronomy telescope of the earth,the light is distorted by the turbulence in the air when it travels through the atmosphere[1]. To compensate the atmospheric distortions, adaptive optics was invented. Adaptive optics that uses a deformable mirror (DM) as a key device,is a powerful tool for atmospheric seeing correction[2, 3]. The DM is typically supported by many actuators,which adjust the surface shape of the DM to compensate the light’s wave front error due to the atmospheric distortions[4]. Thus,the DM is a smart structure,and its shape could be precisely controlled by the adaptive system[5]. The bandwidth of adaptive optics system is decreased under the way of the closed-loop control[6]. However,the frequency range of the atmospheric turbulence is larger than 6 000 rad/s (about 103 Hz)[7]. The actual bandwidth of the precision adaptive optics system is usually limited by the resonant frequency of the DM[8]. Recently,the cost of the adaptive optics telescope is much more expensive because the aperture becomes larger and larger[9]. Therefore,the system of the adaptive optics telescope requires its actuators to have high speed,high accuracy,large stroke,large resonant frequency, and low cost. In the past 20 years,the piezoelectric actuator has received a great number of interests[10, 11, 12, 13, 14, 15, 16]. Due to piezoelectric actuators’ high accuracy and high speed,they have been widely used in many smart structures[5, 8, 17, 18, 19, 20, 21]. However,the piezoelectric actuators that are good candidates for making DMs of large telescopes are very few. Hence,we need to look for some new piezoelectric actuator structures which have large stroke,high resonant frequency, and low cost.
Here,a circular bimorph piezoelectric actuator (CBPA) is studied. The CBPA,whose structure is much simpler,may be a good candidate for the DM of the large astronomy telescopes. In Section 2,the model of CBPA is described,and the analytical solutions including the solution of statics and the solution of dynamics are described. The numerical calculation is carried out in Section 3,in which the dependence of the CBPA performance on the physical parameters is presented. In Section 4,some conclusions are obtained.
2 Analysis of CBPAThe CBPA consists of three layers (see Fig. 1). The top and the bottom lays are the identical piezoelectric materials,whose polarized direction and z-direction are accordant. The total actuator thickness is equal to 2h,and the metallic layer’s thickness is equal to 2c. The CBPA’s diameter is equal to 2a. The electrodes of the bottom and the top surfaces of the CBPA,which are in parallel,have the same voltage across. The middle metallic layer of the CBPA is shared as the third electrode by the other two piezoelectric ceramic layers. From Fig. 1(b),the CBPA is simply-supported at r = a,in which any in-plane displacement is prohibited. Once the CBPA is at an applied voltage V ,the bottom (top) piezoelectric layer will be driven to contract and the top (bottom) layer to extend. Thus,the voltage induces the circular bimorph structure into the flexure deformation. Figure 1(c) shows the dome height d,which is the distance from the horizontal plane to the center of the CBPA. The dome height d is also the deflection at r = 0. Figure 1(a) shows the measurement system,including linear variable differential transformer (LVDT),signal conditioner,digital to analog (DA) card,and computer,which will be connected to the center of CBPA in the future.
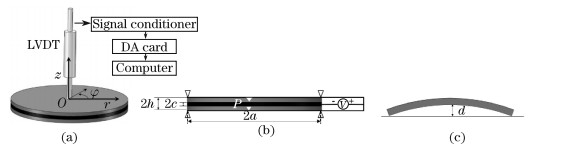 |
| Fig. 1 Schematic of simply supported CBPA |
In this part,the statics solution is derived in the cylindrical coordinate system. The r-direction is the radial direction,the ϕ-direction is the circumferential direction,and the z-direction is the longitudinal direction. Here,the flexural deformation of the CBPA is axis-symmetric. With the assumption of 2h/a <<1,the axially symmetrical deflection wz(r) of the CBPA can be expressed as follows:
Here,(r,ϕ,z) corresponds to (1,2,3). With the consideration of 2h/a << 1,the shear stresses are far smaller than the in-plane principal stresses. Hence,σ23 and σ31 are neglected[22, 23, 24]. According to the designs of the electrodes of the CBPA,we can obtain its electric fields where l = h − c,which is the thickness of the piezoelectric ceramic layer. The deflection of the CBPA is axis-symmetric,which requires and σ12 = 0 is obtained. In the light of polarized direction and c11 = c12,c13 = c23,e31 = e32, we can obtain the following constitutive relations of the CBPA: Assuming that the plate is thin,and the normal stress is vanished,we get the constitutive relations of the two piezoelectric layers as follows: where (c11p ,c12p) = (c11,c12)− (c132 ,c132 )/c33,and e31p = e31 − e33c13/c33. Besides,we also get the constitutive relations of the metal layer where c12m = νEm/((1 + ν)(1 − 2ν)),and c11m = c12m + Em/(2(1 − ν)). Em is the metallic Young’s modules,and ν is the metallic Poisson’s ratio. By integrating the principal stress over the thickness direction of the plates,we obtain the bending moments per unit length. From constitutive relations of the layers,we get with (Λ1,Λ2) = (c11m +γc11p ,c12m +γc12p ) and γ = (h/c)3 −1. With the integral of the shear stress over the dimension z of the CBPA,we can obtain the transverse shear force per unit length[25], With consideration of 2h/a <<1,we can obtain the following equilibrium equation[25]: From Eqs. (9) and (10),we get where ▽2 is Laplacian. Considering that the CBPA is simply-supported,we can obtain the boundary conditions, The general solution of Eq. (11) takes the following form: Here,C1 − C4 are four constants,which need to be determined. Considering that the value of deflection wz is finite at r = 0,we can obtain From the first equation of (12),we get From the second equation of (12),we obtain From Eqs. (15) and (16),we get From Eqs. (13),(14),and (17),we get 2.2 Dynamics solutionThe dynamic deflection is wz(r,t),and Eqs. (1)-(9) have the same formulas. With consideration of 2h/a << 1,we can obtain the motion equation,
and m = 2(ρ(h−c)+ρ'c),where ρ and ρ' are densities of the piezoelectric layer and the metallic layer,respectively. From Eqs. (9) and (19),we get where K = 2c3Λ1/3. Considering that the CBPA is simply-supported,we can obtain the boundary conditions of the dynamics, On account of harmonic motions,the notation of complex number takes the following form: The general solution of Eq. (20) can be obtained as with α4 = mω2/K,and J0(αr) and I0(αr) are a zeroth-order Bessel function and a zeroth-order modified Bessel function of the first kind,respectively. Y0(αr) and K0(αr) are a zeroth-order Bessel function and a zeroth-order modified Bessel function of the second kind,respectively. Since Y0(αr) and K0(αr) are infinite,we obtain H2 = H4 = 0,and Eq. (23) can be rewritten as[26] where H1 and H3 are two constants to be determined by Eq. (21). Once the constants are obtained,we can get 3 Numerical calculations and discussionIn order to evaluate the performance of the CBPA,some numerical calculations are carried out in the following. Here,PZT-5H is chosen as the piezoelectric material of the CBPA,and the parameters of the material are listed as follows[27]:
In the following,a = 30 mm,Δh = h − c = 5 mm,η = c/Δh = 1/2,and φ3 = 2 MV/m,unless stated otherwise. There are three potential choices for the metallic layer,which are shown in Table 1.Figure 2 shows the dependence of the dstatics upon the electric field φ3 for different metallic layers. The calculations are carried out by the linear piezoelectricity without consideration of the nonlinearity and the hysteresis. Therefore,the results are linear. The dstatics of the CBPA without a metal layer is larger than the others,because the CBPA with a metallic layer,whose bending stiffness is strengthened,results in a decrease in dstatics. Furthermore,the decreases of dstatics of the different metallic layers are different,depending on the material characteristics of the three kinds of metals. Figure 3 shows the dependence of the dstatics upon 1/η for three kinds of metallic layers. From Fig. 3,we can find that dstatics increases with increasing 1/η. It is observed that the dstatics of the CBPA with the Al layer is larger than that of the other two metallic actuators for the same 1/η,because the Al layer bending stiffness is smallest in the three kinds of metals. When 1/η increases larger than the value of 1/η = 15,three curves gradually become coinciding and flatter,which indicates that the thickness of metallic layers is too thin to have effects on dstatics.
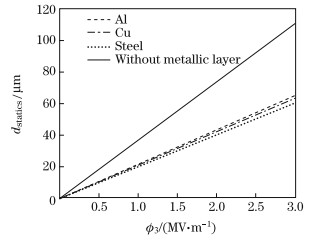 |
| Fig. 2 Dependence of dstatics upon electric field φ3 for different metallic layers |
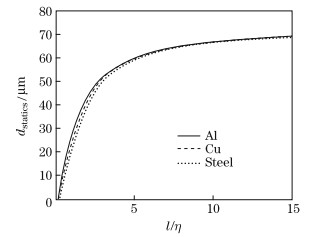 |
| Fig. 3 Dependence of dstatics upon ratios 1/η for three kinds of metallic layers |
Figure 4 shows the dependence of the ddynamic of the CBPA with the Al layer upon the driving frequency for the different ratios η. We can observe that the resonant frequency of the CBPA increases with increasing η. It can be found that the natural frequency of the CBPA without a metallic layer (η = 0) is the lowest. It suggests that the increase in η strengthens the bending stiffness of the CBPA,and therefore the resonant frequency becomes larger. From Fig. 4 and Fig. 2,it is observed that the ddynamic of ω = 0 is almost equal to the dstatics. The natural frequencies of the CBPA of the three kinds of metallic layers at η = 1/2 are shown in Fig. 5. It can be found that the natural frequency of the CBPA with the Al layer is larger than the natural frequency of the other two metal actuators. The reason for the result is that the natural frequency of the CBPA is a function of two variables: bending stiffness and mass. The CBPA of the Al metallic layer has the smallest bending stiffness,but the mass density of Al is the smallest,which makes the largest CBPA’s natural frequency. Thus,if we want to get a larger natural frequency,the CBPA with an Al metallic layer is preferable to the other choices.
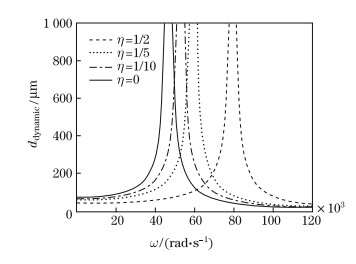 |
| Fig. 4 Dependence of ddynamic of different η upon driving frequency |
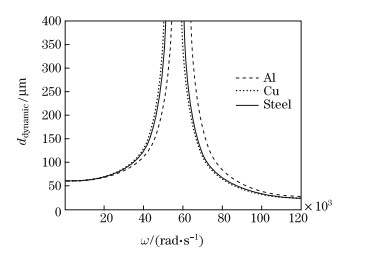 |
| Fig. 5 Dependence of ddynamic upon driving frequency for three kinds of metallic layers |
In this paper,a CBPA is proposed. The analytical solutions have been derived based on the linear theory of piezoelectricity. Some numerical calculations on the performance of the piezoelectric structure are carried out. The effects of physical parameters on the dstatics and the natural frequency of the CBPA are analyzed in detail. In the light of the specifications of the piezoelectric DM with a large natural frequency and a large stroke,the natural frequency of its piezoelectric actuator must be at least 6284rad/s (1000Hz) with a stroke of at least 10 μm. The numerical results suggest that the natural frequency of introducing the metallic layers into the bimorph is much larger than 6284rad/s,and the stroke of the CBPA easily satisfies the performance requirement. Furthermore,the cost of DMs could be cut down due to the simple structure of the CBPA. The obtained results in this paper are useful to the design of the piezoelectric actuators and the DMs.
| [1] | Schmutz, L. Adaptive optics: a modern cure for Newton tremors. Photon Spectra, 27, 119–128 (1993) |
| [2] | Babcock, H. W. The possibility of compensating astronomical seeing. Publications of the Astronomical Society of the Pacific, 65, 229–236 (1953) |
| [3] | Woolf, N. Adaptive optics. Proceedings of IAU Colloquium, Garching, Germany, 221–233 (1984) |
| [4] | Tyson, R. Principles of Adaptive Optics, CRC Press, Boca Raton (2010) |
| [5] | Hom, C. L., Dean, P. D., and Winzer, S. R. Simulating electrostrictive deformable mirrors I: nonlinear static analysis. Smart Materials and Structures, 8, 691–699 (1999) |
| [6] | Ning, Y. Performance Test and Application Study of a Bimorph Deformable Mirror (in Chinese), Ph.D. dissertation, National University of Defense Technology (2008) |
| [7] | Wilson, R., Franza, F., and Noethe, L. Active optics I: a system for optimizing the optical quality and reducing the costs of large telescopes. Journal of Modern Optics, 34, 485–509 (1987) |
| [8] | Hom, C. L. Simulating electrostrictive deformable mirrors II: nonlinear dynamic analysis. Smart Materials and Structures, 8, 700–708 (1999) |
| [9] | Lin, X. D., Xue, C., Liu, X. Y., Wang, J. L., and Wei, P. F. Current status and research development of wavefront correctors for adaptive optics. Chinese Optics, 4, 337–351 (2012) |
| [10] | Webber, K. G., Hopkinson, D. P., and Lynch, C. S. Application of a classical lamination theory model to the design of piezoelectric composite unimorph actuators. Journal of Intelligent Material Systems and Structures, 17, 29–34 (2006) |
| [11] | Hagood, N. W., Chung, W. H., and von Flotow, A. Modelling of piezoelectric actuator dynamics for active structural control. Journal of Intelligent Material Systems and Structures, 1, 327–354 (1990) |
| [12] | Hwang, W. S. and Park, H. C. Finite element modeling of piezoelectric sensors and actuators. AIAA Journal, 31, 930–937 (1993) |
| [13] | Goldfarb, M. and Celanovic, N. A lumped parameter electromechanical model for describing the nonlinear behavior of piezoelectric actuators. Journal of Dynamic Systems, Measurement, and Control, 119, 478–485 (1997) |
| [14] | Liu, L., Tan, K. K., Chen, S., Teo, C. S., and Lee, T. H. Discrete composite control of piezoelectric actuators for high-speed and precision scanning. IEEE Transactions on Industrial Informatics, 9, 859–868 (2013) |
| [15] | Vashist, S. K. and Chhabra, D. Optimal placement of piezoelectric actuators on plate structures for active vibration control using genetic algorithm. Proccedings of the SPIE, 9057, 905720 (2014) |
| [16] | Wang, H. R. Analytical analysis of a beam flexural-mode piezoelectric actuator for deformable mirrors. Journal of Astronomical Telescopes, Instruments, and Systems, 1, 049001 (2015) |
| [17] | Kamada, T., Fujita, T., Hatayama, T., Arikabe, T., Murai, N., Aizawa, S., and Tohyama, K. Active vibration control of frame structures with smart structures using piezoelectric actuators (vibration control by control of bending moments of columns). Smart Materials and Structures, 6, 448–456 (1997) |
| [18] | Crawley, E. F. and de Luis, J. Use of piezoelectric actuators as elements of intelligent structures. AIAA Journal, 25, 1373–1385 (1987) |
| [19] | Freeman, R. and Garcia, H. High-speed deformable mirror system. Applied Optics, 21, 589–595 (1982) |
| [20] | Wang, H. R., Hu, H. P., Yang, J. S., and Hu, Y. T. Spiral piezoelectric transducer in torsional motion as low-frequency power harvester. Applied Mathematics and Mechanics (English Edition), 34, 589–596 (2013) DOI 10.1007/s10483-013-1693-x |
| [21] | Wang, H. R., Xie, J. M., Xie, X., Hu, Y. T., and Wang, J. Nonlinear characteristics of circular-cylinder piezoelectric power harvester near resonance based on flow-induced flexural vibration mode. Applied Mathematics and Mechanics (English Edition), 35, 229–236 (2014) DOI 10.1007/s10483-014-1786-6 |
| [22] | Wang, H. R., Xie, X., Hu, Y., and Wang, J. Weakly nonlinear characteristics of a three-layer circular piezoelectric plate-like power harvester near resonance. Journal of Mechanics, 30, 97–102 (2014) |
| [23] | Wang, H. R., Hu, Y., and Wang, J. On the nonlinear behavior of a multilayer circular piezoelectric plate-like transformer operating near resonance. IEEE Transactions on Ultrasonics, Ferroelectrics and Frequency Control, 60, 752–757 (2013) |
| [24] | Yang, J. An Introduction to the Theory of Piezoelectricity, Springer, New York (2005) |
| [25] | Wang, J., Wang, H. R., Hu, H., Luo, B., Hu, Y., and Wang, J. On the strain-gradient effects in micro piezoelectric-bimorph circular plate power harvesters. Smart Materials and Structures, 21, 015006 (2012) |
| [26] | Huang, Y. and Huang, W. Modeling and analysis of circular flexural-vibration-mode piezoelectric transformer. IEEE Transactions on Ultrasonics, Ferroelectrics and Frequency Control, 57, 2764– 2771 (2010) |
| [27] | Auld, B. A. Acoustic Fields and Waves in Solids, Krieger Publishing Company, Malabar (1973) |
 2016, Vol. 37
2016, Vol. 37