Shanghai University
Article Information
- Yun PENG, Yadong WEI, Ming ZHOU
- Efficient modeling of cable-pulley system with friction based on arbitrary-Lagrangian-Eulerian approach
- Applied Mathematics and Mechanics (English Edition), 2017, 38(12): 1785-1802.
- http://dx.doi.org/10.1007/s10483-017-2284-8
Article History
- Received Jan. 15, 2017
- Revised May. 22, 2017
2. School of Aerospace Engineering, Tsinghua University, Beijing 100084, China
Cable-pulley systems are extensively used in engineering, such as cranes, the five-hundred-meter aperture spherical radio telescope (FAST)[1], mechanical experiments[2], robots and large space deployable antennas[3-4], some of which are shown in Fig. 1. In these applications, the cable is usually reeled in or paid out by a motor to drive a target so that the cable length can be changed. Moreover, the cable often passes over pulleys to change its direction, and the cable length is generally several orders of magnitude larger than the pulley size. In real cases, friction exists between the bearing and the pulley shaft and between the cable and the pulley surface, resulting in a decrease in the cable tension from the active side to the passive side, which is called the tension decay phenomenon. The tension decreases exponentially with the number of the pulleys passed over and thus may have significant effects on the dynamics of the system. For example, in large deployable antennas[4], an active cable is used for deployment, and the cable tension far from the motor is less than one tenth of that near the motor after passing over tens of pulleys, even though the friction coefficient is low. On the other hand, the friction between cable and pulley could be used to resist vibration such as in the Maryland rigging[5]. Therefore, the variable length and the cable-pulley friction should be taken into account in modeling of the cable-pulley system.

|
| Fig. 1 Typical applications of cable-pulley system |
|
|
Methods of the static and dynamic analysis of cable and its structure have been widely studied[6-12]. In recent two decades, researchers started to pay attention to the system with a variable-length cable. Kamman and Huston[13-14] proposed a discrete lumped mass model of cable link to simulate a ship towing system and a variable length link whose length can be actively changed near the towing point to model the pay-out/reel-in process. Williams and Trivailo[15] and Williams et al.[16] also used the same method to model a circularly towed aerial cable system and a kite, respectively. Du et al.[17] developed a continuous cable element with the variable length to investigate cable-driven parallel manipulators. These methods demand that the length of the cable elements must be changed actively, but not passively, i.e., they fail to model the case in which the stowing velocity is unknown, for example, a force is used to reel in the cable. Therefore, a more general continuous cable element whose length can be changed both actively and passively is needed.
With respect to the cable-pulley system, physically, the cable keeps in contact with pulleys if it is tensioned, as shown in Fig. 2(a). A natural thought of modeling the cable-pulley friction is the elastic contact formulation based on the Hertzian theory[18]. In this method, the size of the cable mesh should be smaller than the pulley radius for validation of the contact detections. A large number of meshes are then necessary in dynamical simulation when a long part of cable potentially comes in contact with small pulleys. As a result, the calculation time increases dramatically for both detecting potential contacts and solving governing equations. Thus, a more efficient modeling approach is necessary for engineering applications.

|
| Fig. 2 Three approaches of modeling cable passing through pulley |
|
|
Recently, researches addressed the contact between a long cable and small pulleys from another point of view. If the friction is not accounted, the main effect of the contact is to restrict pulleys to sliding along the flexible cable. One modeling approach is to mesh the cable with Lagrangian elements and add sliding constraints between a pulley and the cable elements, referred to as a sliding joint. The sliding joints on a beam were investigated by Seo et al.[19], Sugiyama et al.[20], and Lee et al.[21], based on the absolute nodal coordinate formulation (ANCF). As shown in Fig. 2(b), these sliding constraints introduce a non-generalized arc-length parameter to determinate the location of the joint along the beam element, which is used to construct the sliding constraint equations. These methods successfully avoid huge potential contact detections. However, they could not be applied to the case of a cable because the sliding joint would generate a force and dramatically change the corresponding element shape, for which its shape functions fail to describe.
This drawback is potentially bypassed once the mesh and the material do not coincide together so that the mesh can be dynamically adjusted as the sliding joint moves, as schemed in the arbitrary-Lagrangian-Eulerian (ALE) description[22]. Recently, Hong and Ren[23] combined the ALE formulation into the multi-body system to model a sliding joint on a flexible beam, the axis mass flow[24], and the drilling system[25]. Based on the ALE method, they developed a length-variable ANCF beam element and used it to formulate a novel sliding joint[23], as shown in Fig. 2(c). The basic idea was to add the arc-length parameter into the nodal generalized coordinate. Therefore, an ALE beam node could be considered as sliding along the beam. However, this ALE beam element could not be directly applied to the cable-pulley system because the slope of beam element is continuous while that of the cable element is discontinuous as the cable cannot resist bending. Therefore, a new ALE cable element is in need. More importantly, modeling of the friction between the sliding joint and the cable has not been investigated.
Based on the background described above, this paper proposes an efficient approach for modeling the cable-pulley system with friction based on the ALE formulation. A two-node ALE cable element is formulated in detail. Compared with the ALE beam element in Ref.[23], this element eliminates slope coordinates from the nodal generalized coordinates. Therefore, it is more efficient and effective. Modeling of the cable-pulley friction is then investigated. The law of tension decay phenomenon resulting from the cable-pulley friction is derived and embedded in the multi-body system modeling. A transitional ALE element, whose two nodes are constrained to two corresponding locations of the pulley, is proposed to model the contact part of the cable. The modeling of the tension decay phenomenon is derived as a simple expression of the generalized friction force acting only on the arc-length coordinates of the transitional element.
The rest of the paper is organized as follows. Section 2 presents the ALE cable element and the modeling methods of cable passing over pulleys and of the tension decay phenomenon resulting from the cable-pulley friction. Section 3 offers three examples to verify the proposed method, and Section 4 concludes the study.
2 Modeling cable and its friction with pulleyThis section presents the modeling method of the cable-pulley system with friction, in which a cable passes over multiple pulleys and is also reeled in or paid out by motors at the cable ends, as shown in Fig. 3. A new ALE cable element is presented to model the cable. Compared with the ALE beam element[23], the slope coordinates of this cable element can be discontinuous, making it more efficient and effective. A transitional ALE element, whose two nodes are fixed to two corresponding locations of pulley, is proposed to model the contact part of pulley. The cable passing over pulley can be seen as decreasing the length of the cable element at one side and increasing the element length at the other side, enabling the cable mesh to automatically adapt to the movement of the cable. As a result, the cable can be meshed roughly, and the contact detections are avoided, significantly speeding up the calculation. In the following subsections, the ALE cable element is firstly presented in detail; the cable-pulley friction is then derived as a simple law of tension decay phenomenon; finally the corresponding modeling method is proposed.

|
| Fig. 3 Illustration of cable-pulley system and ALE cable mesh |
|
|
As schemed in Fig. 4, the ALE cable element contains two ALE nodes. The generalized coordinate qk of the kth cable node is

|
| Fig. 4 Linear ALE cable element of two nodes |
|
|

|
(1) |
where rk is the nodal global position vector, sk is an arc-length parameter measured along the cable from the head point, and the superscript T is the transpose of vector. Introducing the arc-length coordinate allows the node to be movable along the cable. The head point can be defined as any point on the cable, such as one fixed end.
If the special constraint is imposed on an ALE node, it could be degenerated to an Eulerian or a Lagrangian node. An Eulerian node is fixed to the ground but its arc-length coordinate can vary. Therefore, the constraint equation is r − r0 = 0. While a Lagrangian node owns a constant arc-length coordinate, realized by s − s0 = 0.
In this framework, the generalized coordinate vector of the element is
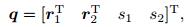
|
(2) |
where the subscript 1 or 2 refers to the index of the node. The length of the element is

|
(3) |
which can vary with time.
The global position r of any point inside the element is determined by introducing a linear interpolation,

|
(4) |
where N1 and N2 are the shape functions, and ζ is the local nature coordinate of the isoparametric element. The parameter ζ has a relationship with the arc-length coordinates,
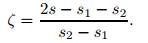
|
(5) |
Note that ζ is the time variable. Therefore, the shape functions are time-dependent.
For convenience, the position of any point in the element is rewritten in the vector format,

|
(6) |
where I3 is the three-dimensional identity matrix.
The velocity and acceleration of any point in the element are obtained by the first and second derivatives of the position with respect to the time. Since the shape function is time-dependent, they should be deduced as follows:

|
(7) |
The time differentiation of the shape function is given by

|
(8) |
Therefore, Eq.(7) can be given in a concise form,

|
(9) |
where the additional acceleration 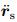
According to the principle of virtual work, the sum of virtual work done by the external force, elastic force and inertia force should be zero at any moment,

|
(10) |
where δWf, δWe, and δWi denote the virtual work of external, elastic, and inertial forces, respectively. These terms are

|
(11) |
with

|
(12) |
where f(s, t) is the external force, E is Young's modulus, A is the cross-sectional area, ρ is the density, ε is the axial Green strain of the cable element, k is introduced as the cable can resist only tension but not compression, and β is the stiffness proportional Rayleigh damping factor. Note that this is a linear element. Therefore, the strain is uniform along the element. However, the strains and the cable tensions of two neighboring elements can be different.
The governing equation of the cable element is obtained as follows:

|
(13) |
with

|
(14) |
where Mele is the generalized mass matrix, Qp is the additional inertial force, Qe is the generalized elastic force, and Qf is the generalized external force. The additional inertial force Qp would become zero if the element is degenerated to a Lagrangian element.
2.1.3 Property of mass matrixUnlike the conventional Lagrangian cable element, the mass matrix Mele here is not constant. According to Eqs.(9) and (14), it is composed of 3×3 blocks,

|
(15) |
Even when the element is degenerated to a Lagrangian element, the first block of NeTNe is constant, but the rest blocks can vary as qe is variable, leading to that the mass matrix remains time-dependent.
2.2 Cable passing over pulley with frictionAs shown in Fig. 5(a), the cable-pulley friction causes that the cable tension decreases from the active side to the passive side. Here, a transmission factor is proposed to indicate this tension decay phenomenon,

|
| Fig. 5 Sketches of (a) transitional factor and (b)-(d) three types of pulley supports, i.e., fixed to base, supported by journal bearing and rolling bearing, respectively |
|
|

|
(16) |
where η≤1, T1 is the tension at the active side, and T2 is the tension at the passive side. Therefore, the friction force is ft=(1-η)T1. The cable tension is obtained from

|
(17) |
Next, the transmission factor η is studied according to different types of pulley support, and then modeling of the friction is presented.
2.2.1 Transmission factorTheoretically, the transmission factor η is determined by many factors, such as the friction coefficient between pulley and cable/bearing, the contact angle θ, and the pulley radius. Generally, there are three types of pulley support, fixed to the base, supported by a journal bearing and a rolling bearing, as shown in Figs. 5(b)-5(d). In the following, we will briefly show that η, in all of these supports, is mainly decided by the contact angle θ.
In the first type, when the pulley is fixed to the base, the cable is slipping over the pulley, as shown in Fig. 5(b), and the transmission factor is written as[26]

|
(18) |
where μ is the friction coefficient, and θ is the contact angle around pulley.
In the other two types, there is no relative movement between the cable and pulley. The tension decay is caused by the friction force of the journal bearing and the friction torque of the rolling bearing, respectively. For the case of the journal bearing, as shown in Fig. 5(c), the normal force N acting on the journal is the amount of vector sum of the cable tensions at two sides,
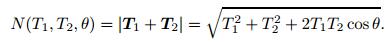
|
(19) |
As the pulley inertia is generally negligible, the equilibrium of the pulley gives

|
(20) |
where rp and rj are the radii of pulley and journal, respectively. By combining Eqs.(16), (19), and (20), and eliminating the terms T1 and T2, the equation for the factor η is obtained as

|
(21) |
in which α=rp/(μrj). Given η≤1, it is obtained as

|
(22) |
For the case of the rolling bearing, the deduction is similar, and the formula of η is the same, but with the coefficient α=rp/(fdd), where fd is the friction moment coefficient similar to μ, and d is the diameter of the rolling bearing, as indicated in Fig. 5(d).
Both Eqs.(18) and (22) show that the transmission factor is a function of the contact angle θ. Besides, the transmission factor is also influenced by the radius of the pulley as indicated by α in Eq.(22). However, for a given pulley, the radius is fixed, and its influence is not considered thereafter. Therefore, the transmission factor η is only determined by the angle θ and can be easily integrated into the multi-body system. By the way, the factor can be considered as a constant if the angle θ varies little.
2.2.2 Transitional element methodAs shown in Fig. 6(a), a transitional ALE element is proposed to model the contact part of the cable with the pulley. The positions of its two nodes are attached to the two corresponding locations of the pulley, respectively. Therefore, the constraint equations are

|
(23) |
where ri is the global position of the ith ALE node, the subscript c represents the pulley center, and u is the local position of points on the pulley relative to the pulley center. Note that the arc-length coordinates are not fixed. Therefore, the pulley can slide along the cable. It is worth mentioning that the contact points between cable elements and the pulley might change slightly with the movement of the cable. However, it is reasonably neglected here because the pulley size is generally much smaller than the cable length.
As shown in Fig. 6(b), the friction force is presumptively distributed on the transitional element as

|
| Fig. 6 Sketches of (a) transitional element method, (b) friction force distributed on transitional element, and (c) reaction friction force distributed on pulley |
|
|

|
(24) |
where ft is the amount of friction force, Li is the length of the transitional element, and t is the unit direction vector between the two ALE nodes. According to Eq.(14), the generalized force Qfi of friction on the two nodes is

|
(25) |
which indicates that the friction produces the generalized force ftt/2 on the global position and -ft/2 on the arc-length coordinate of each node. Meanwhile, a reaction friction force ft'=-ft is also exerted on the pulley, as shown in Fig. 6(c). Therefore, the governing equations of the ALE cable element and the pulley are

|
(26) |
where Q is the pre-existing generalized force, and λ is the constraint force of Eq.(23). Apparently, the friction force and the constraint force act together. By defining

|
(27) |
the first three formulae of Eq.(26) can be rewritten as

|
(28) |
This means that the generalized friction force of global position on the ALE nodes and on the pulley could combine with the original constraint force to form a new equivalent constraint force, and there is no difference for the variables r and s. Thus, the generalized friction is formulated as

|
(29) |
This simple expression shows that the friction force introduces the generalized force acting only on the arc-length coordinates, which is independent of the global positions and is irrelevant to the direction t.
2.2.3 One ALE node methodIn real engineering, the pulley size is often several orders of magnitude smaller than the cable length and thus can be negligible. Therefore, the transitional element could be degenerated to a single ALE node. In this case, the constraint equation is modified as

|
(30) |
Similarly, the generalized friction force acting on this ALE node is the resultant force of Eq.(29) on the two nodes,

|
(31) |
which acts on the arc-length coordinate of this one ALE node, and the magnitude is equal to the amount of the friction force. Besides, this friction generalized force will lead to that the cable tensions of the two neighboring elements are different, which will be further discussed in Example 2.
2.3 Governing equations of whole systemFor a system composed of the cable, pulleys and other rigid/flexible bodies[27], as shown in Fig. 3, the system generalized coordinate vector q consists of the generalized coordinates of all bodies,

|
(32) |
where qc is the generalized coordinate vector of cable, qb is the generalized coordinate vector of rigid and flexible bodies, the subscript r refers to rigid, f refers to flexible, and N, m and n are the numbers of cable nodes, rigid bodies, and flexible bodies, respectively.
By assembling the motion equations of all bodies, constraints and forces, the governing equations of the whole system are written in the standard form for the multi-body system,

|
(33) |
where M(q, t) is the mass matrix of system, 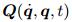
In this section, three examples are used to verify the accuracy and high efficiency of the proposed method. Example 1 simulates a simple cable-pulley system and verifies the proposed method by comparing it with the contact detection method, showing that the proposed method is over 100 times faster. Example 2 models a planar pendulum on a suspended cable and validates the proposed method with the analytical results. Example 3 is an application of the proposed method in a real engineering application.
3.1 Example 1: simple cable-pulley system with frictionThis example uses the contact detection method[18] and the proposed method to model a simple cable-pulley lift system, whose parameters are shown in Fig. 7. In the contact detection model, the cable passing through the pulley is modeled by contact detections between Lagrangian cable elements and a cylinder, as shown in Fig. 8(a). The cable element size is 1/40 of the pulley perimeter for validation of the contact detection. The Hertzian contact force consists of the normal contact force and the tangential friction force (see Ref.[18]),

|
| Fig. 7 Diagram of simple cable-pulley system |
|
|

|
| Fig. 8 Results of two modeling methods |
|
|

|
(34) |
where n is the contact normal unit vector, t is the slip direction, δ is the contacting penetration, k is the spring coefficient, the exponent γ produces a nonlinear contact force, and μ is the friction coefficient. This example uses the following parameters: k=7×106 N/m, γ=1.2, and μ=0.1.
In the proposed model, the cable is meshed with only two ALE elements and three ALE nodes, as shown in Fig. 8(b). The middle node which is degenerated to an Eulerian node is attached to the pulley center. Given μ=0.1 and the contact angle θ=π/2, the transmission factor for the proposed method is η=e-μθ=0.855.
The physical simulation time is 9 s. At t=0 s, the motor starts to reel in the cable with a constant velocity 0.5 m/s, and the gravity begins to take effect. Therefore, it is a dynamical transition at first, and then becomes a steady state. Figure 8(c) shows the results of the cable tensions of two methods. They pretty agree with each other in both the dynamical and steady processes.
The comparison of the two methods is listed in Table 2, showing that the proposed method is over 100 times faster than the contact detection method. This is benefited from the two advantages, i.e., the proposed method decreases the total degrees of freedom (DOFs) to about 2% of the contact method, and the large number of contact detections is avoided. These advantages will be significantly magnified if more pulleys are involved and the cable gets longer.
As shown in Fig. 9(a), a planar pendulum, with a pulley at the upper end, is released from rest and then slides with friction along a suspended cable under the gravity. The parameters of this example are shown in Fig. 9(a). An analytical model is presented in Appendix A, and its results are compared with numerical results of the proposed method. In simulation, the pendulum is modeled by a rigid body, and the cable is meshed with fourteen Lagrangian nodes and one ALE node. The pulley size is neglected for simplicity, and the ALE node is attached to the upper end of the pendulum. Two cases of different transmission factors are studied, η=1.00 and η=0.99. The former means friction-free, and the latter one is low-friction. Figure 9(b) shows the dynamical response of the system of η=0.99. The results show that the contact angle of the cable with the pulley is [116.5°, 121.8°]. Therefore, it is reasonable to choose a constant transmission factor.

|
| Fig. 9 Sliding pendulum on cable, (a) parameters of system and (b) simulation movement of system during half period of η=0.99 |
|
|
As plotted in Fig. 10, the results of pendulum angles and cable tensions of analytical and numerical models agree well, validating the accuracy of the proposed method. Figures 10(c) and 10(d) show that the cable tension of the left side is equal to that of the right side for η=1.00, since both the gravitional and the inertia forces of the cable are negligible compared with the gravity of the pendulum. However, for η=0.99, the friction causes a difference in the cable tension on the two sides, and their curves alternatively cross each other. The results also show that a small friction has an obvious effect on the dynamics of the system.

|
| Fig. 10 Results of numerical and analytical models, pendulum angles of (a) η=1.00 and (b) η=0.99 and cable tensions of (c) η=1.00 and (d) η=0.99 |
|
|
This example applies the proposed method to a real engineering problem, pendulation suppression of the Maryland rigging system[5] used in a shipboard crane, as shown in Fig. 11(a). The regular waves of the sea make the ship roll, pitch and heave forward and backward, exciting motion of the crane load. If the frequency of the waves is close to the natural frequency of the pendulum of the load, resonance will happen and dramatically swing the load, leading to the danger of collisions between the load and the ship.

|
| Fig. 11 (a) Maryland rigging system and (b) parameters of model |
|
|
The Maryland rigging system[5] uses friction, introduced by a pulley-brake assembly, and a length-controlled driving cable to suppress the swing of the load, as shown in Fig. 11(a). The parameters of the system are outlined in Fig. 11(b). This example assumes that the load mass is much smaller than the ship mass so that the movements of the ship and the load are uncoupled. The roll of the ship is considered as the displacement excitation of the load, and the angle is given as

|
(35) |
where β0=45° is the angle at the steady state, and β'(t) is a chaotic signal, as shown in Fig. 12(a). The amplitude of β′(t) is about 2°, and its frequency is around 0.1 Hz, which is the same as the natural frequency of the pendulum. The simulation of 500 s physical time without suppression is conducted to get the maximum resonance amplitude of the pendulum. The trajec-tory of the load is plotted in Fig. 12(b), showing that the pendulum amplitude is up to 23 m.

|
| Fig. 12 (a) Excitation roll angle and (b) trajectory of load without suppression |
|
|
A proportional-derivative (PD) control of the cable length is adopted to suppress the pendulation,

|
(36) |
where v(t) is the velocity of the pay-out/reel-in process. The PD parameters are selected so that the length change of the cable is less than 4 m while the best pendulation suppression can be achieved. The results with length control and friction-free (η=1) are shown in Fig. 13, showing that the amplitude of the load is about half of that without control. Moreover, the results with friction of η=0.9 and η=0.8 are shown in Fig. 14, indicating that the friction can significantly suppress the pendulation of the load.

|
| Fig. 13 (a) Pendulation of load with cable control and (b) length change of driving cable (η=1) |
|
|

|
| Fig. 14 Pendulation of load with friction and cable control, (a) η=0.9 and (b) η=0.8 |
|
|
This paper presents an efficient multi-body dynamical approach to model the cable-pulley system with friction. A new ALE cable element is developed, whose length can be changed both actively and passively by introducing an arc-length parameter as one of the nodal generalized coordinates. The cable passing over the pulley is modeled by attaching the pulley to two ALE cable nodes, which naturally forms a moving transitional element. The cable tension decay phenomenon resulting from the cable-pulley friction is derived and modeled as a simple expression of the generalized force acting only on the arc-length coordinate. This method avoids contact detections between the cable and pulley, and the cable can be roughly meshed since the mesh can be dynamically adjusted to adapt to the changing cable configuration, thus significantly saving the computation time. The good accuracy and high efficiency of the proposed method are verified by numerical examples. The presented method of modeling the cable-pulley with friction can be widely used in real engineering applications, and also can be used to model the friction of the sliding joint.
Appendix AAnalytical model of Example 2
As shown in Fig.A1, a planar pendulum with a pulley at the upper end is released from rest and then slides with friction on a cable under the gravity. To get the analytical result, it assumes that the cable mass, the cable elongation and the pulley size are negligible. The centroid of the pendulum is

|
| Fig. A1 Analytical model of Example 2 |
|
|

|
(A1) |
where l is the distance from the sliding point to the center of mass. The linear and angular momentum laws of the pendulum give the following governing equations:

|
(A2) |
where m is the mass of the pendulum, and J is the rotation inertia about the centroid, and

|
(A3) |
The cable-pulley friction results in that the cable tensions at two sides are not equal,

|
(A4) |
From Fig.A1, the following geometrical relationships are obtained:

|
(A5) |
[x θ]T is selected as the generalized coordinate of the system. After substituting Eq.(A4) into Eq.(A2) to eliminate TL and TR and combining the geometrical relations of Eqs.(A3) and (A5), the governing equations are obtained as

|
(A6) |
where

|
(A7) |
| [1] | Yao, R., Tang, X. Q., Wang, J. S., and Huang, P. Dimensional optimization design of the fourcable-driven parallel manipulator in FAST. IEEE/ASME Transactions on Mechatronics, 15, 932-941 (2010) |
| [2] | Riemenschneider, J., Mahrholz, T., Mosch, J., Monner, H. P., and Melcher, J. System response of nanotube based actuators. Mechanics of Advanced Materials and Structures, 14, 57-65 (2007) doi:10.1080/15376490600864620 |
| [3] | You, Z. and Pellegrino, S. Cable-stiffened pantographic deployable structures Ⅱ:mesh reflector. AIAA Journal, 35, 1348-1355 (1997) doi:10.2514/2.243 |
| [4] | Smith, T., Lee, B., Semler, D., and Chae, D. A large S-band antenna for a mobile satellite. Space 2004 Conference and Exhibit, American Institute of Aeronautics and Astronautics, San Diego (2004) |
| [5] | Kimiaghalam, B., Homaifar, A., and Bikdash, M. Pendulation suppression of a shipboard crane using fuzzy controller. American Control Conference, Institute of Electrical and Electronic Engineers, San Diego (1999) |
| [6] | Irvine, H. M. Cable Structures, MIT Press, Cambridge (1981) |
| [7] | Li, Y., Feng, X. Q., Cao, Y. P., and Gao, H. J. A Monte Carlo form-finding method for large scale regular and irregular tensegrity structures. International Journal of Solids and Structures, 47, 1888-1898 (2010) doi:10.1016/j.ijsolstr.2010.03.026 |
| [8] | Zhang, L. Y., Zhao, H. P., and Feng, X. Q. Constructing large-scale tensegrity structures with bar-bar connection using prismatic elementary cells. Archive of Applied Mechanics, 85, 383-394 (2015) doi:10.1007/s00419-014-0958-3 |
| [9] | Zhang, L. Y., Li, Y., Cao, Y. P., and Feng, X. Q. Stiffness matrix based form-finding method of tensegrity structures. Engineering Structures, 58, 36-48 (2014) doi:10.1016/j.engstruct.2013.10.014 |
| [10] | Li, B., Li, Y. H., and Ying, X. G. Dynamic modeling and simulation of flexible cable with large sag. Applied Mathematics and Mechanics (English Edition), 21, 707-714 (2000) doi:10.1007/BF02460190 |
| [11] | Yang, C. J. and Ren, G. X. Dynamic simulation of multifold deployable rings. AIAA Journal, 52, 1555-1559 (2014) doi:10.2514/1.J052187 |
| [12] | Ma, Y. H., He, M. H., Shen, W. H., and Ren, G. X. A planar shock isolation system with highstatic-low-dynamic-stiffness characteristic based on cables. Journal of Sound and Vibration, 358, 267-284 (2015) doi:10.1016/j.jsv.2015.08.011 |
| [13] | Kamman, J. W. and Huston, R. L. Modeling of variable length towed and tethered cable systems. Journal of Guidance, 22, 602-608 (1999) doi:10.2514/2.4423 |
| [14] | Kamman, J. W. and Huston, R. L. Multibody dynamics modeling of variable length cable systems. Multibody System Dynamics, 5, 211-221 (2001) doi:10.1023/A:1011489801339 |
| [15] | Williams, P. and Trivailo, P. Dynamics of circularly towed aerial cable systems Ⅱ:transitional flight and deployment control. Journal of Guidance, 30, 766-779 (2007) doi:10.2514/1.20434 |
| [16] | Williams, P., Lansdorp, B., and Ockels, W. Modeling and control of a kite on a variable length flexible inelastic tether. AIAA Modeling and Simulation Technologies Conference and Exhibit, American Institute of Aeronautics and Astronautics, Hilton Head (2007) |
| [17] | Du, J. L., Cui, C. Z., Bao, H., and Qiu, Y. Y. Dynamic analysis of cable-driven parallel manipulators using a variable length finite element. Journal of Computational and Nonlinear Dynamics, 10, 011013 (2015) |
| [18] | Yu, L., Zhao, Z. H., Tang, J. L., and Ren, G. X. Integration of absolute nodal elements into multibody system. Nonlinear Dynamics, 62, 931-943 (2010) doi:10.1007/s11071-010-9775-6 |
| [19] | Seo, J. H., Sugiyama, H., and Shabana, A. A. Three-dimensional large deformation analysis of the multibody pantograph/catenary systems. Nonlinear Dynamics, 42, 199-215 (2005) doi:10.1007/s11071-005-2789-9 |
| [20] | Sugiyama, H., Escalona, J. L., and Shabana, A. A. Formulation of three-dimensional joint constraints using the absolute nodal coordinates. Nonlinear Dynamics, 31, 167-195 (2003) doi:10.1023/A:1022082826627 |
| [21] | Lee, S. H., Park, T. W., Seo, J. H., Yoon, J. W., and Jun, K. J. The development of a sliding joint for very flexible multibody dynamics using absolute nodal coordinate formulation. Multibody System Dynamics, 20, 223-237 (2008) doi:10.1007/s11044-008-9109-3 |
| [22] | Belytschko, T., Liu, W. K., Moran, B., and Elkhodary, K. I. Nonlinear Finite Elements for Continua and Structures, 2nd ed , John Wiley and Sons, Chichester (2014) |
| [23] | Hong, D. F. and Ren, G. X. A modeling of sliding joint on one-dimensional flexible medium. Multibody System Dynamics, 26, 91-106 (2011) doi:10.1007/s11044-010-9242-7 |
| [24] | Hong, D. F., Tang, J. L., and Ren, G. X. Dynamic modeling of mass-flowing linear medium with large amplitude displacement and rotation. Journal of Fluids and Structures, 27, 1137-1148 (2011) doi:10.1016/j.jfluidstructs.2011.06.006 |
| [25] | Ma, Y. H., Hong, D. F., Cheng, Z. B., Cao, Y. F., and Ren, G. X. A multibody dynamic model of the drilling system with drilling fluid. Advances in Mechanical Engineering, 8, 1-16 (2016) |
| [26] | Ferdinand, P., Beer, E., Russell, J., and David, F. M. Vector Mechanics for Engineers:Statics, 10th ed , McGraw-Hill, New York, 449-451 (2013) |
| [27] | Hu, Z. D. and Hong, J. Z. Modeling and analysis of a coupled rigid-flexible system. Applied Mathematics and Mechanics (English Edition), 20, 1167-1174 (1999) doi:10.1007/BF02460335 |
| [28] | Hairer, E. and Wanner, G. Solving Ordinary Differential Equations Ⅱ:Stiff and Differential-Algebraic Problems, 2nd ed , Springer, Berlin (2010) |
| [29] | Petzold, L. and Lötstedt, P. Numerical solution of nonlinear differential equations with algebraic constraints Ⅱ:practical implications. SIAM Journal on Scientific and Statistical Computing, 7, 720-733 (1986) doi:10.1137/0907049 |
| [30] | Cao, D. Z., Qiang, H. F., and Ren, G. X. Parallel computing studies of flexible multibody system dynamics using OpenMP and Pardiso (in Chinese). Journal of Tsinghua University (Science and Technology), 52, 1643-1649 (2012) |
 2017, Vol. 38
2017, Vol. 38




