Shanghai University
Article Information
- ZHAO, Y. P., CAO, W.
- Calculation of thermal physical parameters of dissociated air by the dissociation degree method
- Applied Mathematics and Mechanics (English Edition), 2018, 39(7): 1045-1056.
- http://dx.doi.org/10.1007/s10483-018-2348-8
Article History
- Received Oct. 16, 2017
- Revised Feb. 10, 2018
For designing hypersonic aircrafts flying at a high altitude, whether transition will happen or not and transition position prediction are important issues. Due to the high temperature, the thermodynamic properties of gas vary greatly in hypersonic flows. This makes accurate calculation of aerodynamic heating and resistance more difficult. Therefore, it is essential to determine the thermodynamic properties of gas[1]. The specific heat of air is assumed to be a constant value in the computation of the location prediction of transition and turbulence of supersonic flows when the Mach number is not very large and the gas temperature is not significant[2]. When the air temperature range is from 600 K to 2 500 K, the molecular vibration degrees of freedom of O2 and N2 molecules in the air are excited, and the specific internal energy can be expressed as a function of the temperature[3]. The specific heat of air is also a function of the temperature. Mao and Cao[4] studied the prediction of hypersonic boundary layer transition on sharp wedge flows considering variable specific heat. For the above two cases, the equations of state for a perfect gas are still satisfied. As the aircraft flies at hypersonic speeds, such as the Mach number greater than 8, the air temperature will increase due to shock waves or near the solid wall inside the boundary layer. When the temperature reaches 2 000 K and 4 000 K, O2 and N2 molecules are successively dissociated, respectively. Then, the air is a mixture of molecules and atoms. The proportion of each component and thermal physical parameters would vary with different pressures and temperatures. And it no longer satisfies the equation of state of a perfect gas. How to accurately calculate thermal physical parameters of dissociated air is worth studying.
According to thermochemical equilibrium conditions, a series of studies have been done on the calculation of thermal physical parameters of dissociated air. In 1958, in the temperature range from 500 K to 15 000 K, Hansen[5] assumed that chemical reactions can be treated independently for the purposes of approximation. Then, the calculation of thermal physical parameters can be divided into three cases. The equilibrium constant is used to establish the relationship between the variable Θµ and pressure. And then thermal physical parameters are obtained. In 2014, Fan and Lou[6] used the equilibrium constant method to calculate thermal physical parameters for a seven-component model. Zhu et al.[7] used the piecewise curve fitting method to study thermal physical parameters of the equilibrium air. The density and pressure of thermal physical parameters are served as independent variables. The acoustic velocity, enthalpy, average molecular weight, and temperature of the equilibrium air are approximately calculated by fitting formulas, respectively. Yu and McBride[8] and Liu and Vinokur[9] have used the minimum free energy method to study thermal physical parameters in an equilibrium state. The equilibrium constant method is used to calculate the equilibrium constant first. Its solution process is cumbersome and complex. The empirical curve fitting method could not provide an accurate value for any pressure and temperature. The minimum free energy method requires the use of thermodynamic variables as a function of the temperature. It is worthwhile to study the thermal physical parameters of dissociated air with a simple and convenient method.
Equations among the dissociation degree, temperature, and pressure are established. Then, the relationships between the dissociation degree and thermal physical parameters of the dissociated air are also set up. Thus, the parameters can be calculated by solving the dissociation degree. The method is used to study thermodynamic properties of the dissociated air containing four species, that is, O2 and N2 molecules, O and N atoms, and the results are compared with those using the traditional equilibrium constant method.
2 Calculation of thermal physical parameters by the dissociation degree method 2.1 Dissociation degree of O2 and N2 molecules in airThe dissociated reaction of O2 and N2 molecules can be expressed as the following formula:
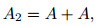
|
(1) |
where A2 and A represent one molecule and one atom, respectively. According to Ref. [10], α, the dissociation degree, is defined as below,
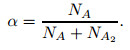
|
(2) |
The value of α ranges from zero to one, where zero and one stand for no dissociation and complete dissociation, respectively. According to Ref. [10], in a thermochemical equilibrium state, the relation between the number of particles and the partition function is
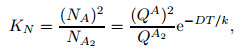
|
(3) |
where QA and QA2 are atomic and molecular partition functions, respectively, and T stands for the temperature. D is the dissociation energy of one molecule A2 and also called the heat reaction of one molecule A2. As the temperature is greater than the vibrational characteristic temperature of molecules, the vibrational energy of the molecules will be excited completely. If the distance between molecules increases, the molecular potential energy tends to be a constant value called the dissociation energy of molecules. That is, the energy required for the dissociation of molecules is D. D/k is the dissociation characteristic temperature of A2 molecules. The dissociation characteristic temperatures of O2 and N2 molecules are 59 000 K and 113 200 K, respectively.
The density of gas mixtures including A2 molecules and A atoms is
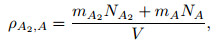
|
(4) |
where mA and mA2 are the masses of one atom and one molecule, respectively, and V represents the volume of gas mixture. NA and NA2 are obtained with the simultaneous equations (2) and (4). Then, NA and NA2 are input into Eq. (3) to get the following formula:
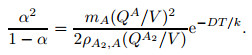
|
(5) |
Atomic and molecular partition functions are substituted into Eq. (5), i.e.,
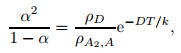
|
(6) |
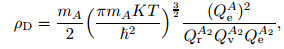
|
(7) |
where ρD is called the dissociated characteristic density, which is a function of temperature.
The volume of gas mixtures in Eq. (6) keeps unchanged. Therefore, the relationship between the density of gas mixtures and the air density is
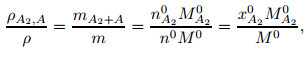
|
(8) |
where xA20 is the molar fraction of A2 molecules under the normal temperature and pressure, M0 is the molar mass (M0=0.028 84 kg/mol), and the superscript "0" stands for the parameter value at the normal temperature and pressure. The following relation can be obtained by combining Eqs. (6) and (8):
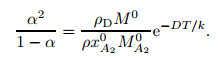
|
(9) |
Only the dissociation of O2 molecules and N2 molecules is taken into consideration. Then, the dissociation reactions are
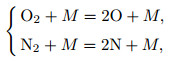
|
(10) |
where M is a colliding particle that can be any atom or molecule.
There are four kinds of components for the dissociated air, namely, O2 molecules, N2 molecules, O atoms, and N atoms. For the thermochemical equilibrium procedure, the mole fractions of each component are as follows:
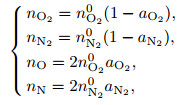
|
(11) |
where aO2 and aN2 are the dissociation degrees of O2 molecules and N2 molecules, respectively, and n0 is the initial mole number of the corresponding molecules. According to the aerodynamics[3], the compressibility factor is
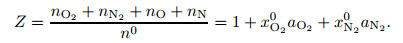
|
(12) |
The greater the compressibility factor becomes, the more the gas mixtures deviate from the perfect gas. At the normal temperature and pressure, components of air are approximately N2 (79%), O2 (20%), and trace elements (1%), such as Ar, He, CO2, and H2O. In the case of neglecting the trace elements, the air is composed of N2 (79%) and O2 (21%). Considering the unit mole gas, xO20 and xN20 are 0.21 and 0.79, respectively.
The equation of state for the dissociated air is expressed as
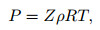
|
(13) |
where R is the gas constant, whose value is equal to R0/M0. R0 is the universal gas constant (R0=8.314 J/(mol·K)), and M0 is the molar mass (M0=0.028 84 kg/mol).
Equations (12) and (13) are substituted into Eq. (9), and then the dissociation degree satisfies the following equations:
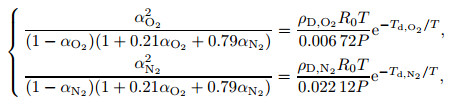
|
(14) |
where P represents the pressure of the gas mixture. The dissociation degrees are functions of pressure and temperature. The dissociation degrees of O2 molecules and N2 molecules can be solved by using the Newton iterative method.
The mole fractions of each component for the dissociated air are as follows:
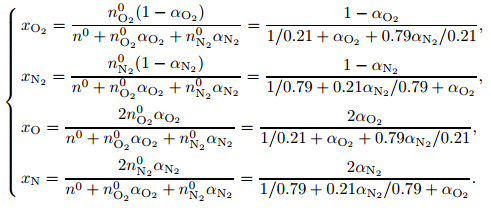
|
(15) |
The average molecular weight of the gas mixtures can be written as
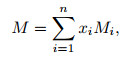
|
(16) |
where Mi is the molecular weight of the ith-component, and n represents the number of air components.
2.3 Relationship among internal energy and enthalpy and dissociation degreeThe internal energy of the air is given by the following formula:
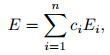
|
(17) |
where ci is the mass fraction. According to statistical mechanics, for a single gas, the internal energy can be divided into four parts, the translational energy, the rotational energy, the vibrational energy, and the electron excitation energy,
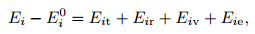
|
(18) |
where Ei0 is the zero point energy of the ith-component and is also equal to the zero point enthalpy hi0. The zero point enthalpy per unit mass in the present paper, which is derived from Refs. [11] and [12], is listed in Table 1.
For monatomic gases, the internal energy consists of the translational and electron excitations. The internal energies per unit mass of each element are
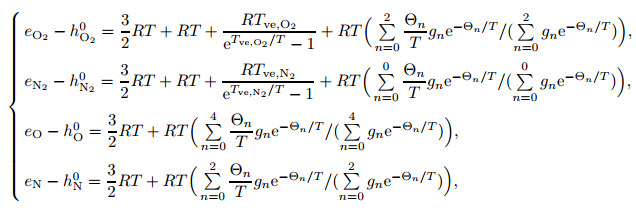
|
(19) |
where Tve, O2 and Tve, N2 are the vibrational characteristic temperatures of O2 molecules and N2 molecules, respectively. The vibrational characteristic temperatures of O2 and N2 molecules are 2 270 K and 3 390 K, respectively. R is the gas constant of the gas mixtures, Θn is the electronic characteristic temperature, and gn is the electronic degree of degeneracy. The characteristic temperature is the property of the molecule, which is only related to the molecule itself.
The relationship between the mass fraction of each component and the mole fraction can be expressed as
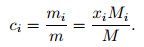
|
(20) |
According to the mass fraction and internal energy per unit mass of each component, the total internal energy of gas mixtures can be obtained.
The enthalpy is obtained according to the follow relationship:
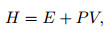
|
(21) |
where H and E stand for the total enthalpy and total internal energy, respectively.
2.4 Relationship between heat capacity and compressibility factorAccording to the definition of heat capacity at the constant pressure,
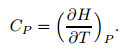
|
(22) |
According to the definition of heat capacity at the constant volume,
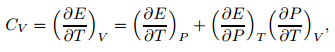
|
(23) |
where 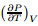
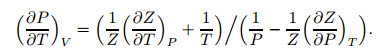
|
(24) |
According to the acoustic velocity definition,
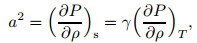
|
(25) |
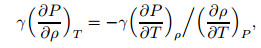
|
(26) |
where γ is the specific heat ratio. Combine the equation of state to get the acoustic velocity, and the following equation can be obtained:
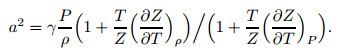
|
(27) |
The relationship between the partial pressure of each component and the total pressure is
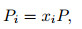
|
(28) |
where Pi is the partial pressure of the ith-component. Thus, the problem of solving the mole fraction xi for each component is transformed into solving the partial pressure problem for each component. For the given temperature T and pressure P, according to the law of Dalton's partial pressure, the total pressure of gas mixtures is the sum of all partial pressures,
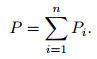
|
(29) |
According to the equilibrium conditions of the dissociation of O2 molecules and N2 molecules,
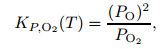
|
(30) |
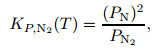
|
(31) |
where KP, i(T) is a function of temperature, and i is the component of gas mixture.
According to the principle of conservation of mass, the ratio of the total number of O atoms to the total number of N atoms is unchanged,
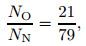
|
(32) |
where N is the number of particles. The ratio of the number of particles in Eq. (31) can be converted to the partial pressure ratio of the component by the equation of state, that is, NO/NN=(2PO2+P O)/(2PN2+PN).
According to Refs. [5] and [13], the equilibrium constant is calculated as
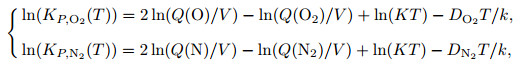
|
(33) |
where the partition functions of each component are obtained as
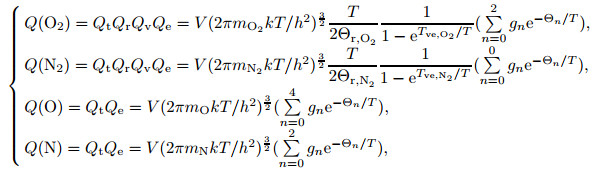
|
(34) |
where Θr, O2 and Θr, N2 are the rotational characteristic temperatures of O2 molecules and N2 molecules, respectively. The rotational characteristic temperatures of O2 and N2 molecules are 2.1 K and 2.9 K, respectively. By solving the partial pressure equations of each component in the equilibrium air, the partial pressure of each component is obtained, and then the mole fraction xi of each component is obtained.
The average molecular weight of the gas mixtures can be written as
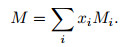
|
(35) |
According to aerodynamics[3], the compressibility factor Z can be expressed as
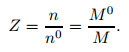
|
(36) |
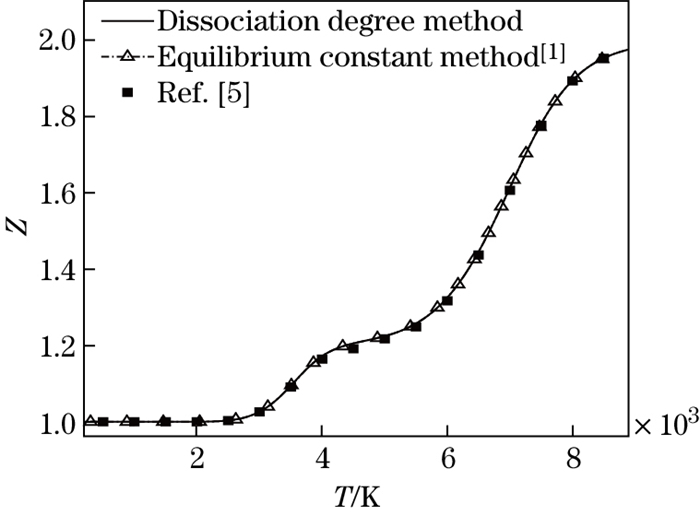
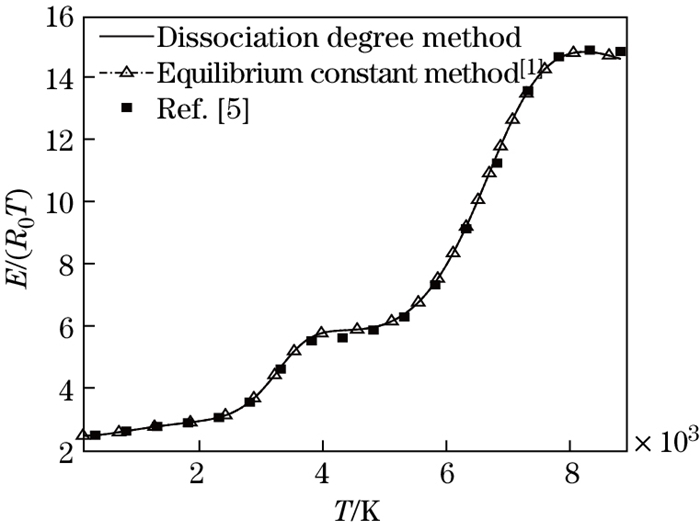
Other thermal physical parameters can be obtained by the above relations. In order to examine whether the new method is correct or not, the comparisons of the compressibility factor and the dimensionless enthalpy calculated with the three methods, the new method, the traditional one in Ref. [1], and the method proposed by Hansen[5], are shown in Figs. 1 and 2. It can be seen from Figs. 1 and 2 that the results agree well with each other. It is shown that the dissociation degree method is reliable in the calculation of thermal physical parameters of the dissociated air.
|
| Fig. 1 Comparison of compressibility factor |
|
|
|
| Fig. 2 Comparison of dimensionless internal energy |
|
|
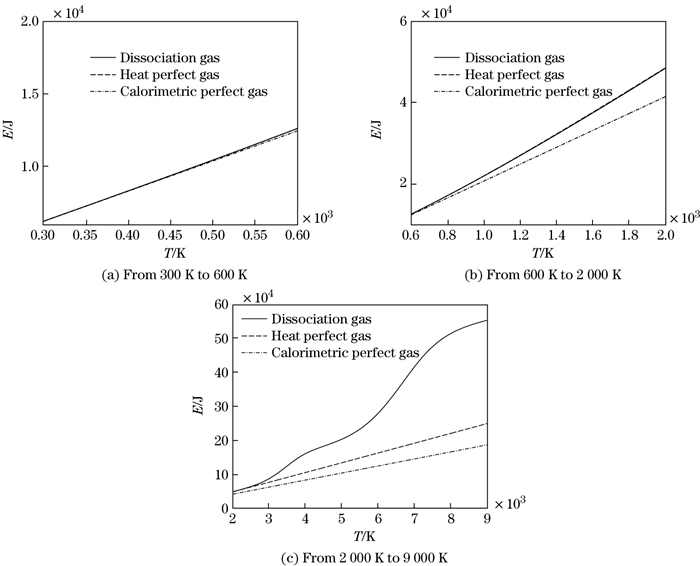
At the standard atmospheric pressure and the temperature range from 300 K to 9 000 K, thermal physical parameters, such as the internal energy, the enthalpy, the heat capacity, and the specific heat ratio, are calculated with the dissociation degree method.
The internal energy is calculated with the three models, the calorimetric perfect gas, the heat perfect gas, and the dissociated gas. The comparisons of the results calculated with the three kinds of models in different temperature ranges, [300 K, 600 K], [600 K, 2000 K], and [2 000 K, 9 000 K], respectively, are shown in Figs. 3(a), 3(b), and 3(c). It can be seen from Fig. 3(a) that the three curves coincide, which means that all models satisfy the calorimetric perfect gas property in the temperature range from 300 K to 600 K. That is, the specific heat is a constant, independent of temperature. It can be seen from Fig. 3(b) that the curve of the calorimetric perfect gas is apart from the other two modes. It is illustrated that the air does not dissociate, and only the vibration energy is excited. Moreover, the specific heat is related to the temperature and is no longer a constant. When the temperature lies between 2 000 K and 9 000 K, O2 and N2 molecules in the air start to dissociate sequentially. With the increase in the temperature, the degree of deviation among three curves becomes larger as shown in Fig. 3(c). Thus, the effect of molecular dissociation on thermal physical parameters is great.
|
| Fig. 3 Comparisons of internal energy calculated with three kinds of models in different temperature ranges |
|
|
The dissociation degrees of O2 and N2 molecules versus the temperature are shown in Fig. 4. It can be seen that O2 molecules begin to dissociate at 2 000 K. When the temperature reaches 4 000 K, about 80 percent of O2 molecules dissociate, and N2 molecules begin to dissociate. When the temperature reaches 9 000 K, N2 molecules dissociate almost completely. The compressibility factor versus the temperature is shown in Fig. 5. It can be seen that the compressibility factor increases when the temperature increases. The compressibility factor is 1, 1.21, and 2, with temperature being less than 2 000 K, about 4 500 K, and equal to 9 000 K, respectively.
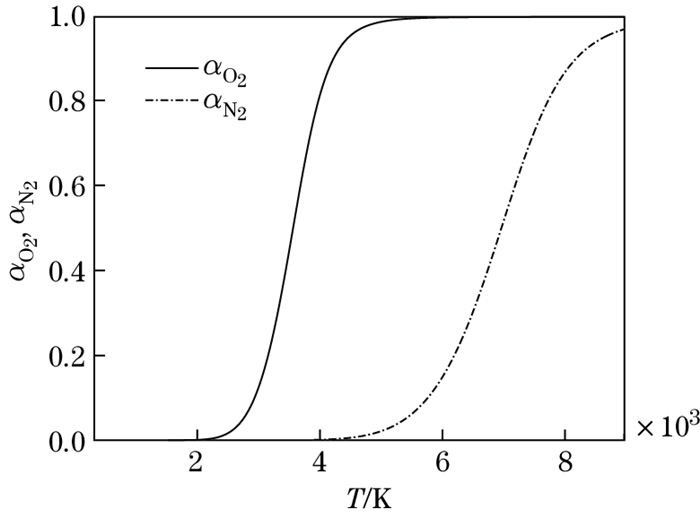
|
| Fig. 4 Dissociation degree versus temperature |
|
|
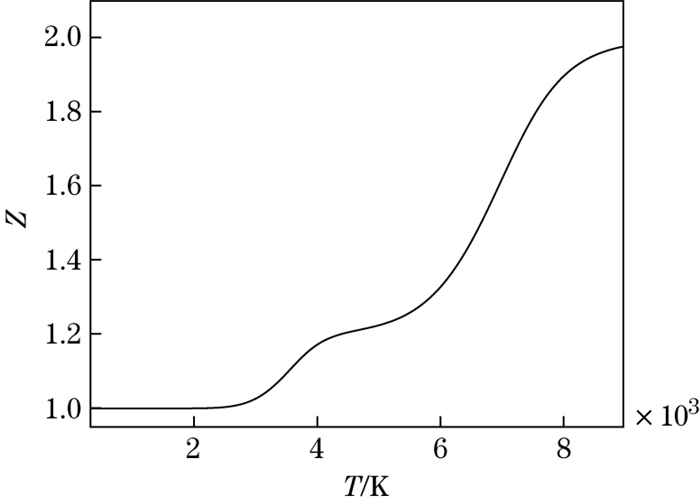
|
| Fig. 5 Compressibility factor versus temperature |
|
|
The dimensionless internal energy versus the temperature is shown in Fig. 6. It can be seen that in the temperature range from 2 000 K to 4 500 K and from 4 000 K to 9 000 K, corresponding to the O2 and N2 molecule dissociation, the slope of the curve will increase with the increase in the temperature. The molecular dissociation is endothermic. The ratio of specific heat to the temperature is shown in Fig. 7. It can be seen that the value of the ratio of specific heat is less than 1.4 for the dissociated air.
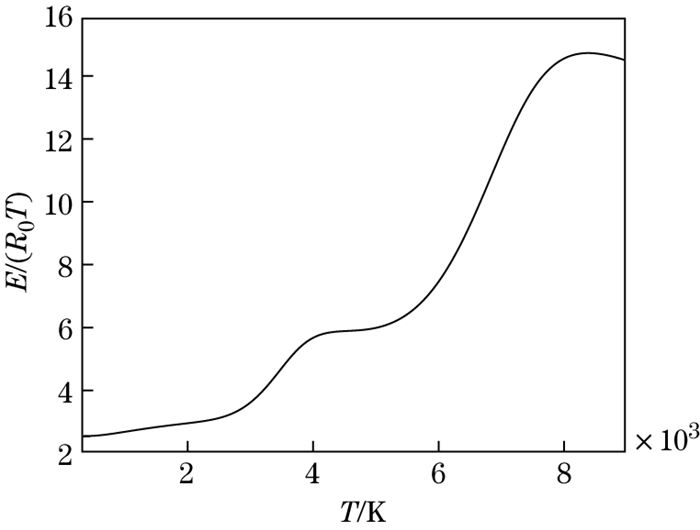
|
| Fig. 6 Dimensionless internal energy versus temperature |
|
|
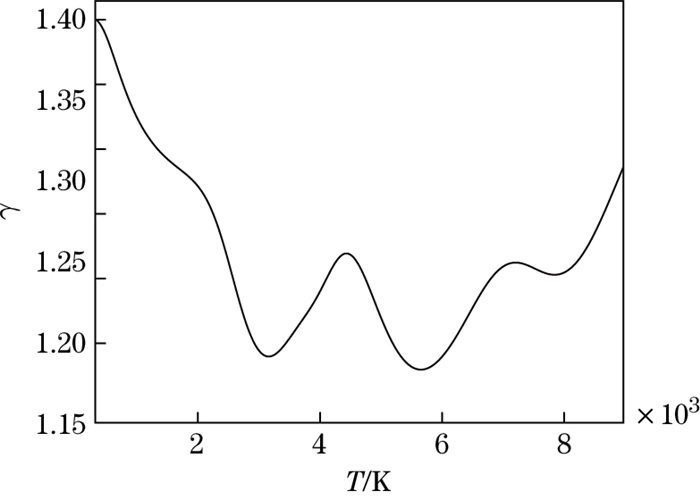
|
| Fig. 7 Ratio of specific heat versus temperature |
|
|
In order to study how the pressure affects the value of the thermal physical parameters, the results at three different pressures are given as follows.
The dissociation degree of O2 molecules versus the temperature at different pressures is shown in Fig. 8. It can be seen that, for the same temperature, the higher the pressure is, the lower the dissociation degree is. The reason is that, the higher the pressure is, the stronger the molecular binding ability is, and the more difficult the dissociation is. The compressibility factor versus the temperature at different pressures is shown in Fig. 9. It can be seen that, for the same temperature, the greater the pressure is, the smaller the compressibility factor and the deviation from the perfect gas are.
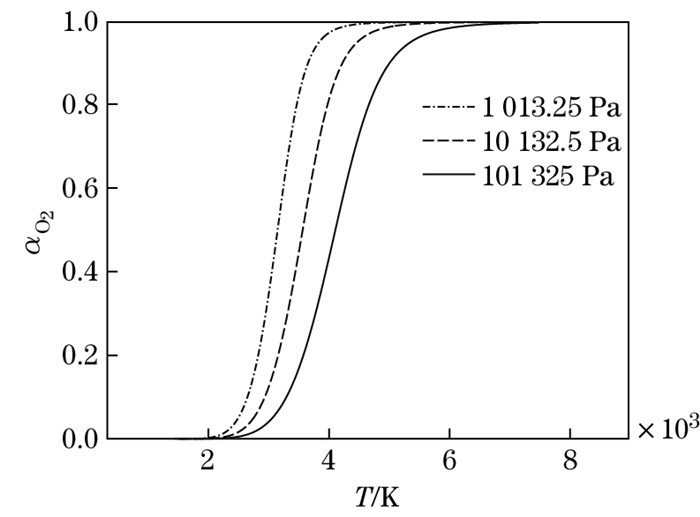
|
| Fig. 8 Dissociation degree versus temperature at different pressures |
|
|
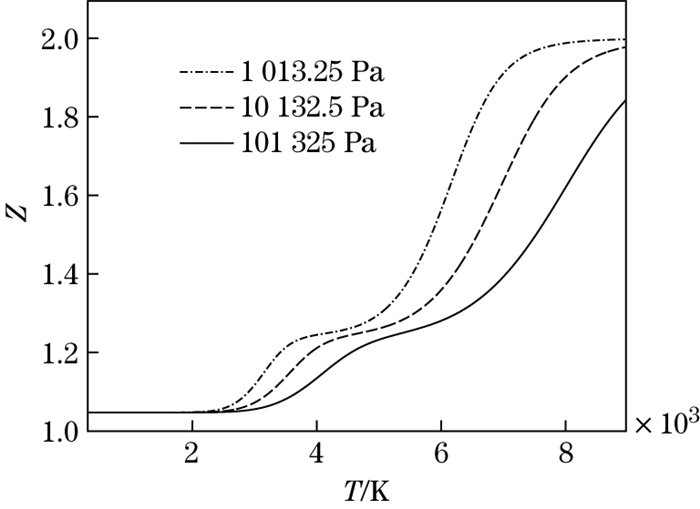
|
| Fig. 9 Compression factor versus temperature at different pressures |
|
|
The dimensionless internal energy versus the temperature at different pressures is shown in Fig. 10. It can be seen that, for the same temperature, the larger the pressure is, the smaller the dimensionless internal energy and the slope of the curve are. The ratio of specific heat versus the temperature at different pressures is shown in Fig. 11. It can be seen that, for the same temperature, when the pressure is higher, the ratio of specific heat is closer to the perfect gas value. It is shown that molecular dissociation easily occurs at the low pressure.
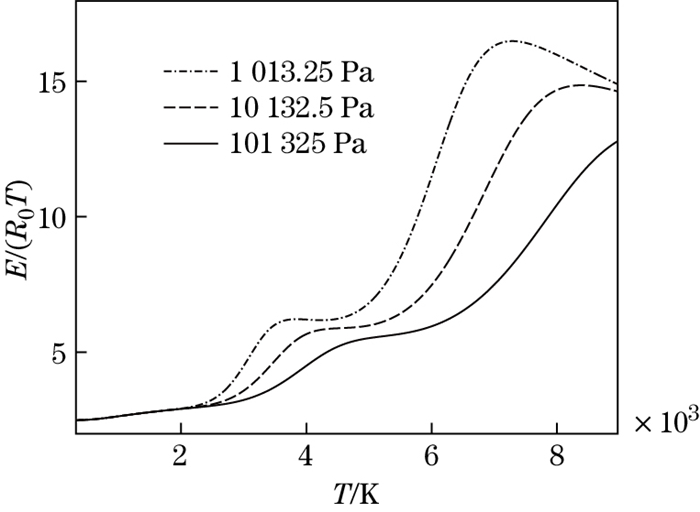
|
| Fig. 10 Dimensionless internal energy versus temperature at different pressures |
|
|
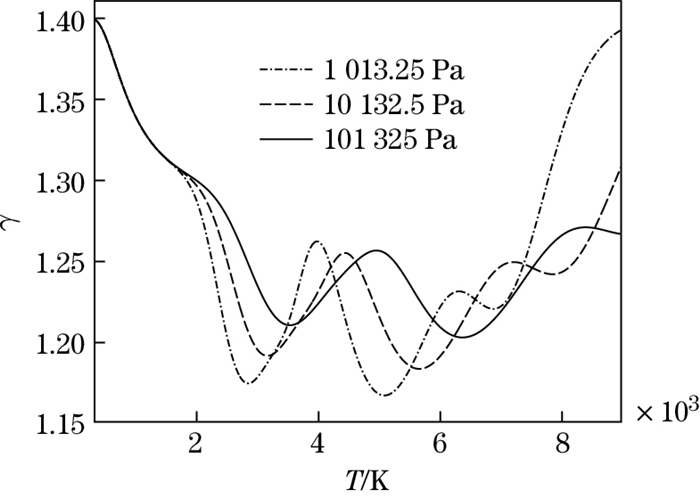
|
| Fig. 11 Ratio of specific heat versus temperature at different pressures |
|
|
(Ⅰ) The thermal physical parameters of dissociated air whose components vary with the temperature can be calculated with the dissociation degree method. Compared with the traditional equilibrium constant method, the new one is of much more intuitive understanding.
(Ⅱ) Unlike the perfect gas, all the thermal physical parameters of the dissociated air are functions of the temperature and pressure. If the pressure keeps constant, the dissociation degree of O2 or N2 and the compressibility factor will become large as the temperature increases. The curve of internal energy versus the temperature has two peaks which correspond to the dissociation reactions of O2 and N2 molecules, respectively. If the temperature keeps constant, the lower the pressure is, the larger the dissociation degree and the compressibility factor are. The dissociation reaction should be considered for the high temperature or low pressure.
It is worth mentioning that the dissociation degree method proposed in this paper has good effects on the coexistence of the dissociation and the compound process. However, for more complex chemical reactions, such as the existence of combination reactions, whether it is suitable and how to popularize the dissociation method are still under further study.
| [1] | LIANG, D. W., LI, B., and RONG, W. Thermodynamic characteristics of thermally perfect gas and solution of N-S equations. Journal of Nanjing University of Aeronautics & Astronautics, 35(4), 424-429 (2003) |
| [2] | CAO, W. and ZHOU, H. Numerical investigation of evolution of disturbances in two-dimensional hypersonic boundary layer and the influence of the presence of shocklets on the structure of flow. Science in China Series G, 34(2), 203-212 (2004) |
| [3] | TONG, B. G., KONG, X. Y., and DENG, G. H Aerodynamics, Higher Education Press, Beijing (1990) |
| [4] | MAO, X. and CAO, W. Prediction of hypersonic boundary layer transition on sharp wedge flow considering variable specific heat. Applied Mathematics and Mechanics (English Edition), 35(2), 143-154 (2014) doi:10.1007/s10483-014-1779-7 |
| [5] | HANSEN, C. F. Approximations for the Thermodynamic and Transfer Properties of HighTemperature Air, National Advisory Committee for Aeronautics, U. S. A (1958) |
| [6] | FAN, Y. and LOU, J. S. Flow stability and transition prediction of an equilibrium air model. Journal of Aerospace Power, 31(8), 1658-1668 (2016) |
| [7] | ZHU, Y. L., ZHONG, X. C., CHEN, B. M., and ZHANG, Z. M Initial Boundary Value Problems, Difference Methods, and Disturbed Flows, Science Press, Beijing (1980) |
| [8] | YU, S. T. and MCBRIDE, B. J. Numerical simulation of hypersonic inlet flows with equilibrium or finite rate chemistry. 26th Aerospace Sciences Meeting, American Institute of Aeronautics and Astronautics, Reno (1988) |
| [9] | LIU, Y. and VINOKUR, M. Equilibrium gas flow computations Ⅰ :accurate and efficient calculation of equilibrium gas properties. 24th Thermophysics Conference, American Institute of Aeronautics and Astronautics, New York (1989) |
| [10] | BIAN, Y. G. and ZHONG, J. K High Temperature Boundary Layer Heat Transfer, Science Press, Beijing (1986) |
| [11] | MCBRIDE, B. J., HEIMEL, S., EHLERS, J. G., and GORDON, S. Thermodynamic Properties to 6000 K for 210 Substances Involving the First 18 Elements, National Aeronautics and Space Administratio, Washington D. C (1963) |
| [12] | WU, Z. N Aerodynamics, Tsinghua University Pres, Beijing (2007) |
| [13] | PALMER, G. E. An implicit flux-split algorithm to calculate hypersonic flow fields in chemical equilibrium. 22nd Thermophysics Conference, American Institute of Aeronautics and Astronautics, Honolulu (1987) |
 2018, Vol. 39
2018, Vol. 39



