Shanghai University
Article Information
- Lianhe LI, Guanting LIU
- Study on a straight dislocation in an icosahedral quasicrystal with piezoelectric effects
- Applied Mathematics and Mechanics (English Edition), 2018, 39(9): 1259-1266.
- http://dx.doi.org/10.1007/s10483-018-2363-9
Article History
- Received Jan. 4, 2018
- Revised Mar. 7, 2018
2. Inner Mongolia Key Laboratory of Nanoscience and Nanotechnology, Inner Mongolia University, Huhhot 010021, China
The unique structure and physical-mechanical characteristics of quasicrystals open the way to technological applications in many fields[1]. The icosahedral quasicrystal is one of the most widely used quasicrystal materials, with a good development future[2-3].
Mechanical properties and fracture behavior of quasicrystals have recently attracted considerable interest[4-5]. The generalized Dugdale model of quasicrystals has been considered with the help of conformal mapping method[6]. Li et al.[7] investigated the buckling and the free vibration of properties of a two-dimensional hexagonal cylindrical shell under axial compression. Collinear periodic crack problems were considered in Ref. [8]. The influence of phason displacement on the related physical quantities was discussed. Fourier images of Green's functions for dynamic plane elasticity problems of decagonal quasicrystals were obtained by using the Fourier transform and matrix transformation method[9]. The plate bending analysis in one-dimensional orthorhombic quasicrystals under static and transient dynamic loads was studied by the meshless Petrov-Galerkin method[10]. Using an extended technique of continuous dislocation layers, a moving antiplane shear strip crack problem in one-dimensional hexagonal was investigated[11].
The coupling behavior between elastic and electric fields of piezoelectric materials brings good prospects in electro-mechanical and electronic devices. Piezoelectricity is an important physical property of quasicrystals[12]. However, the knowledge and understanding of the piezoelectric behavior of quasicrystals are still limited, especially for two- and three-dimensional quasicrystals. The piezoelectricity tensor associated with the phonon fields was obtained by Rama et al.[13]. The piezoelasticity of quasicrystals induced by both phonon and phason fields was discussed in Ref. [14]. Three-dimensional fundamental solutions of one-dimensional quasicrystals with the piezoelectric effect were obtained in Refs. [15] and [16]. The general solutions to the piezoelasticity problem for one-dimensional quasicrystals with all point groups were derived based on the operator method and the complex variable function method by Yu et al.[17]. Then, an antiplane elliptical cavity of one-dimensional hexagonal piezoelectric quasicrystals was investigated[18]. A circular hole with a straight crack in one-dimensional hexagonal quasicrystals with piezoelectric effects was considered by Yang and Li[19].
The electrical and elastic fields induced by the dislocation in an icosahedral quasicrystal with piezoelectric effects are derived using the extended Stroh formalism in this paper. Numerical analysis is then conducted to discuss the influence of piezoelectric constants on the displacements and the electric potential.
2 Stroh formalism for two-dimensional deformation of icosahedral quasicrystals with piezoelectric effectsAccording to the elastic theory of piezoelectric quasicrystals[14], we have the gradient equations

|
(1) |
the equilibrium equations (if the body force is neglected)
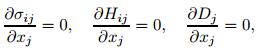
|
(2) |
and the linear electric-elastic coupled constitutive equations

|
(3) |
in which Cijkl and Kijkl are elastic constants of the phonon and phason fields, respectively, Rijkl are the phonon-phason coupling elastic constants, Di, ϕ, and Ei are the electric displacements, electric potential, and electric fields, respectively, χij is the dielectric permittivity, and eijk and dijk are piezoelectric constants of the phonon and phason fields, respectively.
Assume that the defect is parallel to the fivefold direction of icosahedral quasicrystals[20]. Making use of Eqs. (1)-(3), we obtain

|
(4) |
Let
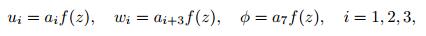
|
(5) |
in which
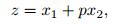
|
f(z) is an arbitrary function of z, and p and ai are the unknown complex constants to be determined. Substituting Eq. (5) into Eq. (4), we have
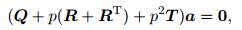
|
(6) |
where
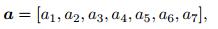
|
and the 7× 7 matrices Q, R, and T are given by
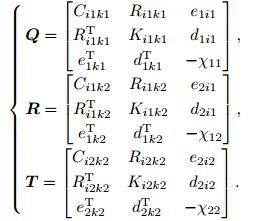
|
(7) |
A nontrivial solution for a exists if the determinant of the matrix in Eq. (6) is zero, i.e.,

|
(8) |
The associated eigenvector a can be obtained from Eq. (6). Then, the general solutions can be expressed as

|
(9) |
where
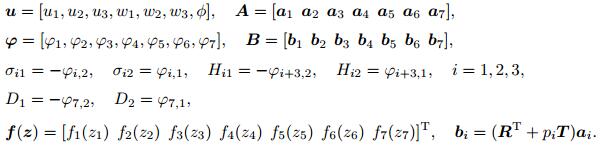
|
Without loss of generality, let Im pα >0.
3 Coupled fields caused by line dislocationThe fundamental properties of dislocations in quasicrystals were discussed in Refs. [21] and [22]. The results of the discussion show that the characteristic vector b*, i.e., the Burgers vector of a dislocation, is a direct sum
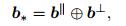
|
where b|| and b⊥ describe rigid translations in the physical and complementary subspaces, respectively. The elastic displacement fields induced by a dislocation consist of u and w, i.e., the phonon and phason displacement fields, due to the presence of incommensurate length scales in quasicrystals.
The dislocation is assumed to be infinitely long in the fivefold direction, the core at the origin. Without loss of generality, we take the plane x2 = 0 and x1 < 0 to be the slip plane. Introducing a branch cut along the negative x1-axis, we have r > 0 and -π < θ < π (where x1 = r cosθ and x2 = r sinθ).
The boundary conditions of this problem can be expressed as

|
(10) |
in which 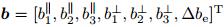
Let

|
(11) |
where qα are arbitrary complex constants. Equation (9) can then be written as

|
(12) |
in which 〈ln zα〉 is the diagonal matrix,

|
(13) |
Substituting Eq. (12) into Eq. (10) yields

|
(14) |
The dielectric constants and piezoelectric constants of phonon and phason fields have not yet been measured for the icosahedral Al-Pd-Mn. The numerical results are presented to show the effects of the phonon piezoelectric constant e14 and the phason piezoelectric constant d123 on the displacements and the electric potential. The material properties[23] are given by
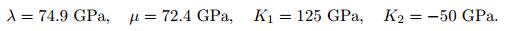
|
In the computation, we assume that the phason piezoelectric constant d132=13 C· m-2 and the dielectric constant χ11=60×10-10 C· (V·m)-1. Other parameters are taken to have the values below
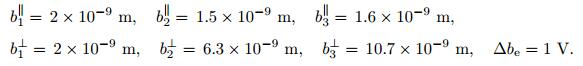
|
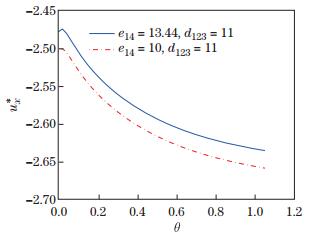
The normalized displacements ux* and wx* (i.e., ux*=ux/10-10 m and wx*=wx/10-10 m) and the electric potential ϕ versus the angular θ under different piezoelectric constants of phonon and phason fields are depicted in Figs. 1-6, where r is fixed at r=15× 10-9 m. The coupling constant R of the quasicrystal has not yet been measured. In the computation, we assume that R=951 MPa.
|
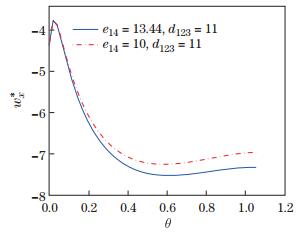
| Fig. 1 Variation of the normalized displacements ux* versus θ for different e14 |
|
|
|
| Fig. 2 Variation of the normalized displacements wx* versus θ for different e14 |
|
|
|
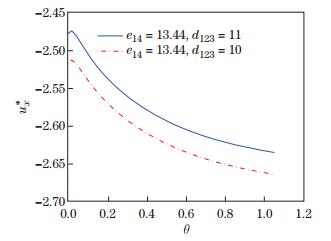
| Fig. 3 Variation of the normalized displacements ux* versus θ for different d123 |
|
|

|
| Fig. 4 Variation of the normalized displacements wx* versus θ for different d123 |
|
|

|
| Fig. 5 Variation of the electric potential ϕ versus θ for different e14 |
|
|
|
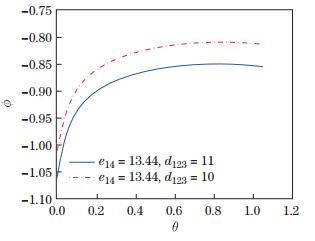
| Fig. 6 Variation of the electric potential ϕ versus θ for different d123 |
|
|
The figures show that the phonon displacements, phason displacements, and the electric potential are significantly affected by the piezoelectric constants. With the variation of the phonon piezoelectric constant (see Figs. 1 and 2), a different changing tendency of the phonon displacement ux and phason displacement wx is observed. From Figs. 3 and 4, we draw the conclusion that the displacements ux and wx have the same tendency with the variation of the phason piezoelectric constants, but different in the extent. Figures 5 and 6 show that the phason piezoelectric constant has more influence on the electric potential than the phonon piezoelectric constant.
The effects of the phonon-phason coupling elastic constant R on the normalized displacements ux* and wx* are discussed in Figs. 7 and 8. As the value of R increases, the absolute values of the normalized displacements ux* and wx* decrease.

|
| Fig. 7 The effects of coupling elastic constant R on the normalized displacements ux* |
|
|

|
| Fig. 8 The effects of coupling elastic constant R on the normalized displacements wx* |
|
|
A theoretical and numerical treatment of a line dislocation in icosahedral quasicrystals with piezoelectric effects is presented by using the extended Stroh formalism. The effects of the piezoelectric constants on the displacements and the electric potential are discussed. The results are reduced to the classical ones when the electric field is neglected. These results are valuable for understanding the effects of dislocations on icosahedral quasicrystals with piezoelectric effects.
| [1] | SUCK, J. B., SCHREIBER, M., and HAUSSLER, P. Quasicrystals:an introduction to structure.Physical Properties and Applications, Springer, Berlin (2002) |
| [2] | FAN, T. Y. Mathematical Theory of Elasticity of Quasicrystals and Its Applications, Springer, Beijing (2011) |
| [3] | ATHANASIOU, N. S., POLITIS, C., SPIRLET, J. C., BASKOUTAS, S., and KAPAKLIS, V. The significance of valence electron concentration on the formation mechanism of some ternary aluminum based quasicrystals. International Journal of Modern Physics B, 16, 4665-4683 (2002) doi:10.1142/S0217979202013067 |
| [4] | FAN, T. Y. and MAI, Y. W. Elasticity theory, fracture mechanics and some thermal properties of quasicrystalline materials. Applied Mechanics Reviews, 57(5), 325-344 (2004) doi:10.1115/1.1763591 |
| [5] | LI, X. F. and FAN, T. Y. New method for solving elasticity problems of some planar quasicrystals and solutions. Chinese Physics Letter, 15, 278-280 (1998) doi:10.1088/0256-307X/15/4/016 |
| [6] | LI, W. and FAN, T. Y. Exact solutions of the generalized Dugdale model of two-dimensional decagonal quasicrystals. Applied Mathematics and Computation, 218(7), 3068-3071 (2011) doi:10.1016/j.amc.2011.08.025 |
| [7] | LI, Y. S., FENG, W. J., and ZHANG, C. Buckling and vibration of the two-dimensional quasicrystal cylindrical shells under axial compression. Applied Mathematical Modelling, 50, 68-91 (2017) doi:10.1016/j.apm.2017.05.030 |
| [8] | SHI, W. C. Collinear periodic cracks and/or rigid line inclusions of antiplane sliding mode in onedimensional hexagonal quasicrystal. Applied Mathematics and Computation, 215(3), 1062-1067 (2009) doi:10.1016/j.amc.2009.06.055 |
| [9] | AKMAZA, H. K. and AKINCI, Ü. On dynamic plane elasticity problems of 2D quasicrystals. Physics Letters A, 373(22), 1901-1905 (2009) doi:10.1016/j.physleta.2009.03.065 |
| [10] | SLADEK, J., SLADEK, V., and PAN, E. Bending analyses of 1D orthorhombic QC plates. International Journal of Solids and Structures, 50, 3975-3983 (2013) doi:10.1016/j.ijsolstr.2013.08.006 |
| [11] | TUPHOLME, G. E. An antiplane shear crack moving in one-dimensional hexagonal quasicrystals. International Journal of Solids and Structures, 71, 255-261 (2015) doi:10.1016/j.ijsolstr.2015.06.027 |
| [12] | THIEL, P. A. and DUBOIS, J. M. QCs reaching maturity for technological applications. Materials Today, 2, 3-7 (1999) |
| [13] | RAMA, K., RAO, M., RAO, P. H., and CHAITANYA, B. S. K. Piezoelectricity in quasicrystals:a group-theoretical study. Pramana, 68, 481-487 (2007) doi:10.1007/s12043-007-0051-3 |
| [14] | ALTAY, G. and DÖMECI, M. C. On the fundamental equations of piezoelasticity of quasicrystal media. International Journal of Solids and Structures, 49, 3255-3262 (2012) doi:10.1016/j.ijsolstr.2012.06.016 |
| [15] | LI, X. Y., LI, P. D., WU, T. H., SHI, M. X., and ZHU, Z. W. Three-dimensional fundamental solutions for one-dimensional hexagonal quasicrystal with piezoelectric effect. Physics Letters A, 378, 826-834 (2014) doi:10.1016/j.physleta.2014.01.016 |
| [16] | ZHANG, L. L., ZHANG, Y. M., and GAO, Y. General solutions of plane elasticity of onedimensional orthorhombic quasicrystals with piezoelectric effect. Physics Letters A, 378, 2768-2776 (2014) doi:10.1016/j.physleta.2014.07.027 |
| [17] | YU, J., GUO, J. H., PAN, E. N., and XING, Y. M. General solutions of plane problem in one-dimensional quasicrystal piezoelectric materials and its application on fracture mechanics. Applied Mathematics and Mechanics (English Edition), 36(6), 793-814 (2015) doi:10.1007/s10483-015-1947-6 |
| [18] | YU, J., GUO, J. H., and XING, Y. M. Complex variable method for an anti-plane elliptical cavity of one-dimensional hexagonal piezoelectric quasicrystals. Chinese Journal of Aeronautics, 53, 1287-1295 (2015) |
| [19] | YANG, J. and LI, X. Analytic solutions of problem about a circular hole with a straight crack in one-dimensional hexagonal quasicrystals with piezoelectric effects. Theoretical and Applied Fracture Mechanics, 82, 17-24 (2016) doi:10.1016/j.tafmec.2015.07.012 |
| [20] | YANG, W. G., FEUERBACHER, M., TAMURA, N., DING, D. H., and WANG, R. H. Atomic model of dislocations in Al-Pd-Mn icosahedral quasicrystals. Philosophical Magazine A, 77, 1481-1497 (1998) doi:10.1080/01418619808214265 |
| [21] | LEVINE, D., LUBENSKY, T. C., OSTLUND, S., RAMASWAMY, S., and STEINHARDT, P. J. Elasticity and dislocations in pentagonal and icosahedral quasicrystals. Physical Review Letters, 54, 1520-1523 (1985) doi:10.1103/PhysRevLett.54.1520 |
| [22] | SOCOLAR, J. E. S., LUBENSKY, T. C., and STEINHARDT, P. J. Phonons, phasons and dislocations in quasicrystals, phasons and dislocations in quasicrystals. Physical Review B, 34, 3345-3360 (1986) |
| [23] | EDAGAWA, K. Elasticity, dislocations and their motion in quasicrystals. Dislocation in Solids, 13, 365-417 (2007) doi:10.1016/S1572-4859(07)80008-8 |
 2018, Vol. 39
2018, Vol. 39


