Shanghai University
Article Information
- Zhenhua XIA, Yipeng SHI, Qingdong CAI, Jie GAI
- Dissipation function in turbulent plane Poiseuille and Couette flows subject to spanwise rotations
- Applied Mathematics and Mechanics (English Edition), 2019, 40(2): 185-192.
- http://dx.doi.org/10.1007/s10483-019-2422-6
Article History
- Received Sep. 4, 2018
- Revised Oct. 8, 2018
2. State Key Laboratory for Turbulence and Complex Systems, Peking University, Beijing 100871, China;
3. CRRC Changchun Railway Vehicles Co., Ltd., Changchun 130062, China
Due to the ubiquity and importance in turbomachinery, the wall-bounded turbulent flow in a rotating reference frame has received a great deal of attention. Ever since the experimental investigations of a spanwise rotating plane Poiseuille flow (RPPF) conducted by Johnston et al.[1], it has been well accepted that the existence of the Coriolis force due to the system rotation will alter both the mean flow and the turbulent fluctuations[2]. In order to unravel the physics of turbulence in rotating wall-bounded flows, many studies were conducted on some typical flow categories with simple flow geometries, among which RPPFs and spanwise rotating plane Couette flows (RPCFs) are two canonical prototypes[3]. In an RPPF, since the mean vorticity changes its sign across the channel, the Coriolis force destabilizes the flow in part of the channel while stabilizes it in the other part. In contrast, the Coriolis force may either stabilize or destabilize the entire flow in the RPCF, since the mean velocity increases monotonically from one wall to the other in most situations.
In the past decades, many experimental and numerical studies have been carried out to investigate the effects of spanwise rotations on RPPFs and RPCFs. The experimental work for RPPFs[1, 4-5] and RPCFs[6-9] and the direct numerical simulation (DNS) for RPPFs[10-18] and RPCFs[19-24] are examples. Many flow characteristics, e.g., mean flow profiles, turbulence intensities, Reynolds shear stress, correlation coefficients, power spectra, and flow structures, were reported, which made them popular test cases for both the Reynolds-averaged Navier-Stokes (RANS) communities and the large-eddy simulation (LES) communities.
The mean energy dissipation rate per unit volume ϕ for incompressible flows has been widely studied. It is defined as follows[25]:
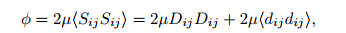
|
(1) |
where the standard Cartesian tensor notation and summation on repeated indices are used. ⟨·⟩ denotes the quantities averaged in the wall parallel directions as well as in the time. μ is the dynamic viscosity. Sij, Dij, and dij are the total, mean, and fluctuating parts of the velocity deformation tensor, respectively. The dissipation function Φ, which is defined as the integral of ϕ over the channel cross section, also has a mean part ΦM (the contribution from the mean shear) and a fluctuating part ΦT (the contribution from the turbulent fluctuations). It has been shown by Laadhari[26] and Abe and Antonia[27] that, in the turbulent plane Poiseuille flow (PPF) at a sufficiently high Reynolds number, ΦM+=ΦM/(ρuτ3), where 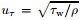
The aim of the present paper is to investigate the effects of the spanwise system rotation on the energy dissipation function in both RPPFs and RPCFs with available DNS databases. The remainder of the paper is organized as follows. The relationships for the dissipation function Φ in a RPPF, a turbulent plane Couette flow (PCF), and a RPCF are derived in Section 2. The results of Φ in a RPPF, a PCF, and a RPCF are presented and discussed in Section 3. A summary is given in Section 4.
2 Relationships for the dissipation function Φ in RPPF, PCF, and RPCFThe turbulent Poiseuille flow, RPPF, PCF, and RPCF are unidirectional, where the mean flow can be denoted as Ui(y)=(U(y), 0, 0). In the present work, x, y, and z or x1, x2, and x3 denote the streamwise, wall-normal, and spanwise coordinate directions, respectively, and u1, u2, and u3 are the velocity fluctuations in the corresponding directions; u, v, and w are used interchangeably with u1, u2, and u3. Following the derivation by Laadhari[26], we have
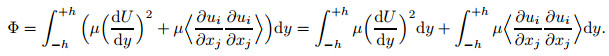
|
(2) |
Here, the first and second terms on the rightmost part of Eq. (2) are the mean part ΦM and the fluctuating part ΦT of the dissipation function Φ. According to the balance equation for the total turbulent kinetic energy across the channel, it is easy to obtain that
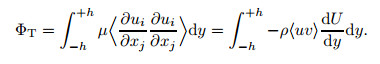
|
(3) |
In order to distinguish these two evaluations of ΦT, we denote the original definition ΦT, 1 and the calculation based on the turbulent kinetic energy production ΦT, 2. Then, we have
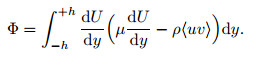
|
(4) |
In a turbulent PPF without system rotations, the total shear has the following form:
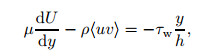
|
where τw is the mean wall shear stress. Thus,
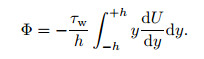
|
Applying the integration by parts and the no-slip boundary conditions at the walls, we have
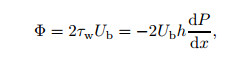
|
(5) |
where 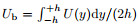
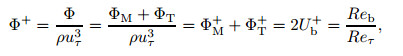
|
(6) |
where Reb=Ub2h/ν is the bulk Reynolds number. Laadhari[26] founded that ΦM+=18.27 while ΦT+=5.2 ln Reτ-14.17 when Reτ > 500. Therefore, Ub+ follows a logarithmic low when Ub+=A ln Reτ+B in which A=2.6 and B=2.05, and a relationship between Reb and Reτ can be obtained as follows: Reb=2Reτ(A ln Reτ+B). Abe and Antonia[27] found a similar logarithmic law for ΦT+ for Reτ≥300. However, the slope (5.08) and the intercept (-13.44) were different, and so were the constants A and B.
In the RPPF, the total shear has a different form as follows[10, 14, 16]:
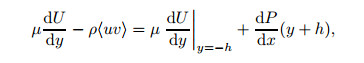
|
(7) |
where the mean pressure gradient
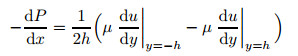
|
is constant at a fixed rotation number. Equations (4) and (7) lead to
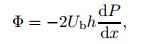
|
(8) |
which is the same as that in the PPF. In the RPPF, -dP/dx is directly related to the global wall friction velocity, i.e.,
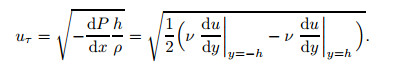
|
Thus, Eq. (6) can be achieved too if the global wall friction velocity is used.
In the PCF and RPCF, the total shear is constant across the channel[19, 21], i.e.,
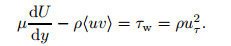
|
(9) |
Thus,
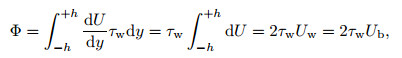
|
(10) |
where Uw is half of the wall velocity difference, which is approximately equal to the bulk velocity Ub in the PCF and RPCF. Again, Eq. (10) has the same expression as Eq. (5), which is a direct relationship coming from the energy conservation in a statistically stationary wall-bounded unidirectional turbulent flow. The nondimensionalized form is
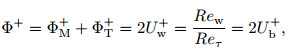
|
(11) |
where Rew=2hUw/ν.
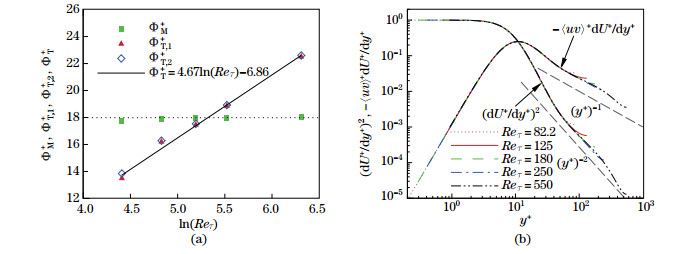
3 Results and discussion 3.1 Dissipation function Φ in PCFIn this subsection, we would like to present the dissipation function Φ in the PCF. The DNS data from Avsarkisov et al.[28] are used for the analysis. Avsarkisov et al.[28] presented a new set of DNS results in a large computational box at four Reynolds numbers, i.e., Reτ = 125, 180, 250, and 550. Figure 1(a) shows the mean shear ΦM+ and turbulent ΦT+ contributions to the nondimensionalized (using the friction velocity uτ) dissipation function Φ+=Φ/uτ3 of a PCF at five different Reτ in which the data are from Refs. [23] and [28]. It can be seen from the DNS data that ΦM+=18.0 is also a constant for all the five Reynolds numbers, while ΦT+, estimated from the integrations of both the turbulent energy production and the turbulent energy dissipation rate, follows a logarithmic law
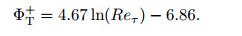
|
(12) |
|
| Fig. 1 (a) ΦM+, ΦT, 1+, ΦT, 2+, and ΦT+ from the PCF at different Reτ; (b) distributions of (dU+/dy+)2 and -⟨uv⟩+ dU+/dy+ of the PCF at five different Reτ in wall units (color online) |
|
|
The slope 4.67 is smaller than those for the PPFs estimated by Laadhari[26] and Abe and Antonia[27]. Furthermore, the values of ΦT+ from the PCF are larger than that from the PPF at the same Reτ if Reτ≤ 9.7×105. We attribute these deviations on the slope and values to the flow differences between the PPF and PCF. Avsarkisov et al.[28] showed the root mean square (RMS) velocity fluctuation profiles from the PPF and PCF at Reτ=550, and turned out that the off-wall intensities in all the three directions from the PCF are larger than those from the PPF for y+≥ 15. Higher turbulent intensities correspond to higher ΦT+.
It is interesting to notice that the constant behavior of ΦM+ exists at a much lower Reynolds number range in the PCF. This is not surprising, since the mean velocity follows a log law 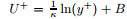
Figure 1(b) shows the distributions of (dU+/dy+)2 and -⟨uv⟩+ dU+/dy+ from the PCF at five different Reτ in wall units. It is clearly seen that, when y+≤30, the profiles of (dU+/dy+)2 and 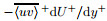
The dissipation function Φ+ in the PCF also follows a logarithmic law

|
(13) |
From Eq. (11), the dependence relationships of Uw+ and Rew on Reτ can be obtained, i.e.,
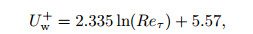
|
(14) |
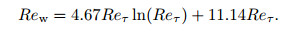
|
(15) |
In this subsection, we focus on the effects of spanwise system rotations on the energy dissipation function Φ in the RPPF and RPCF. For the RPPF, the DNS data at Reτ=180 based on the global friction velocity uτ[16] are used. The rotation number defined by the global friction velocity Roτ=2Ωh/uτ, where Ω is the constant angular velocity, varies from 0 to 130. The corresponding rotation number defined by the bulk velocity, i.e., Ro=2Ωh/Ub, varies from 0.000 to 2.287. The flow is driven by an imposed constant streamwise pressure gradient. For the RPCF, the DNS data at Rew=2 600[23] are used. The rotation number Ro=2Ωh/Uw varies from 0.0 to 0.9. Different from the RPPF, no constant streamwise pressure gradient is imposed in the RPCF, and the flow is driven by the relative movements of the two walls. For more details about the DNS descriptions and their validations, please refer to Refs. [16] and [23].
Figure 2 shows the nondimensionalized dissipation function Φ+ and its two shares, i.e., the mean shear contribution ΦM+ and the turbulent contribution ΦT+, in the RPPF at different Roτ. The results of twice of the mean bulk velocity in wall unit, i.e., 2Ub+, are also shown for comparison. It is seen from the figure that the deviations between 2Ub+ and Φ+ are negligible, which verifies the derivation of Eq. (6). When the rotation number increases in the range Roτ≤ 2.5, ΦM+ first increases, then decreases, reaches its minimum at about Roτ=10, and increases again. ΦT+ shows an opposite tendency. It first decreases with the rotation number when Ro ≤ 2.5, and then increases with it, reaching its peak value at about Ro = 40. After that, ΦT+ decreases with the rotation number.
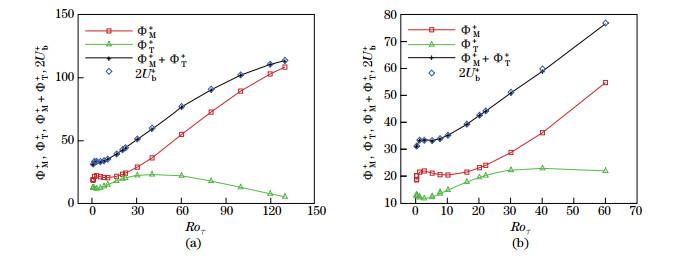
|
| Fig. 2 ΦM+, ΦT+, ΦM++ΦT+, and 2Ub+ for the RPPF at different Roτ: (a) 0≤ Roτ≤130; (b) zoomed-in results for 0≤ Roτ≤60 (color online) |
|
|
Figure 3 shows ΦT+, ΦM+, Φ+, and Uw+ in the RPCF at different Ro. The negligible deviations between Uw+ and Φ+ verify the derivation of Eq. (11). Different from the results obtained from the RPPF shown in Fig. 2, Φ+ obtained from the RPCF first decreases with Ro when Ro ≤ 0.15, and then increases. This difference might come from the different driving methods used in both cases. In the RPPF, the flow is driven by a constant mean pressure gradient, making sure of a constant global friction velocity, whereas in the RPCF, the flow is driven by the moving walls, resulting in a constant mean bulk velocity. The two shares, ΦM+ and ΦT+, also show different behaviors as compared with those from the RPPF. When Ro increases in the range Ro≤ 0.02, ΦM+ obtained from the RPCF first increases, then decreases rapidly until it reaches a plateau during 0.2≤ Ro≤0.6, and finally increases again. When Ro increases in the range Ro≤ 0.02, ΦT+ obtained from the RPCF first decreases, then increases until Ro=0.8, and finally decreases.
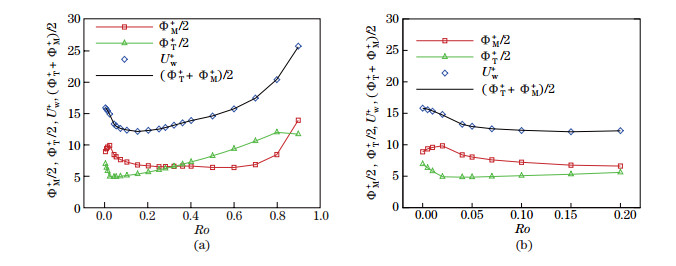
|
| Fig. 3 ΦM+/2, ΦT+/2, Uw+, and (ΦM++ΦT+)/2 for the RPCF at different Ro: (a) 0≤ Ro≤0.9; (b) zoomed-in results for 0≤ Ro≤0.2 (color online) |
|
|
The dissipation function has been studied in the turbulent PPFs without system rotations. It is believed that the approach based on dissipation can provide an interesting insight into the logarithmic skin friction law in PPFs. In this paper, we present the analysis on the dissipation function in the turbulent PPFs and PCFs subject to spanwise rotations.
Based on mathematical derivation, it is shown that the nondimensionalized forms of Φ are the same in the PPF and PCF with or without system rotations, although the total shear has different forms in the PPF and PCF. In all these problems, the dissipation function can be separated as two parts. One is the mean part ΦM+, and the other is the turbulent fluctuating part ΦT+. From this formula, we first study Φ in the PCF without system rotations. The results show that the mean part is constant while the fluctuation part follows a logarithmic law, resulting in a similar logarithmic skin friction law as the PPF. Furthermore, the log-law in the PCF is valid at about Reτ=80, which is much lower than that in the PPF, where Reτ is supposed to be larger than 300.
However, if the flow system rotates in the spanwise direction, no obvious dependence on the rotation number can be evaluated. In the RPPF, the dissipation function shows an increase in the rotation number, while in the RPCF, it first decreases and then increases with the rotation number. In the future, more data should be generated to study the dependence of the dissipation function on the rotation and Reynolds numbers.
| [1] |
JOHNSTON, J. P., HALLEEN, R. M., and LEZIUS, D. K. Effects of spanwise rotation on the structure of two-dimensional fully developed turbulent channel flow. Journal of Fluid Mechanics, 56, 533-559 (1972) doi:10.1017/S0022112072002502 |
| [2] |
JOHNSTON, J. P. Effects of system rotation on turbulence structure:a review relevant to turbomachinery flows. International Journal of Rotating Machinery, 4, 97-112 (1998) doi:10.1155/S1023621X98000098 |
| [3] |
JAKIRLIĆ, S., HANJALIĆ, K., and TROPEA, C. Modeling rotating and swirling turbulent flows:a perpetual challenge. AIAA Journal, 40, 1984-1996 (2002) doi:10.2514/2.1560 |
| [4] |
NAKABAYASHI, K. and KITOH, O. Low Reynolds number fully developed two-dimensional turbulent channel flow with system rotation. Journal of Fluid Mechanics, 315, 1-29 (1996) doi:10.1017/S0022112096002303 |
| [5] |
NAKABAYASHI, K. and KITOH, O. Turbulence characteristics of two-dimensional channel flow with system rotation. Journal of Fluid Mechanics, 528, 355-377 (2005) doi:10.1017/S0022112004002939 |
| [6] |
TILLMARK, N. and ALFREDSSON, P. H. Experiments on rotating plane Couette flow. Advances in Turbulence Ⅵ (ed(s). GAVRILAKIS, S., MACHIELS, L., and MONKEWITZ, P. A.), Kluwer, The Netherlands, 391-394(1996)
|
| [7] |
HIWATASHI, K., ALFREDSSON, P. H., TILLMARK, N., and NAGATA, M. Experimental observations of instabilities in rotating plane Couette flow. Physics of Fluids, 19, 048103 (2007) doi:10.1063/1.2716767 |
| [8] |
TSUKAHARA, T., TILLMARK, N., and ALFREDSSON, P. H. Flow regimes in a plane Couette flow with system rotation. Journal of Fluid Mechanics, 648, 5-33 (2010) doi:10.1017/S0022112009993880 |
| [9] |
KAWATA, T. and ALFREDSSON, P. H. Turbulent rotating plane Couette flow:Reynolds and rotation number dependency of flow structure and momentum transport. Physical Review Fluids, 1, 034402 (2016) doi:10.1103/PhysRevFluids.1.034402 |
| [10] |
KRISTOFFERSEN, R. and ANDERSSON, H. I. Direct simulations of low-Reynolds-number turbulent flow in a rotating channel. Journal of Fluid Mechanics, 256, 163-197 (1993) doi:10.1017/S0022112093002757 |
| [11] |
LAMBALLAIS, E., LESIEUR, M., and MÉTAIS, O. Effects of spanwise rotation on the vorticity stretching in transitional and turbulent channel flow. International Journal of Heat and Fluid Flow, 17, 324-332 (1996) doi:10.1016/0142-727X(96)00043-4 |
| [12] |
ALVELIUS, K. Studies of Turbulence and Its Modelling Through Large Eddy and Direct Numerical Simulation, Ph. D. dissertation, KTH Royal Institute of Technology, Sweden (1999)
|
| [13] |
LIU, N. S. and LU, X. Y. A numerical investigation of turbulent flows in a spanwise rotating channel. Computer and Fluids, 36, 282-298 (2007) doi:10.1016/j.compfluid.2005.11.004 |
| [14] |
GRUNDESTAM, O., WALLIN, S., and JOHANSSON, A. V. Direct numerical simulations of rotating turbulent channel flow. Journal of Fluid Mechanics, 598, 177-199 (2008) |
| [15] |
YANG, Y. T. and WU, J. Z. Channel turbulence with spanwise rotation studied using helical wave decomposition. Journal of Fluid Mechanics, 692, 137-152 (2012) doi:10.1017/jfm.2011.500 |
| [16] |
XIA, Z. H., SHI, Y. P., and CHEN, S. Y. Direct numerical simulation of turbulent channel flow with spanwise rotation. Journal of Fluid Mechanics, 788, 42-56 (2016) doi:10.1017/jfm.2015.717 |
| [17] |
DAI, Y. J., HUANG, W. X., and XU, C. X. Effects of Taylor-Görtler vortices on turbulent flows in a spanwise-rotating channel. Physics of Fluids, 28, 115104 (2016) doi:10.1063/1.4967702 |
| [18] |
BRETHOUWER, G. Statistics and structure of spanwise rotating turbulent channel flow at moderate Reynolds numbers. Journal of Fluid Mechanics, 828, 424-458 (2017) doi:10.1017/jfm.2017.526 |
| [19] |
BECH, K. H. and ANDERSSON, H. I. Secondary flow in weakly rotating turbulent plane Couette flow. Journal of Fluid Mechanics, 317, 195-214 (1996) doi:10.1017/S0022112096000729 |
| [20] |
BECH, K. H. and ANDERSSON, H. I. Turbulent plane Couette flow subject to strong system rotation. Journal of Fluid Mechanics, 347, 289-314 (1997) doi:10.1017/S0022112097006691 |
| [21] |
BARRI, M. and ANDERSSON, H. I. Computer experiments on rapidly rotating plane Couette flow. Communications in Computational Physics, 7, 683-717 (2010) |
| [22] |
SALEWSKI, M. and ECKHARDT, B. Turbulent states in plane Couette flow with rotation. Physics of Fluids, 27, 045109 (2015) doi:10.1063/1.4917281 |
| [23] |
GAI, J., XIA, Z. H., CAI, Q. D., and CHEN, S. Y. Turbulent statistics and flow structures in spanwise-rotating turbulent plane Couette flows. Physical Review Fluids, 1, 054401 (2016) doi:10.1103/PhysRevFluids.1.054401 |
| [24] |
XIA, Z. H., SHI, Y. P., CAI, Q. D., WAN, M. P., and CHEN, S. Y. Multiple states in turbulent plane Couette flow with spanwise rotation. Journal of Fluid Mechanics, 837, 477-490 (2018) doi:10.1017/jfm.2017.869 |
| [25] |
CORRSIN, S. Interpretation of viscous terms in the turbulent boundary energy equation. Journal of the Aeronautics Sciences, 20, 853-854 (1953) doi:10.2514/8.2881 |
| [26] |
LAADHARI, F. Reynolds number effect on the dissipation function in wall-bounded flows. Physics of Fluids, 19, 038101 (2007) doi:10.1063/1.2711480 |
| [27] |
ABE, H. and ANTONIA, R. A. Relationship between the energy dissipation function and the skin friction law in a turbulent channel flow. Journal of Fluid Mechanics, 798, 140-164 (2016) doi:10.1017/jfm.2016.299 |
| [28] |
AVSARKISOV, V., HOYAS, S., OBERLACK, M., and GARCIA-GALACHE, J. P. Turbulent plane Couette flow at moderately high Reynolds number. Journal of Fluid Mechanics, 751, R1 (2014) doi:10.1017/jfm.2014.323 |
| [29] |
LEE, C. B. Possible universal transitional scenario in a flat plate boundary layer:measurement and visualization. Physical Review E, 62, 3659-3671 (2000) doi:10.1103/PhysRevE.62.3659 |
| [30] |
LEE, C. B. and WU, J. Z. Transition in wall-bounded flows. Applied Mechanics Reviews, 61, 030802 (2008) doi:10.1115/1.2909605 |
| [31] |
SMITS, A. J., MCKEON, B. J., and MARUSIC, I. High-Reynolds number wall turbulence. Annual Review of Fluid Mechanics, 43, 353-375 (2011) doi:10.1146/annurev-fluid-122109-160753 |
| [32] |
MARUSIC, I, MONTY, J. P., HULTMARK, M., and SMITS, A. J. On the logarithmic region in wall turbulence. Journal of Fluid Mechanics, 716, R3 (2013) doi:10.1017/jfm.2012.511 |
 2019, Vol. 40
2019, Vol. 40


