Shanghai University
Article Information
- KANG Houjun, GUO Tieding, ZHU Weidong, SU Junyi, ZHAO Bingyu
- Dynamical modeling and non-planar coupled behavior of inclined CFRP cables under simultaneous internal and external resonances
- Applied Mathematics and Mechanics (English Edition), 2019, 40(5): 649-678.
- http://dx.doi.org/10.1007/s10483-019-2472-6
Article History
- Received Jun. 19, 2018
- Revised Oct. 3, 2018
2. Department of Mechanical Engineering, University of Maryland, Baltimore County, Maryland 21250, U. S. A;
3. College of Civil Engineering, Hunan University, Changsha 410082, China
Because of the advantages such as light weight, high strength, and flexibility, inclined cables have been widely used in many engineering fields, e.g., tower cranes, stayed bridges, guyed masts, and suspended roofs. Meanwhile, the investigation into the nonlinear dynamics of an inclined cable is a basic element for applied mechanics, and this long and rich history is documented in the classic monograph by Irvine[1] and summarized in Refs. [2]-[5]. Much work on different models[6], methods (numerical, theoretical, and experimental), and deterministic phenomena under external and/or internal resonances have been or are being conducted owing to the dynamical importance of inclined cables in the fields of mathematics, mechanics, and engineering. However, most existing studies focus on the traditional steel cables with in-plane excitations or forced and parametric excitations[7]. There are also many studies on the external and internal resonances of beams and plates[8-10]. Therefore, it is necessary to explore the dynamic behaviors of inclined cables subject to external and internal resonances.
Carbon fiber-reinforced plastic (CFRP) (cable and sheet) is a lightweight material with high strength and high corrosion resistance, and has been widely used in civil engineering, especially bridge engineering[11], e.g., the Herning Footbridge in Denmark and the Laroin Footbridge in France[12]. Kremidas[13], Kao et al.[14], Kou et al.[15], Fan et al.[16], and Xie et al.[17-18] studied the structures and the mechanical properties of CFRP cables, and investigated their applications in cable-stayed bridges. Although a significant amount of research on CFRP cables can be found in the literature, the studies on their dynamic behaviors are few. Kang et al.[19-20] developed a dynamic model for CFRP cables, and evaluated the nonlinear dynamic properties of stay cables subject to parametric and forced excitations. They showed that CFRP cables could reduce the large vibrations under subharmonic resonances because the variations in Young's modulus could change the softening or hardening characteristics of the CFRP cables. With the significant advantages such as higher strength and corrosion resistance compared with traditional steel cables, CFRP cables play a significant role in the construction of super-long span bridges. Therefore, it is both meaningful and interesting for the further understanding of both the linear and nonlinear dynamics of CFRP cables.
Considering both the linear and nonlinear dynamics of inclined CFRP cables under three types of external excitations (in-plane, out-of-plane, and both in-plane and out-of-plane), a dynamic model that considers the bending stiffness, the shear stiffness, and the thermal changes is established, and its eigenvalue issue and nonlinear dynamic behavior are investigated with the multiple scale method (MSM). Hamilton's principle is used to derive the nonlinear differential equations governing the motion of the inclined CFRP cables. Then, the two-dimensional (2D) model with the lowest in-plane and out-of-plane modes is obtained by the Galerkin integral, and the free vibrations of both the in-plane mode and the out-of-plane mode are investigated by parametric analyses. In order to roughly model the effect of wind loads on the dynamics of CFRP cables, ideal in-plane harmonic excitations and lateral harmonic excitations are applied respectively and simultaneously. The numerical technique is also used to obtain the frequency- and force-response curves to determine the nonlinear dynamics of the system for different parameters under simultaneous one-to-one internal resonances between the lowest in-plane and out-of-plane modes and the primary external resonances. In particular, Young's modulus is considered, which has an important effect on the spatial motion of the system. Lastly, some meaningful conclusions are presented in the final section.
2 Static responsesStatic response (profile) is one of the key factors affecting the dynamics of a cable. In order to investigate the dynamic characteristics of the inclined CFRP cable, we derive its static configuration in this section.
The shear force is considered for an inclined CFRP cable since its shear rigidity is relatively low compared with that of a steel cable. Therefore, the safety of large-scale structures is also considered. In the present study, we consider not only the shear rigidity and the flexural rigidity but also the thermal effects on the nondimensional model of the static response of inclined CFRP cables. Temperature changes will affect the dynamic behavior since the static configuration is sensitive to temperature[21].
Figure 1(a) displays an inclined CFRP cable with an arbitrary inclination angle θ in a fixed Cartesian coordinate (x, y) system, where l denotes the length without gravity, and s represents the curvilinear coordinate. A free-body diagram of an infinitesimal element of the inclined CFRP cable is shown in Fig. 1(b), where H, M, and Q denote the tension (axial) force, the bending moment, and the shear force, respectively. Here, the sag of the inclined CFRP cable is very small because its density is less than one-fifth that of the steel cable. Hence, the directions of the tension force and the shear force are set along the axial directions of x and y, respectively.
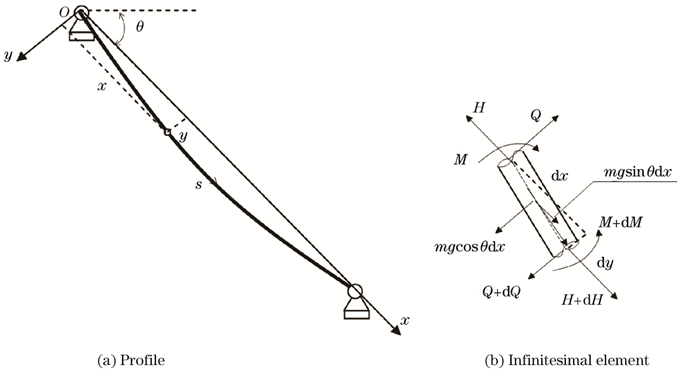
|
| Fig. 1 Static configuration of the inclined CFRP cable |
|
|
Figure 1(b) shows the static equilibrium equation in the x-direction as follows:
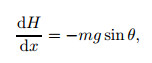
|
(1) |
where ds≈ dx.
Integrating Eq. (1), we have
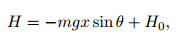
|
where H0 denotes the initial tension force. Generally, we have
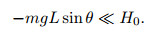
|
Therefore, we ignore the errors between H and H0, i.e., H=H0.
Similarly, the equilibrium equation in the y-direction is
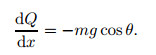
|
(2) |
The moment balance equation of the infinitesimal element in Fig. 1(b) can be expressed as follows:

|
(3) |
Differentiating the above equation once yields

|
(4) |
Substitute Eq. (2) into Eq. (4). Since
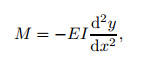
|
(5) |
we have

|
(6) |
where E is Young's modulus, and I is the second moment of the area of the cross-section. Equation (6) is the differential equation indicating the static profile of the inclined CFRP cable. It should be noted that Eq. (6) represents the static profile of a suspended CFRP cable with two horizontal ends when θ=0.
The dimensionless variables are defined as follows:

|
(7) |
Substituting Eq. (7) into Eq. (6) gives

|
(8) |
where, for brevity, the overbar is deleted, and

|
(9) |
The solution that we are interested in is the one satisfying the boundary conditions of zero translational and angle displacements at each end, suggesting that the bending stiffness of the inclined CFRP cable is considered. The boundary conditions of zero displacement and bending moment at each end are obtained in Ref. [1].
In dimensionless form, the solution for the clamped-clamped ends is

|
(10) |
The solution for the hinged-hinged ends is

|
(11) |
The physical parameters of the inclined CFRP cable are given as follows:
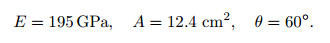
|
Figure 2 shows the effects of the length and the tension force of the inclined CFRP cable on its sag errors of the midspan with two different boundary conditions. The sag error is evident when the tension force is small for both short and long cables. It rapidly decreases when the tension force increases. The error is negligible when the tension force is greater than 60 kN. Figure 3 shows that the static profiles with different boundary conditions are different, especially near the two ends. An obviously bending deformation exists when the boundary condition is clamped-clamped, but no bending deformation occurs in the other case. Therefore, it is more adaptive if the two ends are modeled under the clamped-clamped conditions since the steel cable almost cracks near the two ends in practice.

|
| Fig. 2 Effects of the length and the tension force of the inclined cable on its sag errors of the midspan with different boundary conditions |
|
|

|
| Fig. 3 Static profiles of an inclined cable with different boundary conditions, where L = 50 m, and H = 15.6 kN |
|
|
In order to consider the effect of the thermal change of the inclined CFRP cable or steel cable on its dynamic behavior, it is assumed that the ambient temperature is constant when vibrations occur. This is because the change of temperature is a gradual process but vibrations occur suddenly under certain conditions. The thermal expansion coefficient α is introduced in the initial tension force H0, i.e., H0 =Ex A(ε0 -α ΔTint), where ΔTint is the increment of temperature. The effects of the thermal change on the static profile and the dynamics of the inclined CFRP cable are important, and will be discussed in the following section.
3 Governing equations of the inclined CFRP cableIn this section, we consider the inclined CFRP cable whose geometry can be described by three different configurations (see Fig. 4). The three configurations are (ⅰ) a natural state So with the initial tension, which can be described through the Cartesian abscissa x1; (ⅱ) a static deformed shape SI under the dead load and temperature variation, which can be illustrated by the curvilinear abscissa sI; (ⅲ) a dynamic configuration SV due to the motion of the inclined CFRP cable, which can be depicted by the curvilinear abscissa sV and denoted by εV of the total Lagrangian strain. Note that the static deformation component SI starting from the natural shape So has been discussed in the previous section. Here, ui (u1 =u; u2 =v; u3 =w) is used to describe the dynamic displacement of the inclined CFRP cable starting from the static deformed shape SI. A Cartesian reference system O-x1x2x3 is used to depict the positions for the static shape xiI and the dynamic shape xiV. θ is the inclined angle of the inclined CFRP cable versus the horizontal plane.

|
| Fig. 4 Inclined CFRP cable configuration, where So is the natural state, SⅠ is the static deformed shape, and SV is the dynamic deformed shape |
|
|
The strain energy of the inclined CFRP cable can be written as follows:

|
(12) |
where

|
(13) |
and ExA, ExI, and GA denote the axial stiffness, the bending stiffness, and the shearing rigidity, respectively. κ represents a reduced area coefficient of the cross-section corresponding to the shear force, and κ = 1 is the reduced area coefficient of the circle cross-section. γi (i=2, 3) are the shear angles, i.e.,
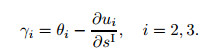
|
θi (i=2, 3) are the cross-sectional rotation angles due to bending. The torsional angle is ignored since the twist is generally negligible for the stay cables in bridges when the wind is regarded as an ideal harmonic load. On the right-hand side of Eq. (12), the first term ΠI is the elastic potential energy of the inclined CFRP cable corresponding to the static deformed shape, the second term represents the work done by the initial tension force and dynamic axial force, the third term denotes the work done by the bending moment, the fourth term indicates the work done by the shearing force introduced in bending deformation, and the last term indicates the potential energy of gravity.
The kinetic energy Ek and the virtual work W of the inclined CFRP cable should be considered to obtain the governing equation. In what follows, the cable will be used to replace the inclined CFRP cable. Considering the rotational inertia, the kinetic energy and the virtual work can be expressed as follows:

|
(14) |

|
(15) |
where m is the mass density per unit length of the cable, μi is the viscous damping, ρ is the volume density of mass, and pi is the distributed external load in the x-, y-, or z-direction. In Eq. (15), the first term represents the virtual work done by the forced excitation, and the second term denotes the virtual work done by the damping force.
The extended Hamilton's principle can be stated as follows:

|
(16) |
Considering the boundary conditions, we have

|
(17) |
Substituting Eqs. (12), (14), and (15) into Eq. (16), the following equations of motion for the cable can be obtained while accounting for bending and shearing the rigidity and thermal variations:

|
(18) |

|
(19) |

|
(20) |

|
(21) |

|
(22) |
The hypothesis dsI≈ dx is used in the derivation process. Note that Eq. (20) will yield an additional strain expression if we ignore the terms representing the inertial forces, the damping forces, and the external forces along the x-direction[22]. If the rotational inertia and shear stiffness terms are ignored, Eqs. (18)--(22) can be simplified into the equations obtained by Ricciardi and Saitta[23]. According to the boundary conditions and recalling Eq. (13), we can rewrite Eq. (20) as follows:

|
(23) |
The 2D integral differential equations can be obtained from Eqs. (18)-(23) as follows:

|
(24) |
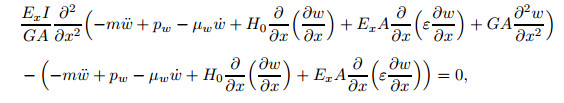
|
(25) |
where the rotational inertia term and the joint term of the rotational inertia and the shear stiffness are negligible. These two equations govern the motion of the cable, and are identical to those of a suspended CFRP cable except under the static state.
Introduce the following nondimensional quantities:
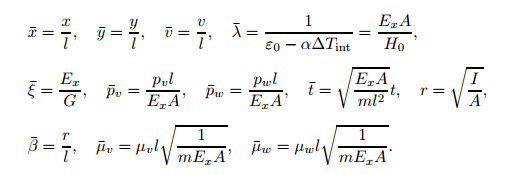
|
Then, Eqs. (24) and (25) can be rewritten as follows:

|
(26) |

|
(27) |
Similarly, Eq. (23) can be rewritten as follows:

|
(28) |
Let

|
(29) |

|
(30) |
Substituting Eqs. (29) and (30) into Eq. (28), we have

|
(31) |
where

|
Substituting Eqs. (29) and (30) into Eqs. (26) and (27) and then applying the Galerkin integral yield

|
(32) |

|
(33) |
where
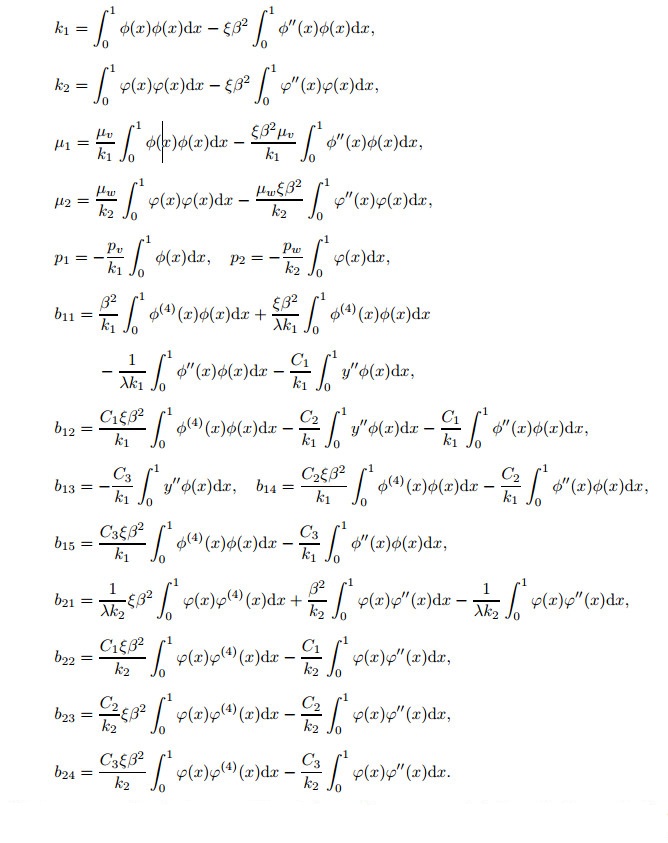
|
The in-plane and out-of-plane differential equations are coupled through the quadratic and cubic nonlinear terms arising from the stretching of the cable centerline (see Eq. (31)). In the following section, we will focus on the eigenvalues of the system.
4 Free vibrations 4.1 In-plane vibrationsIn this section, the in-plane free vibrations including the frequencies and the modal shapes of the considered cable are discussed. The following terms are ignored: the out-of-plane displacement w, the external force, the damping force, the rotational inertia term, and the joint term of the rotational inertia and the shear stiffness on the free vibrations of the cable. Then, Eq. (26) leads to

|
(34) |
where the temperature term is considered, and 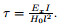
Similarly, Eq. (11) can be rewritten as follows:

|
(35) |
where

|
The second term in Eq. (11) is ignored because it is a higher-order term but is smaller than the first one[1]. Therefore, the initial static configuration of the cable is assumed as Eq. (35).
The boundary conditions can be rewritten as follows:

|
(36) |
Let

|
where ω is the angular frequency. Then, substituting it and Eq. (35) into Eqs. (34) and (36) yields

|
(37) |

|
(38) |
where
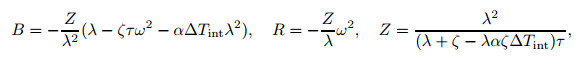
|
Γ is an unknown constant expressed by
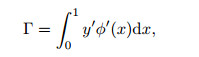
|
and D is the differential operator (D(·)=d(·)/dx).
(Ⅰ) When Γ =0, Eq. (37) is a homogeneous differential equation with the solution

|
(39) |
where Ci (i=1, 2, 3, 4) are constants, and

|
(40) |
In this case, ϕ (x) corresponds to the antisymmetrical mode of the cable. To simplify the expression of frequencies and modal shapes, the coordinate origin is moved to the middle point of the cable span. Hence, Eq. (38) has the following new form:

|
(41) |
According to the boundary conditions in Eq. (41) and the antisymmetrical modes of the cable, we can get that the two constants C1 and C3 must be zero, and

|
(42) |

|
(43) |
The two unknown constants C2 and C4 are nontrivial only if the coefficient matrix of the above two equations has a zero determinant, which leads to

|
(44) |
This is the nondimensional frequency equation of the in-plane antisymmetrical modes of the cable with the consideration of the bending, shear stiffness, and thermal effects. Substitute Eq. (42) into Eq. (39). Then, we obtain the nondimensional modal shape function as follows:

|
(45) |
(Ⅱ) When Γ ≠ 0, Eq. (37) is a nonhomogeneous differential equation with the solution
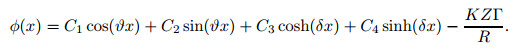
|
(46) |
This case corresponds to the symmetrical modes of the cable, i.e., C2=0 and C4=0 when the coordinate origin is moved to the middle point of the cable span.
According to the boundary conditions shown in Eq. (41), we get

|
(47) |

|
(48) |
where
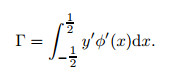
|
Substituting Eq. (46) and

|
into Γ yields

|
(49) |
Substituting the solution of Eqs. (47) and (48) into Eq. (46), we can obtain the modal shape function of the in-plane symmetrical modes as follows:

|
(50) |
The unknown constants C1, C3, and Γ can be derived in a nontrivial manner only if the coefficient matrix of Eqs. (47)-(49) has a zero determinant. Expand the determinant. Then, we can obtain the nondimensional frequency equation as follows:

|
(51) |
The modal frequency equations and shape functions of the in-plane symmetrical and antisymmetrical modes of the cable are obtained, which covers the effects of the initial tension force, the thermal changes, the bending stiffness, the shearing, and the ratio of Young's modulus to the shear modulus on the dynamical characteristics.
4.2 Out-of-plane free vibrationIn this section, the out-of-plane free vibrations, including the modal frequencies and shapes of the cable, are discussed. Similar to Subsection 4.1, ignoring the following terms: the in-plane displacement v, the external force, the damping force, the quadratic term of w, the rotational inertia term, and the joint term of rotational inertia and shear stiffness on the out-of-plane free vibration of the cable, we can rewrite Eq. (27) as follows:

|
(52) |
The boundary conditions can be rewritten as follows:

|
(53) |
Set w(x, t)=φ (x)exp(iωt), where ω is the angular frequency. Substituting it into Eqs. (52) and (53) yields

|
(54) |

|
(55) |
where
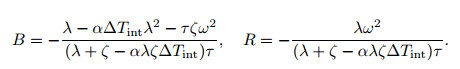
|
For the homogeneous ordinary differential equation shown in Eq. (54), using the classical procedure[24] yields a solution similar to Eq. (46).
We move the coordinate origin to the middle point of the cable span. Then, the boundary conditions in Eq. (55) have the following new form:

|
(56) |
Substituting Eq. (46) into the boundary conditions in Eq. (56) yields

|
(57) |

|
(58) |

|
(59) |

|
(60) |
Setting C2 =0 and C4 =0 and imposing the boundary conditions yield

|
(61) |

|
(62) |
which are the frequency equation and the modal shape function of the out-of-plane symmetrical mode, respectively.
Setting C1 =0 and C3 =0 and imposing the boundary conditions yield

|
(63) |

|
(64) |
which are the frequency equation and the modal shape function of the out-of-plane antisymmetrical mode, respectively.
As shown in Eqs. (61)-(64), the key parameters such as ζ, β, ε0, and ΔTint have a significant effect on the out-of-plane free vibration of the cable.
4.3 DiscussionIn this section, we focus on the effects of the key parameters, e.g., the ratio of Young's modulus to the shear modulus ζ, the nondimensional bending stiffness τ, the initial tension strain ε0, the temperature increment ΔTint, and the elasto-geometric parameter λ, on the symmetrical/antisymmetrical frequencies of the lowest in-plane/out-of-plane modes of the cable. The parametric study is conducted by means of the proposed expressions through the MATHEMATICA software.
The cable ends are anchored at different levels and fixed by the applied initial force H0 =1.2× 106 N at different temperatures. The cable has the following characteristics:
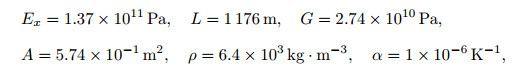
|
where Ex is the initial value of the axial Young's modulus, which can vary from 137 GPa to 1 000 GPa. The initial temperature is 273.15 K. The other nondimensional parameters can vary based on the above properties. Figure 5(a) shows the variations in the tension force of the cable, where ε0 is a function of temperature, and is set to be 0.001~5, 0.001~6, and 0.001~7, respectively. The temperature significantly affects the tension force. Especially, the sensitivity of the tension force to the temperature is different, which depends on the initial strain. Moreover, the tension force of a lower initial strain is more sensitive to the temperature than that of a higher initial strain. This is due to the fact that the strain produced by thermal variations is a big part of the total strain when the initial strain is small. Figure 5(b) plots the in-plane static configurations of the cable at different temperatures. It is noted that the sag increases when the temperature rises. This is due to the fact that, when the temperature increases, the tension force decreases while its sag increases.

|
| Fig. 5 Effects of the temperature on the tension force and the static configuration |
|
|
Figure 6 shows the in-plane modal frequency spectra with different values of the elasto-geometric parameter λ of the cable. The antisymmetrical and symmetrical modal frequency spectra are denoted by dotted and solid lines, respectively. The crossover and avoidance phenomena occur when the Irvine parameter increases. As shown in Fig. 6(a), the antisymmetrical and symmetrical modal frequencies depend on the parameter λ. This is different from Irvine's result[1], where the antisymmetrical mode is independent of λ. When λ increases, the frequency spectrum curves become horizontal, approaching the frequency of an inextensible cable. The crossover and avoidance points in Fig. 2(a) are different from those given in Ref. [20] because both the shear stiffness and the bending stiffness are considered in the dynamical model of the cable. Further discussion on the crossover and shape of the first symmetrical mode is carried out (see Fig. 6(b)). As can be seen from Fig. 6(b), if λ < λ1 (λ1=1 509), the frequency of the first symmetric mode is less than that of the first antisymmetric mode, and the vertical component of the first symmetric mode shape has no internal node, which is similar to the results given by Irvine[1]. If λ =λ1, the frequencies of the first symmetric and antisymmetric modes are not equal, which is a new phenomenon, compared with Irvine's result[1]. In this case, the vertical modal component is tangential to the profile at the supports. Here, λ1 can be defined as a critical point of the mode shape (CPMS), at which the mode shape transforms from no internal node to many internal nodes or vice versa. The frequency of the first symmetric mode is less than the frequency of the first antisymmetric mode when λ1 < λ < λ2 (λ2=1 799). However, two internal nodes appear in the vertical component of the first symmetric mode shape. Moreover, if λ =λ2, the frequencies of these two modes are equal. λ2 can be defined as the crossover point of the frequency (CPF). When λ >λ2, the frequency of the symmetric mode is larger than that of the antisymmetric mode. The discussion shows that the CPMS and the CPF are different, but they are identical in Ref. [1]. This could be attributed to the fact that the dimensionless bending stiffness is considered in the dynamical model, which is similar to the buckling change mode from a C-curve to an S-curve when the spring stiffness bears a certain relation to the flexural stiffness.

|
| Fig. 6 Relationships between the in-plane modal frequencies and the elasto-geometric parameter λ of the cable |
|
|
Figure 7(a) illustrates the natural frequencies of the in-plane modes as a function of the ratio ζ of Young's modulus to the shear modulus at different temperatures. It is well-known that Young's modulus of the CFRP cables ranges from 137 GPa to 1~000 GPa, or even greater than 1~000 GPa, while the shear modulus is relatively small. Young's modulus can be selected to match different types of demands under special environmental conditions. From the curves shown in Fig. 7(a), it can be seen that the natural frequencies may increase or decrease with the increase in ζ at different temperatures. At higher temperatures, i.e., ΔTint = 30 K, the natural frequencies of the lower modes decrease when ζ increases, e.g., the first three order symmetric modes and the first four order antisymmetric modes. However, the natural frequencies of higher modes increase when ζ increases. The natural frequencies of the fourth symmetrical mode is a critical mode since its frequency trends a limit after increasing and crossing the frequency of the fourth antisymmetric mode when ζ increases. The critical modes are different at different temperatures. The first antisymmetric mode becomes the critical mode when ΔTint = 0 K. These features make the design of the CFRP cable complex, especially with regard to the vibration control. When the temperature is below zero, e.g., ΔTint = -30 K, all the natural frequencies of the in-plane modes increase when ζ increases.

|
| Fig. 7 Relationships between the frequencies of the in-plane modes and ζ at different ΔTint and the fifth symmetric and antisymmetric modes |
|
|
The crossover phenomena between the symmetric and antisymmetric modes and the avoidance phenomena between the symmetrical modes are also observed. It is worth noting that the crossover between the fifth-order symmetrical and antisymmetrical modes produces twice when the ratio ζ increases. Simultaneously, the mode shape varies with increasing ζ (see Fig. 7(b)). If ζ < 7.5, the frequency of the fifth symmetric mode is less than that of the fifth antisymmetric mode, and the vertical component of the fifth symmetric mode shape has eight internal nodes. When ζ = 7.5, the mode shape has no internal node and is tangential to the profile at the supports, which indicates that ζ = 7.5 is a CPMS. When

|
the frequency of the fifth symmetric mode is also less than that of the fifth antisymmetric mode, and the mode shape has no internal node. When ζ further increases, the CPF and CPMS appear sequentially.
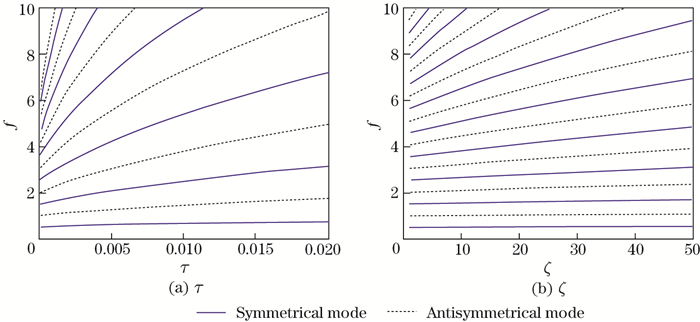
The effects of the key parameters, e.g., the elasto-geometric parameter λ, the bending stiffness τ, and the ratio ζ of Young's modulus to the shear modulus on the natural frequencies of the out-of-plane modes, are discussed. Figure 8 depicts the natural frequencies of the out-of-plane modes of the cable. It shows that the natural frequencies of the out-of-plane modes are not sensitive on the elasto-geometric parameter λ since these frequencies remain almost constant when the elasto-geometric parameter λ increases. However, the frequencies are susceptible to the bending stiffness τ, the ratio ζ of Young's modulus to the shear modulus, and the temperature (see Figs. 9(a) and (b)). Figure 9(a) shows that the natural frequencies of the high-order modes increase sharply when the bending stiffness increases from 0 to 0.002 5. We take the fourth symmetrical mode as an example, when the bending stiffness is 0.002 165, the natural frequency increases by 48.9% from 3.667 to 5.460. Therefore, we can conclude that the bending stiffness is a key factor for understanding the dynamic behavior of the cable, which is similar to the previous work on the steel cable in Ref. [25]. It is well-known that the bending stiffness is constant for a designed CFRP cable or steel cable and is difficult to be changed, since it is determined by the transverse size of the cross-section. In order to obtain the desired natural frequencies for controlling the large vibration of the cable, a reasonable ζ may be important. As shown in Fig. 9(b), the natural frequencies of higher-order modes are also sensitive to ζ. In addition, it is clear that the natural frequencies of lower-order modes, including the first two symmetric and antisymmetric modes, increase slightly when ζ increases.

|
| Fig. 8 Relationship between the frequency of the out-of-plane modal and the elasto-geometric parameter λ of the inclined CFRP cable |
|
|
|
| Fig. 9 Relationships between the frequency of the out-of-plane mode and the parameters τ and ζ |
|
|
In the following section, we will discuss the spatial motion of the cable so as to understand its nonlinear dynamical behavior.
5 Perturbation analysisIn this section, the standard MSM[26-28] is directly applied to the governing equations (32) and (33) for determining the equilibrium solution of the cable under external primary and one-to-one internal resonances.
Equations (32) and (33) can be rewritten as follows:

|
(65) |

|
(66) |
where pi (i=1, 2) are replaced by the harmonic loads ficos(Ωit) (i=1, 2), and
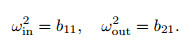
|
A bookkeeping parameter ε, which is later set to be 1, is introduced to rescale the parameters governing these equations, including the nonlinear terms, the damping terms, and the external load. The apex denotes the differentiation with respect to the time t.
The displacements g(t) and q(t) are expanded as follows:

|
(67) |

|
(68) |
where

|
Substituting Eqs. (67) and (68) into Eqs. (65) and (66) and then equating the coefficients of the same powers of ε, we obtain the following differential equations:
(ⅰ) ε0

|
(69) |

|
(70) |
(ⅱ) ε1

|
(71) |

|
(72) |
where

|
The general solutions of Eqs. (69) and (70) can be expressed as follows:

|
(73) |

|
(74) |
where Aj(T1) (j=1, 2) are complex functions, and Bj (T1) is the corresponding conjugate complex function of Aj(T1).
Substituting Eqs. (73) and (74) into Eqs. (71) and (72), we have

|
(75) |
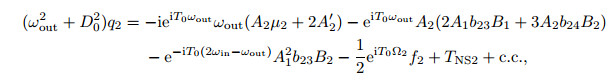
|
(76) |
where TNSj(j=1, 2) denote the non-secular terms, c.c. denotes the complex conjugate of the preceding term, and the apex denotes differentiation with respect to T1.
For the external primary and internal one-to-one resonances of the system,

|
(77) |
where j=1, 2, aj and ψj are the amplitude and phase of Aj, respectively.
5.1 In-plane excitationTo explore the internal one-to-one resonance between both modes of the system under the external primary resonance of the lowest in-plane mode, we let

|
(78) |
By substituting Eqs. (77) and (78) into the secular terms in Eqs. (75) and (76) and separating the real and imaginary parts, we obtain the modulation equations in polar form for the internal one-to-one resonance between both modes when the external primary resonance of the in-plane mode occurs as follows:

|
(79) |

|
(80) |

|
(81) |

|
(82) |
where

|
In the above equations, σ and σ1 are the external and internal detuning parameters, respectively.
5.2 Out-of-plane excitationTo explore the internal one-to-one resonance between the lowest in-plane and out-of-plane modes of the cable applied with the lateral excitation, we let

|
(83) |
Substituting Eqs. (77) and (83) into the secular terms in Eqs. (75) and (76) and separating the real and imaginary parts, we obtain the modulation equations in polar form for the internal one-to-one resonance between both modes when the external primary resonance of the out-of-plane mode occurs as follows:

|
(84) |

|
(85) |

|
(86) |

|
(87) |
where
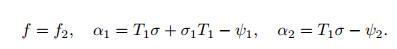
|
For the loads added in both the in-plane and the out-of-plane modes, the dynamic behavior of the cable under the condition of internal one-to-one resonance could be more interesting. Similarly, we let

|
(88) |
Substituting Eqs. (77) and (88) into the secular terms in Eqs. (75) and (76), we can obtain the modulation equations in polar form for the internal one-to-one resonance as the external primary resonance of both the first in-plane and out-of-plane modes occurring as follows:

|
(89) |

|
(90) |

|
(91) |

|
(92) |
where
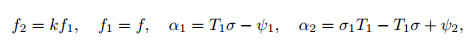
|
and k is a dimensionless factor.
In this section, the modulation equations in polar form for the internal one-to-one resonance of the cable are derived by the standard MSM. The nonlinear dynamic behavior of the system will be discussed in the following section.
6 Nonlinear dynamic behaviorsIn this section, the nonlinear dynamic behaviors of the system are discussed in detail when the internal one-to-one resonance between the lowest in-plane and out-of-plane modes of the cable is subject to different external harmonic excitations.
6.1 Physical parameters of the cablesIn order to explore the nonlinear dynamic behavior of the cable under the conditions of internal and external resonances with different materials, excitation frequencies, and amplitudes using the aforementioned detuning equations, we choose the basic dimensional and physical parameters of the steel cable as follows:
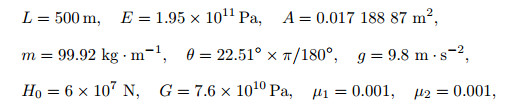
|
where L is the length, E is Young's modulus, A is the cross-sectional area, m is the mass per unit length, θ is the inclined angle, g is the gravity acceleration, H0 is the initial tension force, G is the shear modulus, and μ1 and μ2 are damping ratios. Equations (50) and (62) are the lowest mode shapes of the in-plane and out-of-plane of the steel cable, respectively. Thus, the first dimensional frequencies of the in-plane and out-of-plane of the cable are 0.149 4 and 0.132 9, respectively. In addition, the materials CFRP1 and CFRP2 will be used to explore the nonlinear dynamic behaviors of the CFRP cable. The physical parameters are given as follows: the shear modulus is 5.3×1010 Pa, the density per unit length is 20.29 kg·m-1, and Young's modulii are 1.95×1011 Pa and 5.95×1011 Pa for CFRP1 and CFRP2, respectively.
In the following figures, the frequency-response and force-response curves are used to investigate the dynamic behaviors of the system. The dotted and solid lines denote the unstable and stable solutions, respectively. SN denotes a saddle node bifurcation, while HB represents a Hopf one. To reduce the number of figures, the solutions a1 and a2 have been merged into one figure, and a2 is sometimes replaced by -a2.
6.2 External primary resonances of the in-plane modeFigure 10 shows the frequency-response curves of cables with different excitation forces and materials when excitation is applied to the in-plane mode. There are no unstable branches and no single in-plane modal motion for the given cases. The response amplitude of the in-plane mode is always larger than that of the out-of-plane mode. Although the response amplitude increases with the increase in the excitation force of the cable, the resonance frequency range moves far away from the natural frequency and initial conditions, i.e., the initial displacements or speeds need to be increased. Comparing Figs. 10(a), 10(b), and 10(c), we can conclude that it is useful to replace the steel cable with a CFRP one since it makes the occurrence of the primary resonance more difficult. For example, as seen in Fig. 10, the detuning parameter σ shifts from 0.186 7 to 0.351 1 when the steel cable is replaced by CFRP2 and f=0.01.

|
| Fig. 10 Frequency-response curves of cables with different materials |
|
|
Figure 11 shows the force-response curves of cables with different excitation forces and materials when the excitation is applied to the in-plane mode. It can be seen that there exist multiple branches of equilibrium solutions within a small range of excitation forces when the corresponding excitation frequency is fixed; the bigger the excitation frequency is, the larger the range of excitation forces inducing external primary resonances is. Furthermore, although there are two stable branches if the excitation force is within a very small range, the dynamic behavior is complex. Figure 11 shows the Hopf bifurcations (HB1 and HB2) and saddle node bifurcations (SN1, SN2, and SN3). Large vibrations may occur when the excitation force is within a certain range between the corresponding excitation forces producing HB1 and HB2. In addition, the excitation force range, in which the multiple branches of the equilibrium solutions are observed, decreases when the CFRP2 cable is used to replace the steel cable. Generally, the large vibrations generated by the external primary and internal resonances occur easily within this excitation force range. Therefore, the CFRP cable can be used to replace the steel cable to reduce the possibility of large vibrations by reducing the excitation force range inducing the external primary and internal resonances from the view point of nonlinear dynamics.

|
| Fig. 11 Force-response curves of cables with different materials (color online) |
|
|
Figure 12 shows the frequency-response curves of the steel cable with different excitation forces when excitation is applied to the out-of-plane mode. There are four branches of equilibrium solutions within a certain excitation frequency range when f=0.000 1, but there are only two branches when f=0.001. In other words, the dynamics of the system becomes relatively simpler when the excitation force increases. In addition, it is seen that there exists a trivial solution only for the in-plane response a1, while there is no trivial solution for the out-of-plane response a2. This means that the single modal response can be excited when the excitation is applied to the out-of-plane mode, which is different from the result obtained in Subsection 6.2. This phenomenon can also be observed in Fig. 13 when the CFRP cable is used to replace the steel cable. Similar to the results obtained by the in-plane excitation, increasing the excitation force and replacing the steel cable with the CFRP cable can reduce the large vibrations of the inclined cable (see Fig. 13).

|
| Fig. 12 Frequency-response curves of the steel cable |
|
|
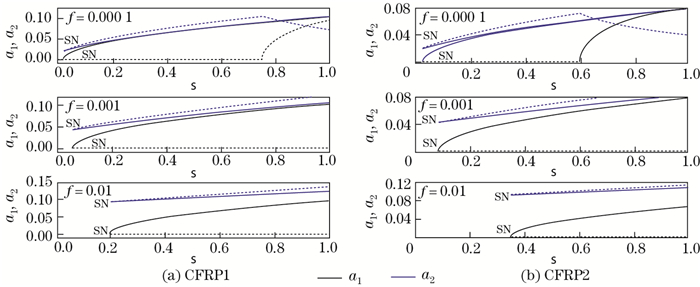
|
| Fig. 13 Frequency-response curves of the CFRP cables (color online) |
|
|
Figure 14 shows the force-response curves of cables with different materials and excitation frequencies when the excitation is applied to the out-of-plane mode. The comparison of Figs. 14 and 11 shows that they are almost similar. The main difference is that there is only one Hopf bifurcation for every case in Fig. 14, which means that the dynamic behavior becomes simpler when excitation is applied to the out-of-plane mode.
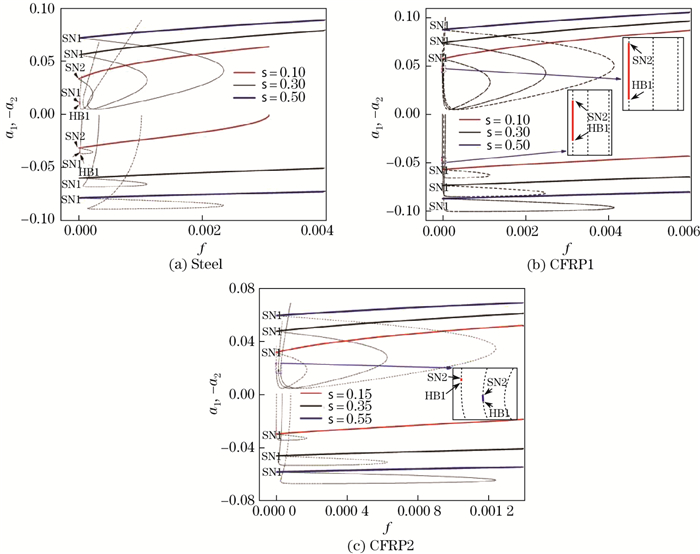
|
| Fig. 14 Force-response curves of cables with different materials |
|
|
In order to model the harmonic excitation generated by wind, the excitation loads applied to both in-plane and out-of-plane modes are assumed to have the same frequency, i.e., Ω1=Ω2, and k is used to adjust the relative magnitude in the two different planes of the cable, i.e., f2=kf1. The nondimensional load applied to the in-plane mode is twice that of the out-of-plane mode as k=0.5, and vice versa as k=2.
Figure 15 shows the frequency-response curves of the steel cable with different forces as Ω1=Ω2. Although the frequency-response curves still have the characteristic of hard spring, there exists a stable branch σ < 0. In other words, the resonant frequency range expands to almost twice that of the excitation applied to each plane separately. From Fig. 15(a), it can be seen that the primary resonant frequency range will expand further when the excitation amplitude increases. Two saddle node bifurcations are observed in the primary resonant frequency range. By comparing Figs. 15, 10(a), and Figs. 12, it can be concluded that the dynamic behaviors of the steel cable become increasingly complex when excitation is applied to the in-plane, out-of-plane, and both in-plane and out-of-plane modes. Two branches of the equilibrium solutions, one is stable and the other one is unstable, emerge from the saddle node bifurcation (SN1) at σ=0.115 2. Therefore, there exist two almost identical stable branches of equilibrium solutions when σ≥0.015 2, as shown in Fig. 15(a). Another two branches of equilibrium solutions emerge from the other saddle node bifurcation (SN2) at σ=0.112 6. Therefore, there are five branches of equilibrium solutions when σ≥0.112 6, which is different from the dynamic behavior of the system as excitation is applied to each single plane. In addition, the response amplitudes a1 and -a2 of the in-plane and out-of-plane modes are not symmetrical even if k=1, as shown in Fig. 15(b). The response amplitude a1 of the in-plane mode is slightly larger than the amplitude a2 of the out-of-plane mode, even if k=2, which could be attributed to the in-plane initial geometric configuration of the steel cable.

|
| Fig. 15 Frequency-response curves of the steel cable with different forces |
|
|
Figure 16 shows the force-response curves of the steel cable with different constant detuning parameters σ when Ω1=Ω2. It is seen that there exists only one stable branch of equilibrium when σ < 0, as shown by the right graph in Fig. 16(a). This further confirms the results shown in Fig. 15. As seen in the left graph in Fig. 16(a), when the excitation amplitude f decreases from 0.01, the stable coupled equilibrium solutions, i.e., a1 and -a2, decrease and become unstable through the saddle node bifurcation at SN4. They may also jump to other stable branches through the saddle node bifurcation at SN1, and then end at f=0.005. Moreover, they may jump through the saddle node bifurcation at SN3, and become unstable through the Hopf bifurcation at HB2. Then, the unstable coupled solutions regain their stability through another Hopf bifurcation at HB1. Lastly, they decrease rapidly and end through the saddle node bifurcation at SN2.

|
| Fig. 16 Force-response curves of the steel cable with different forces |
|
|
As we know, there exist three stable branches of equilibrium solutions when σ≥0.112 6. Another stable branch is given in Fig. 16(b) when

|
It is seen that the force-response curves form a closed curve, and consist of one stable branch and some unstable branches of equilibrium solutions within a certain excitation force range. As the excitation amplitude f decreases from 0.006 when σ=0.15, the stable coupled steady-state solutions, i.e., a1 and -a2, start through a saddle node bifurcation at SN3, and then decrease and end through another saddle node bifurcation at SN1. They may also jump to other stable branches through the saddle node bifurcation at SN2, and become unstable through the Hopf bifurcation at HB. From Fig. 16(c), it is noted that the excitation force range for one of the stable branches arising at SN1 shifts to the left significantly, which means that the increase in the excitation force applied to the out-of-plane mode can narrow the excitation force range for multiple equilibrium solutions.
The cable materials CFRP1 and CFRP2 are considered to explore the effects of new materials on the nonlinear dynamics. Figure 17 shows the force-response curves of the CFRP1 cable when σ=0.75 and k=0.5. Compared with Fig. 16(a), there are three stable branches of equilibrium solutions within a small excitation force range, and the dynamics of the CFRP1 cable is similar to that of the steel cable system. However, the response amplitude and excitation force range for the primary resonance are reduced when the CFRP1 cable is used to replace the steel cable as k = 2, as shown in Fig. 18.

|
| Fig. 17 Force-response curves of the CFRP1 cable, where k = 0.5 (color online) |
|
|

|
| Fig. 18 Force-response curves of the CFRP1 cable, where σ = 0.25 (color online) |
|
|
The nonlinear dynamic behaviors of the CFRP2 cable are shown in Figs. 19 and 20. An interesting phenomenon for the largest stable branches of equilibrium solutions is observed, as shown in Fig. 19. When the excitation force increases from zero and k=1, the response amplitude a2 of the in-plane mode increases while that of the out-of-plane mode decreases. Besides, when the excitation force increases from zero and k=2, the response amplitude a2 of the out-of-plane mode increases, while the response amplitude a1 of the in-plane mode decreases. In both the equilibrium solutions, a1 and a2 increase when k = 1. These mean that the energy transmission through the one-to-one internal resonance is considerable when the internal resonance is excited and the ratio of energy transmission decreases with the increase in the excitation force. Therefore, the energy transmission between the lowest in-plane and out-of-plane modes through the internal resonance is nonlinear because of the nonlinear couple. Moreover, smaller stable branches become unstable when k = 2, which is detrimental in practice because the unstable solution will converge to the large stable one.

|
| Fig. 19 Force-response curves of the CFRP cable (CFRP2, σ = 0.75) (color online) |
|
|

|
| Fig. 20 Frequency-response curves of the CFRP cable with different forces (CFRP2, f = 0.001) (color online) |
|
|
Figure 20 shows the frequency-response curves of the CFRP2 cable with different forces as f=0.001. The nonlinear dynamic behavior is similar to that of the steel cable because of the similar frequency-response curves and identical bifurcations while the detuning parameter σ shifts to the right. This means that the primary resonant frequency range expands when the external excitation is applied to the out-of-plane mode of the CFRP2 cable, which is more obvious than that of the steel cable. It is important to note that the response amplitudes of both planes decrease significantly when the CFRP2 cable is used to reduce the vibration of the cable, as shown in Fig. 21.

|
| Fig. 21 Frequency-response curves of cables with different material (k = 2 and f = 0.000 1) (color online) |
|
|
The mechanical and mathematical mode-reduced model for the analysis of 3D vibration problems of the inclined CFRP cable is established. The eigenvalues for the free vibration of the CFRP cable are solved by the analytical method. Then, the nonlinear dynamic behavior of the cable with different materials under one-to-one internal resonance between both the lowest in-plane and out-of-plane modes are investigated by the MSM when the system is subject to the in-plane and out-of-plane harmonic excitations independently and simultaneously. The parametric analyses of both free linear vibration and forced nonlinear dynamics are conducted. Some meaningful and novel phenomena and suggestions are drawn as follows by a systemic dynamic analysis of the midspan of the cable:
(ⅰ) The temperature, the elasto-geometric parameter, and the ratio of Young's modulus to the shear modulus have significant effects on the natural frequencies of the in-plane mode of the inclined CFRP cable. The bending stiffness has a significant effect on the natural frequencies of both the in-plane and the out-of-plane modes.
(ⅱ) The axial Young's modulus plays an important role not only in increasing the cable strength but also in adjusting the natural frequencies of the in-plane and out-of-plane modes, which could be utilized to control the large vibration of the inclined cable in cable-stayed bridges.
(ⅲ) The CPMS is defined, which is the transition of the mode shape from having no internal node to having internal nodes or vice versa. Furthermore, it is observed that the CPMS is not coincident with the CPF.
(ⅳ) Another interesting observation is that the crossover between the two frequency spectra of the fifth-order symmetrical and antisymmetrical modes occurs twice with the increase in the ratio of Young's modulus to the shear modulus.
(ⅴ) The shifting and expanding phenomena in the frequency range for the primary resonance with increasing the excitation amplitude are observed, regardless of whether the load is added in-plane, out-of-plane, or both. This means that the bigger the excitation amplitude is, the larger the resonant frequency range is.
(ⅵ) The CFRP cable can reduce the large vibration compared with the steel cable because it makes the occurrence of the primary resonance more difficult by shifting the threshold frequency, triggering the large vibration far away from the natural frequency, and reducing the excitation force range inducing external primary and internal resonances.
(ⅶ) The dynamic behavior of the system under the in-plane excitation is similar to that under the out-of-plane excitation. The single modal response could be excited when the excitation is applied to the out-of-plane mode. However, more complex dynamic behaviors are observed when the system is excited on both planes, especially when the resonant frequency range has expanded twice.
(ⅷ) The response amplitudes of both modes of the system are not symmetrical, even if the same excitation is applied to both the in-plane and the out-of-plane modes because of the in-plane static configuration.
(ⅸ) The energy transmission through one-to-one internal resonance is considerable when the internal resonance is triggered. Then, the ratio of energy transmission decreases with increasing the excitation force. Therefore, the energy transmission between the in-plane mode and the out-of-plane mode through the internal resonance is nonlinear because of their nonlinear coupling.
AcknowledgementsInteresting comments by the reviewers are gratefully acknowledged.
| [1] |
IRVINE, H. M Cable Structures, MIT Press, Cambridge (1981)
|
| [2] |
TRIANTAFYLLOU, M. S. Dynamics of cables, towing cables and mooring systems. Shock and Vibration Digest, 23, 3-8 (1991) |
| [3] |
STAROSSEK, U. Cable dynamics:a review.. Structural Engineering International, 4, 171-176 (1994) doi:10.2749/101686694780601908 |
| [4] |
REGA, G. Nonlinear vibrations of suspended cables, part I:modeling and analysis. Applied Mechanics Reviews, 57, 443-478 (2004) doi:10.1115/1.1777224 |
| [5] |
REGA, G. Nonlinear vibrations of suspended cables, part Ⅱ:deterministic phenomena. Applied Mechanics Reviews, 57, 479-514 (2004) doi:10.1115/1.1777225 |
| [6] |
WEI, M. H., XIAO, Y. Q., and LIU, H. T. Bifurcation and chaos of a cable-beam coupled system under simultaneous internal and external resonances. Nonlinear Dynamics, 67, 1969-1984 (2012) doi:10.1007/s11071-011-0122-3 |
| [7] |
LUONGO, A. and ZULLI, D. Dynamic instability of inclined cables under combined wind flow and support motion. Nonlinear Dynamics, 67, 71-87 (2012) doi:10.1007/s11071-011-9958-9 |
| [8] |
GHOLIPOUR, A., FAROKHI, H., and GHAYESH, M. H. In-plane and out-of-plane nonlinear size-dependent dynamics of microplates. Nonlinear Dynamics, 79, 1771-1785 (2015) doi:10.1007/s11071-014-1773-7 |
| [9] |
GHAYESH, M. H., FAROKHI, H., and AMABILI, M. In-plane and out-of-plane motion characteristics of microbeams with modal interactions. Composites Part B:Engineering, 60, 423-439 (2014) doi:10.1016/j.compositesb.2013.12.074 |
| [10] |
GHAYESH, M. H. and FAROKHI, H. Nonlinear dynamics of microplates. International Journal of Engineering Science, 86, 60-73 (2015) doi:10.1016/j.ijengsci.2014.10.004 |
| [11] |
MEI, K., SUN, S., JIN, G., and SUN, Y. Static and dynamic mechanical properties of long-span cable-stayed bridges using CFRP cables. Advances in Civil Engineering, 2017, 1-11 (2017) |
| [12] |
LIU, Y. Carbon fiber reinforced polymer (CFRP) cables for orthogonally loaded cable structures:advantages and feasibility. Structural Engineering International, 26, 179-181 (2016) doi:10.1080/10168664.2016.11985561 |
| [13] |
KREMMIDAS, S. C. Improving Bridge Stay Cable Performance under Static and Dynamic Loads, Ph. D. dissertation, University of California, San Diego (2004)
|
| [14] |
KAO, C. S., KOU, C. H., and XIE, X. Static instability analysis of long-span cable-stayed bridges with carbon fiber composite cable under wind load (in Chinese) (in Chinese). Tamkang Journal of Science and Engineering, 9, 89-95 (2006) |
| [15] |
KOU, C. H., XIE, X., GAO, J. S., and HUANG, J. Y. Static behavior of long-span cable-stayed bridges using carbon fiber composite cable (in Chinese) (in Chinese). Journal of Zhejiang University, 39, 137-142 (2005) |
| [16] |
FAN, Z., JIANG, Y., ZHANG, S., and CHEN, X. Experimental research on vibration fatigue of CFRP and its influence factors based on vibration testing. Shock and Vibration, 2017, 1-18 (2017) |
| [17] |
XIE, X., LI, X., and SHEN, Y. Static and dynamic characteristics of a long-span cable-stayed bridge with CFRP cables. Materials, 7, 4854-4877 (2014) doi:10.3390/ma7064854 |
| [18] |
XIE, X., GAO, J. S., KOU, C. H., and HUANG, J. Y. Structural dynamic behavior of longspan cable-stayed bridges using carbon fiber composite cable (in Chinese) (in Chinese). Journal of Zhejiang University, 39, 728-733 (2005) |
| [19] |
KANG, H. J., ZHU, H. P., ZHAO, Y. Y., and YI, Z. P. In-plane non-linear dynamics of the stay cables. Nonlinear Dynamics, 73, 1385-1398 (2013) doi:10.1007/s11071-013-0871-2 |
| [20] |
KANG, H. J., ZHAO, Y. Y., and ZHU, H. P. Linear and nonlinear dynamics of suspended cable considering bending stiffness. Journal of Vibration and Control, 21, 1487-1505 (2015) doi:10.1177/1077546313499390 |
| [21] |
LEPIDI, M. and GATTULLI, V. Static and dynamic response of elastic suspended cables with thermal effects. Int. Journal of Solids and Structure, 49, 1103-1116 (2012) doi:10.1016/j.ijsolstr.2012.01.008 |
| [22] |
LUONGO, A., REGA, G., and VESTRONI, F. Monofrequent oscillations of a non-linear model of a suspended cable. Journal of Sound and Vibration, 82, 247-259 (1982) doi:10.1016/0022-460X(82)90533-8 |
| [23] |
RICCIARDI, G. and SAITTA, F. A continuous vibration analysis model for cables with sag and bending stiffness. Engineering Structures, 30, 1459-1472 (2008) doi:10.1016/j.engstruct.2007.08.008 |
| [24] |
SOUSA, R. A., SOUZA, R. M., FIGUEIREDO, F. P., CAMBIER, P., OLIVEIRA, A. C., and SOUZA, R. M. The influence of bending and shear stiffness and rotational inertiain vibrations of cables:an analytical approach. Engineering Structures, 33, 689-695 (2011) doi:10.1016/j.engstruct.2010.11.026 |
| [25] |
CEBALLOS, M. A. and PRATO, C. A. Determination of the axial force on stay cables accounting for their bending stiffness and rotational end restraints by free vibration tests. Journal of Sound and Vibration, 317, 127-141 (2008) doi:10.1016/j.jsv.2008.02.048 |
| [26] |
NAYFEH, A. H. and MOOK, D. T Nonlinear Oscillations, Wiley, New York (1979)
|
| [27] |
DING, H., HUANG, L., MAO, X., and CHEN, L. Primary resonance of traveling viscoelastic beam under internal resonance. Applied Mathematics and Mechanics (English Edition), 38(1), 1-14(2017) https://doi.org/10.1007/s10483-016-2152-6
|
| [28] |
GUO, T., KANG, H., WANG, L., and ZHAO, Y Triad mode resonant interactions in suspended cables. Science China:Physics, Mechanics and Astronomy, 59, 1-14 (2016) doi:10.1007/s11425-015-5107-0 |
 2019, Vol. 40
2019, Vol. 40


