Shanghai University
Article Information
- FARAJI-OSKOUIE M., NOROUZZADEH A., ANSARI R., ROUHI H.
- Bending of small-scale Timoshenko beams based on the integral/differential nonlocal-micropolar elasticity theory: a finite element approach
- Applied Mathematics and Mechanics (English Edition), 2019, 40(6): 767-782.
- http://dx.doi.org/10.1007/s10483-019-2491-9
Article History
- Received Sep. 17, 2018
- Revised Jan. 3, 2019
2. Department of Engineering Science, Faculty of Technology and Engineering, University of Guilan, Rudsar-Vajargah 44891-63157, Iran
Generalized continuum theories are widely used to address the problems of small-scale structures[1-7]. They are also used for analyzing heterogeneous materials, lattices, foams, polycrystals, cellular solids, liquid crystals, and masonries[8-11]. One can categorize these theories into three classes: 3M, strain gradient, and nonlocal elasticity. The micromorphic, microstretch, and micropolar (abbreviated as 3M) are the high-order models proposed for capturing the size-dependency as well as the inhomogeneity of materials[12]. As the most popular one, the micropolar theory is introduced in the following. Also, the recent contributions on the most complete one, i.e., the micromorphic theory, can be found in Refs. [13]-[16]. The strain gradient theories (SGTs) are formulated by taking the gradients of strain field into account and defining the non-classical stress and strain measures. Depending on the number of material length-scale parameters, the first and second SGTs, the couple stress theory (CST), the modified couple stress theory (MCST), and the modified strain gradient theory (MSGT) were developed[17-21]. Among various attempts in this area[22-28], one can mention the work of Reddy[25], in which the geometrically nonlinear bending, vibration, and buckling of functionally graded beams were investigated by the one-parameter modified couple stress model of the Euler-Bernoulli and Timoshenko beams. Moreover, the nonlocal continuum theory is reviewed in the following.
The micropolar theory is a generalized continuum theory that can be efficiently used in the analysis of materials taking the microstructure effect into account. The concept of this theory was first introduced by Cosserat brothers in 1909[29]. However, the main development of micropolar continuum mechanics dated back to the 1960s with the works of Eringen and Suhubi[30], Suhubi and Eringen[31], and Eringen[32-34]. Based on the micropolar theory, the rotational degrees of freedom (DOFs) of material particles were taken into account as independent variables. At each material point of micropolar continua, a microstructure or an infinitesimal rigid body was considered which can rotate independently from the neighbouring medium[35-36]. As a result, each material particle has three rotational DOFs in addition to three translational ones. More details on the concepts of micropolar continuum mechanics can be found in Refs. [12] and [37]-[43].
The nonlocal theory is another generalized continuum theory which can be applied to the problems of small-scale structures. In a nonlocal model, the stress tensor at a point depends on the strain tensor at all points of the body. This theory was first developed by Kröner[44], Krumhansl[45], and Kunin[46]. Moreover, its first formal introduction is associated with the papers of Eringen[47] and Eringen and Edelen[48].
Eringen's nonlocal theory was firstly formulated in the integral form, and kernel functions were employed in order to take the nonlocal effects into consideration. Then, Eringen[49] proposed the differential version of his theory. The differential nonlocal theory has been broadly utilized by many researchers up to now, e.g., Refs. [50]-[57]. A literature review reveals that there are two nonlocal differential forms named as the weakened and enhanced models which respectively predict the softening and stiffening behaviors with the increase in the nonlocal parameter. Li[53] compared these models and showed that according to different surface effects in the discrete atomic layers of the carbon nanotube, both models were valid.
However, using the differential form in some problems may lead to paradoxical results, and recourse must be made to the original (integral) form of the nonlocal theory. A famous paradox occurs in the bending analysis of cantilevers. As a general rule, increasing the nonlocal parameter has softening influence on the response of structure. Nonetheless, the deformation of cantilevers under bending decreases by increasing the nonlocal parameter (i.e., the hardening influence). For that reason, as well as some other paradoxes, considering the nonlocal effects by the integral nonlocal theory has become popular in recent years[58-69]. For instance, Challamel and Wang[58] analyzed the bending characteristics of nonlocal rods via a combination of the local and non-local curvatures inserted in the integral constitutive equations. Also, Norouzzadeh and Ansari[64] developed a finite element (FE) solution procedure for the integral nonlocal elasticity and resolved the paradoxes of differential model of Timoshenko nonlocal beams.
In this article, an attempt is made at predicting the static bending behavior of small-scale beams taking the rotational DOFs of material particles and nonlocal effects into account simultaneously. To this end, Eringen's micropolar theory[30-34] is combined with his nonlocal theory. According to the integral (original)[47-48] and differential[49] versions of the nonlocal theory, an integral nonlocal-micropolar (INM) model and a differential nonlocal-micropolar (DNM) model are developed. To the authors' best knowledge, this is for the first time that a hybrid generalized continuum theory is proposed to capture the nonlocal and microstructure effects on the mechanical behavior of small-scale structures. The governing equations are obtained in the context of first-order shear deformation beam theory and using Hamilton's principle. The tensor form of equations is replaced by a novel matrix-vector format. Based on this feature, the formulation can be readily used in the coding process of numerical methods. An FE method is then proposed for the solution to the governing equations. Finally, the impacts of nonlocal parameter-to-length and thickness-to-characteristic bending length ratios on the deformation of Timoshenko beams subject to various end conditions are explored.
2 FormulationFigure 1 shows the beam under consideration. A Cartesian coordinate system is used in which the x-, y-, and z-axes denote the longitudinal, vertical, and transverse directions, respectively. The geometry of the beam is identified with the length L, the width b, and the height h.
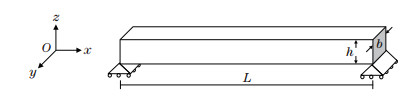
|
| Fig. 1 Schematic view of the considered beam |
|
|
Based upon Eringen's micropolar theory, one has the components of the stress σij and the couple stress mij of a typical one-dimensional structure x, as the beam shown in Fig. 1, as follows:
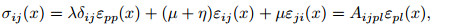
|
(1) |
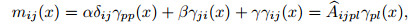
|
(2) |
where δij is the Kronecker delta symbol. λ and μ denote the classical Lamé constants, and η, α, β, and γ are the additional elastic parameters from the micropolar theory. Accordingly, the fourth-order elasticity tensors can be introduced in the following way:
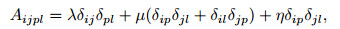
|
(3) |
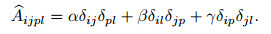
|
(4) |
Also, εij and γij represent the so-called micropolar strain and wryness tensors, respectively, which can be defined as
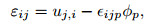
|
(5) |
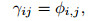
|
(6) |
where ϵijp shows the permutation symbol. Moreover, the displacement ui and the micro-rotation ϕi contain six DOFs comprising three translational and three rotational DOFs.
2.1 INM theoryFor capturing the nonlocal effects of the stress-strain relationship at small scales, the given stress-strain equations are extended using the integral version of nonlocal theory as
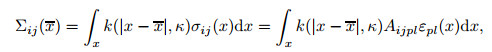
|
(7) |
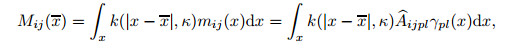
|
(8) |
in which Σij and Mij are the corresponding nonlocal stress tensors. Also, κ denotes the nonlocal parameter.
Now, the macro-displacement field is considered based on the Timoshenko beam theory as
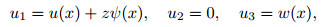
|
(9) |
where u(x), w(x), and ψ(x) stand for the axial and lateral deflections and the rotation angle of the cross section according to the vertical direction, respectively. Taking the transverse shear deformation and rotary inertia into account, the Timoshenko theory can appropriately model both the thick and thin beam-type structures.
Also, considering Fig. 1, it should be noted that a beam element can only possess the micro-rotation component in the y-direction, i.e.,
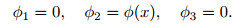
|
(10) |
Now, the following relations corresponding to non-zero values of displacement components are defined:
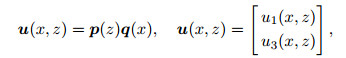
|
(11) |
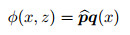
|
(12) |
with the coefficient matrices p and 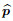
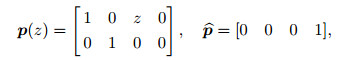
|
(13) |
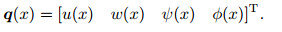
|
(14) |
Here, with respect to Eqs. (5) and (6), the appropriate matrix-vector representation can be considered to determine the equivalent vector forms of strain tensors as
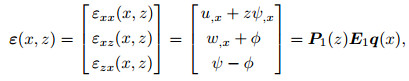
|
(15) |
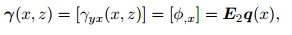
|
(16) |
where the coefficient matrix P1 and the differentiation operators E1 and E2 are

|
(17) |
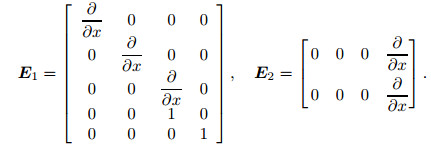
|
(18) |
From Eqs. (7) and (8), one has
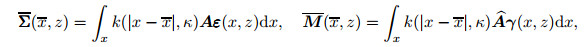
|
(19) |
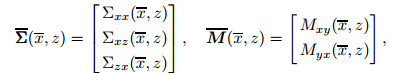
|
(20) |
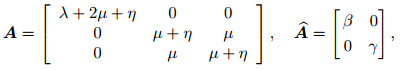
|
(21) |
where A and  are the matrix representations of the elasticity tensors defined in Eqs. (3) and (4), respectively. Hamilton's principle is used to derive the equations of motion. This principle is formulated as
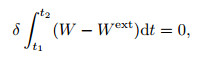
|
(22) |
in which W and Wext exhibit the total strain energy and the external work, respectively. δ is the symbol of variation, and t stands for the time. In this manner, the strain energy of beam with the surface area A can be written as
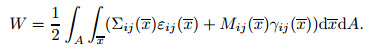
|
(23) |
The variation of strain energy in the matrix-vector format is thus obtained as
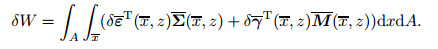
|
(24) |
According to Eqs. (15) and (16), one has
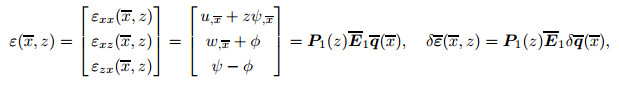
|
(25) |
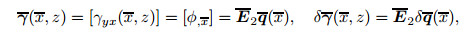
|
(26) |
where
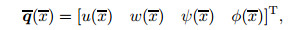
|
(27) |
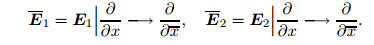
|
(28) |
At this stage, via considering
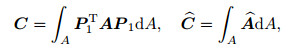
|
(29) |
one has
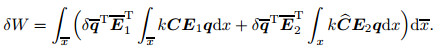
|
(30) |
Consider that the beam is subject to the distributed transverse load Fw. The applied work and its variation are determined in the following manner:
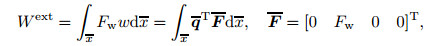
|
(31) |
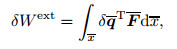
|
(32) |
where F shows the load vector.
2.2 DNM theoryUsing the differential model of Eringen's nonlocal continuum, the counterpart of constitutive relations in Eqs. (7) and (8) is determined as
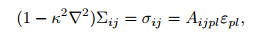
|
(33) |
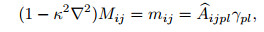
|
(34) |
where the Laplacian operator in the one-dimensional analysis is given as 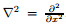
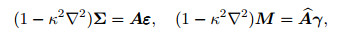
|
(35) |
in which
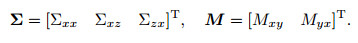
|
(36) |
Also, from Subsection 2.1, one can find the vectors ε and γ and matrices A and  in Eqs. (15), (16), and (21), respectively.
Here, the strain energy of structure is given by
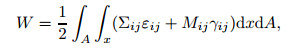
|
(37) |
or
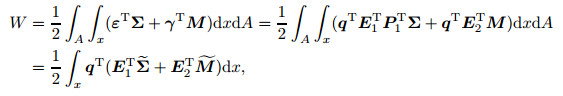
|
(38) |
in which the resultant vectors 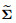
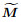
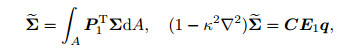
|
(39) |
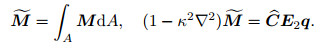
|
(40) |
C and Ĉ have been defined in Eq. (29). Hence, in the differential model, δ W is achieved as follows:
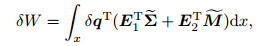
|
(41) |
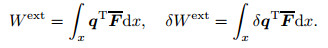
|
(42) |
Using Hamilton's principle leads to
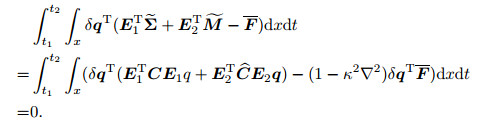
|
(43) |
Therefore, the variations of equivalent strain energy and external work are obtained, respectively, as
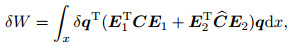
|
(44) |
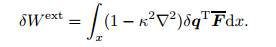
|
(45) |
An FE method is proposed for the solution procedure. For the INM model, it is required to utilize a novel solution procedure, i.e., at any assumed point of x, the assemblage of stress vectors must be done in the whole domain of x. Next, the outer assemblage in the x domain leads to the total stiffness matrix. The conventional FE analysis can also be implemented in the differential model of present formulation.
3.1 INM theoryIn an element, interpolation of the displacement components is done using suitable shape functions. It is assumed that the associated local coordinates of the x and x domains are shown as ξ and ξ, respectively. Considering the shape function of ith node as Ni, one can write
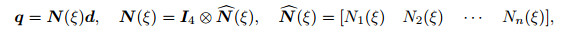
|
(46) |
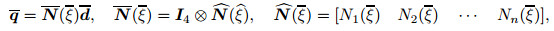
|
(47) |
where d and d denote the nodal variables in the ξ- and ξ-coordinates, respectively. Furthermore, ⊗ denotes the Kronecker delta product, Ip is the p-by-p identity matrix, and n is the number of nodes in the element.
Therefore, the strain vectors and their variation are determined in a typical element as
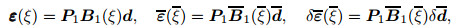
|
(48) |
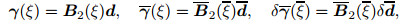
|
(49) |
where
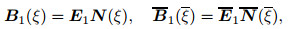
|
(50) |
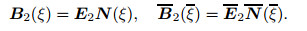
|
(51) |
Here, to obtain the stress vectors, one can define the following relations:
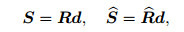
|
(52) |
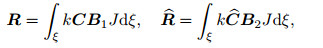
|
(53) |
where J stands for the determinant of Jacobian transformation matrix. After completing the inner assemblage process in the ξ-coordinate, the total matrices of S, Ŝ, R, and 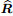
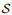
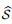
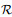
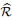
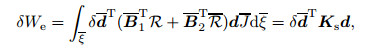
|
(54) |
where J is the counterpart of J in the ξ-coordinate. The scant stiffness matrix of the element Ks is given by
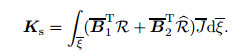
|
(55) |
In addition, the external work applied on the element can be expressed as
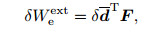
|
(56) |
in which F stands for the force vector of element,
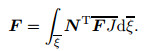
|
(57) |
By assembling the stiffness and force vectors, the total matrices and vectors of 
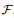
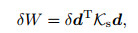
|
(58) |
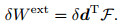
|
(59) |
Finally, Hamilton's principle reveals that
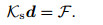
|
(60) |
As seen in the foregoing solution procedure, an assemblage in the whole beam domain is needed to derive the stress vectors in each reference point. Then, the total stiffness matrix is achieved by assembling the element matrices in the reference local coordinate. Such a method is deduced from the integral nature of constitutive equations and accordingly leads to higher computational cost rather than the standard FE analysis.
3.2 DNM theoryBy adopting the conventional FE analysis, one can find the solution to the problem based on the combination of differential model of nonlocal elasticity and the micropolar theory. Thus,
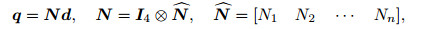
|
(61) |
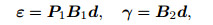
|
(62) |

|
(63) |
By inserting the presented interpolation into the equivalent energy terms in Eqs. (44) and (45), the variations of strain energy and external work are written as
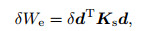
|
(64) |
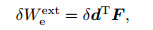
|
(65) |
where the stiffness matrix and force vectors of the element are
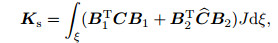
|
(66) |
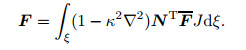
|
(67) |
Determining the total matrices and vectors leads to the equilibrium equations as Eq. (60).
4 Results and discussionTo generate the numerical results for the bending analysis of beams, the material properties (polyurethane foam) and geometrical parameters are considered as[70]
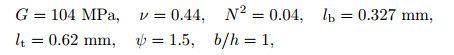
|
where G, ν, N, lb, lt, and ψ are the shear modulus, Poisson's ratio, the coupling number, the characteristic bending length, the characteristic torsion length, and the polar ratio, respectively. Considering the following formulae:
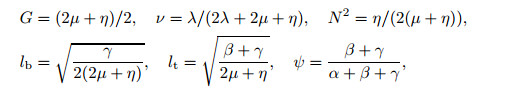
|
one has
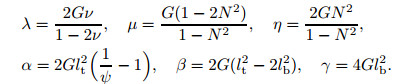
|
Note that the micropolar theory can be reduced to the classical theory through setting N, lb, and lt equal to zero.
In the nonlocal theory, the following standard kernel function is used:
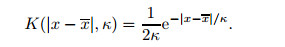
|
Also, the nondimensional deflection is defined as
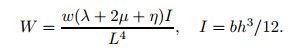
|
In the following, parametric studies are presented on the bending of C-C, C-SS, SS-SS, and C-F beams under a uniform distributed load, where clamped, simply-supported, and free ends are abbreviated to C, SS, and F, respectively.
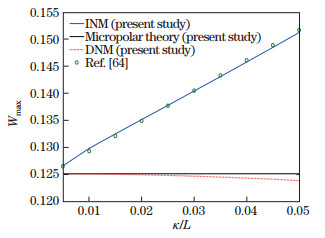
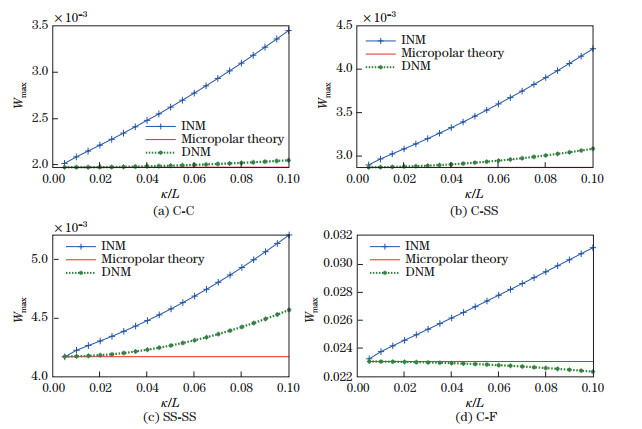
In Fig. 2, the maximum nondimensional deflection Wmax is plotted versus κ/L (the nondimensional nonlocal parameter) for a cantilever considering h/lb (the nondimensional length scale parameter) equal to 100. Defining the nondimensional nonlocal parameter as 0≤ κ/L≤1 allows us to directly examine the nonlocality effects by the proportional neighbourhood distances. The results are obtained using three models including the INM, DNM, and pure micropolar. Moreover, a comparison is made between the results of the present INM model and those of the integral nonlocal model reported by Norouzzadeh and Ansari[64]. First, it is seen that the current predictions agree well with the results produced in Ref. [64], showing the validity of current approach. In addition, it is clearly observed that the developed integral model is capable of resolving the paradox of C-F beam. In other words, the deflection of cantilever decreases by increasing the nondimensional nonlocal parameter using the differential model (the hardening effect), whereas consistent results are obtained based on the integral formulation (the softening effect). It is also worth mentioning that, since the micropolar effects are negligible (h/lb=100) in this case study, the present micropolar and DNM beam models are, respectively, in excellent agreement with the classical and differential nonlocal elasticity theories in Ref. [64].
|
Fig. 2 Variations of the maximum nondimensional deflection of C-F beam with the nonlocal parameters 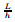 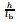 |
|
|
In Fig. 3, the nonlocal effects on the bending behavior of beams under C-C, C-SS, SS-SS, and C-F end conditions are illustrated for a range of length-to-thickness ratio L/h. The maximum deflections are computed based on the INM, DNM, and micropolar theories. Various nondimensional nonlocal parameters are considered, and it is assumed that h/lb=5. The length-to-thickness ratio is varied from 10 to 30. As expected, the deflection of beams decreases when L/h goes higher. One can find that for all boundary conditions except C-F, the deflections obtained based on the micropolar model are lower than those obtained by the other models. Moreover, increasing the nondimensional nonlocal parameter leads to increasing Wmax. In the case of C-F beam, the results of the DNM are lower than those of the micropolar model, and the increase in κ/L has hardening influence on the bending response. Employing the INM can successfully resolve the paradox and consistent softening behavior. Another finding is that larger deflections are obtained using the integral formulation as compared with the differential formulation. Accordingly, although the trend of changes is similar in both nonlocal models of non-cantilever beams, the values of maximum deformation are different between the original and differential forms.
|
Fig. 3 Variations of the maximum nondimensional deflection of beams subject to different boundary conditions with the length-to-thickness ratio 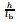 |
|
|
Similar to Fig. 2, the variations of Wmax with κ/L are indicated in Fig. 4 for beams under different boundary conditions considering the significant impacts of micro-rotational DOFs with h/lb=1. Again, it is seen that using the differential model to predict the bending response of C-F beam leads to paradoxical results, while its integral counterpart can consistently capture the nonlocal effect. Moreover, it is seen that the nonlocality captured by the integral model is more pronounced than that captured by the differential model. Therefore, one can observe that the inconsistency of differential nonlocal formulation still exists even when the microstructure effects are dominant.
|
Fig. 4 Variations of the maximum nondimensional deflection of beams subject to different boundary conditions with the nonlocal parameters   |
|
|
Finally, the simultaneous effects of κ/L and h/lb on the bending behavior of beams under various end conditions are shown in Fig. 5. The results of this figure are obtained on the basis of the INM and classical theories. It is observed that increasing κ/L and h/lb leads to the increase in the deflection. Thus, in addition to the softening responses of the nonlocal elasticity, the hardening behavior of the micropolar theory is observed in this figure. It is interesting to note that one can find specific values of these parameters at which the results of the nonlocal-micropolar theory become identical to those of the classical theory (the micropolar and nonlocal effects cancel each other out). From Figs. 5(a)-5(d), it is found that these values are highly dependent on the beam boundary conditions. Such a phenomenon was also reported in the nonlocal strain gradient models, namely, corresponding to certain pairs of nonlocal and small scale parameters, the classical and generalized continuum mechanics predicted the same responses[71-74].
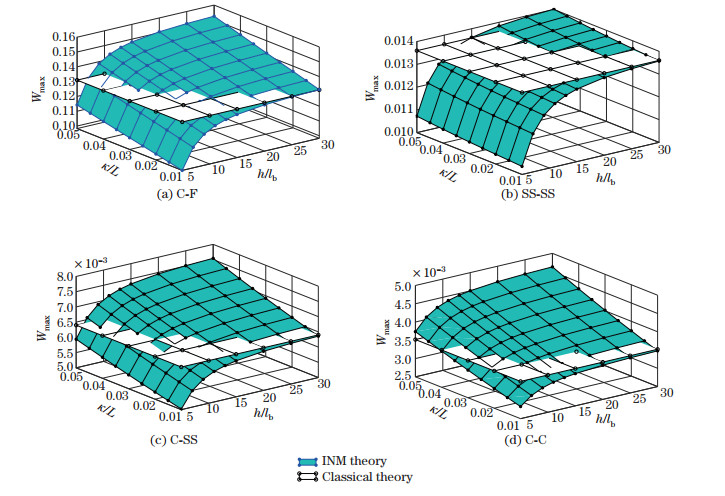
|
| Fig. 5 Simultaneous effects of nonlocal and length scale parameters on the bending of beams subject to C-F, SS-SS, C-SS, and C-C boundary conditions (color online) |
|
|
Within a new continuum framework, the static bending problem of small-scale Timoshenko beams is addressed through a numerical approach. The size effects are considered by combining the micropolar theory with the nonlocal elasticity. The formulation of the paper is derived for two cases. In the first one, the integral form of nonlocal elasticity theory is considered, whereas the differential nonlocal model is used in the second one. Based on a vector-matrix formulation and an FE analysis, the maximum deflections of beams with SS-SS, C-C, C-SS, and C-F boundary conditions are calculated considering nonlocal and microstructure effects. Selected numerical results are presented to investigate the influence of nonlocal/length scale parameters on the bending behavior of beams based on different models. The important findings can be summarized as follows.
(ⅰ) The developed hybrid model can be efficiently employed to predict the bending behavior of beam-type small-scale structures considering simultaneous microstructure and nonlocal effects. The proposed numerical approach is also found to be capable of solving the problem accurately.
(ⅱ) The paradox related to the C-F beam is resolved using the present integral model.
(ⅲ) The nonlocal effect captured by the integral model is more prominent than that in the differential model.
(ⅳ) Increasing both the nondimensional nonlocal and length scale parameters leads to an increase in the deflection which specifies the softening and hardening behaviors of the nonlocal and micropolar theories, respectively.
(ⅴ) Corresponding to certain nondimensional nonlocal and length scale parameters, the proposed high-order elasticity theory gives the same results as the classical continuum theory.
| [1] |
WANG, K. F., WANG, B. L., and KITAMURA, T. A review on the application of modified continuum models in modeling and simulation of nanostructures. Acta Mechanica Sininica, 32, 83-100 (2016) doi:10.1007/s10409-015-0508-4 |
| [2] |
ELTAHER, M. A., KHATER, M. E., and EMAM, S. A. A review on nonlocal elastic models for bending, buckling, vibrations, and wave propagation of nanoscale beams. Applied Mathematical Modelling, 40, 4109-4128 (2016) doi:10.1016/j.apm.2015.11.026 |
| [3] |
ANSARI, R., NOROUZZADEH, A., SHAKOURI, A. H., BAZDID-VAHDATI, M., and ROUHI, H. Finite element analysis of vibrating micro-beams and -plates using a three-dimensional micropolar element. Thin-Walled Structures, 124, 489-500 (2018) doi:10.1016/j.tws.2017.12.036 |
| [4] |
LI, C. A nonlocal analytical approach for torsion of cylindrical nanostructures and the existence of higher-order stress and geometric boundaries. Composite Structures, 118, 607-621 (2014) doi:10.1016/j.compstruct.2014.08.008 |
| [5] |
ŞMŞK, M. and REDDY, J.N. A unified higher order beam theory for buckling of a functionally graded microbeam embedded in elastic medium using modified couple stress theory. Composite Structures, 101, 47-58 (2013) doi:10.1016/j.compstruct.2013.01.017 |
| [6] |
ANSARI, R. and NOROUZZADEH, A. Nonlocal and surface effects on the buckling behavior of functionally graded nanoplates:an isogeometric analysis. Physica E, 84, 84-97 (2016) doi:10.1016/j.physe.2016.05.036 |
| [7] |
MA, H. M., GAO, X. L., and REDDY, J. N. A microstructure-dependent Timoshenko beam model based on a modified couple stress theory. Journal of Mechanics and Physics of Solids, 56(12), 3379-3391 (2008) doi:10.1016/j.jmps.2008.09.007 |
| [8] |
FATEMI, J., VAN KEULEN, F., and ONCK, P. Generalized continuum theories:application to stress analysis in bone. Meccanica, 37, 385-396 (2002) doi:10.1023/A:1020839805384 |
| [9] |
IVANOVA, E. A., KRIVTSOV, A. M., MOROZOV, N. F., and FIRSOVA, A. D. Description of crystal packing of particles with torque interaction. Mechanics of Solids, 38, 76-88 (2003) |
| [10] |
FOREST, S. and SAB, K. Cosserat overall modeling of heterogeneous materials. Mechanics Research Communications, 25, 449-454 (1998) doi:10.1016/S0093-6413(98)00059-7 |
| [11] |
YANG, J. F. C. and LAKES, R. S. Experimental study of micropolar and couple stress elasticity in compact bone in bending. Journal of Biomechanics, 15, 91-98 (1982) doi:10.1016/0021-9290(82)90040-9 |
| [12] |
ERINGEN, A. C. Microcontinuum Field Theory, Ⅰ. Foundations and Solids, Springer, Berlin (1999)
|
| [13] |
NEFF, P. and FOREST, S. A geometrically exact micromorphic model for elastic metallic foams accounting for affine microstructure:modelling, existence of minimizers, identification of moduli and computational results. Journal of Elasticity, 87(2-3), 239-276 (2007) doi:10.1007/s10659-007-9106-4 |
| [14] |
ISBUGA, V. and REGUEIRO, R. A. Three-dimensional finite element analysis of finite deformation micromorphic linear isotropic elasticity. International Journal of Engineering Science, 49(12), 1326-1336 (2011) doi:10.1016/j.ijengsci.2011.04.006 |
| [15] |
ANSARI, R., BAZDID-VAHDATI, M., SHAKOURI, A., NOROUZZADEH, A., and ROUHI, H. Micromorphic first-order shear deformable plate element. Meccanica, 51(8), 1797-1809 (2016) doi:10.1007/s11012-015-0325-7 |
| [16] |
ANSARI, R., BAZDID-VAHDATI, M., SHAKOURI, A. H., NOROUZZADEH, A., and ROUHI, H. Micromorphic prism element. Mathematics and Mechanics of Solids, 22(6), 1438-1461 (2017) doi:10.1177/1081286516637115 |
| [17] |
MINDLIN, R. D. Micro-structure in linear elasticity. Archive for Rational Mechanics and Analysis, 16(1), 51-78 (1964) doi:10.1007/BF00248490 |
| [18] |
MINDLIN, R. D. Second gradient of strain and surface-tension in linear elasticity. International Journal of Solids and Structures, 1(4), 417-438 (1965) doi:10.1016/0020-7683(65)90006-5 |
| [19] |
AIFANTIS, E. C. Fracture Scaling, Springer, Dordrecht, 299-314 (1999)
|
| [20] |
YANG, F. A. C. M., CHONG, A. C. M., LAM, D. C. C., and TONG, P. Couple stress based strain gradient theory for elasticity. International Journal of Solids and Structures, 39(10), 2731-2743 (2002) doi:10.1016/S0020-7683(02)00152-X |
| [21] |
LAM, D. C., YANG, F., CHONG, A. C. M., WANG, J., and TONG, P. Experiments and theory in strain gradient elasticity. Journal of Mechanics and Physics of Solids, 51(8), 1477-1508 (2003) doi:10.1016/S0022-5096(03)00053-X |
| [22] |
ROQUE, C. M. C., FIDALGO, D. S., FERREIRA, A. J. M., and REDDY, J. N. A study of a microstructure-dependent composite laminated Timoshenko beam using a modified couple stress theory and a meshless method. Composite Structures, 96, 532-537 (2013) doi:10.1016/j.compstruct.2012.09.011 |
| [23] |
REDDY, J. N. and KIM, J. A nonlinear modified couple stress-based third-order theory of functionally graded plates. Composite Structures, 94(3), 1128-1143 (2012) doi:10.1016/j.compstruct.2011.10.006 |
| [24] |
ANSARI, R., NOROUZZADEH, A., GHOLAMI, R., SHOJAEI, M. F., and HOSSEINZADEH, M. Size-dependent nonlinear vibration and instability of embedded fluid-conveying SWBNNTs in thermal environment. Physica E, 61, 148-157 (2014) doi:10.1016/j.physe.2014.04.004 |
| [25] |
REDDY, J. N. Microstructure-dependent couple stress theories of functionally graded beams. Journal of Mechanics and Physics of Solids, 59(11), 2382-2399 (2011) doi:10.1016/j.jmps.2011.06.008 |
| [26] |
ANSARI, R., GHOLAMI, R., NOROUZZADEH, A., and SAHMANI, S. Size-dependent vibration and instability of fluid-conveying functionally graded microshells based on the modified couple stress theory. Microfluidics Nanofluidics, 19(3), 509-522 (2015) doi:10.1007/s10404-015-1577-1 |
| [27] |
ANSARI, R., GHOLAMI, R., and NOROUZZADEH, A. Size-dependent thermo-mechanical vibration and instability of conveying fluid functionally graded nanoshells based on Mindlin's strain gradient theory. Thin-Walled Structures, 105, 172-184 (2016) doi:10.1016/j.tws.2016.04.009 |
| [28] |
KIM, J., ŻUR, K. K., and REDDY, J. N. Bending, free vibration, and buck·ling of modified couples stress-based functionally graded porous micro-plates. Composite Structures, 209, 879-888 (2019) doi:10.1016/j.compstruct.2018.11.023 |
| [29] |
COSSERAT, E. and COSSERAT, F. Théorie des Corps Déformables, Herman, Paris (1909)
|
| [30] |
ERINGEN, A.C. and SUHUBI, E. Nonlinear theory of simple micro-elastic solids-I. International Journal of Engineering Science, 2, 189-203 (1964) doi:10.1016/0020-7225(64)90004-7 |
| [31] |
SUHUBI, E. and ERINGEN, A. C. Nonlinear theory of micro-elastic solids-Ⅱ. International Journal of Engineering Science, 2, 389-404 (1964) doi:10.1016/0020-7225(64)90017-5 |
| [32] |
ERINGEN, A. C. Linear Theory of Micropolar Elasticity, Springer, New York (1965)
|
| [33] |
ERINGEN, A. C. Linear theory of micropolar viscoelasticity. International Journal of Engineering Science, 5, 191-204 (1967) doi:10.1016/0020-7225(67)90004-3 |
| [34] |
ERINGEN, A. C. Theory of micropolar plates. Zeitschrift für Angewandte Mathematik und Physik (ZAMP),, 18, 12-30 (1967) doi:10.1007/BF01593891 |
| [35] |
MINDLIN, R. D. Stress functions for a Cosserat continuum. International Journal of Solids and Structures, 1, 265-271 (1965) doi:10.1016/0020-7683(65)90033-8 |
| [36] |
ERINGEN, A. C. and KAFADAR, C. B. Continuum Physics, Vol. Ⅳ. Academic Press, New York, 1-73 (1976)
|
| [37] |
LU, Z. J. Micropolar continuum mechanics is more profound than classical continuum mechanics. Applied Mathematics and Mechanics (English Edition), 8(10), 939-946 (1987) doi:10.1007/BF02454256 |
| [38] |
LUKASZEWICZ, G. Micropolar Fluids:Theory and Applications, Birkhäuser, Boston (1999)
|
| [39] |
DYSZLEWICZ, J. Micropolar Theory of Elasticity, Springer, New York (2004)
|
| [40] |
IESAN, D. Classical and Generalized Models of Elastic Rods, CRC Press, Boca Raton (2009)
|
| [41] |
PIETRASZKIEWICZ, W. and EREMEYEV, V. A. On natural strain measures of the non-linear micropolar continuum. International Journal of Solids and Structures, 46(3-4), 774-787 (2009) doi:10.1016/j.ijsolstr.2008.09.027 |
| [42] |
ALTENBACH, H. and EREMEYEV, V. A. Strain rate tensors and constitutive equations of inelastic micropolar materials. International Journal of Plasticity, 63, 3-17 (2014) doi:10.1016/j.ijplas.2014.05.009 |
| [43] |
ANSARI, R., SHAKOURI, A. H., BAZDID-VAHDATI, M., NOROUZZADEH, A., and ROUHI, H. A nonclassical finite element approach for the nonlinear analysis of micropolar plates. Journal of Computational Nonlinear Dynamics, 12(1), 011019 (2017) |
| [44] |
KRÖNER, E. Elasticity theory of materials with long range cohesive forces. International Journal of Solids and Structures, 3, 731-742 (1967) doi:10.1016/0020-7683(67)90049-2 |
| [45] |
KRUMHANSL, J. Some Considerations of the Relation between Solid State Physics and Generalized Continuum Mechanics, IUTAM symposia, Springer, Berlin/Heidelberg, 298-311 (1968)
|
| [46] |
KUNIN, I. A. The Theory of Elastic Media with Microstructure and the Theory of Dislocations, IUTAM symposia, Springer, Berlin/Heidelberg, 321-329 (1968)
|
| [47] |
ERINGEN, A. C. Nonlocal polar elastic continua. International Journal of Engineering Science, 10, 1-16 (1972) doi:10.1016/0020-7225(72)90070-5 |
| [48] |
ERINGEN, A. C. and EDELEN, D. G. B. On nonlocal elasticity. International Journal of Engineering Science, 10, 233-248 (1972) doi:10.1016/0020-7225(72)90039-0 |
| [49] |
ERINGEN, A. C. On differential equations of nonlocal elasticity and solutions of screw dislocation and surface waves. Journal of Applied Physics, 54, 4703-4710 (1983) doi:10.1063/1.332803 |
| [50] |
ZHAO, H. S., ZHANG, Y., and LIE, S. T. Frequency equations of nonlocal elastic micro/nanobeams with the consideration of the surface effects. Applied Mathematics and Mechanics (English Edition), 39(8), 1089-1102 (2018) doi:10.1007/s10483-018-2358-6 |
| [51] |
EBRAHIMI, F. and BARATI, M. R. Dynamic modeling of preloaded size-dependent nanocrystalline nano-structures. Applied Mathematics and Mechanics (English Edition), 38(12), 1753-1772 (2017) doi:10.1007/s10483-017-2291-8 |
| [52] |
GUVEN, U. General investigation for longitudinal wave propagation under magnetic field effect via nonlocal elasticity. Applied Mathematics and Mechanics (English Edition), 36(10), 1305-1318 (2015) doi:10.1007/s10483-015-1985-9 |
| [53] |
LI, C. Torsional vibration of carbon nanotubes:comparison of two nonlocal models and a semicontinuum model. International Journal of Mechanical Science, 82, 25-31 (2014) doi:10.1016/j.ijmecsci.2014.02.023 |
| [54] |
LI, C., LI, S., YAO, L., and ZHU, Z. Nonlocal theoretical approaches and atomistic simulations for longitudinal free vibration of nanorods/nanotubes and verification of different nonlocal models. Applied Mathematical Modelling, 39(15), 4570-4585 (2015) doi:10.1016/j.apm.2015.01.013 |
| [55] |
ANSARI, R., GHOLAMI, R., SAHMANI, S., NOROUZZADEH, A., and BAZDID-VAHDATI, M. Dynamic stability analysis of embedded multi-walled carbon nanotubes in thermal environment. Acta Mechanica Solida Sinica, 28(6), 659-667 (2015) doi:10.1016/S0894-9166(16)30007-6 |
| [56] |
SHEN, J. P. and LI, C. A semi-continuum-based bending analysis for extreme-thin micro/nanobeams and new proposal for nonlocal differential constitution. Composite Structures, 172, 210-220 (2017) doi:10.1016/j.compstruct.2017.03.070 |
| [57] |
NOROUZZADEH, A. and ANSARI, R. Isogeometric vibration analysis of functionally graded nanoplates with the consideration of nonlocal and surface effects. Thin-Walled Structures, 127, 354-372 (2018) doi:10.1016/j.tws.2017.11.040 |
| [58] |
CHALLAMEL, N. and WANG, C. M. The small length scale effect for a non-local cantilever beam:a paradox solved. Nanotechnology, 19(34), 345703 (2008) doi:10.1088/0957-4484/19/34/345703 |
| [59] |
NOROUZZADEH, A., ANSARI, R., and ROUHI, H. Pre-buckling responses of Timoshenko nanobeams based on the integral and differential models of nonlocal elasticity:an isogeometric approach. Applied Physics A, 127, 330 (2017) |
| [60] |
FARAJI-OSKOUIE, M., ANSARI, R., and ROUHI, H. Bending of Euler-Bernoulli nanobeams based on the strain-driven and stress-driven nonlocal integral models:a numerical approach. Acta Mechanica Sinica, 34(5), 871-882 (2018) doi:10.1007/s10409-018-0757-0 |
| [61] |
MAHMOUDPOUR, E., HOSSEINI-HASHEMI, S. H., and FAGHIDIAN, S. A. Nonlinear vibration analysis of FG nano-beams resting on elastic foundation in thermal environment using stress-driven nonlocal integral model. Applied Mathematical Modelling, 57, 302-315 (2018) doi:10.1016/j.apm.2018.01.021 |
| [62] |
FARAJI-OSKOUIE, M., ANSARI, R., and ROUHI, H. A numerical study on the buckling and vibration of nanobeams based on the strain- and stress-driven nonlocal integral models. International Journal of Computational Materials Science and Engineering, 7, 7, 1850016 (2018) doi:10.1142/S2047684118500161 |
| [63] |
NOROUZZADEH, A., ANSARI, R., and ROUHI, H. Isogeometric vibration analysis of small-scale Timoshenko beams based on the most comprehensive size-dependent theory. Scientia Iranica, 25, 1864-1878 (2018) |
| [64] |
NOROUZZADEH, A. and ANSARI, R. Finite element analysis of nano-scale Timoshenko beams using the integral model of nonlocal elasticity. Physica E, 88, 194-200 (2017) doi:10.1016/j.physe.2017.01.006 |
| [65] |
FERNÁNDEZ-SÁEZ, J., ZAERA, R., LOYA, J. A., and REDDY, J. N. Bending of Euler-Bernoulli beams using Eringen's integral formulation:a paradox resolved. International Journal of Engineering Science, 99, 107-116 (2016) doi:10.1016/j.ijengsci.2015.10.013 |
| [66] |
ROMANO, G., BARRETA, R., and DIACO, M. On nonlocal integral models for elastic nanobeams. International Journal of Mechanical Science, 131, 490-499 (2017) |
| [67] |
MAHMOUD, F. F. On the nonexistence of a feasible solution in the context of the differential form of Eringen's constitutive model:a proposed iterative model based on a residual nonlocality formulation. International Journal of Applied Mechanics, 9(7), 1750094 (2017) doi:10.1142/S1758825117500946 |
| [68] |
ANSARI, R., TORABI, J., and NOROUZZADEH, A. Bending analysis of embedded nanoplates based on the integral formulation of Eringen's nonlocal theory using the finite element method. Physica B, 534, 90-97 (2018) doi:10.1016/j.physb.2018.01.025 |
| [69] |
NOROUZZADEH, A., ANSARI, R., and ROUHI, H. Isogeometric analysis of Mindlin nanoplates based on the integral formulation of nonlocal elasticity. Multidiscipline Modeling in Materials and Structures, 14(5), 810-827 (2018) doi:10.1108/MMMS-09-2017-0109 |
| [70] |
LAKES, R. Experimental microelasticity of two porous solids. International Journal of Solids and Structures, 22, 55-63 (1986) doi:10.1016/0020-7683(86)90103-4 |
| [71] |
LI, L. and HU, Y. Nonlinear bending and free vibration analyses of nonlocal strain gradient beams made of functionally graded material. International Journal of Engineering Science, 107, 77-97 (2016) doi:10.1016/j.ijengsci.2016.07.011 |
| [72] |
XU, X. J., WANG, X. C., ZHENG, M. L., and MA, Z. Bending and buckling of nonlocal strain gradient elastic beams. Composite Structures, 160, 366-377 (2017) doi:10.1016/j.compstruct.2016.10.038 |
| [73] |
NOROUZZADEH, A., ANSARI, R., and ROUHI, H. Nonlinear wave propagation analysis in Timoshenko nano-beams considering nonlocal and strain gradient effects. Meccanica, 53(13), 3415-3435 (2018) doi:10.1007/s11012-018-0887-2 |
| [74] |
NOROUZZADEH, A., ANSARI, R., and ROUHI, H. Nonlinear bending analysis of nanobeams based on the nonlocal strain gradient model using an isogeometric finite element approach. Iranian Journal of Science and Technology, Transactions of Civil Engineering, 1-15 (2018) doi:10.1007/s40996-018-0184-2 |

 2019, Vol. 40
2019, Vol. 40


