Shanghai University
Article Information
- AZARIPOUR S., BAGHANI M.
- Vibration analysis of FG annular sector in moderately thick plates with two piezoelectric layers
- Applied Mathematics and Mechanics (English Edition), 2019, 40(6): 783-804.
- http://dx.doi.org/10.1007/s10483-019-2468-8
Article History
- Received Jul. 4, 2018
- Revised Sep. 13, 2018
Functionally graded materials (FGMs), first proposed by a group of material scientists in Japan[1], are classified in the composite category because their mechanical properties usually change smoothly through their thickness[2]. One of the typical kinds of FGMs is a powdered mixture of metal and ceramic. Metal matrix composites and FGMs are commonly considered in micromechanical models[3-4].
One of the most critical structures widely used in various engineering installations, including vehicle and aerospace industries, is the plate[5]. Sector and annular sector plates are used in many engineering constructions, and aeronautical applications and numerous studies on the behavior of these structures have been conducted[6-12].
The study of moderately thick plates requires taking shear deformation and rotary inertia effects into account, and this is the primary hypothesis in the first-order shear deformation (FSD) plate theory. Since these effects are not taken into account in the classical plate (CP) theory, the results from these methods underestimate deflections and overestimate buckling loads as well as natural frequencies. Less complexity in computational procedures with an acceptable accuracy of the FSD theory leads to the typical application of this theory rather than higher-order methods.
Piezoelectric materials have many applications in electronics, ultrasonic and smart structures. From one point of view, based on electric boundary conditions, they can have open and closed circuit conditions[13-14]. Closed circuit piezoelectric layers are mainly used in actuators, and an open circuit condition is applicable in designing layers of piezoelectric sensors. Dynamic behaviors of FG and piezoelectric materials have a crucial rule in the mechanical systems. In the following, some of them are expressed.
Wang et al.[15] presented a direct displacement method to investigate the free axisymmetric vibration of transversely isotropic circular plates, whose material is functionally graded (FG) and properties obey the exponential law along the thickness direction of the plate. Chen et al.[16] proposed a new method of state-space-based differential quadrature presented for free vibration of generally laminated beams, and they established new state equations at discrete points by discretizing the state space formulations along the axial direction using the technique of differential quadrature. Wang and Li[17] studied the free vibration response of FGM beams and derived the natural frequency of an FGM Levinson beam analytically in terms of the natural frequency of a corresponding homogenous Euler-Bernoulli beam. Sohn et al.[18] considered the dynamic characteristics of an end-capped hull structure with piezoelectric actuators. They studied a linear quadratic Gaussian (LQG) theory to suppress the vibration of the smart hull structure. Cheng et al.[19] studied a two-degree-of-freedom piezoelectric motor using only one piezoelectric ceramic and established analytical and numerical models in order to design the piezoelectric vibrator. Li and Song[20] analyzed the free and forced vibration behaviors of the two-span beams with the piezoelectric actuators and sensors. Javanbakht et al.[21] presented the elasticity solution of the FG shell with two piezoelectric layers. They considered the numerical results for an FG cylindrical shell with a piezoelectric layer as an actuator in the external surface and a piezoelectric layer as an sensor in the internal surface. Arefi et al.[22] presented the three-dimensional vibration analysis of an FG cylindrical shell integrated by two thin FG piezoelectric (FGP) layers. Mohammadimehr and Rostami[23] analyzed the bending and free vibration of a rotating sandwich cylindrical shell with the consideration of the nanocomposite core and piezoelectric layers. There are many investigations in the literature on the behavior of annular circular plates with piezoelectric layers, and some of them are mentioned below. Wang et al.[24] investigated the free vibration of circular plates integrated with two piezoelectric layers based on the CP theory. In their study, the distribution of electrical potential in piezoelectric layers along the thickness was simulated employing a quadratic function, and only the closed-circuit electric boundary condition was considered. Keleshteri et al.[25] studied the vibration of FG carbon nanotube (FG-CNT) reinforced composite annular plates integrated with piezoelectric layers on an elastic foundation. In their work, both closed and open circuit electrical boundary conditions were taken into account. Wu et al.[26] were the first group to find a solution for satisfying the open circuit electric boundary condition for the aforementioned structure. An analytical solution based on the transformation of variables for free vibration of annular circular plates with two piezoelectric layers was presented by Duan et al.[27]. In their work, two plate theories (CP and FSD) were considered, and it was observed that the results obtained with the FSD theory are compared with those of the CP theory. In their study, the distribution of electrical potential was assumed to be a sinusoidal function, and the piezoelectric layers were shortly connected (the closed circuit condition). Ebrahimi and Rastgoo[28-29] studied free vibration of circular and annular circular thin FG plates integrated with two piezoelectric layers as actuators. Hashemi et al.[30] applied a third-order shear deformation (TSD) plate theory to study the free vibration of thick annular FG plates integrated with two piezoelectric layers.
In this paper, a generalized differential quadrature (GDQ) method is used to discretize these six equations developed based on the FSD plate theory and using Hamilton's principle with parameters satisfying Maxwell's electrostatics equation in piezoelectric layers. Applying a small number of grid points in the domain of solution is one of the main advantages of the GDQ method in comparison with other common numerical methods that could be observed in the presented results. In the next step, the results are extracted using the GDQ method. To show the accuracy of the proposed solution, the results are compared with those in the literature. Finally, the effects of piezoelectric layers, FG plate thickness, power law index in FGMs, and plate geometrical parameters such as the angle of the sector and annular sector radii on the in-plane and out-of-plane natural frequencies with different electrical and mechanical boundary conditions are investigated in detail.
2 FGMsIt is assumed that FGMs are made of ceramic and metal, and their mechanical properties vary continuously and smoothly through the thickness z from pure metal to pure ceramic according to the power distribution law in terms of volume fraction as
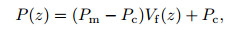
|
(1) |
where P is a general material property such as Young's modulus E and the density ρ since the wline variation of Poisson's ratio v through the thickness is not substantial. Therefore, this ratio is assumed to be constant (v =0.3). In Eq. (1), subscripts m and c refer to metal and ceramic, respectively, and the volume fraction Vf is defined as[31]
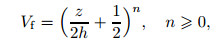
|
(2) |
where n denotes the power law index of FGMs and takes only positive values, 2h is the thickness of the plate, and z stands for the thickness from pure metal to pure ceramic.
3 Constitutive relations based on FSD theory 3.1 Displacement fieldConsider a moderately thick annular sector FG plate with two piezoelectric layers on the top and bottom surfaces with the sector angle α, inner radius ri, and outer radius ro, as depicted in Fig. 1. The thickness of FG plate is 2h, and the thickness of each piezoelectric layer is hp. The coordinates are chosen such that the rθ -plane lies on the middle surface of FG plate. Based on the FSD theory, the displacement field can be stated as follows[32]:
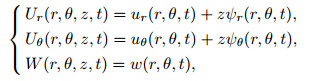
|
(3) |
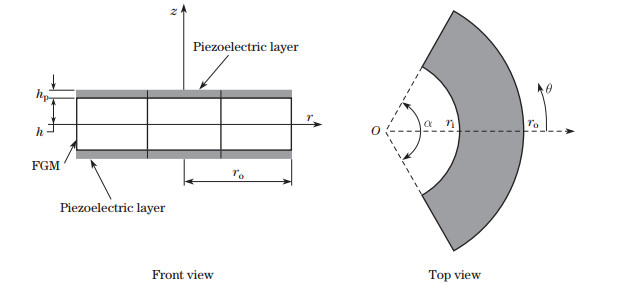
|
| Fig. 1 Geometry and coordinate of two piezoelectric layers coupled with FG annular sector plate |
|
|
where ur and uθ are in-plane displacements in the r- and θ-directions, respectively, w is the transverse displacement in the z-direction, and t is the time. ψr and ψθ are the rotations of the mid-plane about θ- and r-directions, respectively.
3.2 Strain and stress fieldStrain-displacement relations using the displacement field given in Eq. (3) are recast as
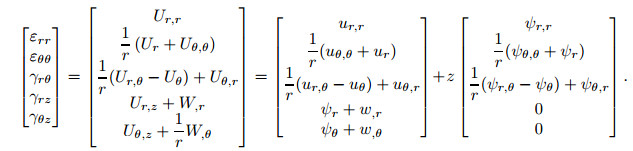
|
(4) |
Stress-strain relations based on Hook's law for an FG host plate are stated in the following equation:
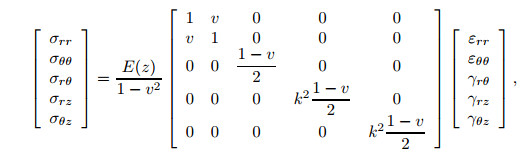
|
(5) |
where σi, j and εi, j (i, j = r, θ, z) are stress and strain components, respectively, and k2 is the shear correction factor and is assumed to be π2/12[27].
4 Piezoelectric layersIn order to satisfy open and closed circuit electrical boundaryconditions, an electric potential function along the thicknessdirection of piezoelectric layers is assumed to be[33]
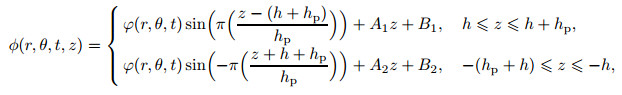
|
(6) |
where φ (r, θ, t) denotes the electrical potential inthe mid-surface of each piezoelectric layer, and parameters A1, B1, A2, and B2 are functions of r, θ, and t, which would be determined by satisfying closed and openelectrical boundary conditions on the surfaces of piezoelectriclayers. It is assumed that piezoelectric layers (for closed and opencircuit conditions) on the top and bottom surfaces of the host plate(z=±h) are surface bonded so that the potential function, asgiven in Eq. (6), can satisfy the boundary condition in Eq. (7). Aforementioned boundary conditions are acceptable for the other side(z=±(h+hp)) of the closed circuit piezoelectriclayers (actuators). However, for the open circuit, the oppositesurfaces of piezoelectric layers should satisfy the boundarycondition in Eq. (8), and these conditions are satisfied via thethoroughly insulated surface on sensor layers[26], i.e.,
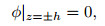
|
(7) |
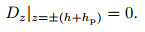
|
(8) |
The following values for parameters A1, B1, A2, and B2 are defined by putting Eqs. (7) and (8) for open and closedelectrical boundary conditions into the electrical potentialfunction given by Eq. (6):
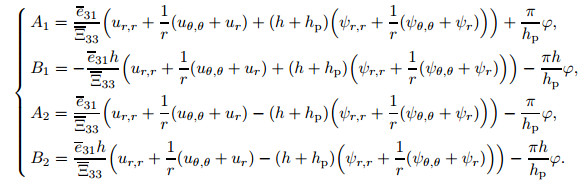
|
(9) |
Constitutive relations in piezoelectric layers based on theassumption of polarization of piezoelectric layers along thethickness direction are obtained as[27]

|
(10) |
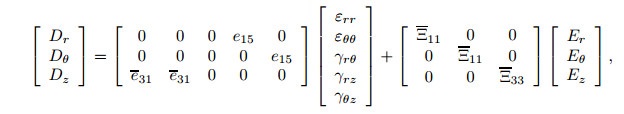
|
(11) |
where {D} and {E} are electric displacement and field components, respectively. [CE], [Ξ], and [e] are reduced piezoelectric material constants, defined as
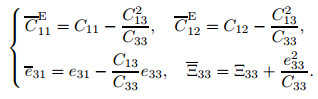
|
(12) |
[CE], [Ξ], and [e]are elastic constants, dielectric permittivity, and electromechanical coupling, respectively. Electric fields along r-, θ-, and z-directions are defined as follows:
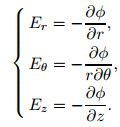
|
(13) |
The kinetic energy T and strain energy V of an FG annular sectorplate with two piezoelectric layers are expressed as
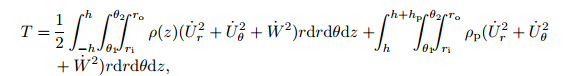
|
(14) |
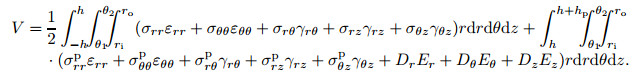
|
(15) |
The partial differentiation with respect to time t in Eq. (14) isshown by a superimposed dot. ρ and ρp are the densities of the host FG plate andpiezoelectric layers, respectively. Applying Hamilton's principle
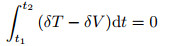
|
(16) |
gives five coupled equations of motion for the dynamic behavior ofannular sector FG plates with two piezoelectric layers as follows:
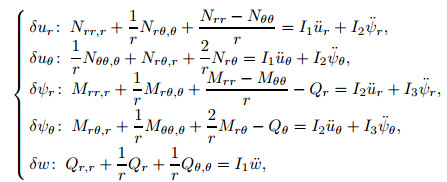
|
(17) |
where Ni, j, Mi, j, and Qi(i, j=r, θ) are thein-plane force, twisting moment, and transverse force resultants, respectively, which are defined in the following equations:
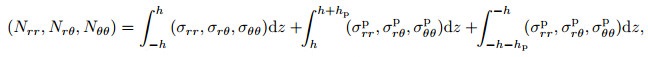
|
(18) |
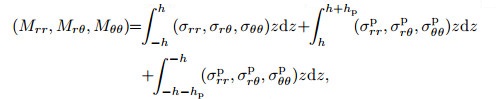
|
(19) |
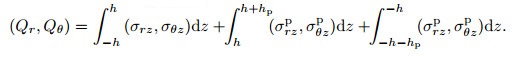
|
(20) |
Mass moments of inertias I1, I2, and I3 are defined as
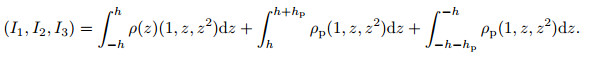
|
(21) |
Substituting Eqs. (18)-(20) into Eq. (17) arrives at thefollowing equations:
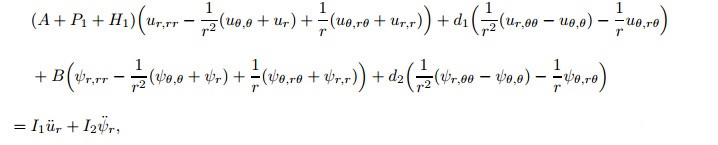
|
(22a) |
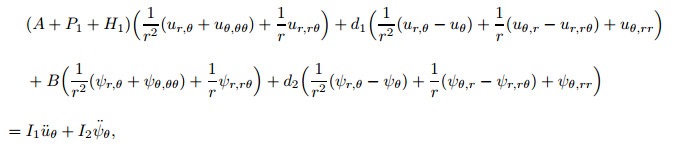
|
(22b) |
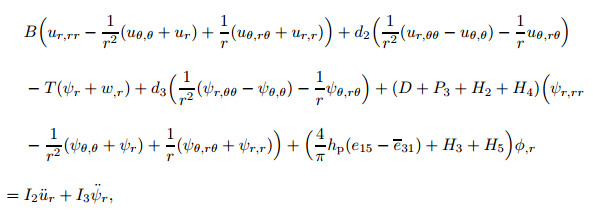
|
(22c) |
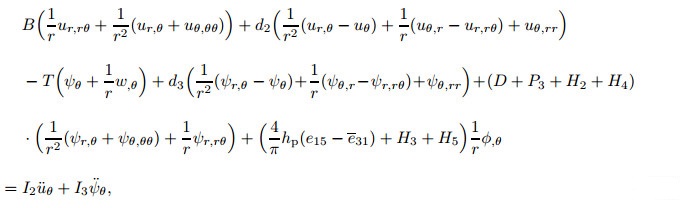
|
(22d) |
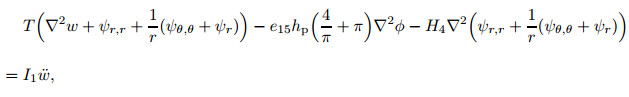
|
(22e) |
where ▽2 is the Laplace operator in polar coordinates, andother coefficients in Eq. (22) are introduced as
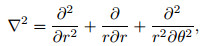
|
(23) |
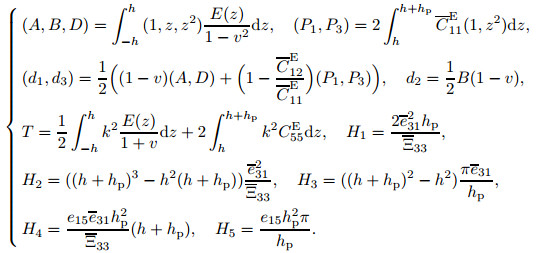
|
(24) |
Satisfying Maxwell's electrostatic equation by all electricalvariables in piezoelectric layers is necessary, which requiresvanishing electric flux density divergence at any point within thepiezoelectric media. Enforcing the integration of the divergence ofelectric flux density across the thickness of piezoelectric layersfor any r an θ to be zero, Maxwell's equationcould be approximately satisfied as[34]
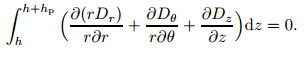
|
(25) |
Substituting Eq. (11) into Eq. (25) and with some simplifications, one may obtain the following equation:
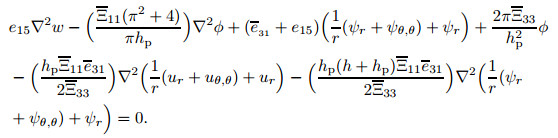
|
(26) |
Mechanical boundary conditions along theannular sector edges are presented as follows:
For clamped edge,
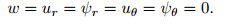
|
(27) |
For simply supported edge,
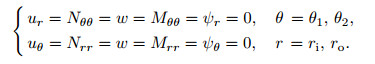
|
(28) |
For free edge,
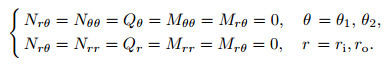
|
(29) |
Two types of boundary conditions for the piezoelectric layers' edgescan be considered.
(ⅰ) Edges are electrically earthed (ϕ =0) which is used inshortly connected piezoelectric layers.
(ⅱ) Edges with the open circuit boundary condition are electrically insulated. In this case, the following conditions should be considered:
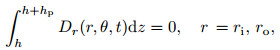
|
(30) |
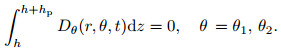
|
(31) |
Finally, in order to solve six coupled partial differential equations (see Eqs. (22a)-(22e) and (26)) with an arbitrary combination of boundary conditions (see Eqs. (27)-(31)), the GDQ method is used as follows.
6 GDQ methodThe GDQ method is a numerical method with a fast rate of convergence which requires fewer grid points in the domain solution. The capability of the GDQ method to handle engineering problems has been demonstrated in Refs. [35]-[37]. The approximation of partial derivative of a function with respect to the independent variable by a weighted sum of function values in all discrete grid points in the independent variable direction is the basis of the GDQ method. For instance, the mth-order derivative of a function f(r) in the direction of an independent variable r at the ith-discrete point (r = ri) is defined as[38]
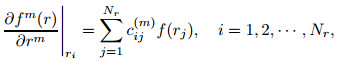
|
(32) |
where Nr is the total number of grid points along the r-direction, and cij(m) are weighting coefficients.Lagrange interpolation polynomials are used to obtain weighting coefficients. For the first derivative, the weighting coefficientrelation is presented as[38]
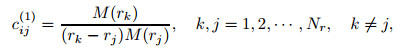
|
(33) |
where
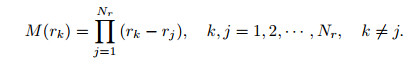
|
(34) |
For higher-order derivatives, a recursive equation is used[38],
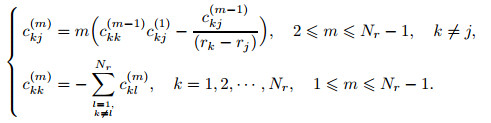
|
(35) |
Although choosing equal distances between grid points in the domain is the simplest way in the discretization of the domain, the Chebyshev distribution is the best option (see Eq. (36)). It is shown that it leads to more reliable and accurate results by considering compact grid points around boundaries[39],
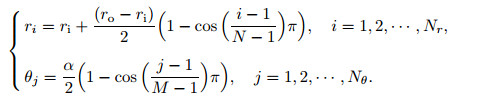
|
(36) |
The domain is divided into Nr×Nθ grid points, where Nr and Nθ are the numbers of gridpoints in the r- and θ-directions, respectively. Rewriting the governing equations (22) and (26) and boundary conditions (27)-(31) using an approximation of derivatives is performed in the next step. For example, the discretized form of Eq. (22a) could be written as follows:
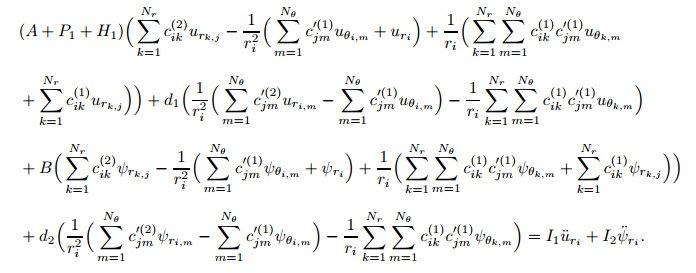
|
(37) |
Finally, by discretization, the entire governing equations withboundary conditions based on the GDQ method, 5× (Nr×Nθ) algebraic equations, are obtained, where solving them gives natural frequencies and relative mode shapes of the structure.
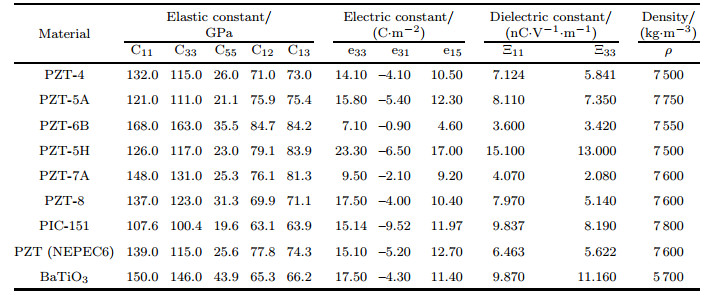
7 Materials propertiesTable 1 summarizes the mechanical properties of the host plate, and Table 2 shows the properties of piezoelectric materials.
In this section, the numerical results computed for free vibration of moderately thick FG annular sector plates embedded with two piezoelectric layers with various combinations of boundary conditions are presented. The symbols S, F, and C represent simply supported, free, and clamped, respectively. For convenience, boundary conditions of an annular sector plate are defined by the combination of the three symbols, such as CCCC, SFCF, and FCFC. For instance, SFCF stands for the simply supported, free, clamped, and free boundary conditions of edges 1, 2, 3, and 4 on the plate, respectively, as shown in Fig. 2. In order to make the natural frequencies dimensionless, the following equation is used:
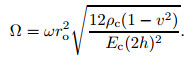
|
(38) |
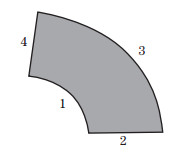
|
| Fig. 2 Annular sector plate with specific edges |
|
|
In order to show the convergence of GDQ results and find an optimum number of grid points in the domain, the convergences of various examples are investigated as shown in Figs. 3 and 4. In these figures, ωc represents completely converged results of the proposed method (with 5 meaningful digits). Very good convergences of the results for different combinations of boundary conditions with various geometric parameters (including the thicknesses of host plate 2h and piezoelectric layers hp, the ratio of the inner radius to the outer radius ri/ro, and the angle of sector α for different materials of FG plate and piezoelectric layers are shown in Figs. 3 and 4. Figure 3 depicts the convergences of the first four modes of vibration for an annular sector sector Al/Al2O3 plate[43] with two PZT-4 shortly connected piezoelectric layers for different combinations of boundary conditions. While Fig. 4 illustrates the convergences of annular sector Al/ZrO2 plate with two BaTiO3 piezoelectric materials for different angles and both open and closed circuit electrical boundary conditions.
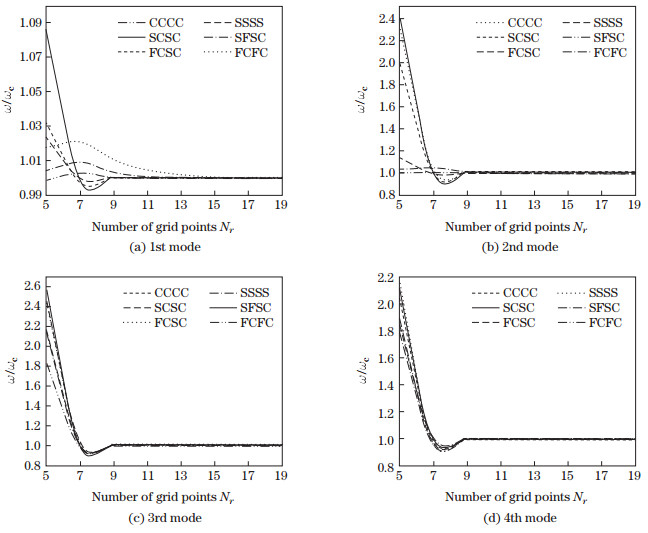
|
| Fig. 3 Convergences of normalized frequency parameter ω/ωc for the first four modes of annular sector plate with two piezoelectric layers and different boundary conditions, where hp/(2h)=0.1, 2h/ro=0.05, n=1, ri/ro=0.3, α =60℃, and Nr=Nθ |
|
|
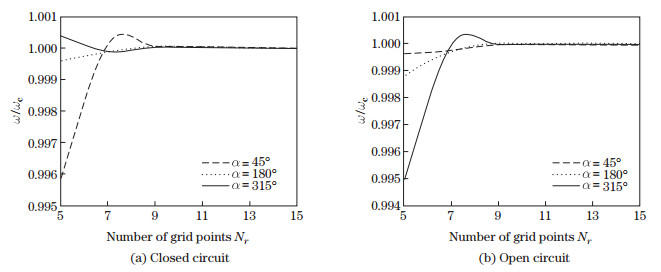
|
| Fig. 4 Convergences of normalized frequency parameter ω/ωc of FG annular sector platewith two piezoelectric layers under CCCC boundary condition, whereh hp/(2h)=0.1, 2h/ro=0.07, n=1, ri/ro=0.5, and Nr=Nθ |
|
|
It is worth mentioning that the number of grid points along the r-direction Nr is assumed to be equal to the number of grid points along the θ-direction Nθ in all presented results.
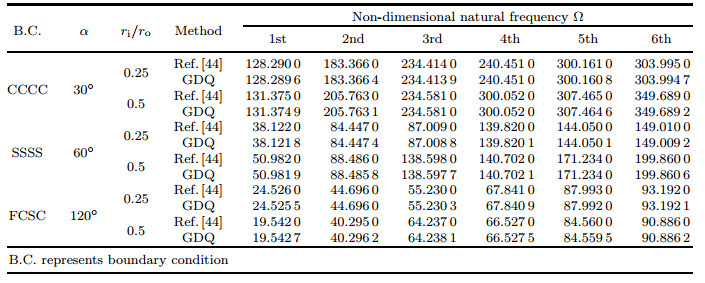
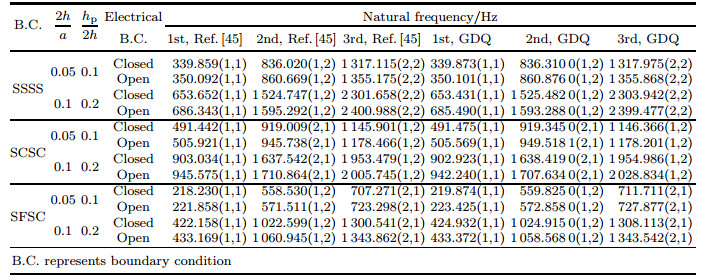
In order to investigate the accuracy of the solution, some comparisons are made between the results computed by the proposed method and those presented by Liew and Liu[44] for annular sector plates shown in Table 3. In this paper, the free vibration of FG annular sector plate with two piezoelectric layers is investigated for the first time. In order to show the accuracy of the proposed method when two piezoelectric layers are coupled with a host plate, the GDQ results for FG rectangular plates are compared with those reported by Farsangi and Saidi[45], as summarized in Table 4.
 |
 |
The first six modes of out-of-plane natural frequencies of isotropic annular sector plates with different combinations of boundary conditions, the ratio of the inner radius to the outer radius, and the angle of sector plates are summarized in Table 3. In this table, errors between GDQ results and those obtained by Liew and Liu[44] are almost negligible, and the maximum accuracy of the solution is shown.
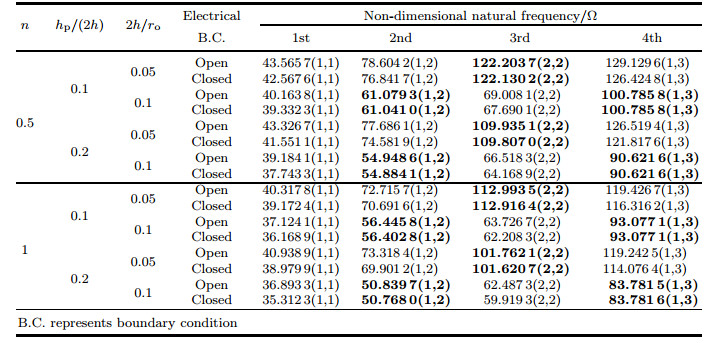
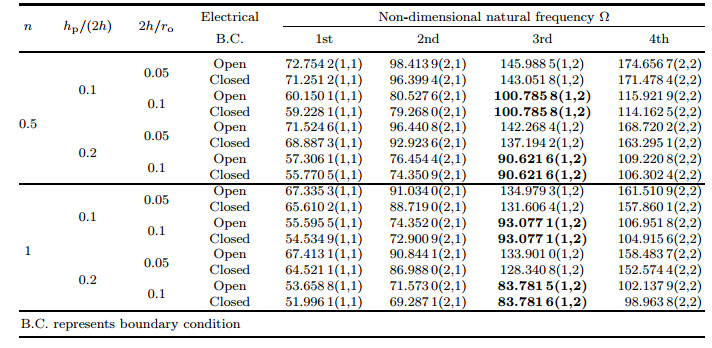
As mentioned previously, to the best of our knowledge, results for annular sector FG plates embedded with two piezoelectric layers have not been reported in the literature. For this case, in order to investigate the accuracy of the results obtained with the proposed method, a square FG plate (with the length and width a) as a specific kind of annular plate (ri= 99.5, ro= 100.5, and α =0.572 96°) is considered. Table 4 shows comparisons between GDQ results and those presented by Farsangi and Saidi[45] for FG square plates with two PZT-4 piezoelectric layers under open and closed circuit electrical boundary conditions and different combinations of mechanical boundary conditions, hp/(2h), and 2h/a for different modes of vibration. In this table, numbers in parenthesis indicate the mode numbers along the x- and y-directions, and only out-of-plane natural frequencies are considered. It is worth mentioning that the results presented by Farsangi and Saidi[45] are based on the assumption that electrical potentials along the x- and y-directions are zero and insulated, respectively, due to a Levy type solution used in their study. This assumption is not accurate when piezoelectric layers are insulated entirely (open circuit condition) or shortly connected. This leads to some inconsistencies in the results. Therefore, a maximum error of about 1% between the results in Table 4 is a good evidence for the mentioned allegation. By comparing the results presented in Tables 3 and 4, it is observed that the present results are in perfect accord with those shown in the previous literature.
8.2 Effects of different parameters on natural frequenciesIn this section, the impacts of various parameters, such as different power distribution laws of the FG plate, piezoelectric and host plate thicknesses, angle and ratio of the inner radius to outer radius of an annular sector, and properties of FG and piezoelectric materials on the vibration response are studied. Also, effects of different combinations of mechanical (clamped, simply supported, and free) and electrical (open and close circuit) boundary conditions on natural frequencies are investigated.
The natural frequency is a function of power index for an annular FG plate. The natural frequencies of the system decrease by increasing n and stabilize for the values of n higher than six. Figures display the variation of the fundamental frequency versus the thickness of host plate h for different values of volume fraction exponent for an annular FG plate. It is obviously observed that, with the enhancement of the thickness of host plate, the fundamental frequency increases for any volume fraction exponent. It can also be observed that the fundamental frequency decreases as the power index n increases[30].
For FG (Al/Al2O3) annular sector plates with 2h/ro=0.05 and two PZT-4 piezoelectric layers with hp/(2h)=0.1, the effects of angle α, ratio of inner radius to outer radius ri/ro, and different mechanical boundary conditions (SSSS, CCCC, and SFCS) under both open and closed circuit electrical boundary conditions are investigated in Fig. 5. These figures show that, increasing the ratio of the inner radius to the outer radius, natural frequencies are increased due to the higher stiffness of the structure. The slopes of the graphs in Fig. 5 are higher for larger values of ri/ro. This shows a rapid growth in the stiffness of the structures. Increasing the angle of the sector leads to small natural frequencies. This phenomenon occurs because for larger values of ri/ro the annular sector plate behaves like a curved beam, and the effects of the angle of the curved beams on the natural frequencies are less than annular sector plates.
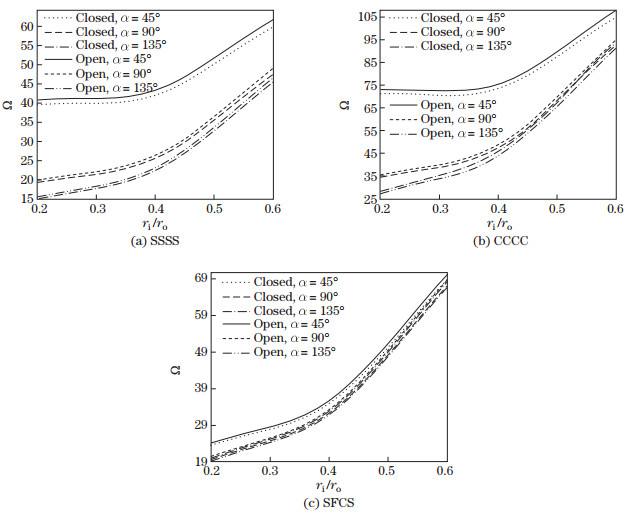
|
| Fig. 5 Non-dimensional fundamental natural frequencies of annular sector Al/Al2O3 plate coupled with PZT-4 piezoelectric layers under different boundary conditions, where hp/(2h) = 0.1, 2h/ro = 0.05, and n = 1 |
|
|
Figure 6 plots the effects of the angle of annular sector plate and piezoelectric materials on fundamental natural frequencies. In these figures, three types of piezoelectric materials (BaTiO3, PIC-151, and PZT-7A) and different boundary conditions (CCCC, CCSF, SSSS, and FSCF) for the closed circuit electrical boundary condition are considered. These figures show that the difference in natural frequencies for angles above 180° is tiny.
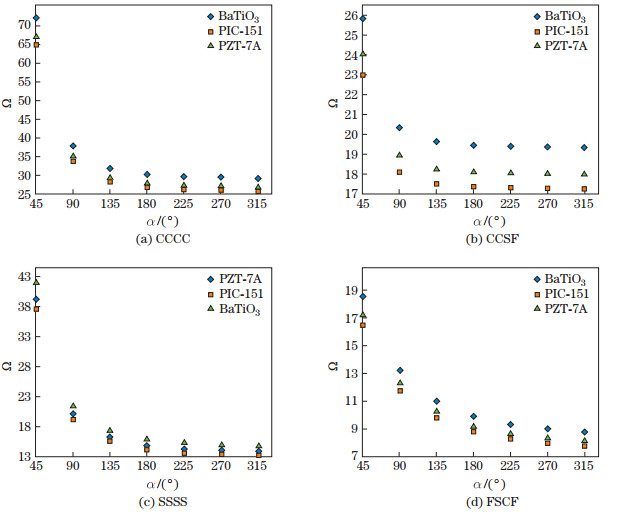
|
| Fig. 6 Non-dimensional fundamental natural frequencies of annular sector Al/Al2O3 plate coupled with various piezoelectric layers with different boundary conditions, where hp/(2h) = 0.1, 2h/ro = 0.07, and n = 1 and ri/ro=0.25 |
|
|
Figures 5 and 6 show larger natural frequencies with the open circuit electrical boundary condition in comparison with the closed circuit ones. Since electrical potentials on the surfaces of shortly connected piezoelectric layers (closed circuit condition) are zero, the electric energy is released when the plate vibrates. On the other hand, the surfaces under the open circuit boundary condition are potentially insulated. Thus, the electric energy could not be released, and it is converted into the mechanical energy, which leads to higher natural frequencies. Therefore, the assumption of insulated condition on the piezoelectric surfaces (sensors) produces higher natural frequencies than the earthed condition (actuators).
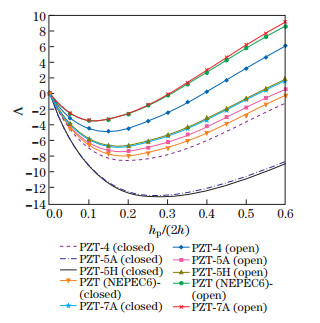
In order to study the effects of piezoelectric materials on thenatural frequencies, non-dimensional fundamental natural frequenciesof an annular sector Al/Al2O3 plates with ri/ro=0.5, 2h/ro=0.05, α =60°, and n=1 under SSSS and CCCC mechanical boundary conditions for both open and closed electrical boundary conditions are presented in Figs. 7 and 8. To give a better view in these figures, a parameter Λ is defined as follows:
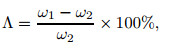
|
(39) |
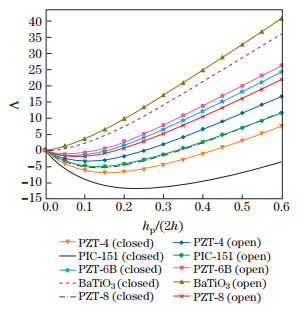
|
| Fig. 7 Variations of Λ for FG annular sector plate coupled with various piezoelectric layers with SSSS boundary condition (color online) |
|
|
|
| Fig. 8 Variations of Λ for FG annular sector plate coupled with various piezoelectric layers that are not considered in Fig. 7 with SSSS boundary condition (color online) |
|
|
where ω1 and ω2 represent the frequencies with andwithout piezoelectric layers, respectively.
Figures 7 and 8 reveal that, for a larger thickness of piezoelectric layers, the rigidity of the entire structure increases, and consequently higher natural frequencies are expected. However, firstly a decrease is observed in the natural frequency. The piezoelectricity effect of the piezoelectric layers is a reasonable justification for this phenomenon. When piezoelectric layer thicknesses are small, the piezoelectricity overcomes rigidity, and for larger thicknesses of piezoelectric layers to some extent, the rigidity overcomes the piezoelectricity which could increase natural frequencies. This phenomenon is more noticeable in PZT-5H and PZT-5A, while BaTiO3 has a minimal piezoelectricity effect in comparison with the other piezoelectric materials studied in this work.
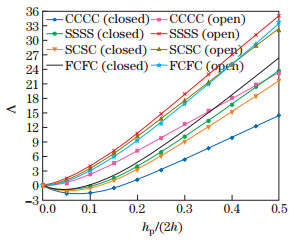
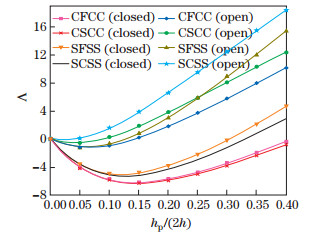
Figures 9 and 10 show the same phenomenon for different boundary conditions including CCCC, SSSS, SCSC, FCFC, CFCC, CSCC, SFSS, and SCSS for PZT-4 and PIC-151 for an annular sector Al/ZrO2 plate with 2h/ro=0.05, ri/ro=0.4, α=90°, and n=1. According to Figs. 9 and 10, CCCC and SCSC boundary conditions for PZT-4, and CSCC and CFCC boundary conditions for PIC-151 with the closed circuit electrical boundary condition have the strongest piezoelectricity effects.
|
| Fig. 9 Variations of Λ for FG annular sector plate coupled with PZT-4 piezoelectric layers with different boundary conditions (color online) |
|
|
|
| Fig. 10 Variations of Λ for FG annular sector plate coupled with PIC-151 piezoelectric layers with different boundary conditions (color online) |
|
|
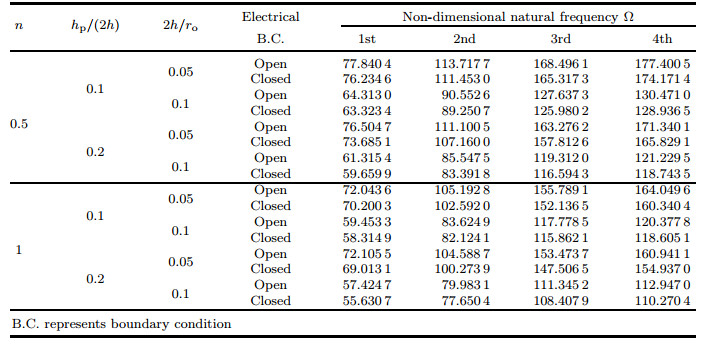
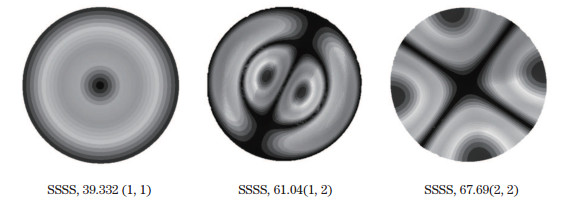
In order to distinguish between in-plane and out-of-plane natural frequencies, the motion of the plate along the r- and θ-directions is assumed to be zero, and this assumption gives only out-of-plane natural frequencies. Tables 5-7 tabulate the first four non-dimensional natural frequencies for an annular sector Al/Al2O3 plate coupled with twoPZT-4 piezoelectric layers with ri/ro=0.5 and α =60° for CCCC, SSSS, and CSCS boundary conditions. As shown, in the first four modes of vibration under the CCCC boundary condition, the in-plane vibration mode is not observed, and all modes are out-of-plane. Tables 6 and 7 reveal that increasing the thickness of the structure, the number of in-plane vibration modes is also increased. In Tables 6-9, the corresponding (in-plane or out-plane) mode shapes are shown, and in these tables, numbers in parenthesis specify the mode numbers along x- and y-directions, and also bold-faced results indicate in-plane natural frequencies. Also, contour plots of the first three mode shapes of annular sector FG plates coupled with two piezoelectric layers with the SSSS boundary condition are illustrated in Fig. 11.
 |
 |
 |
|
| Fig. 11 First three in-plane mode shapes of annular sector FG plates coupled with two piezoelectric layers with SSSS boundary condition |
|
|
 |
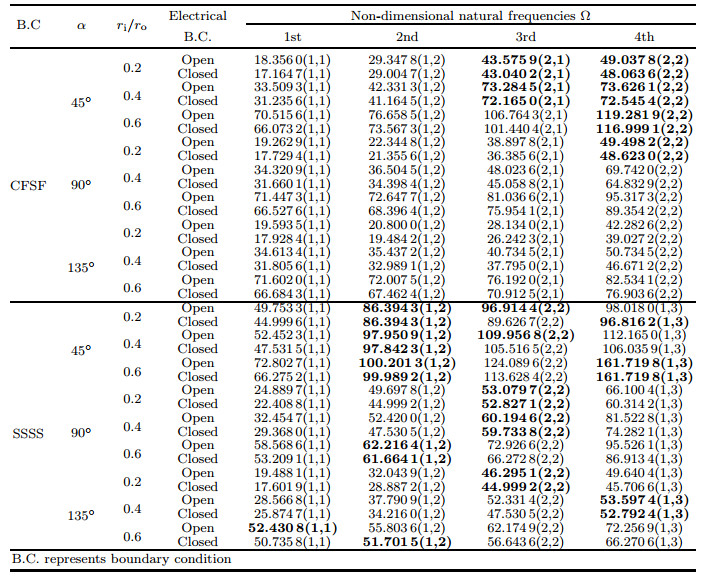 |
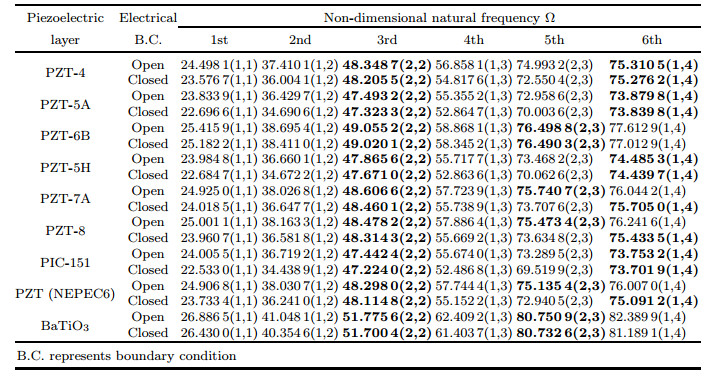
Table 8 presents the first six natural frequencies of an annularsector Al/Al2O3 plate with ri/ro=0.4, 2h/ro=0.08, n=1, and α =100° coupled with twopiezoelectric layers with hp/(2h)=0.15. In this table, the SSSS mechanical boundary condition and both open and closedcircuit electrical boundary conditions are considered. The effectsof different piezoelectric materials on in-plane and out-of-planenatural frequencies are shown in the aforementioned table.
The effects of angle α and the ratio of the inner radius to the outer radius ri/ro of an annular sector plate on in-plane and out-of-plane natural frequencies for two CFSF and SSSS boundary conditions are summarized in Table 9.
9 Summary and conclusionsIn this paper, the free vibration of annular sector FG plates embedded with two piezoelectric layers is studied using the GDQ method based on the FSD theory with different combinations of boundary conditions (clamped, simply supported, and free). Properties of the FG plate are assumed to vary according to the power distribution law of the volume fraction through the thickness. Both open and closed circuit (shortly connected) electrical boundary conditions on the piezoelectric surfaces, which are the electrical boundary conditions on sensors and actuators, respectively, are investigated. Electrical potentials on the surfaces of closed-circuit piezoelectric layers are zero. Therefore, when the plate vibrates, electric energy is released. On the other hand, because the surfaces of open circuit boundary condition are potentially insulated, this energy cannot be released and is converted into the mechanical energy. As a result, natural frequencies are increased. Two consequences of the larger piezoelectric layer thicknesses are increasing the stiffness of the structure and diminishing natural frequencies due to the piezoelectricity. The strength of these two stated phenomena leads to a decreasing-increasing trend in natural frequencies. Studying different piezoelectric materials indicates that PZT-5A and PZT-5H tend to diminish natural frequencies more than other piezoelectric materials investigated in this paper. In this study, in-plane modes of vibration are considered, and it is observed that, for a larger thickness of the plate, these modes appear in the lower modes of vibration. Omitting in-plane displacements could cause errors in calculations and lead to missing some modes in modal analysis of FG plates. This phenomenon plays a more critical role in smart FG plates. The effects of angle of sector plate, power law index in FGMs, the thicknesses of piezoelectric layers and FG plate, and plate geometrical parameters with different boundary conditions on the natural frequencies of the structure are presented in this paper for benchmark data.
| [1] |
TUTUNCU, N. and OZTURK, M. Exact solutions for stresses in functionally graded pressure vessels. Composites Part B:Engineering, 32, 683-686 (2001) |
| [2] |
JALALI, M. H., ZARGAR, O., and BAGHANI, M. Size-dependent vibration analysis of FG microbeams in thermal environment based on modified couple stress theory. Transactions of Mechanical Engineering (2018) doi:10.1007/s40997-018-0193-6 |
| [3] |
BAKHTIARI-NEJAD, F., SHAMSHIRSAZ, M., MOHAMMADZADEH, M., and SAMIE, S. Free vibration analysis of FG skew plates based on second order shear deformation theory. ASME 2014 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, American Society of Mechanical Engineers, New York (2014)
|
| [4] |
HASSANZADEH-AGHDAM, M. K., EDALATPANAH, S. A., and AZARIPOUR, S. Interphase region effect on the biaxial yielding envelope of SiC fiber-reinforced Ti matrix composites. Proceedings of the Institution of Mechanical Engineers, Part C:Journal of Mechanical Engineering Science, 0954406218777532 (2018) |
| [5] |
ZARGAR, O., MASOUMI, A., and MOGHADDAM, A. O. Investigation and optimization for the dynamical behaviour of the vehicle structure. International Journal of Automotive and Mechanical Engineering, 14, 4196-4210 (2017) doi:10.15282/ijame |
| [6] |
LIU, F. L. and LIEW, K. Free vibration analysis of Mindlin sector plates:numerical solutions by differential quadrature method. Computer Methods in Applied Mechanics and Engineering, 177, 77-92 (1999) doi:10.1016/S0045-7825(98)00376-4 |
| [7] |
WANG, X. and WANG, Y. Free vibration analyses of thin sector plates by the new version of differential quadrature method. Computer Methods in Applied Mechanics and Engineering, 193, 3957-3971 (2004) doi:10.1016/j.cma.2004.02.010 |
| [8] |
NIE, G. and ZHONG, Z. Vibration analysis of functionally graded annular sectorial plates with simply supported radial edges. Composite Structures, 84, 167-176 (2008) doi:10.1016/j.compstruct.2007.07.003 |
| [9] |
KELESHTERI, M., ASADI, H., and WANG, Q. Postbuckling analysis of smart FG-CNTRC annular sector plates with surface-bonded piezoelectric layers using generalized differential quadrature method. Computer Methods in Applied Mechanics and Engineering, 325, 689-710 (2017) doi:10.1016/j.cma.2017.07.036 |
| [10] |
KIANI, Y. and ESLAMI, M. An exact solution for thermal buckling of annular FGM plates on an elastic medium. Composites Part B:Engineering, 45, 101-110 (2013) doi:10.1016/j.compositesb.2012.09.034 |
| [11] |
HOSSEINI, R., ZARGAR, O., and HAMEDI, M. Improving power density of piezoelectric vibration-based energy scavengers. Journal of Solid Mechanics, 10, 98-109 (2018) |
| [12] |
JALALI, M. H., SHAHRIARI, B., ZARGAR, O., BAGHANI, M., and BANIASSADI, M. Free vibration analysis of rotating functionally graded annular disc of variable thickness using generalized differential quadrature method. Scientia Iranica, 25, 728-740 (2018) |
| [13] |
HAGHSHENAS, A. and ARANI, A. G. Nonlocal vibration of a piezoelectric polymeric nanoplate carrying nanoparticle via Mindlin plate theory. Proceedings of the Institution of Mechanical Engineers, Part C:Journal of Mechanical Engineering Science, 228, 907-920 (2014) doi:10.1177/0954406213491909 |
| [14] |
ARANI, A. G., HAGHSHENAS, A., AMIR, S., MOZDIANFARD, M. R., and LATIFI, M. Electrothermo-mechanical response of thick-walled piezoelectric cylinder reinforced by boron-nitride nanotubes. Strength of Materials, 45, 102-115 (2013) doi:10.1007/s11223-013-9437-2 |
| [15] |
WANG, Y., XU, R. Q., and DING, H. J. Free axisymmetric vibration of FGM circular plates. Applied Mathematics and Mechanics (English Edition), 30, 1077-1082 (2009) doi:10.1007/s10483-009-0901-x |
| [16] |
CHEN, W., LYU, C., and BIAN, Z. Free vibration analysis of generally laminated beams via state-space-based differential quadrature. Composite Structures, 63, 417-425 (2004) doi:10.1016/S0263-8223(03)00190-9 |
| [17] |
WANG, X. and LI, S. R. Free vibration analysis of functionally graded material beams based on Levinson beam theory. Applied Mathematics and Mechanics (English Edition), 37, 861-878 (2016) doi:10.1007/s10483-016-2094-9 |
| [18] |
SOHN, J. W., KIM, H. S., and CHOI, S. B. Active vibration control of smart hull structures using piezoelectric actuators. Proceedings of the Institution of Mechanical Engineers, Part C:Journal of Mechanical Engineering Science, 220, 1329-1337 (2006) doi:10.1243/09544062C06105 |
| [19] |
CHENG, G. M., GUO, K., ZENG, P., and SUN, Y. M. Development of a two-degree-of-freedom piezoelectric motor using single plate vibrator. Proceedings of the Institution of Mechanical Engineers, Part C:Journal of Mechanical Engineering Science, 226, 1036-1052 (2011) |
| [20] |
LI, F. M. and SONG, Z. G. Vibration analysis and active control of nearly periodic two-span beams with piezoelectric actuator/sensor pairs. Applied Mathematics and Mechanics (English Edition), 36, 279-292 (2015) doi:10.1007/s10483-015-1912-6 |
| [21] |
JAVANBAKHT, M., SHAKERI, M., and SADEGHI, S. N. Dynamic analysis of functionally graded shell with piezoelectric layers based on elasticity. Proceedings of the Institution of Mechanical Engineers, Part C:Journal of Mechanical Engineering Science, 223, 2039-2047 (2009) doi:10.1243/09544062JMES1309 |
| [22] |
AREFI, M., KARROUBI, R., and IRANI-RAHAGHI, M. Free vibration analysis of functionally graded laminated sandwich cylindrical shells integrated with piezoelectric layer. Applied Mathematics and Mechanics (English Edition), 37, 821-834 (2016) doi:10.1007/s10483-016-2098-9 |
| [23] |
MOHAMMADIMEHR, M. and ROSTAMI, R. Bending and vibration analyses of a rotating sandwich cylindrical shell considering nanocomposite core and piezoelectric layers subjected to thermal and magnetic fields. Applied Mathematics and Mechanics (English Edition), 39, 1-22 (2018) doi:10.1007/s10483-018-2301-6 |
| [24] |
WANG, Q., QUEK, S., SUN, C., and LIU, X. Analysis of piezoelectric coupled circular plate. Smart Materials and Structures, 10, 229-239 (2001) doi:10.1088/0964-1726/10/2/308 |
| [25] |
KELESHTERI, M., ASADI, H., and WANG, Q. Large amplitude vibration of FG-CNT reinforced composite annular plates with integrated piezoelectric layers on elastic foundation. Thin-Walled Structures, 120, 203-214 (2017) doi:10.1016/j.tws.2017.08.035 |
| [26] |
WU, N., WANG, Q., and QUEK, S. Free vibration analysis of piezoelectric coupled circular plate with open circuit. Journal of Sound and Vibration, 329, 1126-1136 (2010) doi:10.1016/j.jsv.2009.10.040 |
| [27] |
DUAN, W., QUEK, S. T., and WANG, Q. Free vibration analysis of piezoelectric coupled thin and thick annular plate. Journal of Sound and Vibration, 281, 119-139 (2005) doi:10.1016/j.jsv.2004.01.009 |
| [28] |
EBRAHIMI, F. and RASTGOO, A. An analytical study on the free vibration of smart circular thin FGM plate based on classical plate theory. Thin-Walled Structures, 46, 1402-1408 (2008) doi:10.1016/j.tws.2008.03.008 |
| [29] |
EBRAHIMI, F. and RASTGOO, A. Free vibration analysis of smart annular FGM plates integrated with piezoelectric layers. Smart Materials and Structures, 17, 015044 (2008) doi:10.1088/0964-1726/17/1/015044 |
| [30] |
HASHEMI, S. H., ES'HAGHI, M., and KARIMI, M. Closed-form vibration analysis of thick annular functionally graded plates with integrated piezoelectric layers. International Journal of Mechanical Sciences, 52, 410-428 (2010) |
| [31] |
PRAVEEN, G. and REDDY, J. Nonlinear transient thermoelastic analysis of functionally graded ceramic-metal plates. International Journal of Solids and Structures, 35, 4457-4476 (1998) doi:10.1016/S0020-7683(97)00253-9 |
| [32] |
REDDY, J. N. A simple higher-order theory for laminated composite plates. Journal of Applied Mechanics, 51, 745-752 (1984) doi:10.1115/1.3167719 |
| [33] |
MOHAMMADZADEH-KELESHTERI, M., ASADI, H., and AGHDAM, M. Geometrical nonlinear free vibration responses of FG-CNT reinforced composite annular sector plates integrated with piezoelectric layers. Composite Structures, 171, 100-112 (2017) doi:10.1016/j.compstruct.2017.01.048 |
| [34] |
LIU, X., WANG, Q., and QUEK, S. Analytical solution for free vibration of piezoelectric coupled moderately thick circular plates. International Journal of Solids and Structures, 39, 2129-2151 (2002) doi:10.1016/S0020-7683(02)00081-1 |
| [35] |
KELESHTERI, M., ASADI, H., and WANG, Q. On the snap-through instability of post-buckled FG-CNTRC rectangular plates with integrated piezoelectric layers. Computer Methods in Applied Mechanics and Engineering, 331, 53-71 (2018) doi:10.1016/j.cma.2017.11.015 |
| [36] |
MOHAMMADZADEH-KELESHTERI, M., SAMIE-ANARESTANI, S., and ASSADI, A. Large deformation analysis of single-crystalline nanoplates with cubic anisotropy. Acta Mechanica, 228, 3345-3368 (2017) doi:10.1007/s00707-017-1862-z |
| [37] |
MOHAMMADSALEHI, M., ZARGAR, O., and BAGHANI, M. Study of non-uniform viscoelastic nanoplates vibration based on nonlocal first-order shear deformation theory. Meccanica, 52, 1063-1077 (2017) doi:10.1007/s11012-016-0432-0 |
| [38] |
SHU, C. and DU, H. Implementation of clamped and simply supported boundary conditions in the GDQ free vibration analysis of beams and plates. International Journal of Solids and Structures, 34, 819-835 (1997) doi:10.1016/S0020-7683(96)00057-1 |
| [39] |
TORNABENE, F. and VIOLA, E. Vibration analysis of spherical structural elements using the GDQ method. Computers and Mathematics with Applications, 53, 1538-1560 (2007) doi:10.1016/j.camwa.2006.03.039 |
| [40] |
ZHAO, X., LEE, Y., and LIEW, K. M. Free vibration analysis of functionally graded plates using the element-free kp-Ritz method. Journal of Sound and Vibration, 319, 918-939 (2009) doi:10.1016/j.jsv.2008.06.025 |
| [41] |
HOSSEINI-HASHEMI, S., ES'HAGHI, M., and TAHER, H. R. D. An exact analytical solution for freely vibrating piezoelectric coupled circular/annular thick plates using Reddy plate theory. Composite Structures, 92, 1333-1351 (2010) doi:10.1016/j.compstruct.2009.11.006 |
| [42] |
FARSANGI, M. A., SAIDI, A., and BATRA, R. Analytical solution for free vibrations of moderately thick hybrid piezoelectric laminated plates. Journal of Sound and Vibration, 332, 5981-5998 (2013) doi:10.1016/j.jsv.2013.05.010 |
| [43] |
HASANI, S., SOLEYMANI, A. P., PANJEPOUR, M., and GHAEI, A. A tension analysis during oxidation of pure aluminum powder particles:non-isothermal condition. Oxidation of Metals, 82, 209-224 (2014) doi:10.1007/s11085-014-9488-1 |
| [44] |
LIEW, K. and LIU, F. L. Differential quadrature method for vibration analysis of shear deformable annular sector plates. Journal of Sound and Vibration, 230, 335-356 (2000) doi:10.1006/jsvi.1999.2623 |
| [45] |
FARSANGI, M.A. and SAIDI, A. Levy type solution for free vibration analysis of functionally graded rectangular plates with piezoelectric layers. Smart Materials and Structures, 21, 094017 (2012) doi:10.1088/0964-1726/21/9/094017 |

 2019, Vol. 40
2019, Vol. 40