Applied Mathematics and Mechanics (English Edition) ›› 2024, Vol. 45 ›› Issue (2): 277-294.doi: https://doi.org/10.1007/s10483-024-3076-8
• Articles • Previous Articles Next Articles
Jinlong LIU1, Di LU1,2, Bin CHEN3,4,*( )
)
Received:2023-11-03
Online:2024-02-01
Published:2024-01-27
Contact:
Bin CHEN
E-mail:chenb6@zju.edu.cn
Supported by:2010 MSC Number:
Jinlong LIU, Di LU, Bin CHEN. Tuning mechanical behaviors of highly entangled hydrogels with the random distribution of mobile entanglements. Applied Mathematics and Mechanics (English Edition), 2024, 45(2): 277-294.
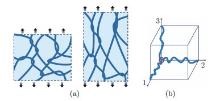
Fig. 1
(a) The schematic of a highly entangled hydrogel with dense entanglements, where entanglements within hydrogels function as mobile crosslinks, which can slide along polymer chains when hydrogels are subject to mechanical loading or water swelling; (b) the RVE of the hydrogel with dense entanglements, where there exists a chain segment along each edge of the cube and a mobile entanglement (red ring) at each corner of the cube (color online)"

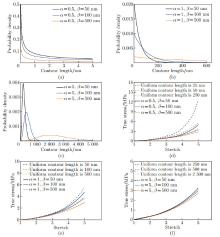
Fig. 2
(a)–(c) The effects of α or β in gamma distribution on the probability density of initial contour lengths of polymer chain segments within the gel; (d)–(f) theoretical predictions of stress-stretch curves of the corresponding gel. Predictions for the cases with uniform initial contour lengths are also plotted for comparison (color online)"

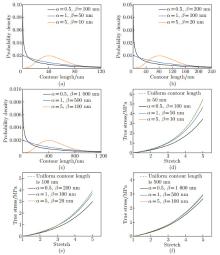
Fig. 3
(a)–(c) The effects of the product of αβ in gamma distribution on the probability density of initial contour lengths of polymer chain segments within hydrogels; (d)–(f) theoretical predictions of stress-stretch curves of hydrogels under uniaxial tension with varied distributions of entanglements within hydrogels. Predictions for the case with uniform initial contour lengths are also plotted for comparison (color online)"

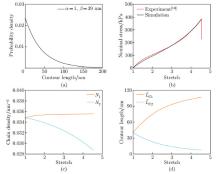
Fig. 4
(a) The predicted probability density of initial contour lengths of polymer chain segments within hydrogels; (b) the theoretical prediction of the stress-stretch curve agrees with the experimental results[10]; (c) the effective number of chain segments along the loading direction increases slowly while decreases rapidly along the perpendicular direction of the loading with stretch; (d) the average contour length along the loading direction increases and that perpendicular to the loading direction decreases with stretch. In the simulation, α=1, β=39 nm, the initial effective number of chain segments is 0.108 nm-3, and the stretch rate is 0.025 s-1 (color online)"
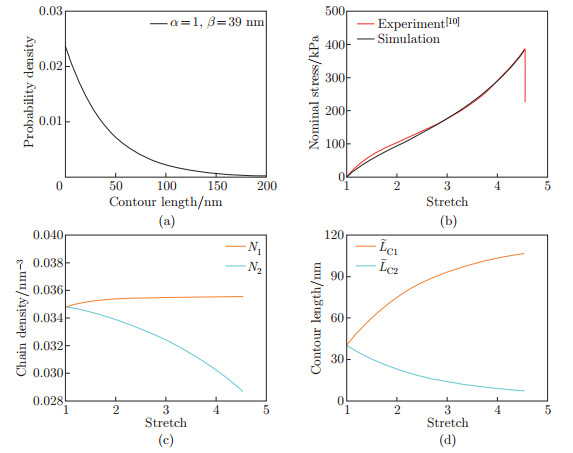
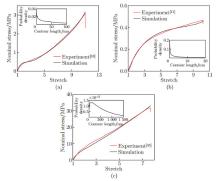
Fig. 5
Comparison of our model predictions with other experimental data: (a) the stress-stretch curve of a highly entangled elastomer under uniaxial tension[10], where in the analysis, N0=0.249 nm-3, α=0.7, β=128.57 nm, η=0.4 pN · s · nm-1, and χ=0.6; (b) the stress-stretch curve of a highly entangled hydrogel under uniaxial tension[11], where in the analysis, N0=0.075 nm-3, α=0.3, β=1 667 nm, η=11 pN · s · nm-1, Lcr=0.1 nm, and χ=0.45; (c) a stress-stretch curve of a highly entangled hydrogel under uniaxial tension[45], where in the analysis, N0=0.008 4 nm-3, α=1.2, β=500 nm, η=0.000 8 pN · s · nm-1, and χ=0.48 (color online)"
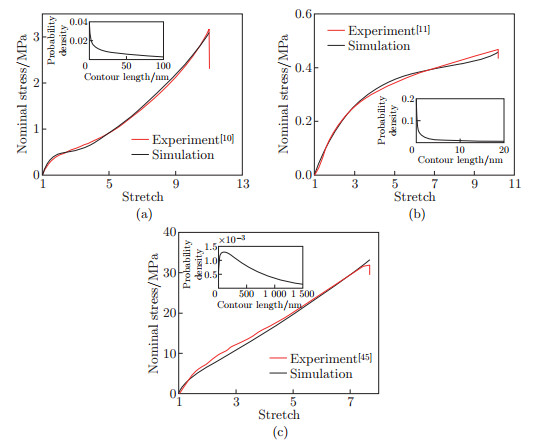
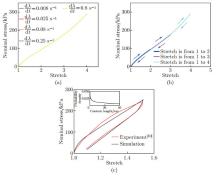
Fig. 6
(a) The prediction of the rate independence for the fully swollen highly entangled hydrogel, where in the analysis, η=0.000 1 pN · s · nm-1; (b) the prediction of the negligible hysteresis for the fully swollen highly entangled hydrogel, where arrows indicate loading or unloading, and η=0.000 1 pN · s · nm-1; (c) the prediction of the pronounced hysteresis for the as-prepared highly entangled hydrogel, where in the analysis, η=0.12 pN · s · nm-1 (color online)"
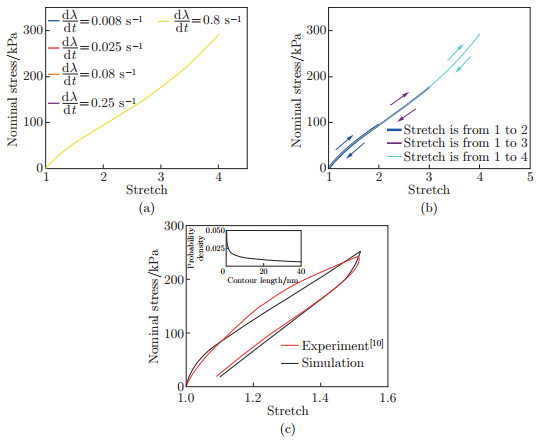
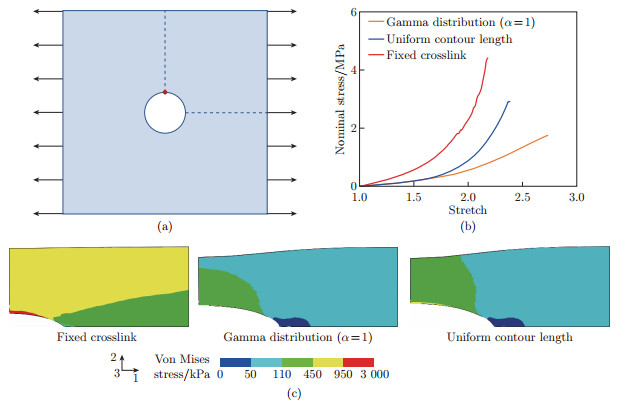
Fig. 7
Stresses in a plate with a circular hole existing at its center upon uniaxial tension, where three types of gel materials are under investigation, and the gel with fixed crosslinks is the stiffest, followed by the one with the uniform contour length, and then the one with the gamma distribution: (a) schematic of a square plate with a circular hole at its center subject to uniaxial tension; (b) the maximum of the nominal stress, σ11, within the plate changes with stretch; (c) stress contours at a stretch ratio of 2. In the simulations, the initial contour length of the chain segments within the RVE is 39 nm, the number density of chain segments is 0.108 nm-3, the stretch rate is 0.1 s-1, the critical value of the contour length for the case with the uniform contour length is 0, and other parameters are listed in Table 1 by default. For the case of fixed crosslinks, the frictional coefficient is set to be a very large value, which is 10 000 pN · s · nm-1 (color online)"
| 1 | GUO,X.,DONG,X. Y.,ZOU,G. J.,GAO,H. J., andZHAI,W.Strong and tough fibrous hydrogels reinforced by multiscale hierarchical structures with multimechanisms.Science Advances,9(2),eadf7075(2023) |
| 2 | HUA,M. T.,WU,S. W.,MA,Y. F.,ZHAO,Y. S.,CHEN,Z. L.,FRENKEL,I.,STRZALKA,J.,ZHOU,H.,ZHU,X. Y., andHE,X. M.Strong tough hydrogels via the synergy of freeze-casting and salting out.nature,590(7847),594-599(2021) |
| 3 | LIU,C.,MORIMOTO,N.,JIANG,L.,KAWAHARA,S.,NORITOMI,T.,YOKOYAMA,H.,MAYUMI,K., andITO,K.Tough hydrogels with rapid self-reinforcement.Science,372(6546),1078-1081(2021) |
| 4 | NIAN,G. D.,KIM,J.,BAO,X. Y., andSUO,Z. G.Making highly elastic and tough hydrogels from doughs.Advanced Materials,34(50),2206577(2022) |
| 5 | WANG,Z.,ZHENG,X. J.,OUCHI,T.,KOUZNETSOVA,T. B.,BEECH,H. K.,AV-RON,S.,MATSUDA,T.,BOWSER,B. H.,WANG,S.,JOHNSON,J. A.,KALOW,J. A.,OLSEN,B. D.,GONG,J. P.,RUBINSTEIN,M., andCRAIG,S. L.Toughening hydrogels through force-triggered chemical reactions that lengthen polymer strands.Science,374(6564),193-196(2021) |
| 6 | ZHAO,X. H.,CHEN,X. Y.,YUK,H.,LIN,S. T.,LIU,X. Y., andPARADA,G.Soft materials by design: unconventional polymer networks give extreme properties.Chemical Reviews,121(8),4309-4372(2021) |
| 7 | HAN,S. J.,WU,Q. R.,ZHU,J. D.,ZHANG,J. Y.,CHEN,A. B.,SU,S.,LIU,J. T.,HUANG,J. R.,YANG,X. X., andGUAN,L. H.Tough hydrogel with high water content and ordered fibrous structures as an artificial human ligament.Materials Horizons,10(3),1012-1019(2023) |
| 8 | GONG,J. P.,KATSUYAMA,Y.,KUROKAWA,T., andOSADA,Y.Double-network hydrogels with extremely high mechanical strength.Advanced Materials,15(14),1155-1158(2003) |
| 9 | JIA,Y. T.,ZHOU,Z. D.,JIANG,H. L., andLIU,Z. S.Characterization of fracture toughness and damage zone of double network hydrogels.Journal of the Mechanics and Physics of Solids,169,105090(2022) |
| 10 | KIM,J.,ZHANG,G. G.,SHI,M. X. Z., andSUO,Z. G.Fracture, fatigue, and friction of polymers in which entanglements greatly outnumber cross-links.Science,374(6564),212-216(2021) |
| 11 | LI,D. K.,ZHAN,W.,ZUO,W.,LI,L. P.,ZHANG,J.,CAI,G. Y., andTIAN,Y.Elastic, tough and switchable swelling hydrogels with high entanglements and low crosslinks for water remediation.Chemical Engineering Journal,450,138417(2022) |
| 12 | LIU,P. Y.,ZHANG,Y.,GUAN,Y., andZHANG,Y. J.Peptide-crosslinked, highly entangled hydrogels with excellent mechanical properties but ultra-low solid content.Advanced Materials,35(13),2210021(2023) |
| 13 | SHI,M. X. Z.,KIM,J.,NIAN,G. D., andSUO,Z. G.Highly entangled hydrogels with degradable crosslinks.Extreme Mechanics Letters,59,101953(2023) |
| 14 | WANG,Y. C.,NIAN,G. D.,KIM,J., andSUO,Z. G.Polyacrylamide hydrogels VI: synthesis-property relation.Journal of the Mechanics and Physics of Solids,170,105099(2023) |
| 15 | TANI,J.,TAKAGI,T., andQIU,J.Intelligent material systems: application of functional materials.Applied Mechanics Reviews,51(8),505-521(1998) |
| 16 | BOSNJAK,N., andSILBERSTEIN,M. N.Pathways to tough yet soft materials.Science,374(6564),150-151(2021) |
| 17 | BUKOWSKI,C.,ZHANG,T.,RIGGLEMAN,R. A., andCROSBY,A. J.Load-bearing entanglements in polymer glasses.Science Advances,7(38),eabg9763(2021) |
| 18 | ZHU,J. K., andLUO,J.Effects of entanglements and finite extensibility of polymer chains on the mechanical behavior of hydrogels.Acta Mechanica,229,1703-1719(2018) |
| 19 | EDWARDS,S. F., andVILGIS,T.The effect of entanglements in rubber elasticity.Polymer,27(4),483-492(1986) |
| 20 | NIAN,X. C.,YANG,Q. S.,MA,L. H., andZHANG,X. Y.Constitutive modeling for hydrogel with chain entanglements and application to adaptive hydrogel composite structures.Mechanics of Advanced Materials and Structures,30(24),5122-5136(2023) |
| 21 | BAYAT,M. R.,DOLATABADI,R., andBAGHANI,M.Transient swelling response of ph-sensitive hydrogels: a monophasic constitutive model and numerical implementation.International Journal of Pharmaceutics,577,119030(2020) |
| 22 | BÖGER,L.,NATEGHI,A., andMIEHE,C.A minimization principle for deformation-diffusion processes in polymeric hydrogels: constitutive modeling and FE implementation.International Journal of Solids and Structures,121,257-274(2017) |
| 23 | MENG,Q. H., andSHI,X. H.A mechanistically motivated constitutive model of biopolymer hydrogels with structural evolution.Journal of the Mechanics and Physics of Solids,173,105205(2023) |
| 24 | HUANG,R.,ZHENG,S. J.,LIU,Z. S., andNG,T. Y.Recent advances of the constitutive models of smart materials — hydrogels and shape memory polymers.International Journal of Applied Mechanics,12(2),2050014(2020) |
| 25 | PAN,Z. Z., andBRASSART,L.Constitutive modelling of hydrolytic degradation in hydrogels.Journal of the Mechanics and Physics of Solids,167,105016(2022) |
| 26 | WANG,Q. M., andGAO,Z. M.A constitutive model of nanocomposite hydrogels with nanoparticle crosslinkers.Journal of the Mechanics and Physics of Solids,94,127-147(2016) |
| 27 | DAL,H.,AÇIKGÖZ,K., andBADIENIA,Y.On the performance of isotropic hyperelastic constitutive models for rubber-like materials: a state of the art review.Applied Mechanics Reviews,73(2),020802(2021) |
| 28 | LU,D., andCHEN,B.A constitutive theory for large stretch behaviors of slide-ring gels by considering molecular frictions.Soft Matter,19(8),1531-1539(2023) |
| 29 | FALENDER,J. R.,YEH,G. S. Y., andMARK,J. E.The effect of chain length distribution on elastomeric properties 1: comparisons between random and highly nonrandom networks.Journal of the American Chemical Society,101(24),7353-7356(1979) |
| 30 | LI,B., andBOUKLAS,N.A variational phase-field model for brittle fracture in polydisperse elastomer networks.International Journal of Solids and Structures,182-183,193-204(2020) |
| 31 | DARGAZANY,R., andITSKOV,M.A network evolution model for the anisotropic Mullins effect in carbon black filled rubbers.International Journal of Solids and Structures,46(16),2967-2977(2009) |
| 32 | ZHANG,H. H., andHU,Y. H.A statistical-chain-based theory for dynamic living polymeric gels with concurrent diffusion, chain remodeling reactions and deformation.Journal of the Mechanics and Physics of Solids,172,105155(2023) |
| 33 | GHAREEB,A., andELBANNA,A.An adaptive quasicontinuum approach for modeling fracture in networked materials: application to modeling of polymer networks.Journal of the Mechanics and Physics of Solids,137,103819(2020) |
| 34 | LAVOIE,S. R.,LONG,R., andTANG,T.Modeling the mechanics of polymer chains with deformable and active bonds.The Journal of Physical Chemistry B,124(1),253-265(2020) |
| 35 | WANG,Q. M.,GOSSWEILER,G. R.,CRAIG,S. L., andZHAO,X. H.Mechanics of mechanochemically responsive elastomers.Journal of the Mechanics and Physics of Solids,82,320-344(2015) |
| 36 | GUO,Q., andZAÏRI,F.A micromechanics-based model for deformation-induced damage and failure in elastomeric media.International Journal of Plasticity,140,102976(2021) |
| 37 | LU,T. Q.,WANG,Z. T.,TANG,J. D.,ZHANG,W. L., andWANG,T. J.A pseudo-elasticity theory to model the strain-softening behavior of tough hydrogels.Journal of the Mechanics and Physics of Solids,137,103832(2020) |
| 38 | ITSKOV,M., andKNYAZEVA,A.A rubber elasticity and softening model based on chain length statistics.International Journal of Solids and Structures,80,512-519(2016) |
| 39 | YASUDA,Y.,MASUMOTO,T.,MAYUMI,K.,TODA,M.,YOKOYAMA,H.,MORITA,H., andITO,K.Molecular dynamics simulation and theoretical model of elasticity in slide-ring gels.ACS Macro Letters,9(9),1280-1285(2020) |
| 40 | TRELOAR,L. R. G.The elasticity and related properties of rubbers.Reports on Progress in Physics,36(7),755(1973) |
| 41 | CAI,S. Q., andSUO,Z. G.Mechanics and chemical thermodynamics of phase transition in temperature-sensitive hydrogels.Journal of the Mechanics and Physics of Solids,59(11),2259-2278(2011) |
| 42 | MARKO,J. F., andSIGGIA,E. D.Statistical mechanics of supercoiled DNA.Physical Review E,52(3),2912-2938(1995) |
| 43 | EPSTEIN,M., andSEGEV,R.Differentiable manifolds and the principle of virtual work in continuum mechanics.Journal of Mathematical Physics,21(5),1243-1245(2008) |
| 44 | LÁNCZOS, C. The Variational Principles of Mechanics, Courier Corporation, U. S. A. (2012) |
| 45 | NORIOKA,C.,INAMOTO,Y.,HAJIME,C.,KAWAMURA,A., andMIYATA,T.A universal method to easily design tough and stretchable hydrogels.NPG Asia Materials,13(1),34(2021) |
| 46 | JAMES,H. M., andGUTH,E.Theory of the elastic properties of rubber.The Journal of Chemical Physics,11(10),455-481(1943) |
| 47 | ARRUDA,E. M., andBOYCE,M. C.A three-dimensional constitutive model for the large stretch behavior of rubber elastic materials.Journal of the Mechanics and Physics of Solids,41(2),389-412(1993) |
| 48 | FAN,Q. Y.,CHEN,B., andCAO,Y.Constitutive model reveals the defect-dependent viscoelasticity of protein hydrogels.Journal of the Mechanics and Physics of Solids,125,653-665(2019) |
| [1] | ZHANG Yun;HUANG Zhu-ping . MECHANICAL BEHAVIOR OF AMORPHOUS POLYMERS IN SHEAR [J]. Applied Mathematics and Mechanics (English Edition), 2004, 25(10): 1089-1099. |
| [2] | WANG Biao;XIAO Zhong-min. GENERAL CONSTITUTIVE EQUATIONS OF AN ER SUSPENSION BASED ON THE INTERNAL VARIABLE THEORY [J]. Applied Mathematics and Mechanics (English Edition), 2001, 22(2): 190-209. |
| Viewed | ||||||
|
Full text |
|
|||||
|
Abstract |
|
|||||


 Email Alert
Email Alert RSS
RSS