Fig. 1

Schematic diagrams demonstrating equivalence of wave boundary layer and oscillatory boundary layer (color online)"

Fig. 2

Schematic diagram of definition of forward-leaning degree for forward-leaning waves (color online)"

Table 1

Parameters of experimental data"

Fig. 3

Regime diagram of oscillatory flow over rough wall[30] (color online)"

Fig. 4

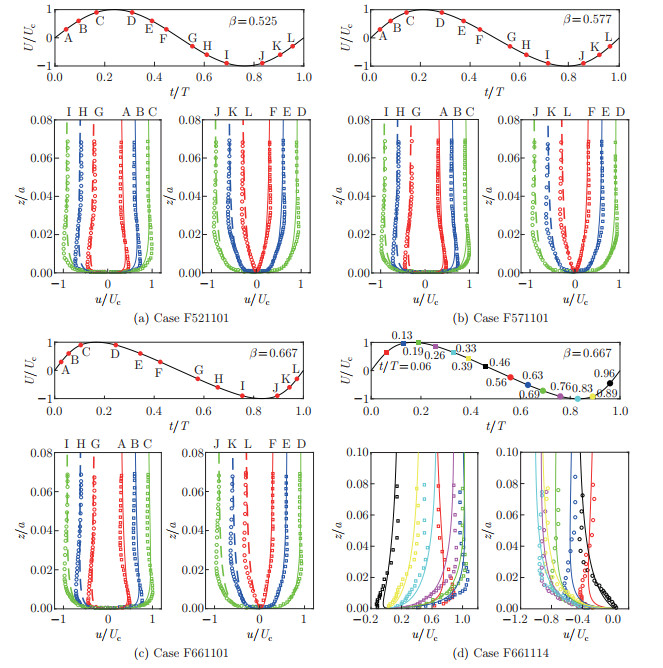
Comparisons of velocity profile at different phases calculated by Eq. (13) and experimental data of Ref. [35], where squares and circles denote experimental data, lines are analytical results, colors in (a)-(c) correspond to |U|/Uc=0.3 (red), |U|/Uc=0.6 (blue), and |U|/Uc=0.9 (green), and colors in (d) represent the phases as indicated by the same colors in the upper panel (color online)"

Fig. 5

Comparisons of velocity profile at different phases between Eq. (13) and experimental data of Ref. [37], where circles denote experimental data, lines are present analytical results, and colors represent phases (color online)"

Fig. 6

Comparisons of velocity profile at different phases calculated by Eq. (13) and experimental data of Ref. [5], where squares denote experimental data, lines are present analytical results, and colors represent phases (color online)"

Fig. 7

Comparisons of near-bed orbital velocity outside boundary layer of sinusoidal wave and experimental data of Ref. [5](color online)"

Fig. 8

Comparisons of velocity profile at different phases between Eq. (13) and experimental data of Ref. [25], where diamonds denote experimental data, lines are analytical results, and colors represent phases (color online)"

Fig. 9

Comparisons of velocity profile at different phases between Eq. (13) and experimental data of Ref. [36], where circles denote experimental data, lines are analytical results, and colors represent 8 phases evenly distributed through cycle (color online)"

Fig. 10

Comparisons of periodic velocity profile between Eq. (13) and experimental data, where circles denote experimental data, and lines are analytical results (color online)"

Table 2

Errors between analytical velocity calculated by Eq. (13) and experimental data"

Table 3

Errors between analytical bottom shear stress calculated by Eq. (15) and experimental data"

Fig. 11

Comparisons of periodic bottom shear stress calculated by Eq. (15) and experimental data of Ref. [5] (color online)"

Fig. 12

Comparisons of periodic bottom shear stress calculated by Eq. (15) and experimental data of Ref. [35] (color online)"

Fig. 13

Comparisons of near-bed orbital velocity outside boundary layer calculated by Eq. (18) and experimental data of Ref. [35] (color online)"

Fig. 14

Comparisons of periodic bottom shear stress calculated by Eq. (15) and experimental data of Ref. [38] (color online)"