Fig. 1

Diagram of 3 × 3 cables with (a) identical (ζ=1) and (b) opposite (ζ=-1) chiralities"

Fig. 2

Illustration of homogenized triplets for 3 × 3 cables: (a) cross-section of wires; (b) homogenization of strands (color online)"

Fig. 3

(a) Diagram of the wire internal forces. (b) Strand (triplet) in a 3 × 3 double-helix cable. (c) Internal forces and moments in the homogenized strand (color online)"

Fig. 4

Diagram of the level-N cable geometric parameters (a) before and (b) after deformation (color online)"

Fig. 5

Diagram of bending deformation of single strand under bending moments"

Fig. 6

Schematic representation of the numerical implementation of the mode (color online)"

Fig. 7

Prediction of the overall axial force from the axial displacement of a 3 × 3 CICC cable (color online)"

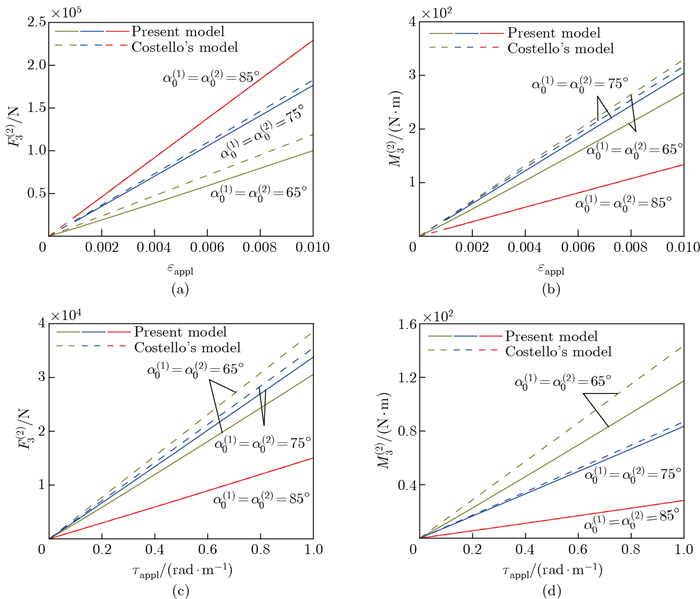
Fig. 8

Overall axial force and moment in the 3 × 3 cable subjected to external axial loading for different helical angles: (a) axial force F3(2) versus εappl; (b) axial twisting moment M3(2) versus εappl; (c) axial force F3(2) versus τappl; (d) axial twisting moment M3(2) versus τappl (color online)"

Fig. 9

Stiffness components varying with the helical angle: (a) kεε, (b) kεθ, (c) kθε, and (d) kθθ (color online)"

Fig. 10

Contact displacements varying with the helical angle subjected to (a) different axial strains εappl and (b) different twisting moments τappl (color online)"

Fig. 11

Stiffness components varying with the helical angles (α0(1) ≠ α0(2)): (a) kε ε, (b) kεθ, (c) kθε, and (d) kθθ (color online)"

Fig. 12

Dimensionless axial stress σ3, max(0) of the wire varying with external loadings for different helical angles: (a) axial tensile strain εappl and (b) axial torsion τappl (color online)"

Fig. 13

Dimensionless axial stress σ3, max(0) varying with the helical angle α0(1) at several representative values of α0(2) when (a) the external torsion τappl is zero and (b) the axial tensile strain εappl is zero (color online)"

Fig. 14

Dimensionless ${\bar M}$3(0) varying with the helical angle α0(1) when (a) the external torsion τappl is zero, and (b) the axial tensile strain εappl is zero (color online)"

Fig. 15

Dimensionless axial stress σ3, max(0) varying with the helical angle when (a) the external torsion τappl is zero, and (b) the axial tensile strain εappl is zero (color online)"

Fig. 16

Dimensionless axial stress σ3, max(0) dependence on the helical angles α0(1) and α0(2) under uniaxial tension: (a) identical (ζ =1) and (b) opposite (ζ =-1) (color online)"

Fig. 17

Dimensionless axial stress σ3, max(0) varying with the helical angles α0(1) and α0(2) under uniaxial torsion: (a) identical (ζ =1) and (b) opposite (ζ =-1) (color online)"