Fig. 1

Two examples of the oscillation patterns showing sliding motions[23]. Simulations of the system (1) with the frequency ratio $ n=2 $ for different values of the frequency-switching threshold $ a $. (a) $ a=0.7 $; (b) $ a=0.4 $. The other parameters are fixed at $ \delta=0.5 $, $ \beta=0.5 $, and $ \omega=0.01 $ (color online)"

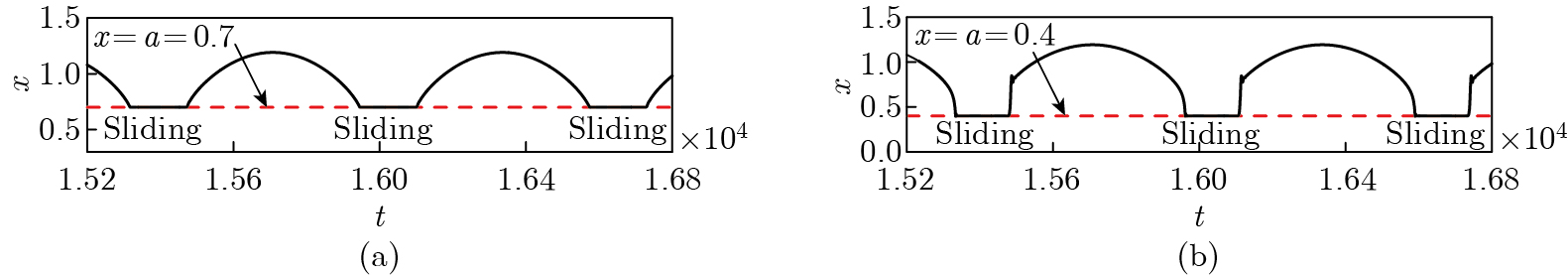
Fig. 2

Generation of mixed-mode fast-slow oscillations in the system (1) with $ a=0.7 $ for different values of $ n $. (a) $ n=3 $; (b) $ n=11 $; (c) $ n=19 $; (d) $ n=27 $. The other parameters are the same as in Fig. 1. The red numbers 1, 3, 5, and 7 mean the numbers of large-amplitude oscillations of relaxational type. Here, the oscillation pattern in Fig. 1(a) for the case $ n=2 $, denoted by the red dashed curve, is overlaid (color online)"

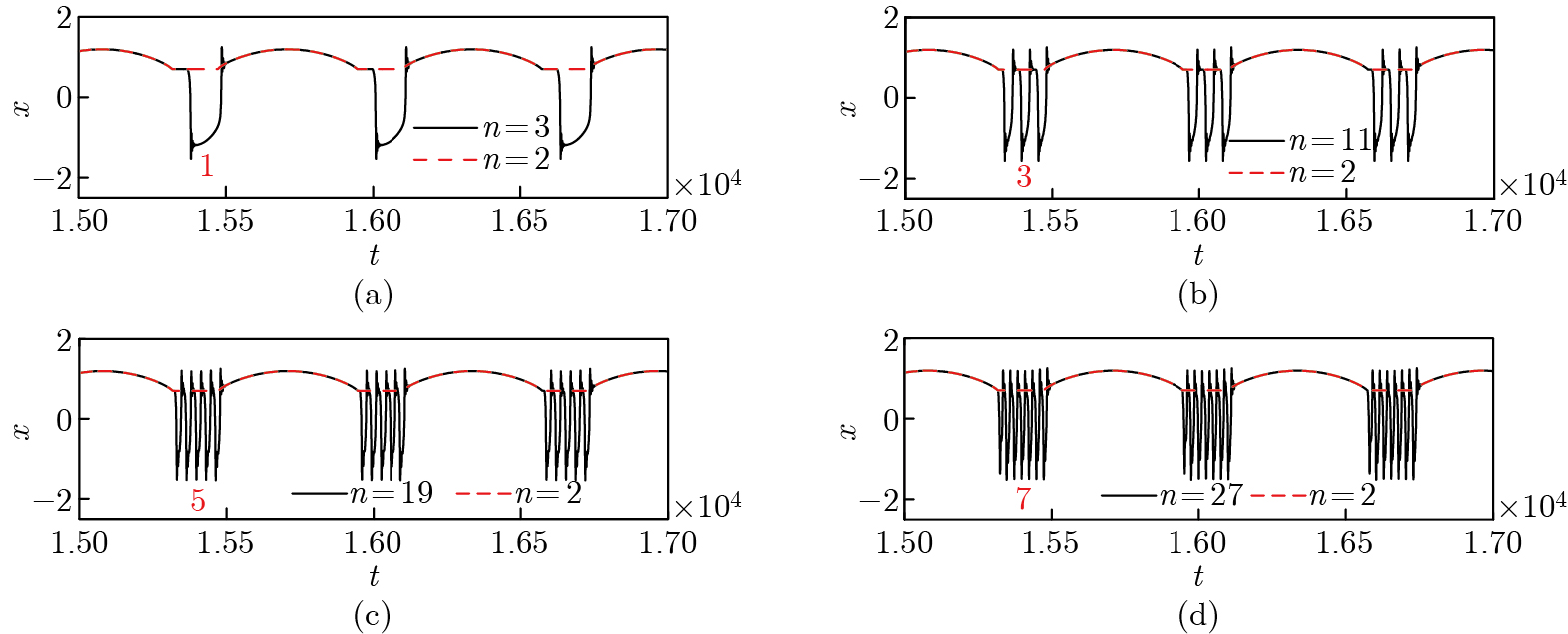
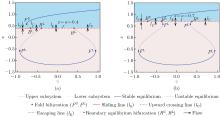
Fig. 3

Bifurcation behaviors of the system (3) with respect to $ \gamma $ for different values of $ a $[23]. (a) $ a=0.4 $; (b) $ a=0.7 $. The other parameters are the same as in Fig. 1. Sliding line (escaping line): both of the neighboring vector fields point towards (depart from) the boundary; upward crossing line: both of the neighboring vector fields show flows with the upward direction. Throughout this paper, the superscript characters U and L in the symbols (e.g., $ B^{\rm U} $ and $ F^{\rm L} $) mean something related to the upper and lower subsystems, respectively (color online)"

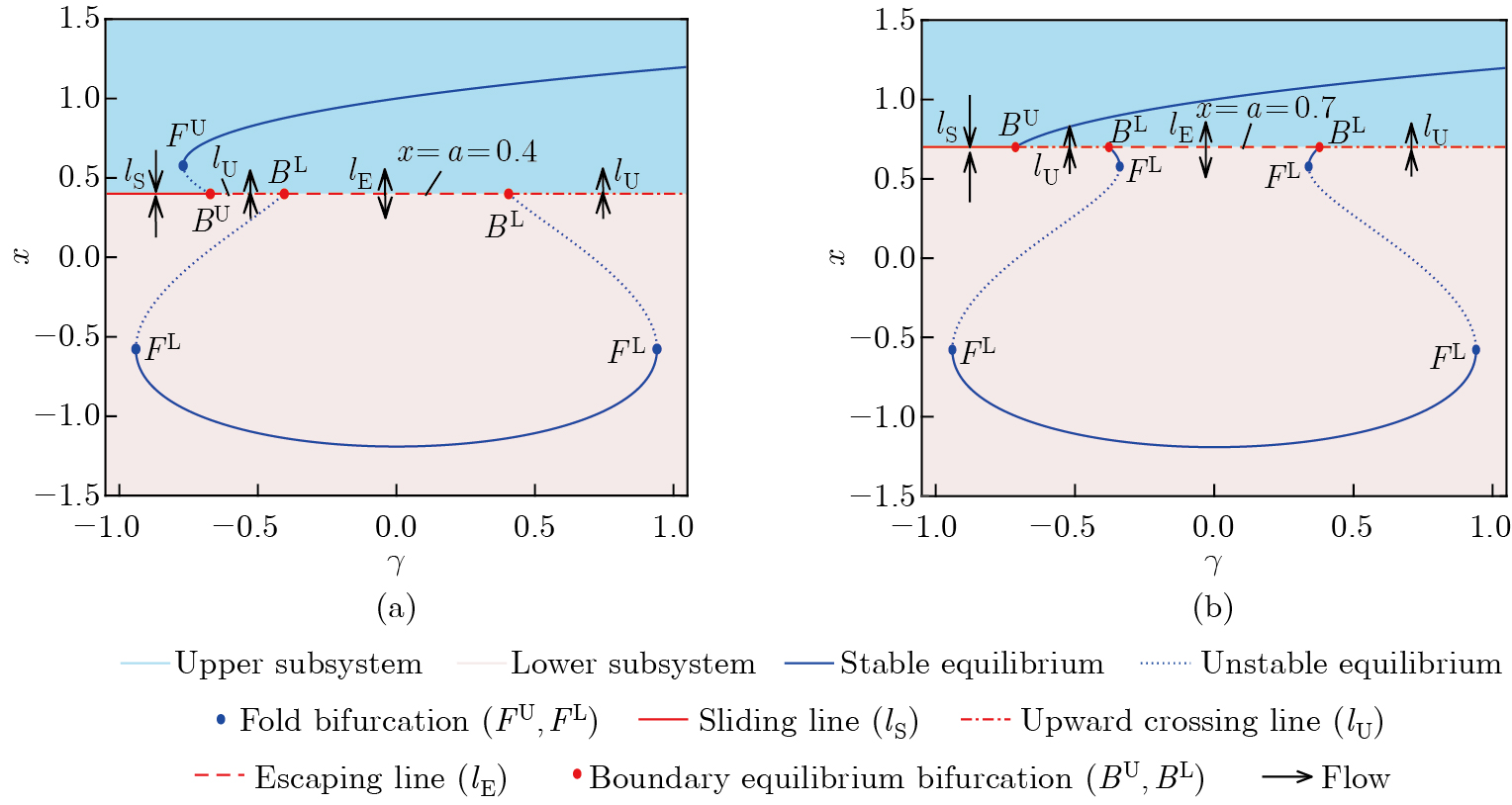
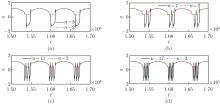
Fig. 4

Typical fast-slow oscillation patterns for the case $ 0<a<a_{\rm c} $. (a) $ n=3 $; (b) $ n=7 $; (c) $ n=11 $; (d) $ n=17 $. Here, $ a=0.4 $, and $ \delta $, $ \beta $, and $ \omega $ are the same as in Fig. 2. The red dashed curve is the oscillation pattern for $ n=2 $ in Fig. 1(b) (color online)"

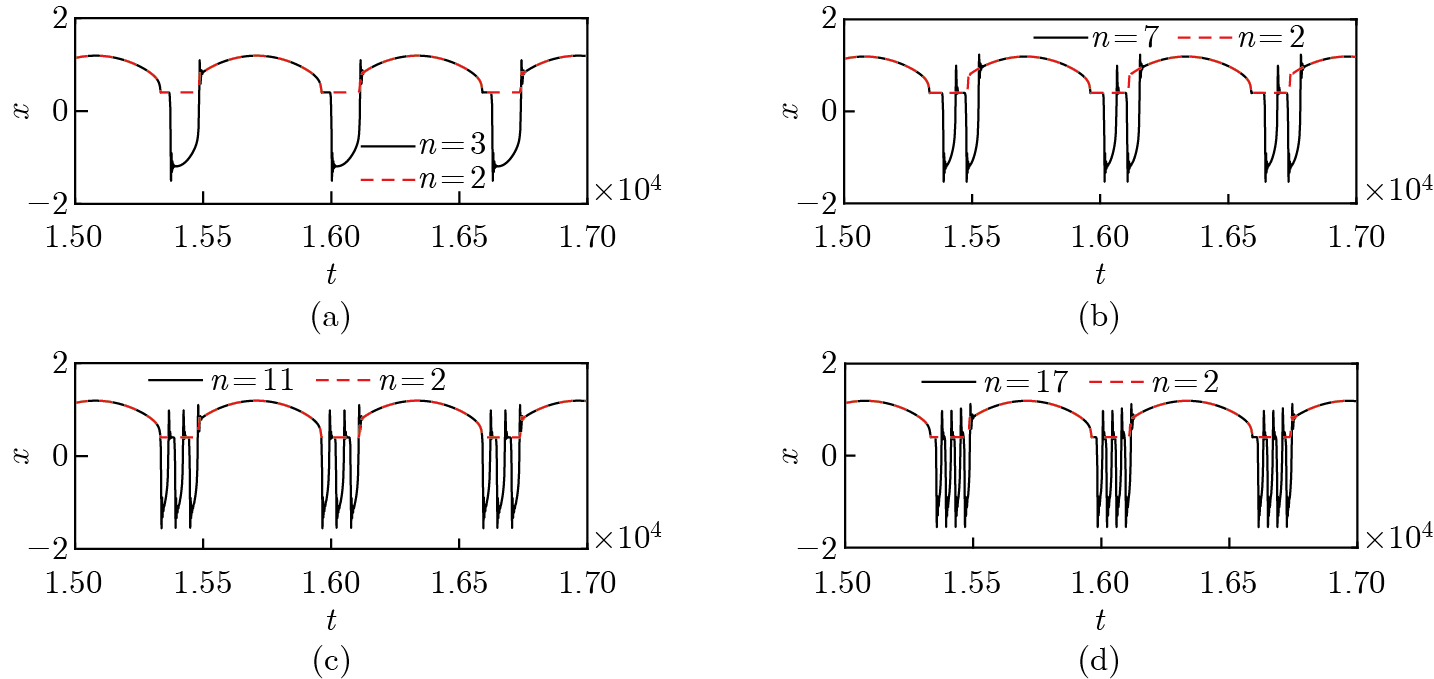
Fig. 5

Typical one-parameter bifurcation behaviors of the two subsystems in a whole range of $ x $ with respect to $ \gamma $. (a) The case related to the upper subsystem (5a); (b) and (c) the cases related to the lower subsystem (5b) for different values of $ n $, i.e., (b) $ n=3 $ and (c) $ n=7 $. In (a)–(c), the system parameters are the same as in Fig. 2 (color online)"

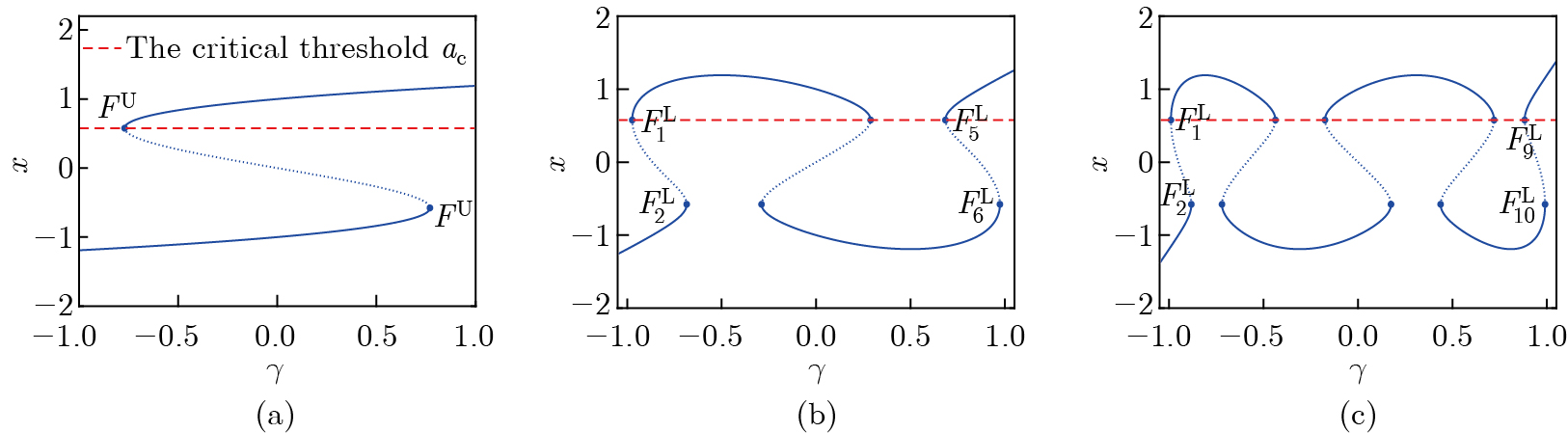
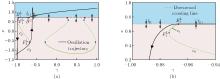
Fig. 6

Fast-slow analysis of the oscillation pattern in Fig. 2(a) (i.e., the case when $ n=3 $). (a) Overlay of the transformed phase diagram of the oscillation pattern in Fig. 2(a) with the bifurcation behaviors of the system (5) with respect to $ \gamma $; (b) the local enlargement of (a). Here, the equilibrium branches are highlighted with thick green curves (color online)"

Fig. 7

Fast-slow analysis of the oscillation pattern for the case when $ n=5 $. The other parameters are the same as in Fig. 6. Here, (b) is the local enlargement of (a). (a) and (c) show the phase and the time series of the oscillation pattern, respectively (color online)"

Fig. 8

Fast-slow analysis of the oscillation pattern in Fig. 2(b), i.e., the case when $ n=11 $. Here, (b) is the local enlargement of (a) (color online)"

Fig. 9

Bifurcation analysis of the system (5) for the cases when (a) $ n=19 $ and (b) $ n=27 $. Here, only the first and the last groups of the bifurcations, related to the generation of the clusters, are labeled (color online)"

Fig. 10

Fast-slow analysis of the oscillation pattern in Fig. 4(a), i.e., the case when $ a=0.4 $ and $ n=3 $. Here, (b) is the local enlargement of (a) (color online)"

Fig. 11

Fast-slow analysis of the oscillation pattern in Fig. 4(b), i.e., the case when $ a=0.4 $ and $ n=7 $. Here, (b) is the local enlargement of (a) (color online)"

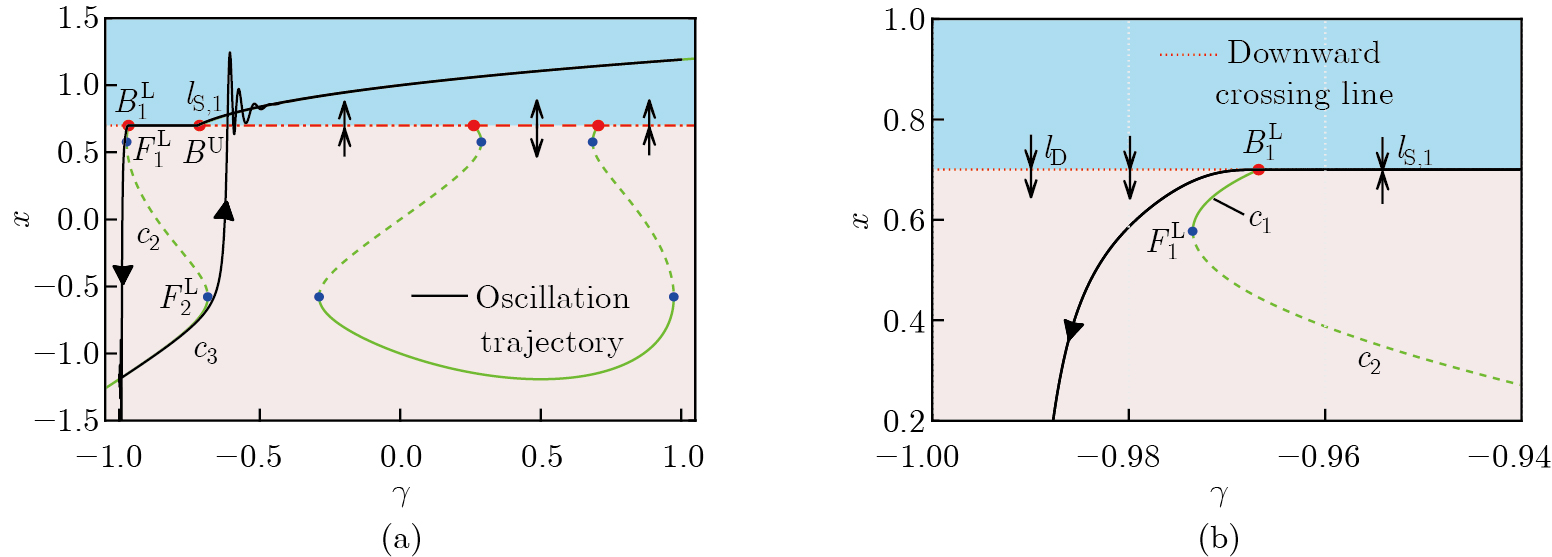
Fig. 12

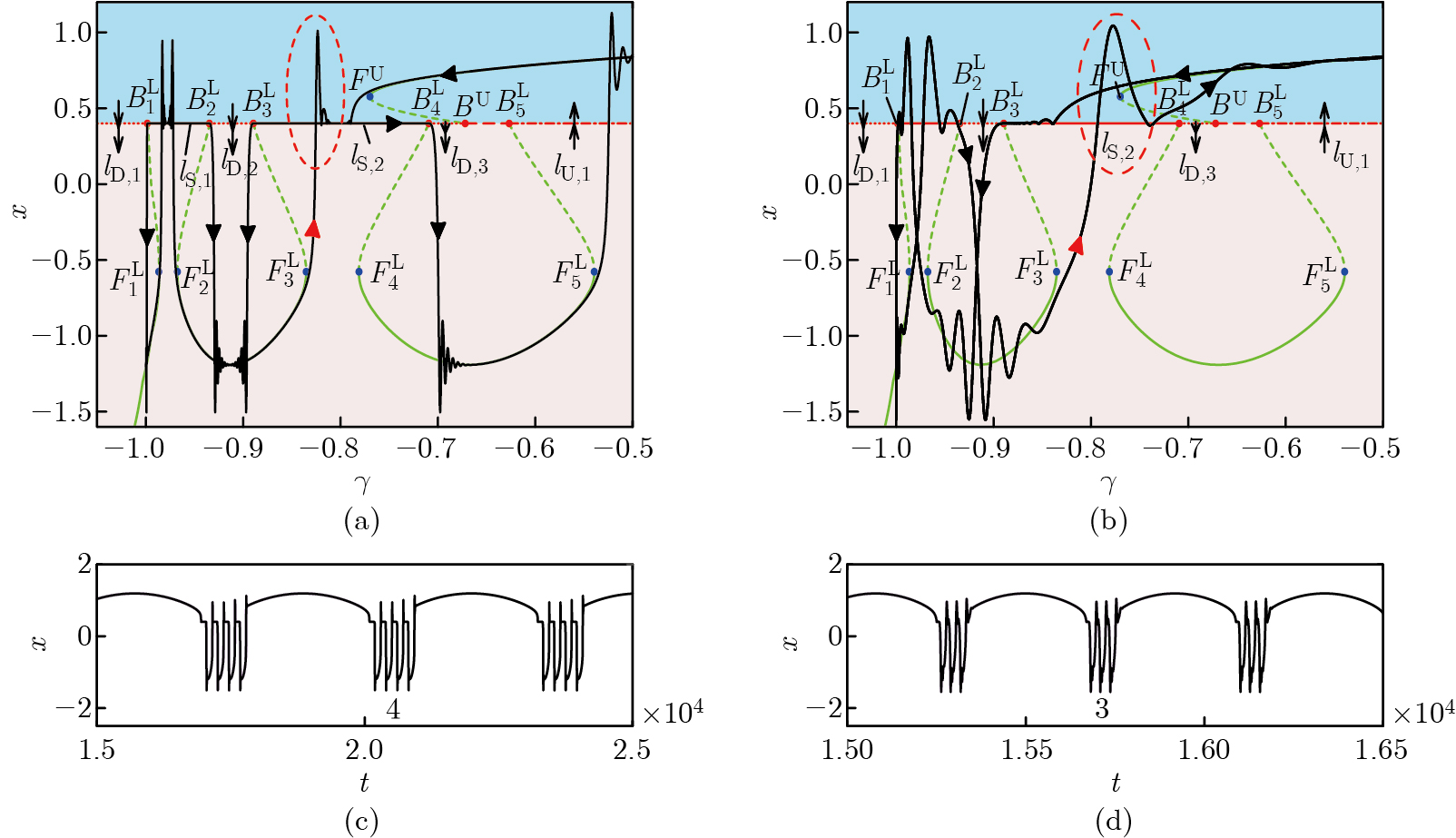
Fast-slow analysis of the oscillation pattern in Fig. 4(c), i.e., the case when $ a=0.4 $ and $ n=11 $. (a) Bifurcation diagram of the system (5) with respect to $ \gamma $; (b) overlay of the bifurcation diagram in (a) with the transformed phase diagram of the oscillation pattern in Fig. 4(c). Here, only the bifurcations and transition properties associated with the generation of the clusters are presented (color online)"

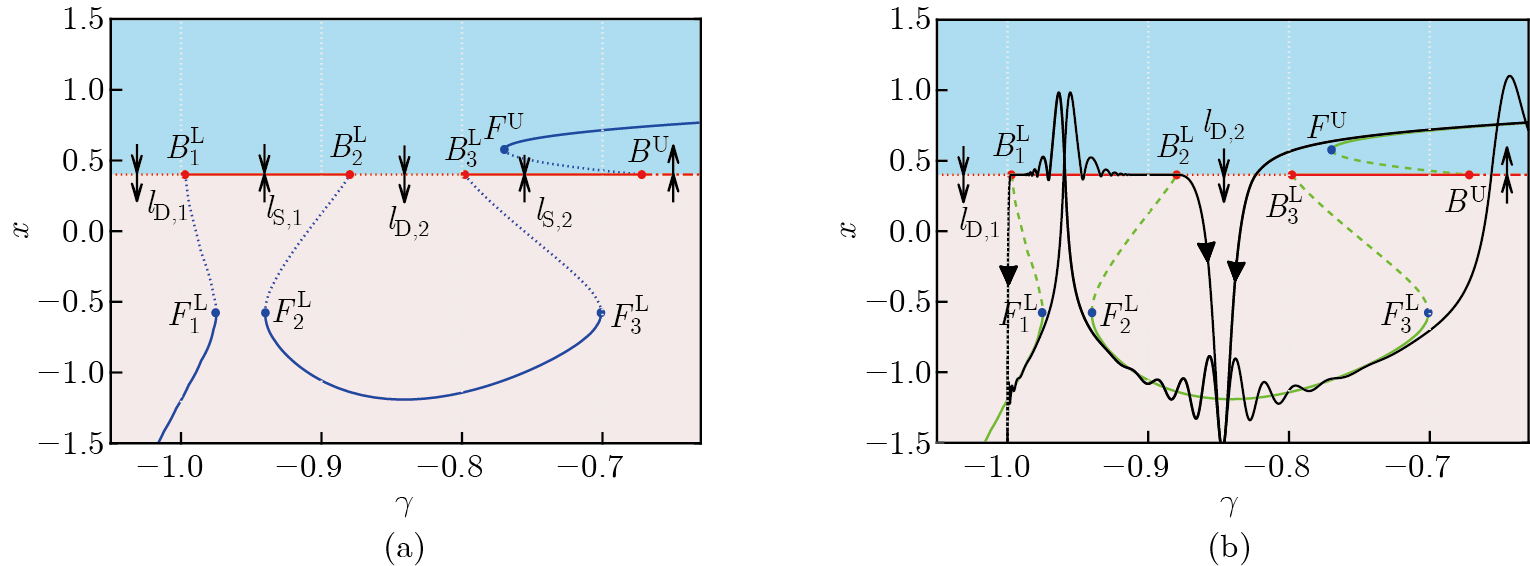
Fig. 13

Mixed-mode fast-slow oscillations for different values of $ \omega $ showing different dynamical characteristics. (a) and (c) the case related to $ \omega=0.002 $, showing four large-amplitude oscillations in the clusters; (b) and (d) the case related to $ \omega=0.015 $, exhibiting three large-amplitude oscillations in the clusters. Here, the stability and bifurcation behaviors shown in (a) and (b) are identical (color online)"

Fig. 14

Conventional oscillations without fast-slow characteristics in the system (5) for $ \beta<\frac{2\sqrt{3}}{9} $. (a) $ \beta=0.38 $; (b) $ \beta=0.3 $. The other parameters are the same as in Fig. 13(c)"