Applied Mathematics and Mechanics (English Edition) ›› 2025, Vol. 46 ›› Issue (8): 1417-1432.doi: https://doi.org/10.1007/s10483-025-3279-6
Shun WENG1, Liying WU1, Zuoqiang LI1, Lanbin ZHANG2, Huliang DAI3,†( )
)
Received:2025-03-05
Revised:2025-06-02
Published:2025-07-28
Contact:
Huliang DAI, E-mail: daihulianglx@hust.edu.cnSupported by:2010 MSC Number:
Shun WENG, Liying WU, Zuoqiang LI, Lanbin ZHANG, Huliang DAI. Optimizing wind energy harvester with machine learning. Applied Mathematics and Mechanics (English Edition), 2025, 46(8): 1417-1432.
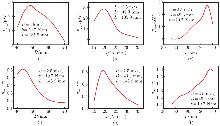
Fig. 5
Effects of D, k, and L on Pavg and ηaem at U=2.5 m/s: (a) D on Pavg with k=20.7 N/m and L=135.9 mm; (b) k on Pavg with D=49.3 mm and L=135.9 mm; (c) L on Pavg with D=49.3 mm and k=20.7 N/m; (d) D on ηaem with k=19.7 N/m and L=145.2 mm; (e) k on ηaem with D=43.3 mm and L=145.2 mm; (f) L on ηaem with D=49.3 mm and k=19.7 N/m (color online)"
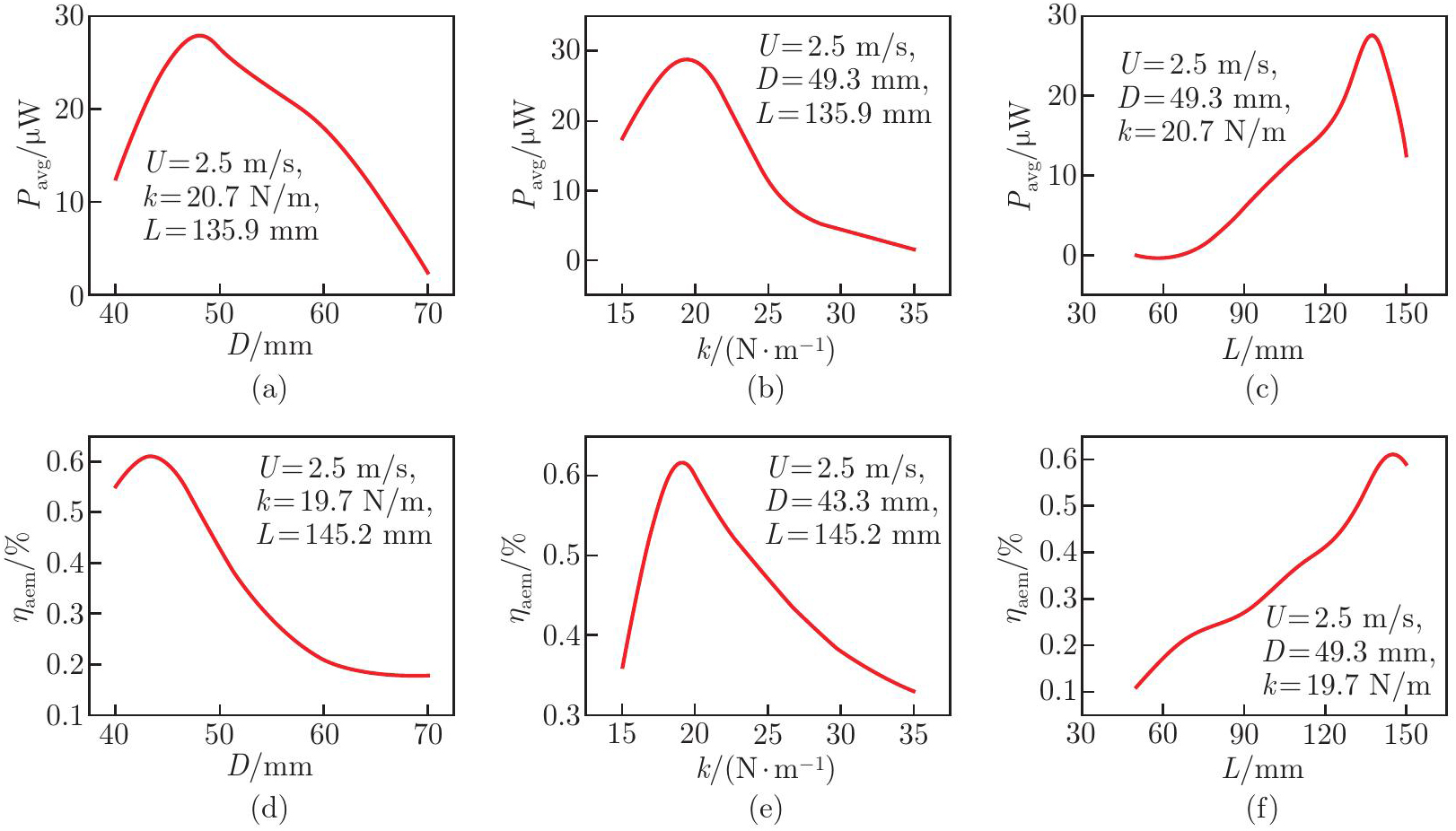
Fig. 6
Effects of D, k, and L on Pavg and ηaem at U=3.5 m/s: (a) D on Pavg with k=19.1 N/m and L=149.2 mm; (b) k on Pavg with D=40.2 mm and L=149.2 mm; (c) L on Pavg with D=40.2 mm and k=19.1 N/m; (d) D on ηaem with k=22.1 N/m and L=139.2 mm; (e) k on ηaem with D=45.2 mm and L=139.2 mm; (f) L on ηaem with D=45.2 mm and k=22.1 N/m (color online)"
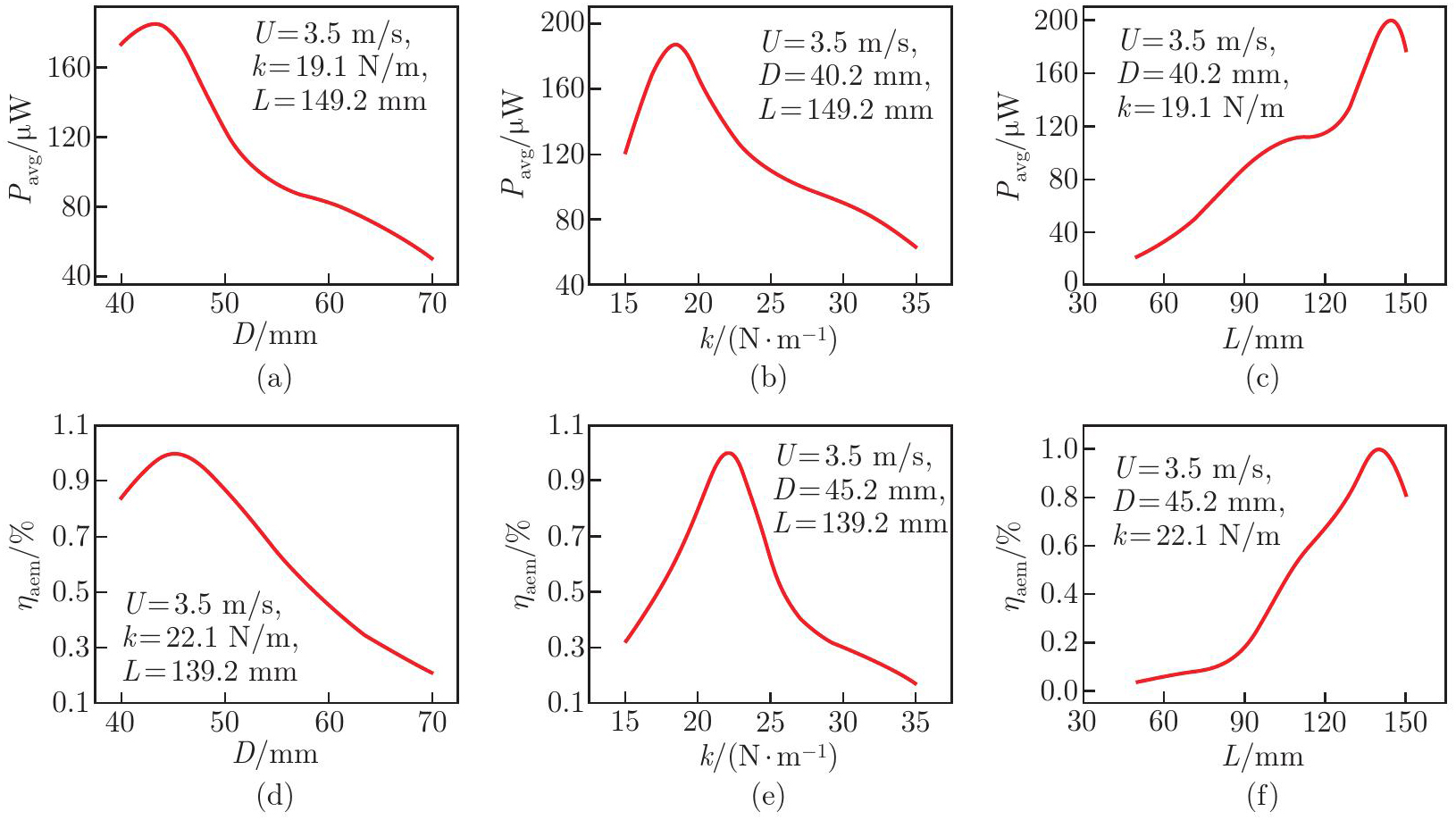
Fig. 7
Effects of D, k, and L on Pavg and ηaem at U=4.5 m/s: (a) D on Pavg with k=27.3 N/m and L=125.2 mm; (b) k on Pavg with D=58.2 mm and L=125.2 mm; (c) L on Pavg with D=58.2 mm and k=27.3 N/m; (d) D on ηaem with k=26.7 N/m and L=113.2 mm; (e) k on ηaem with D=63.7 mm and L=113.2 mm; (f) L on ηaem with D=63.7 mm and k=26.7 N/m (color online)"
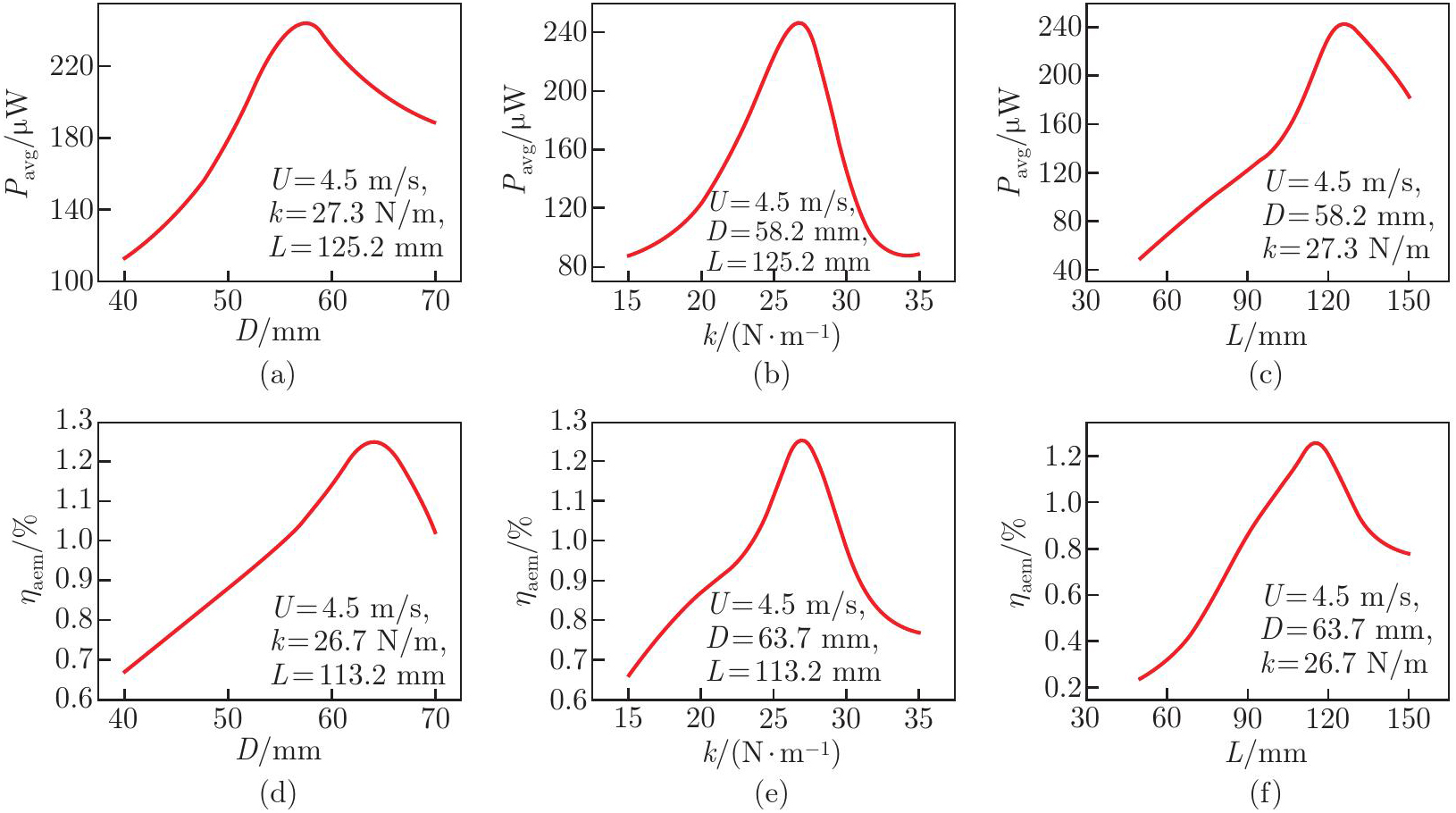
Fig. 8
Effects of D, k, and L on Pavg and ηaem) at U=5.5 m/s: (a) D on Pavg with k=27.4 N/m and L=115.5 mm; (b) k on Pavg with D=57.4 mm and L=115.5 mm; (c) L on Pavg with D=57.4 mm and k=27.4 N/m; (d) D on ηaem with k=31.8 N/m and L=131.1 mm; (e) k on ηaem with D=60.1 mm and L=131.1 mm; (f) L on ηaem with D=60.1 mm and k=31.8 N/m (color online)"
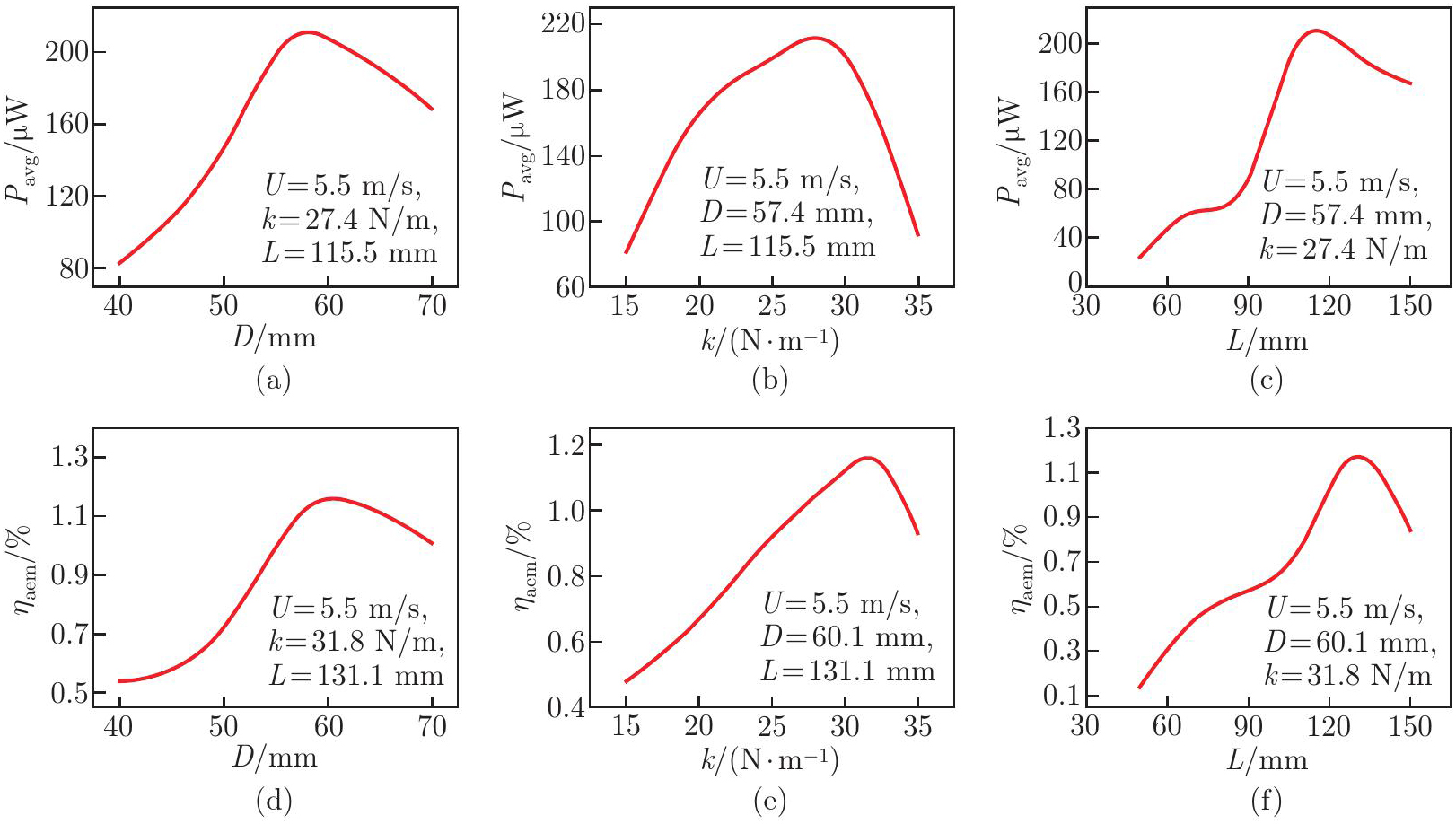
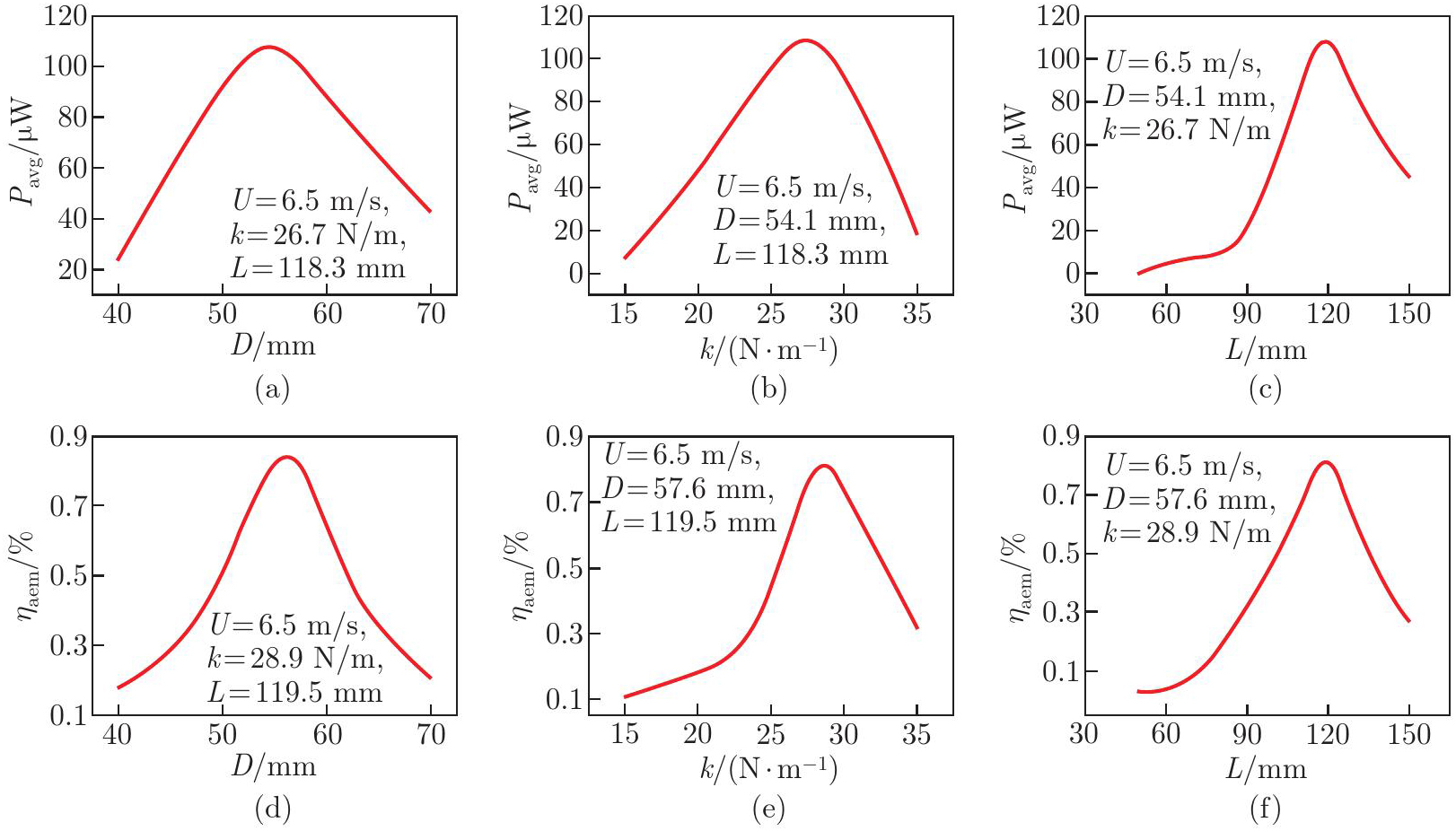
Fig. 9
Effects of D, k, and L on Pavg and ηaem at U=6.5 m/s: (a) D on Pavg with k=26.7 N/m and L=118.3 mm; (b) k on Pavg with D=54.1 mm and L=118.3 mm; (c) L on Pavg with D=54.1 mm and k=26.7 N/m; (d) D on ηaem with k=28.9 N/m and L=119.5 mm; (e) k on ηaem with D=57.6 mm and L=119.5 mm; (f) L on ηaem with D=57.6 mm and k=28.9 N/m (color online)"
| [1] | AL-SHETWI, A. Q. Sustainable development of renewable energy integrated power sector: trends, environmental impacts, and recent challenges. Science of The Total Environment, 822, 153645 (2022) |
| [2] | CAO, D. X., WANG, J. R., GUO, X. Y., LAI, S. K., and SHEN, Y. J. Recent advancement of flow-induced piezoelectric vibration energy harvesting techniques: principles, structures, and nonlinear designs. Applied Mathematics and Mechanics (English Edition), 43(7), 959–978 (2022) https://doi.org/10.1007/s10483-022-2867-7 |
| [3] | LIU, X. G., LI, Y. J., ZENG, L., LI, X., CHEN, N., BAI, S. B., HE, H. N., WANG, Q., and ZHANG, C. H. A review on mechanochemistry: approaching advanced energy materials with Greener force. Advanced Materials, 34(46), 2108327 (2022) |
| [4] | YU, N., FEI, X. Y., WU, C. Y., and YAN, B. Modeling and analysis of magnetic spring enhanced lever-type electromagnetic energy harvesters. Applied Mathematics and Mechanics (English Edition), 43(5), 743–760 (2022) https://doi.org/10.1007/s10483-022-2849-9 |
| [5] | GUO, X. G., ZHANG, Y. L., FAN, K. Q., LEE, C., and WANG, F. A comprehensive study of non-linear air damping and “pull-in” effects on the electrostatic energy harvesters. Energy Conversion and Management, 203, 112264 (2020) |
| [6] | ZHANG, L. B., HE, Y. X., MENG, B., DAI, H. L., and WANG, L. Unlocking multidirectional and broadband wind energy harvesting with triboelectric nanogenerator and vortex-induced vibration of sphere. Applied Mathematics and Mechanics (English Edition), 45(11), 1895–1912 (2024) https://doi.org/10.1007/s10483-024-3185-8 |
| [7] | WANG, Q., CHEN, Z. W., ZHAO, L. C., LI, M., ZOU, H. X., WEI, K. X., ZHANG, X. Z., and ZHANG, W. M. Enhanced galloping energy harvester with cooperative mode of vibration and collision. Applied Mathematics and Mechanics (English Edition), 43(7), 945–958 (2022) https://doi.org/10.1007/s10483-022-2869-9 |
| [8] | LU, K., HU, R. C., WANG, X. F., and DENG, Z. C. Multi-directional and ultra-low frequency energy harvester utilizing tunable buckled piezoelectric film. Mechanical Systems and Signal Processing, 210, 111137 (2024) |
| [9] | LAI, Z. H., WANG, S. B., ZHU, L. K., ZHANG, G. Q., WANG, J. L., YANG, K., and YURCHENKO, D. A hybrid piezo-dielectric wind energy harvester for high-performance vortex-induced vibration energy harvesting. Mechanical Systems and Signal Processing, 150, 107212 (2021) |
| [10] | LI, H. T., ZHENG, T. Y., QIN, W. Y., TIAN, R. L., DING, H., JI, J. C., and CHEN, L. Q. Theoretical and experimental study of a bi-stable piezoelectric energy harvester under hybrid galloping and band-limited random excitations. Applied Mathematics and Mechanics (English Edition), 45(3), 461–478 (2024) https://doi.org/10.1007/s10483-024-3098-5 |
| [11] | BOUMA, A., LE, E., VASCONCELLOS, R., and ABDELKE, A. Effective design and characterization of flutter-based piezoelectric energy harvesters with discontinuous nonlinearities. Energy, 238, 121662 (2022) |
| [12] | ZHOU, G. B., LI, Z. X., ZHU, Z. C., HAO, B. L., and TANG, C. Q. A new piezoelectric bimorph energy harvester based on the vortex-induced-vibration applied in rotational machinery. IEEE/ASME Transactions on Mechatronics, 24(2), 700–709 (2019) |
| [13] | ZHANG, M. J., ZHANG, C. Y., ABDELKEFI, A., YU, H. Y., GAIDAI, O., QIN, X., ZHU, H. J., and WANG, J. L. Piezoelectric energy harvesting from vortex-induced vibration of a circular cylinder: effect of Reynolds number. Ocean Engineering, 235, 109378 (2021) |
| [14] | MEHDIPOUR, I., MADARO, F., RIZZI, F., and DE VITTORIO, M. Comprehensive experimental study on bluff body shapes for vortex-induced vibration piezoelectric energy harvesting mechanisms. Energy Conversion and Management: X, 13, 100174 (2022) |
| [15] | HU, G., LIU, F. X., LI, L. X., LI, C., XIAO, Y. Q., and KWOK, K. C. S. Wind energy harvesting performance of tandem circular cylinders with triangular protrusions. Journal of Fluids and Structures, 91, 102780 (2019) |
| [16] | WANG, J. L., GU, S. H., ZHANG, C. Y., HU, G. B., CHEN, G., YANG, K., LI, H., LAI, Y. Y., LITAK, G., and YURCHENKO, D. Hybrid wind energy scavenging by coupling vortex-induced vibrations and galloping. Energy Conversion and Management, 213, 112835 (2020) |
| [17] | YANG, K., SU, K. W., WANG, J. L., WANG, J. F., YIN, K., and LITAK, G. Piezoelectric wind energy harvesting subjected to the conjunction of vortex-induced vibration and galloping: comprehensive parametric study and optimization. Smart Materials and Structures, 29(7), 075035 (2020) |
| [18] | LI, Z. Y., ZHANG, H. R., LITAK, G., and ZHOU, S. X. Periodic solutions and frequency lock-in of vortex-induced vibration energy harvesters with nonlinear stiffness. Journal of Sound and Vibration, 568, 117952 (2024) |
| [19] | WEI, N., ZHANG, Z. H., CHENG, G. M., YANG, H., HU, Y. L., and WEN, J. M. Study of a vortex-induced vibration piezoelectric wind energy harvester based on the synergy of multi-degree-of-freedom technology and magnetic nonlinear technology. Mechanical Systems and Signal Processing, 214, 111381 (2024) |
| [20] | SUN, W., JO, S., and SEOK, J. Development of the optimal bluff body for wind energy harvesting using the synergetic effect of coupled vortex induced vibration and galloping phenomena. International Journal of Mechanical Sciences, 156, 435–445 (2019) |
| [21] | HE, R. Y., SUN, H. Y., GAO, X. X., and YANG, H. X. Wind tunnel tests for wind turbines: a state-of-the-art review. Renewable and Sustainable Energy Reviews, 166, 112675 (2022) |
| [22] | ZHAO, Y., LI, R. B., FENG, L., WU, Y., NIU, J. L., and GAO, N. P. Boundary layer wind tunnel tests of outdoor airflow field around urban buildings: a review of methods and status. Renewable and Sustainable Energy Reviews, 167, 112717 (2022) |
| [23] | TOMINAGA, Y., WANG, L., ZHAI, Z. Q., and STATHOPOULOS, T. Accuracy of CFD simulations in urban aerodynamics and microclimate: progress and challenges. Building and Environment, 243, 110723 (2023) |
| [24] | HU, G. and KWOK, K. C. S. Predicting wind pressures around circular cylinders using machine learning techniques. Journal of Wind Engineering and Industrial Aerodynamics, 198, 104099 (2020) |
| [25] | PANCHIGAR, D., KAR, K., SHUKLA, S., MATHEW, R. M., CHADHA, U., and SELVARAJ, S. K. Machine learning-based CFD simulations: a review, models, open threats, and future tactics. Neural Computing and Applications, 34(24), 21677–21700 (2022) |
| [26] | ZHAO, Y. M., AKOLEKAR, H. D., WEATHERITT, J., MICHELASSI, V., and SANDBERG, R. D. RANS turbulence model development using CFD-driven machine learning. Journal of Computational Physics, 411, 109413 (2020) |
| [27] | SONG, T., DING, L., YANG, L., RAN, J. Y., and ZHANG, L. Comparison of machine learning models for performance evaluation of wind-induced vibration piezoelectric energy harvester with fin-shaped attachments. Ocean Engineering, 280, 114630 (2023) |
| [28] | ZHANG, C. Y., HU, G., YURCHENKO, D., LIN, P. F., GU, S. H., SONG, D. R., PENG, H. Y., and WANG, J. L. Machine learning based prediction of piezoelectric energy harvesting from wake galloping. Mechanical Systems and Signal Processing, 160, 107876 (2021) |
| [29] | ZHANG, Y. X., DUAN, J. Q., JIN, Y. F., and LI, Y. Discovering governing equation from data for multi-stable energy harvester under white noise. Nonlinear Dynamics, 106(4), 2829–2840 (2021) |
| [30] | LI, K., KOU, J. Q., and ZHANG, W. W. Unsteady aerodynamic reduced-order modeling based on machine learning across multiple airfoils. Aerospace Science and Technology, 119, 107173 (2021) |
| [31] | LI, W. J., ZHANG, D. H., and SHI, X. F. Establishment of a flow-induced vibration power database based on deep neural network machine learning method. Ocean Engineering, 285, 115463 (2023) |
| [32] | LIAO, Y. B., QIAN, F., ZHANG, R. Y., and KUMAR, P. Long short-term memory (LSTM) neural networks for predicting dynamic responses and application in piezoelectric energy harvesting. Smart Materials and Structures, 33(7), 075005 (2024) |
| [33] | CAI, W. and HARNE, R. L. A machine learning approach for maximizing direct current power of nonlinear energy harvesting systems subjected to periodic impulse excitation. Mechanical Systems and Signal Processing, 164, 108262 (2022) |
| [34] | WU, W. H., SUN, H., LV, B. C., and BERNITSAS, M. M. Modelling of a hydrokinetic energy converter for flow-induced vibration based on experimental data. Ocean Engineering, 155, 392–410 (2018) |
| [35] | WANG, W. Y., YIN, N., WU, Z. S., and ZHANG, Z. N. Omnidirectional energy harvesting with 3D-TENG for vibration diagnosis. Chemical Engineering Journal, 509, 161022 (2025) |
| [36] | FACCHINETTI, M. L., DE LANGRE, E., and BIOLLEY, F. Coupling of structure and wake oscillators in vortex-induced vibrations. Journal of Fluids and Structures, 19(2), 123–140 (2004) |
| [37] | YU, Q. X., HOU, Z. S., BU, X. H., and YU, Q. F. RBFNN-based data-driven predictive iterative learning control for nonaffine nonlinear systems. IEEE Transactions on Neural Networks and Learning Systems, 31(4), 1170–1182 (2020) |
| [38] | PANDA, S. and PANDA, G. On the development and performance evaluation of improved radial basis function neural networks. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 52(6), 3873–3884 (2022) |
| [39] | LIU, Z. Q., WANG, Y. Z., and HUA, X. G. Numerical studies and proposal of design equations on cylindrical oscillating wave surge converters under regular waves using SPH. Energy Conversion and Management, 203, 112242 (2020) |
| [40] | WENG, S., WU, L. Y., ZHANG, L. B., GAO, K., ZHANG, J. S., ZHANG, Z. Y., and DAI, H. L. Multi-directional wind energy harvesting based on the coupling effect between a piezoelectric beam and an elastic-supported sphere. Journal of Zhejiang University-SCIENCE A, 26, 512–524 (2025) |
| [1] | Tianchang DENG, Hu DING, S. KITIPORNCHAI, Jie YANG. Machine learning-based design strategy for weak vibration pipes conveying fluid [J]. Applied Mathematics and Mechanics (English Edition), 2025, 46(7): 1215-1236. |
| [2] | Lanbin ZHANG, Yixiang HE, Bo MENG, Huliang DAI, Lin WANG. Unlocking multidirectional and broadband wind energy harvesting with triboelectric nanogenerator and vortex-induced vibration of sphere [J]. Applied Mathematics and Mechanics (English Edition), 2024, 45(11): 1895-1912. |
| [3] | Jiajie GONG, Xinyue LIU, Yancong ZHANG, Fengping ZHU, Guohui HU. Prediction of single cell mechanical properties in microchannels based on deep learning [J]. Applied Mathematics and Mechanics (English Edition), 2024, 45(11): 1857-1874. |
| [4] | Xiang MU, Xiaoyu FU, Liangliang ZHANG, Zhaowei ZHU, Jinming ZHANG, Yang GAO. Fundamental solutions of critical wedge angles for one-dimensional piezoelectric quasicrystal wedge [J]. Applied Mathematics and Mechanics (English Edition), 2022, 43(5): 709-728. |
| [5] | Chuansai ZHOU, Haochen LI, Chen YU, Jiangjiang XIA, Pingwen ZHANG. A station-data-based model residual machine learning method for fine-grained meteorological grid prediction [J]. Applied Mathematics and Mechanics (English Edition), 2022, 43(2): 155-166. |
| [6] | Lianhe LI, Xiaowei CUI, Junhong GUO. Interaction between a screw dislocation and an elliptical hole with two asymmetrical cracks in a one-dimensional hexagonal quasicrystal with piezoelectric effect [J]. Applied Mathematics and Mechanics (English Edition), 2020, 41(6): 899-908. |
| [7] | Lianhe LI, Guanting LIU. Study on a straight dislocation in an icosahedral quasicrystal with piezoelectric effects [J]. Applied Mathematics and Mechanics (English Edition), 2018, 39(9): 1259-1266. |
| [8] | FU Yi-ming;RUAN Jian-li. Nonlinear active control of damaged piezoelectric smart laminated plates and damage detection [J]. Applied Mathematics and Mechanics (English Edition), 2008, 29(4): 421-436 . |
| [9] | SHEN Hui-shen. THERMO-PIEZOELECTRIC EFFECTS ON THE POSTBUCKLING OF AXIALLY-LOADED HYBRID LAMINATED CYLINDRICAL PANELS [J]. Applied Mathematics and Mechanics (English Edition), 2004, 25(1): 24-38. |
| Viewed | ||||||
|
Full text |
|
|||||
|
Abstract |
|
|||||


 Email Alert
Email Alert RSS
RSS