Applied Mathematics and Mechanics (English Edition) ›› 2025, Vol. 46 ›› Issue (1): 139-156.doi: https://doi.org/10.1007/s10483-025-3203-6
Previous Articles Next Articles
H. HOSSEINI†( ), O. BALILASHAKI
), O. BALILASHAKI
Received:2024-08-14
Revised:2024-10-30
Online:2025-01-03
Published:2025-01-06
Contact:
H. HOSSEINI
E-mail:h.hoseini@gu.ac.ir
2010 MSC Number:
H. HOSSEINI, O. BALILASHAKI. Dynamic stress concentration in an infinitely long cylindrical cavity due to a point spherical source embedded within a fluid-saturated poroelastic formation of infinite extent. Applied Mathematics and Mechanics (English Edition), 2025, 46(1): 139-156.
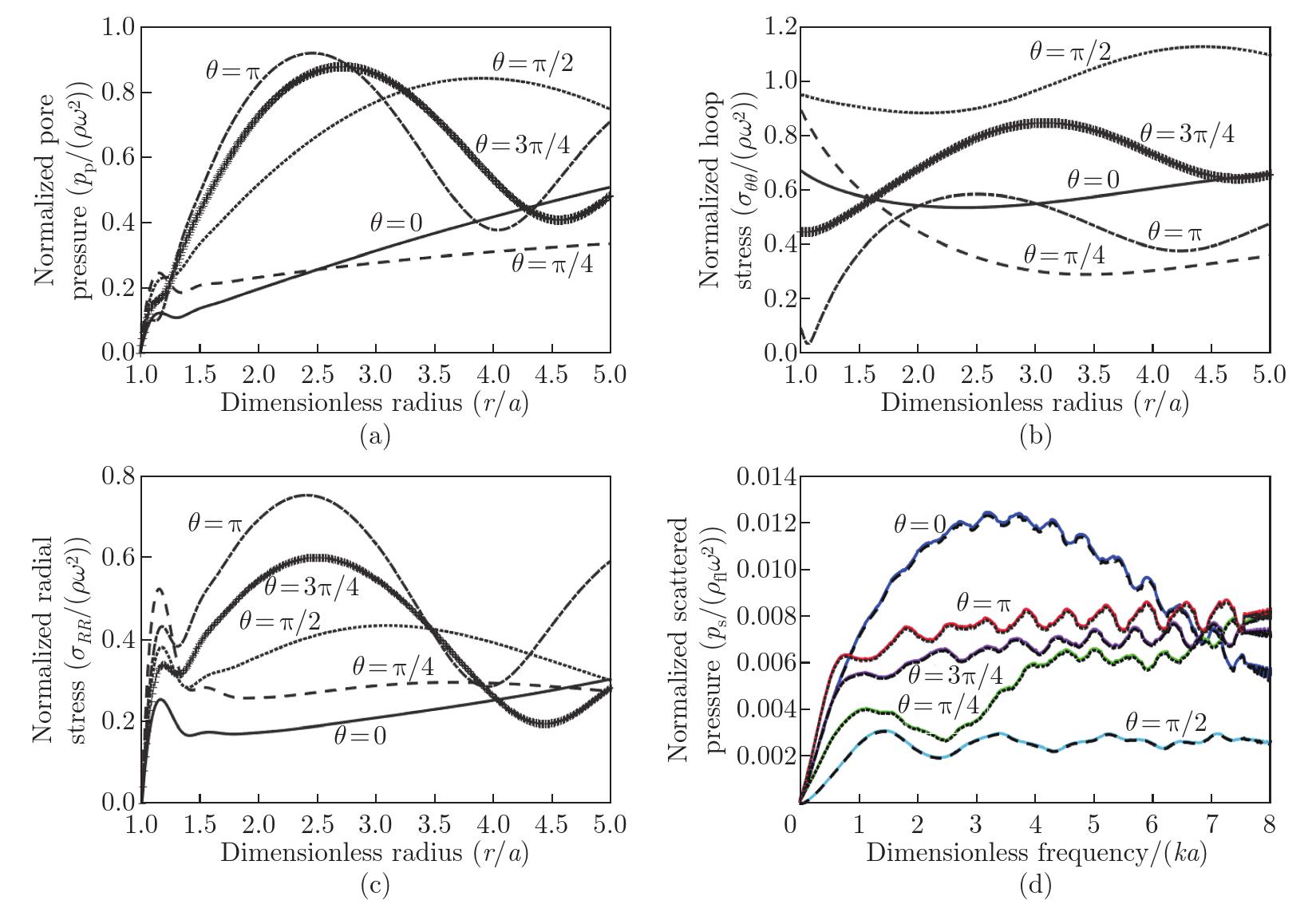
Fig. 8
(a) Normalized pore pressure, (b) normalized hoop stress, and (c) normalized radial stress versus the dimensionless radius (checked by Refs. [9] and [18]). (d) Normalized scattered pressure versus the dimensionless frequency (rigid cylinder case, checked by Ref. [41]). Dashed curves are for the present results, while solid curves are from the references (color online)"
| [1] | GASSMANN, F. Über die elastizität poröser medien. Vierteljahrsschrift der Naturforschenden Gesellschaft in Zurich, 96, 1–23 (1951) |
| [2] | BIOT, M. A. Theory of propagation of elastic waves in a fluid-saturated porous solid, I: low-frequency range. The Journal of the Acoustical Society of America, 28, 168–178 (1956) |
| [3] | BIOT, M. A. Theory of propagation of elastic waves in a fluid-saturated porous solid, II: higher frequency range. The Journal of the Acoustical Society of America, 28, 179–191 (1956) |
| [4] | BIOT, M. A. Mechanics of deformation and acoustic propagation in porous media. Journal of Applied Physics, 33, 1482–1498 (1962) |
| [5] | PLONA, T. J. Observation of a second bulk compressional wave in a porous medium at ultrasonic frequencies. Applied Physics Letters, 36, 259–261 (1980) |
| [6] | MOW, C. C. and MENTE, L. J. Dynamic stresses and displacements around cylindrical discontinuities due to plane harmonic shear waves. Journal of Applied Mechanics, 30, 598–604 (1963) |
| [7] | MOW, C. C. and PAO, Y. H. The Diffraction of Elastic Waves and Dynamic Stress Concentrations, The Rand Corporation, Santa Monica (1971) |
| [8] | BERRYMAN, J. G. Scattering by a spherical inhomogeneity in a fluid-saturated porous medium. Journal of Mathematical Physics, 26, 1408–1419 (1985) |
| [9] | MEI, C. C., SI, B. I., and CAI, D. Scattering of simple harmonic waves by a circular cavity in a fluid-infiltrated poroelastic medium. Wave Motion, 6, 265–278 (1984) |
| [10] | GALVIN, R. J. and GUREVICH, B. Scattering of a longitudinal wave by a circular crack in a fluid-saturated porous medium. International Journal of Solids and Structures, 44, 7389–7398 (2007) |
| [11] | YUAN, X. and LIAO, Z. P. Scattering of plane SH waves by a cylindrical alluvial valley of circular-arc cross-section. Earthquake Engineering and Structural Dynamics, 24, 1303–1313 (1995) |
| [12] | CAO, H. and LEE, V. W. Scattering and diffraction of plane P waves by circular-cylindrical canyons with variable depth-to-width ratio. Soil Dynamics and Earthquake Engineering, 9, 141–150 (1990) |
| [13] | SENJUNTICHAI, T. and RAJAPAKSE, R. K. N. D. Transient response of a circular cavity in a poroelastic medium. International Journal for Numerical and Analytical Methods in Geomechanics, 17, 357–383 (1993) |
| [14] | GUREVICH, B., SADOVNICHAJA, A. P., LOPATNIKOV, S. L., and SHAPIRO, S. A. Scattering of a compressional wave in a poroelastic medium by an ellipsoidal inclusion. Geophysical Journal International, 133, 91–103 (1998) |
| [15] | ZHOU, X. L., WANG, J. H., XU, B., and JIANG, L. F. Dynamic response of a circular pipeline in a poroelastic medium. Mechanics Research Communications, 36, 898–905 (2009) |
| [16] | MOORE, I. D. and GUAN, F. Three-dimensional dynamic response of lined tunnels due to incident seismic waves. Earthquake Engineering and Structural Dynamics, 25, 357–369 (1996) |
| [17] | KATTIS, S. E., BESKOS, D. E., and CHENG, A. H. D. 2D dynamic response of unlined and lined tunnels in poroelastic soil to harmonic body waves. Earthquake Engineering and Structural Dynamics, 32, 97–110 (2003) |
| [18] | GATMIRI, B. and ESLAMI, H. Wave scattering in cross-anisotropic porous media around the cavities and inclusions. Soil Dynamics and Earthquake Engineering, 28, 1014–1027 (2008) |
| [19] | YI, C., ZHANG, P., JOHANSSON, D., and NYBERG, U. Dynamic response of a circular lined tunnel with an imperfect interface subjected to cylindrical P-waves. Computers and Geotechnics, 55, 165–171 (2014) |
| [20] | YI, C., LU, W. B., ZHANG, P., JOHANSSON, D., and NYBERG, U. Effect of imperfect interface on the dynamic response of a circular lined tunnel impacted by plane P-waves. Tunneling and Underground Space Technology, 51, 68–74 (2016) |
| [21] | TAO, M., ZHAO, H. T., LI, Z. W., and ZHU, J. B. Analytical and numerical study of a circular cavity subjected to plane and cylindrical P-wave scattering. Tunnelling and Underground Space Technology, 95, 103143 (2020) |
| [22] | FAN, Z., ZHANG, J., and XU, H. Theoretical study of the dynamic response of a circular lined tunnel with an imperfect interface subjected to incident SV-waves. Computers and Geotechnics, 110, 308–318 (2019) |
| [23] | TAN, Y., YANG, M., and LI, X. Dynamic response of a circular lined tunnel with an imperfect interface embedded in the unsaturated poroelastic medium under P wave. Computer and Geotechnics, 122, 103514 (2020) |
| [24] | HASHEMINEJAD, S. M. and HOSSEINI, H., Radiation loading of a cylindrical source in a fluid-filled cylindrical cavity embedded within a fluid-saturated poroelastic medium. The Journal of Applied Mechanics, 69, 675–683 (2002) |
| [25] | HASHEMINEJAD, S. M. and HOSSEINI, H. Nonaxisymmetric interaction of a spherical radiator in a fluid-filled permeable borehole. International Journal of Solids and Structures, 45, 24–47 (2008) |
| [26] | HASHEMINEJAD, S. M. and HOSSEINI, H. Dynamic interaction of a spherical radiator in a fluid-filled cylindrical borehole within a poroelastic formation. Mechanics Research Communications, 35, 158–171 (2008) |
| [27] | KUBENKO, V. D. and DZYUBA, V. V. The acoustic field in a rigid cylindrical vessel excited by a sphere oscillating by a definite law. International Applied Mechanics, 36, 779–788 (2000) |
| [28] | YUAN, Z., CAI, Y., and CAO, Z. An analytical model for vibration prediction of a tunnel embedded in a saturated full-space to a harmonic point load. Soil Dynamics and Earthquake Engineering, 86, 25–40 (2016) |
| [29] | LU, S., ZHOU, C., ZHANG, Z., and JIANG. N., Dynamic stress concentration of surrounding rock of a circular tunnel subjected to blasting cylindrical P-waves. Geotechnical and Geological Engineering, 37, 2363–2371 (2019) |
| [30] | YUAN, Z., BOSTRÖM, A., CAI, Y., and CAO, Z. Analytical wave function method for modelling a twin tunnel embedded in a saturated poroelastic full-space. Computers and Geotechnics, 114, 103114 (2019) |
| [31] | LI, T. and UEDA, M. Sound scattering of a plane wave obliquely incident on a cylinder. The Journal of the Acoustical Society of America, 86, 2363–2368 (1989) |
| [32] | MAZE, G., LEON, F., and VEKSLER, N. D. Scattering of an obliquely incident plane acoustic wave by a circular cylindrical shell: experimental results. Acta Acustica United with Acustica, 84, 1–11 (1998) |
| [33] | HONARVAR, F. and SINCLAIR, A. N. Scattering of an obliquely incident plane wave from a circular clad rod. The Journal of the Acoustical Society of America, 102, 41–48 (1997) |
| [34] | FLAX, L., VARADAN, V. K., and VARADAN, V. V. Scattering of an obliquely incident acoustic wave by an infinite cylinder. The Journal of the Acoustical Society of America, 68, 1832–1835 (1980) |
| [35] | MITRI, F. G. Acoustic backscattering enhancements resulting from the interaction of an obliquely incident plane wave with an infinite cylinder. Ultrasonics, 50, 675–682 (2010) |
| [36] | LAPERRE, J. and THYS, W. Scattering of ultrasonic waves by an immersed porous cylinder. Acoustic Letter, 16, 9–16 (1992) |
| [37] | ZHU, C., LIU, L., SONG, Z., LIU, Y., and LIU, Q. H. An efficient exact numerical solution for scattering by a circular cylinder. IEEJ Transactions on Electrical and Electronic Engineering, 11, S3–S10 (2016) |
| [38] | MUHLESTEIN, M. B., GOLDSBERRY, B. M., NORRIS, A. N., and HABERMAN, M. R. Acoustic scattering from a fluid cylinder with Willis constitutive properties. The Royal Society Publishing, 474, 20180571 (2018) |
| [39] | CHEN, S., ZHAO, W., and WAN, D. On the scattering of focused wave by a finite surface-piercing circular cylinder: a numerical investigation. Physics of Fluids, 34, 035132 (2022) |
| [40] | OU, M. J. Y. and LEMOINE, G. I. Time-harmonic analytic solution for an acoustic plane wave scattering of an isotropic poroelastic cylinder: convergence and form function. Journal of Computational Acoustics, 24, 1550017 (2016) |
| [41] | LI, T. and UEDA, M. Sound scattering of a spherical wave incident on a cylinder. The Journal of the Acoustical Society of America, 87, 1871–1879 (1990) |
| [42] | PIQUETTE, J. C. Spherical wave scattering by an elastic solid cylinder of infinite length. The Journal of the Acoustical Society of America, 79, 1248–1259 (1986) |
| [43] | HOSSEINI, H. and NAMAZI, N. Acoustic scattering of spherical waves incident on a long fluid-saturated poroelastic cylinder. Acta Mechanica, 223, 2075–2089 (2012) |
| [44] | BOURBIE, T., COUSSY, O., and ZINSZNER, B. Acoustics of Porous Media, Gulf Publishing Company, Houston (1987) |
| [45] | IVANOV, Y. A. Diffraction of Electromagnetic Waves on Two Bodies, National Aeronautics and Space Administration, Washington, D. C. (1970) |
| [46] | JOHNSON, D. L., PLONA, T. J., and KOJIMA, H. Probing porous media with first and second sound, II: acoustic properties of water saturated porous media. Journal of Applied Physics, 76, 115–125 (1994) |
| [47] | LO, W. C., SPOSITO, G., and MAJER, E. Low-frequency dilatational wave propagation through fully-saturated poroelastic media. Advances in Water Resources, 29, 408–416 (2006) |
| [48] | CARCIONE, J. M., CAVALLINI, F., SANTOS, J. E., RAVAZZOLI, C. L., and GAUZELLINO, P. M. Wave propagation in partially saturated porous media: simulation of a second slow wave. Wave Motion, 39, 227–240 (2004) |
| [49] | ABRAMOVITZ, M. and STEGUN, I. Handbook of Mathematical Functions, National Bureau of Standards, Washington, D. C. (1964) |
| [1] | N. HUMNEKAR, D. SRINIVASACHARYA. Influence of variable viscosity and double diffusion on the convective stability of a nanofluid flow in an inclined porous channel [J]. Applied Mathematics and Mechanics (English Edition), 2024, 45(3): 563-580. |
| [2] | L.I. KUZMINA, Y.V. OSIPOV, A.R. PESTEREV. Deep bed filtration model for cake filtration and erosion [J]. Applied Mathematics and Mechanics (English Edition), 2024, 45(2): 355-372. |
| [3] | L. ANITHA, B. J. GIREESHA. Convective flow of Jeffrey nanofluid along an upright microchannel with Hall current and Buongiorno model: an irreversibility analysis [J]. Applied Mathematics and Mechanics (English Edition), 2023, 44(9): 1613-1628. |
| [4] | K. RAMESH, M. G. REDDY, B. SOUAYEH. Electro-magneto-hydrodynamic flow of couple stress nanofluids in micro-peristaltic channel with slip and convective conditions [J]. Applied Mathematics and Mechanics (English Edition), 2021, 42(4): 593-606. |
| [5] | T. HAYAT, K. MUHAMMAD, A. ALSAEDI. Melting effect and Cattaneo-Christov heat flux in fourth-grade material flow through a Darcy-Forchheimer porous medium [J]. Applied Mathematics and Mechanics (English Edition), 2021, 42(12): 1787-1798. |
| [6] | L. I. KUZMINA, Y. V. OSIPOV, T. N. GORBUNOVA. Asymptotics for filtration of polydisperse suspension with small impurities [J]. Applied Mathematics and Mechanics (English Edition), 2021, 42(1): 109-126. |
| [7] | P. K. YADAV, A. TIWARI, P. SINGH. Motion through spherical droplet with non-homogenous porous layer in spherical container [J]. Applied Mathematics and Mechanics (English Edition), 2020, 41(7): 1069-1082. |
| [8] | T. SAEED, I. A. ABBAS. Analysis of thermal responses in a two-dimensional porous medium caused by pulse heat flux [J]. Applied Mathematics and Mechanics (English Edition), 2020, 41(6): 927-938. |
| [9] | S. A. SHEHZAD, S. U. KHAN, Z. ABBAS, A. RAUF. A revised Cattaneo-Christov micropolar viscoelastic nanofluid model with combined porosity and magnetic effects [J]. Applied Mathematics and Mechanics (English Edition), 2020, 41(3): 521-532. |
| [10] | H. WAQAS, M. IMRAN, S. U. KHAN, S. A. SHEHZAD, M. A. MERAJ. Slip flow of Maxwell viscoelasticity-based micropolar nanoparticles with porous medium: a numerical study [J]. Applied Mathematics and Mechanics (English Edition), 2019, 40(9): 1255-1268. |
| [11] | Qingxiang LI, Ming PAN, Quan ZHOU, Yuhong DONG. Drag reduction of turbulent channel flows over an anisotropic porous wall with reduced spanwise permeability [J]. Applied Mathematics and Mechanics (English Edition), 2019, 40(7): 1041-1052. |
| [12] | A. RAUF, Z. ABBAS, S. A. SHEHZAD. Utilization of Maxwell-Cattaneo law for MHD swirling flow through oscillatory disk subject to porous medium [J]. Applied Mathematics and Mechanics (English Edition), 2019, 40(6): 837-850. |
| [13] | M. SHEIKHOLESLAMI. Investigation of Coulomb force effects on ethylene glycol based nanofluid laminar flow in a porous enclosure [J]. Applied Mathematics and Mechanics (English Edition), 2018, 39(9): 1341-1352. |
| [14] | P. K. YADAV, S. JAISWAL, B. D. SHARMA. Mathematical model of micropolar fluid in two-phase immiscible fluid flow through porous channel [J]. Applied Mathematics and Mechanics (English Edition), 2018, 39(7): 993-1006. |
| [15] | K. R. RAGHUNATHA, I. S. SHIVAKUMARA, SOWBHAGYA. Stability of buoyancy-driven convection in an Oldroyd-B fluid-saturated anisotropic porous layer [J]. Applied Mathematics and Mechanics (English Edition), 2018, 39(5): 653-666. |
| Viewed | ||||||
|
Full text |
|
|||||
|
Abstract |
|
|||||


 Email Alert
Email Alert RSS
RSS