Applied Mathematics and Mechanics (English Edition) ›› 2025, Vol. 46 ›› Issue (6): 1089-1106.doi: https://doi.org/10.1007/s10483-025-3255-6
Previous Articles Next Articles
Lixia MA1,2,3, Qiang ZHOU4, Lijun YI1,2,†( ), Ji WANG1
), Ji WANG1
Received:2024-11-07
Revised:2025-03-27
Published:2025-06-06
Contact:
Lijun YI, E-mail: yilijun@nbu.edu.cnSupported by:2010 MSC Number:
Lixia MA, Qiang ZHOU, Lijun YI, Ji WANG. A semi-analytical model and mechanism analysis for force-frequency effect and coefficient of square quartz. Applied Mathematics and Mechanics (English Edition), 2025, 46(6): 1089-1106.
Table 2
Values of R′1 and R′3 for square quartz under eccentrically concentrated loads based on Mathieu's exact solution and central stress results from anisotropic FEM simulations"
| Parallel to | Perpendicular to | |||
|---|---|---|---|---|
| 0 | -1.527 | 0.787 | 0.719 | -1.636 |
| 1 | -1.436 | 0.606 | 0.542 | -1.525 |
| 2 | -1.129 | 0.113 | 0.079 | -1.147 |
| 3 | -0.612 | -0.547 | -0.493 | -0.516 |
| 4 | -0.041 | -1.249 | -1.074 | 0.208 |
Table 4
Comparison among FFC results from our semi-analytical model (see Eq. (8) and Table 1 for concentrated loads), our modified anisotropic semi-analytical model (see Eq. (8) and Table 2 for concentrated loads, and Eq. (11) for distributed load), our nonlinear FEM solution, and published experimental results"
| Load type | FFC/(Hz·N-1) | Semi-analytical model/(Hz·N-1) | Modified anisotropic semi-analytical model/(Hz·N-1) | Nonlinear FEM simulation/(Hz·N-1) | ||||
|---|---|---|---|---|---|---|---|---|
| Perpendicular, eccentrically concentrated load | 0.46 | 3.58 | 8 | -11.11[ | ||||
| -8.89[ | ||||||||
| 1.11[ | 1.07 | |||||||
| 11.11[ | 10.98 | 13.32 | 12.59 | |||||
| Perpendicular, symmetrically concentrated load | 0.43 | 3.58 | 8 | -12[ | ||||
| Parallel, distributed load | 0.020 | 75 | 1 | 101 010* [ | 92 542.50 | 92 539.12 | 101 729.03 | |
| 0.041 7 | 37.88 | 2 | 7 952.1* [ | 11 804.06 | 11 803.01 | 10 674.91 | ||
| 0.1 | 16.11 | 3 | 1 819.6* [ | 970.93 | 970.96 | 1 110.62 | ||
| 0.1 | 16.11 | 3 | 804* [ | 970.93 | 970.96 | 1110.62 | ||
| 0.1 | 16.11 | 3 | 962.57* [ | 970.93 | 970.96 | 1110.62 | ||
| 0.1 | 16.11 | 3 | 595.96* [ | 970.93 | 970.96 | 1110.62 | ||
| * denotes the results obtained through load transfer efficiency. | ||||||||

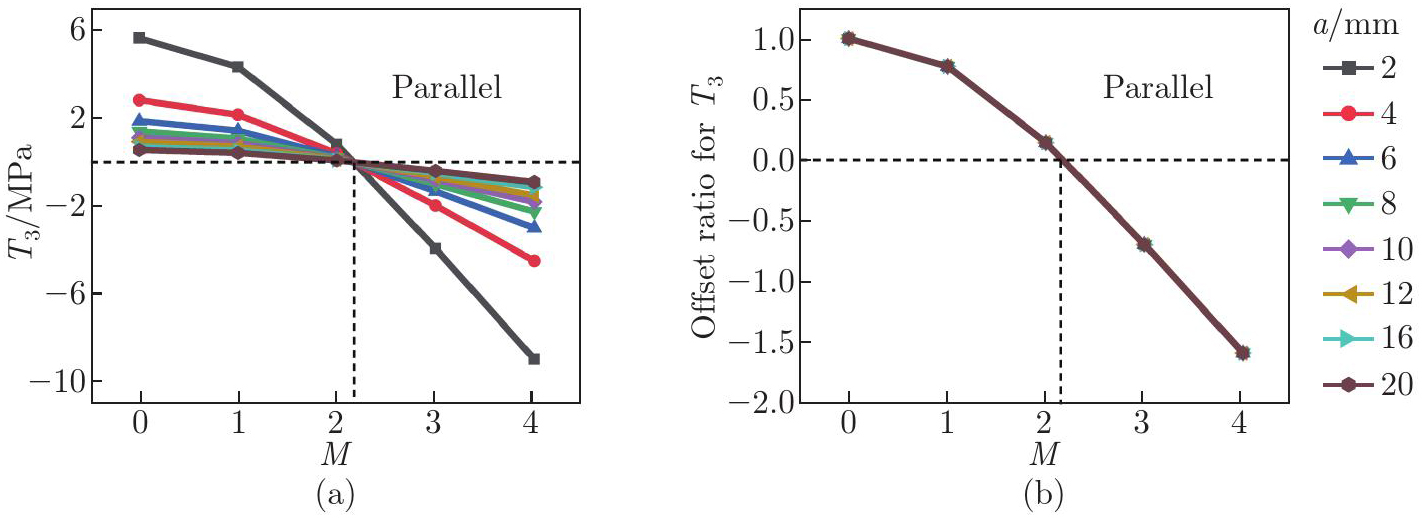
Fig. 8
Square QCRs with different side lengths under 1 N eccentrically concentrated load applied parallelly to the x1-axis based on FEM results: (a) initial stress component perpendicular to the x1-axis T3 and (b) offset ratio of T3 (the ratio of T3 at different M to T3 at M=0) with respect to the eccentricity (color online)"
| [1] | KIM, J., CAMPBELL, A. S., DE ÁVILA, B. E. F., and WANG, J. Wearable biosensors for healthcare monitoring. Nature Biotechnology, 37, 389–406 (2019) |
| [2] | OLSSON, T., HAAGE, M., KIHLMAN, H., JOHANSSON, R., NILSSON, K., ROBERTSSON, A., BJÖRKMAN, M., ISAKSSON, R., OSSBAHR, G., and BROGÅRDH, T. Cost-efficient drilling using industrial robots with high-bandwidth force feedback. Robotics and Computer-Integrated Manufacturing, 26, 24–38 (2010) |
| [3] | LOU, Y. J., WEI, J. H., and SONG, S. Design and optimization of a joint torque sensor for robot collision detection. IEEE Sensors Journal, 19, 6618–6627 (2019) |
| [4] | HAN, X., HUANG, M., WU, Z., GAO, Y., XIA, Y., YANG, P., FAN, S., LU, X., YANG, X., LIANG, L., L., SU, W., WANG, L., CUI, Z., ZHAO, Y., LI, Z., ZHAO, L., and JIANG, Z. Advances in high-performance MEMS pressure sensors: design, fabrication, and packaging. Microsystems & Nanoengineering, 9, 156 (2023) |
| [5] | XIE, J. and HU, Y. Electric admittance analysis of quartz crystal resonator in thickness-shear mode induced by array of surface viscoelastic micro-beams. Applied Mathematics and Mechanics (English Edition), 38(1), 29–38 (2017) https://doi.org/10.1007/s10483-017-2154-6 |
| [6] | LIU, Q., WANG, S., YAN, G., DING, H., WANG, H., SHI, Q., DING, X., and YU, H. A human-sensitive frequency band vibration isolator for heavy-duty truck seats. Applied Mathematics and Mechanics (English Edition), 45(10), 1733–1748 (2024) https://doi.org/10.1007/s10483-024-3177-8 |
| [7] | KONG, J., DING, B., WANG, W., WANG, Z., XIAO, J., and QIU, H. An electromagnetic semi-active dynamic vibration absorber for thin-walled workpiece vibration suppression in mirror milling. Applied Mathematics and Mechanics (English Edition), 45(8), 1315–1334 (2024) https://doi.org/10.1007/s10483-024-3132-7 |
| [8] | LAN, B. Y., TIAN, W. J., ZHAO, Q. J., and LV, Y. S. Study on the design and the stability of integrated quartz resonator. Advanced Materials Research, 846-847, 569–573 (2013) |
| [9] | EERNISSE, E. P., WARD, R. W., and WIGGINS, R. B. Survey of quartz bulk resonator sensor technologies. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 35, 323–330 (1988) |
| [10] | CHEN, J., YONG, Y. K., KUBENA, R., KIRBY, D., and CHANG, D. On the acceleration sensitivity and its active reduction by edge electrodes in AT-cut quartz resonators. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 62, 1104–1113 (2015) |
| [11] | CHEN, J. F. Nonlinear Acceleration Sensitivity and Frequency Temperature Behavior of Quartz Crystals, Ph. D. dissertation, Rutgers University (2016) |
| [12] | EERNISSE, E. P. and WIGGINS, R. B. Review of thickness-shear mode quartz resonator sensors for temperature and pressure. IEEE Sensors Journal, 1, 79–87 (2001) |
| [13] | KIRIKERA, G. R., PATTON, W., and BEHR, M. S. Modeling thickness shear mode quartz sensors for increased downhole pressure & temperature applications. Proceedings of the COMSOL Conference, COMSOL, Boston (2010) |
| [14] | HU, Y. T., CUI, Z. J., JIANG, S. N., and YANG, J. S. Thickness-shear vibration of circular crystal plate in cylindrical shell as pressure sensor. Applied Mathematics and Mechanics (English Edition), 27(6), 749–755 (2006) https://doi.org/10.1007/s10483-006-0605-z |
| [15] | CHEN, F., TIAN, W., and WEI, Y. Highly sensitive resonant sensor using quartz resonator cluster for inclination measurement. Review of Scientific Instruments, 91, 055005 (2020) |
| [16] | MUROZAKI, Y., NOGAWA, K., and ARAI, F. Miniaturized load sensor using quartz crystal resonator constructed through microfabrication and bonding. ROBOMECH Journal, 1, 3 (2014) |
| [17] | FU, H., CHEN, C., WANG, C., CHAO, M., ZHOU, Q., YANG, G., and WANG, G. Quartz crystal based sensor head design and analysis for robot torque sensor application. Cobot, 1, 11 (2022) |
| [18] | MUROZAKI, Y., SAKUMA, S., and ARAI, F. Improvement of the measurement range and temperature characteristics of a load sensor using a quartz crystal resonator with all crystal layer components. Sensors, 17, 1067 (2017) |
| [19] | WATANABE, S., MUROZAKI, Y., SUGIURA, H., SATO, Y., HONBE, K., and ARAI, F. Non-invasive biosignals detection for continuous monitoring of a neonate using quartz crystal resonator. Sensors and Actuators A: Physical, 317, 112475 (2021) |
| [20] | MA, L. X., YUAN, J. C., ZHOU, Q., WANG, J., and YI, L. J. Force frequency coefficient of rectangle quartz crystal resonators based load sensor. 2022 16th Symposium on Piezoelectricity, Acoustic Waves, and Device Applications (SPAWDA), IEEE, Nanjing (2022) |
| [21] | ZHOU, Y. H., CHEN, C. Y., ZHANG, L. C., CHENG, J. G., ZHOU, Q., CHAO, M. C., and WANG, Y. Research on force-frequency coefficient of square quartz crystal with encapsulation body. IEEE Sensors Journal, 23, 13469–13477 (2023) |
| [22] | YANG, G., HUANG, X., TAN, K., CHEN, Q., and PAN, W. Study of force-frequency characteristics in AT-cut strip quartz crystal resonators with different rotation angles. Sensors, 23, 2996 (2023) |
| [23] | MOHAMMADI, M. M. and HAMEDI, M. Force frequency effect in square quartz crystals. AUT Journal of Mechanical Engineering, 5, 215–226 (2021) |
| [24] | NARUMI, K., FUKUDA, T., and ARAI, F. Design and characterization of load sensor with AT-cut QCR for miniaturization and resolution improvement. Journal of Robotics and Mechatronics, 22, 286–292 (2010) |
| [25] | CHEN, F. B., GAO, J. C., and TIAN, W. J. Force-frequency characteristics of multi-electrode quartz crystal resonator cluster. Sensors and Actuators A3: Physical, 269, 427–434 (2018) |
| [26] | WANG, Z. Y., ZHU, H. Z., DONG, Y. G., and FENG, G. P. Development of a high-resolution quartz resonator force and weight sensor with increased reliability. IEEE/ASME Transactions on Mechatronics, 9, 399–406 (2004) |
| [27] | PHAM, T. T., ZHANG, H., YENUGANTI, S., KALUVAN, S., and KOSINSKI, J. A. Design, modeling, and experiment of a piezoelectric pressure sensor based on a thickness-shear-mode crystal resonator. IEEE Transactions on Industrial Electronics, 64, 8484–8491 (2017) |
| [28] | BALLATO, A. D. Effects of initial stress in vibrating quartz plates. Proceedings of the IRE, 48, 261–262 (1960) |
| [29] | JANIAUD, D., NISSIM, L., and GAGNEPAIN, J. Analytical calculation of initial stress effects on anisotropic crystals: application to quartz resonators. 32nd Annual Symposium on Frequency Control, IEEE, New Jersey (1978) |
| [30] | RATAJSKI, J. Force-frequency coefficient of singly rotated vibrating quartz crystals. IBM Journal of Research and Development, 12, 92–99 (1968) |
| [31] | MOHAMMADI, M. M. and HAMEDI, M. Experimental and numerical investigation of force-frequency effect in crystal resonators. Journal of Vibroengineering, 18, 3709–3718 (2016) |
| [32] | GOEL, N. Applications of Micromachined Quartz Resonators for Pressure and Stress Sensing, Ph. D. dissertation, The Pennsylvania State University, 1–169 (2018) |
| [33] | LEE, P. C. Y., WANG, Y. S., and MARKENSCOFF, X. High-frequency vibrations of crystal plates under initial stresses. The Journal of the Acoustical Society of America, 57, 95–105 (1975) |
| [34] | BECHMANN, R. Elastic and piezoelectric constants of alpha-quartz. Physical Review, 110, 1060–1061 (1958) |
| [35] | WANG, J., YU, J. D., YONG, Y. K., and IMAI, T. A finite element analysis of frequency-temperature relations of AT-cut quartz crystal resonators with higher-order Mindlin plate theory. Acta Mechanica, 199, 117–130 (2008) |
| [36] | BAKER, G., PAVLOVIĆ, M., and TAHAN, N. An exact solution to the two-dimensional elasticity problem with rectangular boundaries under arbitrary edge forces. Philosophical Transactions of the Royal Society of London. Series A: Physical and Engineering Sciences, 343, 307–336 (1993) |
| [37] | MOHAMMADI, M. M., DANESHPAJOOH, H., and HAMEDI, M. Effect of anisotropy and piezoelectricity on the force-frequency coeffcient of AT-cut quartz crystals. Scientia Iranica, 23, 2203–2210 (2016) |
| [38] | NARUMI, K., FUKUDA, T., and ARAI, F. Miniaturization of a wide range load sensor using AT-cut quartz crystal resonator. 2009 International Symposiumon Micro-Nano Mechatronics and Human Science, IEEE, Nagoya (2009) |
| [39] | NARUMI, K., ASAKURA, A., FUKUDA, T., and ARAI, F. Compact force sensor using AT-cut quartz crystal resonator supported by novel retention mechanism. Journal of Robotics and Mechatronics, 21, 260–266 (2009) |
| [40] | LIN, Y., ASAKURA, A., FUKUDA, T., and ARAI, F. Design and fabrication of miniaturized force sensor with quartz crystal resonators. 2007 IEEE/RSJ International Conference on Intelligent Robots and Systems, IEEE, San Diego (2007) |
| [41] | MUROZAKI, Y. and ARAI, F. Wide range load sensor using quartz crystal resonator for detection of biological signals. IEEE Sensors Journal, 15, 1913–1919 (2015) |
| [42] | YUAN, J. C., MA, C., FU, H., ZHOU, Q., and YI, L. J. Analysis of ultimate bearing capacity of quartz crystal based load sensor. 2022 16th Symposium on Piezoelectricity, Acoustic Waves, and Device Applications (SPAWDA), IEEE, Nanjing (2022) |
| [1] | Jiemin XIE, Yuantai HU. Electric admittance analysis of quartz crystal resonator in thickness-shear mode induced by array of surface viscoelastic micro-beams [J]. Applied Mathematics and Mechanics (English Edition), 2017, 38(1): 29-38. |
| [2] | Xuan XIE;Lingcheng KONG;Yuxi WANG;Jun ZHANG;Yuantai HU. Coupled vibrations and frequency shift of compound system consisting of quartz crystal resonator in thickness-shear motions and micro-beam array immersed in liquid [J]. Applied Mathematics and Mechanics (English Edition), 2015, 36(2): 225-232. |
| [3] | HUANG De-jin;DING Hao-jiang;CHEN Wei-qiu. Analytical solution for functionally graded anisotropic cantilever beam subjected to linearly distributed load [J]. Applied Mathematics and Mechanics (English Edition), 2007, 28(7): 855-860 . |
| Viewed | ||||||
|
Full text |
|
|||||
|
Abstract |
|
|||||


 Email Alert
Email Alert RSS
RSS