Applied Mathematics and Mechanics (English Edition) ›› 2025, Vol. 46 ›› Issue (10): 1955-1966.doi: https://doi.org/10.1007/s10483-025-3309-8
Previous Articles Next Articles
Received:2025-06-04
Revised:2025-09-05
Published:2025-09-30
Contact:
P. SCHIAVONE, E-mail: p.schiavone@ualberta.caSupported by:2010 MSC Number:
Xu WANG, P. SCHIAVONE. Two interacting harmonic non-elliptical compressible liquid inclusions. Applied Mathematics and Mechanics (English Edition), 2025, 46(10): 1955-1966.
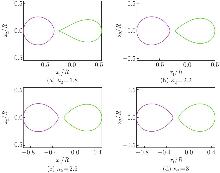
Fig. 4
The harmonic non-elliptical shapes of the two liquid-solid interfaces L1 and L2 based on Eq. (29) with Λ=−(κ2−1)/2, ρ=0.05, m=0, and λ=ρ−1/4=2.114 7. The left liquid inclusion is infinitely compressible, and the right liquid inclusion is incompressible (i.e., β1=∞, and β3=0) (color online)"
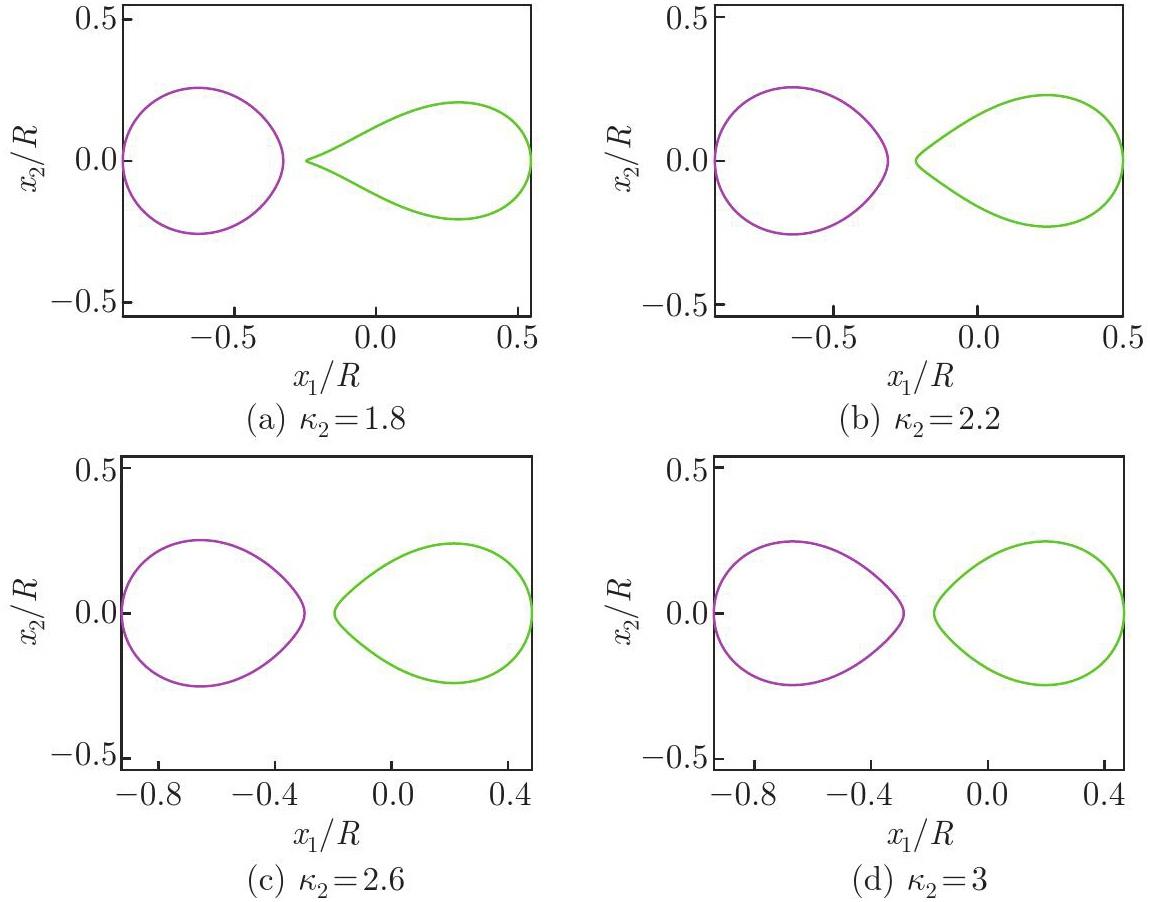
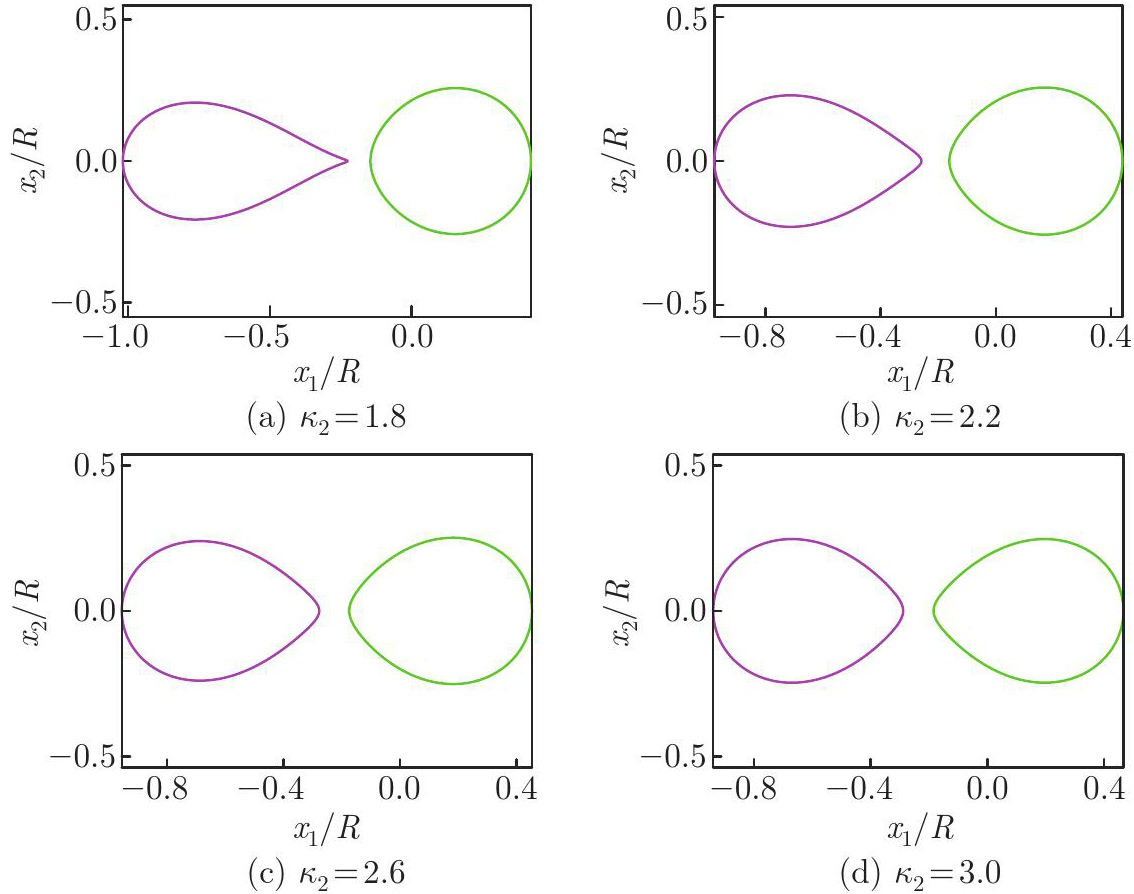
Fig. 5
The harmonic non-elliptical shapes of the two liquid-solid interfaces L1 and L2 based on Eq. (29) with Λ=−2/(κ2−1), ρ=0.05, m=0, and λ=ρ−1/4=2.114 7. The left liquid inclusion is incompressible, and the right liquid inclusion is infinitely compressible (i.e., β1=0, and β3=∞) (color online)"
| [1] | BJORKMAN, G. S. and RICHARDS, R. Harmonic holes — an inverse problem in elasticity. ASME Journal of Applied Mechanics, 43, 414–418 (1976) |
| [2] | BJORKMAN, G. S. and RICHARDS, R. Harmonic holes for nonconstant fields. ASME Journal of Applied Mechanics, 46, 573–576 (1979) |
| [3] | RICHARDS, R. and BJORKMAN, G. S. Harmonic shapes and optimum design. Journal of the Engineering Mechanics Division, 106, 1125–1134 (1980) |
| [4] | WHEELER, L. T. and KUNIN, I. A. On voids of minimum stress concentration. International Journal of Solids and Structures, 18, 85–89 (1982) |
| [5] | ELDIWANY, B. H. and WHEELER, L. T. A three-dimensional inverse problem for inhomogeneities in elastic solids. Journal of Elasticity, 16, 201–211 (1986) |
| [6] | BJORKMAN, G. S. Design of pressure vessel pads and attachments to minimize global stress concentrations. Transactions, SMiRT 19, Toronto (2007) |
| [7] | RU, C. Q. Three-phase elliptical inclusions with internal uniform hydrostatic stresses. Journal of the Mechanics and Physics of Solids, 47, 259–273 (1999) |
| [8] | RU, C. Q. A new method for an inhomogeneity with stepwise graded interphase under thermomechanical loadings. Journal of Elasticity, 56, 107–127 (1999) |
| [9] | WANG, G. F., SCHIAVONE, P., and RU, C. Q. Harmonic shapes in finite elasticity under nonuniform loading. ASME Journal of Appliled Mechanics, 72, 691–694 (2005) |
| [10] | WANG, X. Uniform fields inside two non-elliptical inclusions. Mathematics and Mechanics of Solids, 17, 736–761 (2012) |
| [11] | WANG, X. and SCHIAVONE, P. Harmonic ellipsoidal elastic solid or liquid inclusions. Journal of Elasticity, 157, 61 (2025) |
| [12] | STYLE, R. W., WETTLAUFER, J. S., and DUFRESNE, E. R. Surface tension and the mechanics of liquid inclusions in compliant solids. Soft Matter, 11, 672–679 (2015) |
| [22] | TI, F., CHEN, X., LI, M. X., SUN, X. C., LIU, S. B., and LU, T. J. Cylindrical compressible liquid inclusion with surface effects. Journal of the Mechanics and Physics of Solids, 161, 104813 (2022) |
| [23] | GHOSH, K. and LOPEZ-PAMIES, O. Elastomers filled with liquid inclusions: theory, numerical implementation, and some basic results. Journal of the Mechanics and Physics of Solids, 166, 104930 (2022) |
| [24] | GHOSH, K., LEFÈVRE, V., and LOPEZ-PAMIES, O. The effective shear modulus of a random isotropic suspension of monodisperse liquid n-spheres: from the dilute limit to the percolation threshold. Soft Matter, 19, 208–224 (2023) |
| [25] | GHOSH, K., LEFEVRE, V., and LOPEZ-PAMIES, O. Homogenization of elastomers filled with liquid inclusions: the small-deformation limit. Journal of Elasticity, 154, 235–253 (2023) |
| [26] | WANG, X. and SCHIAVONE, P. An edge dislocation interacting with an elliptical incompressible liquid inclusion. Journal of Mechanics of Materials and Structures, 19(1), 131–140 (2024) |
| [27] | WANG, X. and SCHIAVONE, P. An edge dislocation interacting with a hypotrochoidal compressible liquid inclusion. Acta Mechanica, 235, 3211–3218 (2024) |
| [28] | CHEREPANOV, G. P. Inverse problem of the plane theory of elasticity. Journal of Applied Mathematics and Mechanics, 38, 963–979 (1974) |
| [29] | MUSKHELISHVILI, N. I. Some Basic Problems of the Mathematical Theory of Elasticity, P. Noordhoff Ltd., Groningen (1953) |
| [30] | TING, T. C. T. Anisotropic Elasticity: Theory and Applications, Oxford University Press, New York (1996) |
| [31] | CHERAGHI, D. Geometric Complex Analysis, Lecture Notes, Imperial College London (2017) |
| [13] | STYLE, R. W., BOLTYANSKIY, R., ALLEN, B., JENSEN, K. E., FOOTE, H. P., WETTLAUFER, J. S., and DUFRESNE, E. R. Stiffening solids with liquid inclusions. Nature Physics, 11, 82–87 (2015) |
| [14] | MANCARELLA, F., STYLE, R. W., and WETTLAUFER, J. S. Interfacial tension and a three-phase generalized self-consistent theory of non-dilute soft composite solids. Soft Matter, 12, 2744–2750 (2016) |
| [15] | WU, J., RU, C. Q., and ZHANG, L. An elliptical liquid inclusion in an infinite elastic plane. Proceedings of the Royal Society A, 474(2215), 20170813 (2018) |
| [16] | CHEN, X., LI, M. X., YANG, M., LIU, S. B., GENIN, G. M., XU, F., and LU, T. J. The elastic fields of a compressible liquid inclusion. Extreme Mechanics Letters, 22, 122–130 (2018) |
| [17] | CHEN, X., LI, M., LIU, S., HE, W., and LU, T. J. Mechanics tuning of liquid inclusions via bio-coating. Extreme Mechanics Letters, 41, 101049 (2020) |
| [18] | KRICHEN, S., LIU, L. P., and SHARMA, P. Liquid inclusions in soft materials: capillary effect, mechanical stiffening and enhanced electromechanical response. Journal of the Mechanics and Physics of Solids, 127, 332–357 (2019) |
| [19] | DAI, M., HUA, J., and SCHIAVONE, P. Compressible liquid/gas inclusion with high initial pressure in plane deformation: modified boundary conditions and related analytical solutions. European Journal of Mechanics A-Solids, 82, 104000 (2020) |
| [20] | DAI, M., HUANG, C., and SCHIAVONE, P. Modified closed-form solutions for three-dimensional elastic deformations of a composite structure containing macro-scale spherical gas/liquid inclusions. Applied Mathematical Modelling, 97, 57–68 (2021) |
| [21] | TI, F., CHEN, X., YANG, H., LIU, S., and LU, T. J. A theory of mechanobiological sensation: strain amplification/attenuation of coated liquid inclusion with surface tension. Acta Mechanica Sinica, 37(1), 145–155 (2021) |
| [1] | Lei ZHANG. Mechanical effects of circular liquid inclusions inside soft matrix: role of internal pressure change and surface tension [J]. Applied Mathematics and Mechanics (English Edition), 2021, 42(4): 501-510. |
| [2] | Mengdie NIU, Jing XIA, Huadong YONG, Youhe ZHOU. Quench characteristics and mechanical responses during quench propagation in rare earth barium copper oxide pancake coils [J]. Applied Mathematics and Mechanics (English Edition), 2021, 42(2): 235-250. |
| [3] | Xu WANG, Ping YANG, P. SCHIAVONE. A screw dislocation near one open inhomogeneity and another closed inhomogeneity both permitting constant interior stresses [J]. Applied Mathematics and Mechanics (English Edition), 2021, 42(2): 173-182. |
| [4] | Lianhe LI, Xiaowei CUI, Junhong GUO. Interaction between a screw dislocation and an elliptical hole with two asymmetrical cracks in a one-dimensional hexagonal quasicrystal with piezoelectric effect [J]. Applied Mathematics and Mechanics (English Edition), 2020, 41(6): 899-908. |
| [5] | M. HAJIMOHAMADI, R. GHAJAR. An analytical solution for the stress field and stress intensity factor in an infinite plane containing an elliptical hole with two unequal aligned cracks [J]. Applied Mathematics and Mechanics (English Edition), 2018, 39(8): 1103-1118. |
| [6] | Chuan-ping ZHOU;Chao HU;F. MA;Dian-kui LIU. Dynamic stress concentrations in thick plates with two holes based on refined theory [J]. Applied Mathematics and Mechanics (English Edition), 2014, 35(12): 1591-1606. |
| [7] | Yi-zhou CHEN. Degenerate scale problem in antiplane elasticity or Laplace equation for contour shapes of triangles or quadrilaterals [J]. Applied Mathematics and Mechanics (English Edition), 2012, 33(4): 525-538. |
| [8] | GUO Jun-Hong;YUAN Ze-Shuai;LU Zi-Xin. General solutions of plane problem for power function curved cracks [J]. Applied Mathematics and Mechanics (English Edition), 2011, 32(5): 563-570. |
| [9] | CAO Xin-rong;SONG Tian-shu;LIU Dian-kui. SCATTERING OF PLANE SH-WAVE BY A CYLINDRICAL HILL OF ARBITRARY SHAPE [J]. Applied Mathematics and Mechanics (English Edition), 2001, 22(9): 1082-1089. |
| [10] | WANG Xu;SHEN Ya-peng . ANALYSIS OF A PARTIALLY DEBONDED CONDUCTING RIGID ELLIPTICAL INCLUSION IN A PIEZOELECTRIC MATRIX [J]. Applied Mathematics and Mechanics (English Edition), 2001, 22(1): 35-52. |
| [11] | ZHAO Jian-bin;LI Zi-guo . INFLUENCE OF COUPLE-STRESSES ON STRESS CONCENTRATIONS AROUND THE CAVITY [J]. Applied Mathematics and Mechanics (English Edition), 2000, 21(8): 893-900. |
| [12] | Hu Chao;Liu Diankui;Ma Xingrui;Wang Benli. ON THE STRESS CONCENTRATION IN THICK CYLINDRICAL SHELLS WITH AN ARBITRARY CUTOUT [J]. Applied Mathematics and Mechanics (English Edition), 1998, 19(5): 399-410. |
| [13] | Liu Diankui;Hu Chao. THE GENERAL SOLUTION FOR THE STRESS PROBLEM OF CIRCULAR CYLINDRICAL SHELLS WITH AN ARBITRARY CUTOUT [J]. Applied Mathematics and Mechanics (English Edition), 1997, 18(7): 629-646. |
| Viewed | ||||||
|
Full text |
|
|||||
|
Abstract |
|
|||||


 Email Alert
Email Alert RSS
RSS