Applied Mathematics and Mechanics (English Edition) ›› 2025, Vol. 46 ›› Issue (4): 617-632.doi: https://doi.org/10.1007/s10483-025-3233-8
Previous Articles Next Articles
Lu LU1, Min LI2, Shuang WANG3,†( )
)
Received:2025-01-04
Revised:2025-01-19
Published:2025-04-07
Contact:
Shuang WANG, E-mail: shuangwang@njtech.edu.cnSupported by:2010 MSC Number:
Lu LU, Min LI, Shuang WANG. Surface effects on buckling instability and large deformation of magneto-active soft beams. Applied Mathematics and Mechanics (English Edition), 2025, 46(4): 617-632.
Table 1
Comparison of the normalized tip deflections (δy/L) of a magneto-active cantilever beam under a uniform magnetic field"
| Ref. [ | Present | Ref. [ | Present | ||
|---|---|---|---|---|---|
| 0.362 9 | 0.362 6 | 0.710 0 | 0.710 8 | ||
| 0.659 5 | 0.661 3 | 0.806 0 | 0.805 6 | ||
| 0.805 8 | 0.804 3 | 0.752 1 | 0.752 0 | ||
| 0.854 2 | 0.851 8 | 0.639 8 | 0.639 7 | ||
| 0.887 7 | 0.883 2 | 0.502 8 | 0.502 9 | ||
| 0.901 4 | 0.895 7 | 0.397 3 | 0.397 5 | ||

Fig. 2
Normalized critical magnetic field strength as a function of the thickness of a magneto-active soft beam under a uniform magnetic field with α=π: (a) considering only surface elasticity; (b) considering only surface tension; (c) considering both surface elasticity and surface tension (color online)"


Fig. 3
Surface effects on the post-buckling behavior of magneto-active cantilever beams with L/h=20 under a uniform magnetic field with α=π: (a) normalized tip deflection as a function of dimensionless magnetic field strength for different thicknesses; (b) tip rotational angle as a function of dimensionless magnetic field strength for different thicknesses; (c) deformed configuration of magneto-active cantilever beams under a uniform magnetic field with |M||Ba|/G=0.005; (d) deformed configuration of magneto-active cantilever beams under a uniform magnetic field with |M||Ba|/G=0.02. Note that when surface effects are neglected, the post-buckling behavior of the beams is independent of its thickness with a given L/h (color online)"

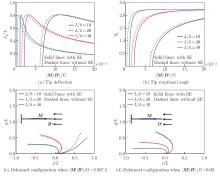
Fig. 4
Surface effects on the post-buckling behavior of magneto-active cantilever beams with h=0.2 mm under a uniform magnetic field with α=π: (a) normalized tip deflection as a function of dimensionless magnetic field strength for different length-to-thickness ratios; (b) tip rotational angle as a function of dimensionless magnetic field strength for different length-to-thickness ratios; (c) deformed configuration of magneto-active cantilever beams under a uniform magnetic field with |M||Ba|/G=0.007 5; (d) deformed configuration of magneto-active cantilever beams under a uniform magnetic field with |M||Ba|/G=0.02 (color online)"


Fig. 5
Surface effects on the large deformation of magneto-active cantilever beams with L/h=20 under a uniform magnetic field with α=π/2: (a) normalized tip deflection as a function of dimensionless magnetic field strength for different thicknesses; (b) tip rotational angle as a function of dimensionless magnetic field strength for different thicknesses; (c) deformed configuration of magneto-active cantilever beams under a uniform magnetic field with |M||Ba|/G=0.004; (d) deformed configuration of magneto-active cantilever beams under a uniform magnetic field with |M||Ba|/G=0.02. Note that when surface effects are neglected, the mechanical behavior of the beams is independent of its thickness with a given L/h (color online)"


Fig. 6
Surface effects on the large deformation of magneto-active cantilever beams with h=0.2 mm under a uniform magnetic field with α=π/2: (a) normalized tip deflection as a function of dimensionless magnetic field strength for different length-to-thickness ratios; (b) tip rotational angle as a function of dimensionless magnetic field strength for different length-to-thickness ratios; (c) deformed configuration of magneto-active cantilever beams under a uniform magnetic field with |M||Ba|/G=0.004; (d) deformed configuration of magneto-active cantilever beams under a uniform magnetic field with |M||Ba|/G=0.02 (color online)"


Fig. 7
Surface effects on the large deformation of magneto-active cantilever beams with h=0.2 mm and L/h=20 under a uniform magnetic field with 0<α⩽π/2: (a) normalized tip deflection as a function of dimensionless magnetic field strength for different α; (b) tip rotational angle as a function of dimensionless magnetic field strength for different α; (c) deformed configuration of magneto-active cantilever beams under a uniform magnetic field with |M||Ba|/G=0.004; (d) deformed configuration of magneto-active cantilever beams under a uniform magnetic field with |M||Ba|/G=0.02 (color online)"


Fig. 8
Surface effects on the large deformation of magneto-active cantilever beams with h=0.2 mm and L/h=20 under a uniform magnetic field with π/2⩽α<π: (a) normalized tip deflection as a function of dimensionless magnetic field strength for different α; (b) tip rotational angle as a function of dimensionless magnetic field strength for different α; (c) deformed configuration of magneto-active cantilever beams under a uniform magnetic field with |M||Ba|/G=0.004; (d) deformed configuration of magneto-active cantilever beams under a uniform magnetic field with |M||Ba|/G=0.02 (color online)"

| [1] | KIM, Y. and ZHAO, X. Magnetic soft materials and robots. Chemical Reviews, 122(5), 5317–5364 (2022) |
| [2] | WANG, L., ZHENG, D., HARKER, P., PATEL, A. B., GUO, C. F., and ZHAO, X. Evolutionary design of magnetic soft continuum robots. Proceedings of the National Academy of Sciences, 118(21), e2021922118 (2021) |
| [3] | HU, W., LUM, G. Z., MASTRANGELI, M., and SITTI, M. Small-scale soft-bodied robot with multimodal locomotion. nature, 554(7690), 81–85 (2018) |
| [4] | ZHANG, Q., CHERKASOV, A. V., XIE, C., ARORA, N., and RUDYKH, S. Nonlinear elastic vector solitons in hard-magnetic soft mechanical metamaterials. International Journal of Solids and Structures, 280, 112396 (2023) |
| [5] | CHEN, T., PAULY, M., and REIS, P. M. A reprogrammable mechanical metamaterial with stable memory. nature, 589(7842), 386–390 (2021) |
| [6] | ALAPAN, Y., KARACAKOL, A. C., GUZELHAN, S. N., ISIK, I., and SITTI, M. Reprogrammable shape morphing of magnetic soft machines. Science Advances, 6(38), eabc6414 (2020) |
| [7] | CUI, J., HUANG, T. Y., LUO, Z., TESTA, P., GU, H., CHEN, X. Z., NELSON, B. J., and HEYDERMAN, L. J. Nanomagnetic encoding of shape-morphing micromachines. nature, 575(7781), 164–168 (2019) |
| [8] | LUM, G. Z., YE, Z., DONG, X., MARVI, H., ERIN, O., HU, W., and SITTI, M. Shape-programmable magnetic soft matter. Proceedings of the National Academy of Sciences, 113(41), E6007-E6015 (2016) |
| [9] | YAN, D., ABBASI, A., and REIS, P. M. A comprehensive framework for hard-magnetic beams: reduced-order theory, 3D simulations, and experiments. International Journal of Solids and Structures, 257, 111319 (2022) |
| [10] | WANG, L., KIM, Y., GUO, C. F., and ZHAO, X. Hard-magnetic elastica. Journal of the Mechanics and Physics of Solids, 142, 104045 (2020) |
| [11] | YANG, Y., LI, M., and XU, F. A 3D hard-magnetic rod model based on co-rotational formulations. Acta Mechanica Sinica, 38(9), 222085 (2022) |
| [12] | CHEN, W., YAN, Z., and WANG, L. On mechanics of functionally graded hard-magnetic soft beams. International Journal of Engineering Science, 157, 103391 (2020) |
| [13] | CHEN, W. and WANG, L. Theoretical modeling and exact solution for extreme bending deformation of hard-magnetic soft beams. Journal of Applied Mechanics, 87(4), 041002 (2020) |
| [14] | CHEN, W., WANG, G., LI, Y., WANG, L., and YIN, Z. The quaternion beam model for hard-magnetic flexible cantilevers. Applied Mathematics and Mechanics (English Edition), 44(5), 787–808 (2023) https://doi.org/10.1007/s10483-023-2983-8 |
| [15] | TAN, K., CHEN, L., YANG, S., and DENG, Q. Dynamic snap-through instability and damped oscillation of a flat arch of hard magneto-active elastomers. International Journal of Mechanical Sciences, 230, 107523 (2022) |
| [16] | DEHROUYEH-SEMNANI, A. M. On bifurcation behavior of hard magnetic soft cantilevers. International Journal of Non-Linear Mechanics, 134, 103746 (2021) |
| [17] | XING, Z. and YONG, H. Numerical study on the instabilities of hard-magnetic soft materials with viscoelastic effects. Mechanics of Materials, 179, 104602 (2023) |
| [18] | PEZZULLA, M., YAN, D., and REIS, P. M. A geometrically exact model for thin magneto-elastic shells. Journal of the Mechanics and Physics of Solids, 166, 104916 (2022) |
| [19] | YAN, D., AYMON, B. F., and REIS, P. M. A reduced-order, rotation-based model for thin hard-magnetic plates. Journal of the Mechanics and Physics of Solids, 170, 105095 (2023) |
| [20] | MILLER, R. E. and SHENOY, V. B. Size-dependent elastic properties of nanosized structural elements. Nanotechnology, 11(3), 139 (2000) |
| [21] | JING, G., DUAN, H. L., SUN, X., ZHANG, Z., XU, J., LI, Y., WANG, J., and YU, D. Surface effects on elastic properties of silver nanowires: contact atomic-force microscopy. Physical Review B—Condensed Matter and Materials Physics, 73(23), 235409 (2006) |
| [22] | STYLE, R. W., HYLAND, C., BOLTYANSKIY, R., WETTLAUFER, J. S., and DUFRESNE, E. R. Surface tension and contact with soft elastic solids. Nature Communications, 4(1), 2728 (2013) |
| [23] | MORA, S., PHOU, T., FROMENTAL, J. M., PISMEN, L. M., and POMEAU, Y. Capillarity driven instability of a soft solid. Physical Review Letters, 105(21), 214301 (2010) |
| [24] | GURTIN, M. E. and MURDOCH, A. I. A continuum theory of elastic material surfaces. Archive for Rational Mechanics and Analysis, 57, 291–323 (1975) |
| [25] | GURTIN, M. E. and MURDOCH, A. I. Surface stress in solids. International Journal of Solids and Structures, 14(6), 431–440 (1978) |
| [26] | WANG, S., LI, X., YI, X., and DUAN, H. Morphological changes of nanofiber cross-sections due to surface tension. Extreme Mechanics Letters, 44, 101211 (2021) |
| [27] | LU, P., HE, L., LEE, H., and LU, C. Thin plate theory including surface effects. International Journal of Solids and Structures, 43(16), 4631–4647 (2006) |
| [28] | LI, M., ZHANG, H. X., ZHAO, Z. L., and FENG, X. Q. Surface effects on cylindrical indentation of a soft layer on a rigid substrate. Acta Mechanica Sinica, 36, 422–429 (2020) |
| [29] | LI, M., YAN, Y., XU, S., WANG, G., WU, J., and FENG, X. Q. Surface effect on the necking of hyperelastic materials. Current Applied Physics, 38, 91–98 (2022) |
| [30] | WANG, G. F. and FENG, X. Q. Effects of surface elasticity and residual surface tension on the natural frequency of microbeams. Applied Physics Letters, 90(23), 231904 (2007) |
| [31] | WANG, G. F. and FENG, X. Q. Surface effects on buckling of nanowires under uniaxial compression. Applied Physics Letters, 94(14), 141913 (2009) |
| [32] | HE, J. and LILLEY, C. M. Surface effect on the elastic behavior of static bending nanowires. Nano Letters, 8(7), 1798–1802 (2008) |
| [33] | WANG, Q., LIU, M., WANG, Z., CHEN, C., and WU, J. Large deformation and instability of soft hollow cylinder with surface effects. Journal of Applied Mechanics, 88(4), 041010 (2021) |
| [34] | ZHANG, L., ZHAO, J., NIE, G., and LIU, J. Propagation of Rayleigh-type surface waves in a layered piezoelectric nanostructure with surface effects. Applied Mathematics and Mechanics (English Edition), 43(3), 327–340 (2022) https://doi.org/10.1007/s10483-022-2824-7 |
| [35] | FENG, X., KE, L., and GAO, Y. Love wave propagation in one-dimensional piezoelectric quasicrystal multilayered nanoplates with surface effects. Applied Mathematics and Mechanics (English Edition), 45(4), 619–632 (2024) https://doi.org/10.1007/s10483-024-3104-9 |
| [36] | DUAN, H., WANG, J., and KARIHALOO, B. L. Theory of elasticity at the nanoscale. Advances in Applied Mechanics, 42, 1–68 (2009) |
| [37] | CHEN, G. Y., THUNDAT, T., WACHTER, E., and WARMACK, R. Adsorption-induced surface stress and its effects on resonance frequency of microcantilevers. Journal of Applied Physics, 77(8), 3618–3622 (1995) |
| [38] | LU, P., SHEN, F., SHEA, S. O., LEE, K., and NG, T. Analysis of surface effects on mechanical properties of microcantilevers. Materials Physics and Mechanics, 4, 51–55 (2001) |
| [39] | XU, Q., JENSEN, K. E., BOLTYANSKIY, R., SARFATI, R., STYLE, R. W., and DUFRESNE, E. R. Direct measurement of strain-dependent solid surface stress. Nature Communications, 8(1), 555 (2017) |
| [40] | SORIANO-JEREZ, Y., GOURLAOUEN, E., ZERIOUH, O., CERÓN-GARCÍA, M. D., ARRABAL-CAMPOS, F. M., RUIZ-MARTÍNEZ, C., FERNÁNDEZ, I., GALLARDO-RODRÍGUEZ, J. J., GARCÍA-CAMACHO, F., and MOLINA-GRIMA, E. Role of dynamic surface tension of silicone polyether surfactant-based silicone coatings on protein adsorption: an insight on the ‘ambiguous’ interfacial properties of fouling release coatings. Progress in Organic Coatings, 186, 108079 (2024) |
| [41] | SCHULTZ, C. W., NG, C. L., and YU, H. Z. Superhydrophobic polydimethylsiloxane via nanocontact molding of solvent crystallized polycarbonate: optimized fabrication, mechanistic investigation, and application potential. ACS Applied Materials & Interfaces, 12(2), 3161–3170 (2019) |
| [42] | LI, S., ZHANG, J., HE, J., LIU, W., WANG, Y., HUANG, Z., PANG, H., and CHEN, Y. Functional PDMS elastomers: bulk composites, surface engineering, and precision fabrication. Advanced Science, 10(34), 2304506 (2023) |
| [1] | Xin FENG, Liaoliang KE, Yang GAO. Love wave propagation in one-dimensional piezoelectric quasicrystal multilayered nanoplates with surface effects [J]. Applied Mathematics and Mechanics (English Edition), 2024, 45(4): 619-632. |
| [2] | Yunzhi HUANG, Wenqing ZHENG, Xiuhua CHEN, Miaolin FENG. Analytic solution of quasicrystal microsphere considering the thermoelectric effect and surface effect in the elastic matrix [J]. Applied Mathematics and Mechanics (English Edition), 2023, 44(8): 1331-1350. |
| [3] | Wei CHEN, Guozhen WANG, Yiqun LI, Lin WANG, Zhouping YIN. The quaternion beam model for hard-magnetic flexible cantilevers [J]. Applied Mathematics and Mechanics (English Edition), 2023, 44(5): 787-808. |
| [4] | Biao HU, Juan LIU, Yuxing WANG, Bo ZHANG, Jing WANG, Huoming SHEN. Study on wave dispersion characteristics of piezoelectric sandwich nanoplates considering surface effects [J]. Applied Mathematics and Mechanics (English Edition), 2022, 43(9): 1339-1354. |
| [5] | Wenjun WANG, Feng JIN, Tianhu HE, Yongbin MA. Nonlinear magneto-mechanical-thermo coupling characteristic analysis for transport behaviors of carriers in composite multiferroic piezoelectric semiconductor nanoplates with surface effect [J]. Applied Mathematics and Mechanics (English Edition), 2022, 43(9): 1323-1338. |
| [6] | M. FARAJI-OSKOUIE, R. ANSARI, M. DARVIZEH. A variational differential quadrature solution to finite deformation problems of hyperelastic shell-type structures: a two-point formulation in Cartesian coordinates [J]. Applied Mathematics and Mechanics (English Edition), 2022, 43(8): 1219-1232. |
| [7] | Lele ZHANG, Jing ZHAO, Guoquan NIE, Jinxi LIU. Propagation of Rayleigh-type surface waves in a layered piezoelectric nanostructure with surface effects [J]. Applied Mathematics and Mechanics (English Edition), 2022, 43(3): 327-340. |
| [8] | Ye XIAO, J. SHANG, L. Z. KOU, Chun LI. Surface deformation-dependent mechanical properties of bending nanowires: an ab initio core-shell model [J]. Applied Mathematics and Mechanics (English Edition), 2022, 43(2): 219-232. |
| [9] | Shunzu ZHANG, Qianqian HU, Wenjuan ZHAO. Surface effect on band structure of magneto-elastic phononic crystal nanoplates subject to magnetic and stress loadings [J]. Applied Mathematics and Mechanics (English Edition), 2022, 43(2): 203-218. |
| [10] | Zhina ZHAO, Junhong GUO. Surface effects on a mode-III reinforced nano-elliptical hole embedded in one-dimensional hexagonal piezoelectric quasicrystals [J]. Applied Mathematics and Mechanics (English Edition), 2021, 42(5): 625-640. |
| [11] | Denghui QIAN. Electro-mechanical coupling wave propagating in a locally resonant piezoelectric/elastic phononic crystal nanobeam with surface effects [J]. Applied Mathematics and Mechanics (English Edition), 2020, 41(3): 425-438. |
| [12] | Nan NAN, Guohui HU. Morphology of cylindrical cell sheets with embedded contractile ring [J]. Applied Mathematics and Mechanics (English Edition), 2019, 40(12): 1847-1860. |
| [13] | Xin LIN, Yixin HUANG, Yang ZHAO, Tianshu WANG. Large deformation analysis of a cantilever beam made of axially functionally graded material by homotopy analysis method [J]. Applied Mathematics and Mechanics (English Edition), 2019, 40(10): 1375-1386. |
| [14] | H. S. ZHAO, Y. ZHANG, S. T. LIE. Frequency equations of nonlocal elastic micro/nanobeams with the consideration of the surface effects [J]. Applied Mathematics and Mechanics (English Edition), 2018, 39(8): 1089-1102. |
| [15] | Yanmei YUE, Kaiyu XU, Xudong ZHANG, Wenjing WANG. Effect of surface stress and surface-induced stress on behavior of piezoelectric nanobeam [J]. Applied Mathematics and Mechanics (English Edition), 2018, 39(7): 953-966. |
| Viewed | ||||||
|
Full text |
|
|||||
|
Abstract |
|
|||||


 Email Alert
Email Alert RSS
RSS