Fig. 1

Schematic illustration of a curved beam with boundary axial constraints: (a) the non-zero axial constraint with the end spring stiffness/mass; (b) the vanishing axial constraint (i.e., free to move) (color online)"

Fig. 2

Kinematic illustration for the beam's large-amplitude motion (color online)"

Fig. 3

Kinematic illustration of motion and deformation for the beam's cross-section (color online)"

Table 1

Parameters of a straight inextensible beam "

Fig. 4

Time history responses: approximate analytical (perturbation) results and numerical results when $ \mu_{\rm l}=0, k_{\rm l}=30, F=0.1, c=0.06, a(0)=0.036\, 0 $, and $ \gamma(0)=0.440\, 4 $ (color online)"

Fig. 5

Competition of inertial nonlinearity and geometric nonlinearity: (a) geometric nonlinearity dominates hardening dynamics (combined FRC in red) and (b) inertial nonlinearity dominates softening dynamics (combined FRC in red) (color online)"

Fig. 6

Analysis of softening/hardening transition with respect to the end stiffness ratio $ k_{\rm l} $, where solid lines represent stable configurations, and dashed lines represent unstable configurations with $ c=0.02 $ and $ F=0.03 $: (a) the effective nonlinear coefficient $ \Gamma_{\rm n} $ and (b) the representative FRCs (softening in blue, hardening in red, and linear symmetry in black) (color online)"

Fig. 7

Analysis of hardening/softening transition with respect to the end mass ratio $ \mu_{\rm l} $, where solid lines represent stable configurations, and dashed lines represent unstable configurations with $ c=0.05 $ and $ F=0.05 $: (a) the effective nonlinear coefficient $ \Gamma_{\rm n} $ and (b) the representative FRCs (softening in blue, hardening in red, and linear symmetry in black) (color online)"

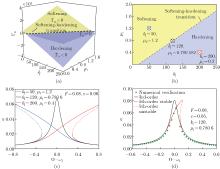
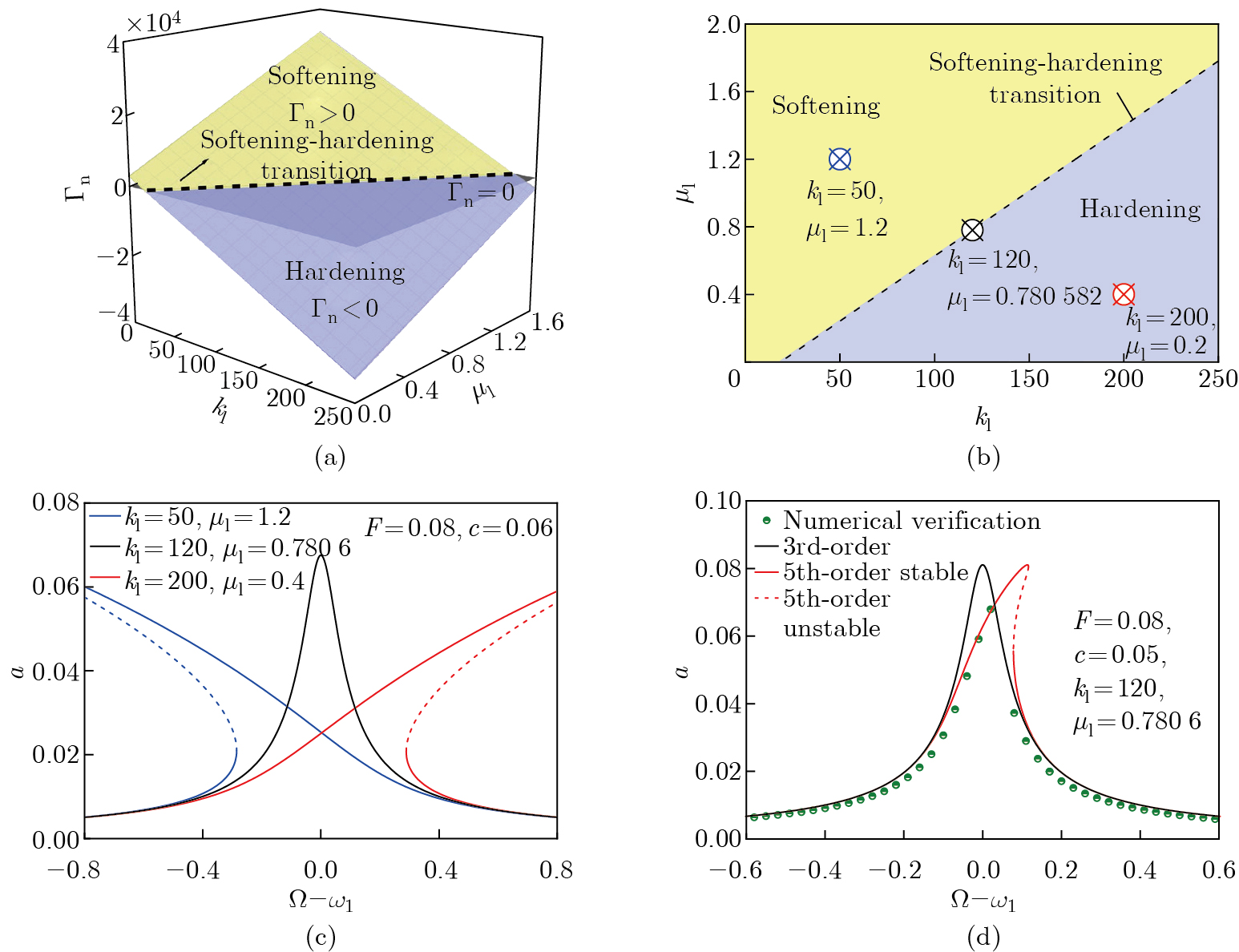
Fig. 8

Hardening/softening transition phenomenon: (a) the effective nonlinear coefficient $ \Gamma_{\rm n} $ and the hardening/softening separatrix, (b) the hardening/softening separatrix and softening vs. hardening illustrated in the two-dimensional parameter plane $ \mu_{\rm l}k_{\rm l} $, (c) three representative FRCs (softening in blue, symmetry in black, and hardening in red), and (d) corrected hardening FRC exactly on the hardening/softening separatrix, where solid lines denote stable configurations, and dashed lines denote unstable configurations (color online)"

Fig. 9

A convergence test of the multi-mode Galerkin discretized model: time history responses and phase portraits for $ b=1.0 $, $ \mu_{\rm l}=0 $, $ k_{\rm l}=100 $, $ f=10 $, $ \Omega =3.04 $, and $ q_{i}(t)=0.001 $ ($ i=1, 2, \cdots, 7 $) (zero initial velocity) (color online)"

Fig. 10

FRCs of the inextensible curved beam: (a) with different initial rises $ b $ and (b) with different boundary stiffness ratios $ k_{\rm l} $ (color online)"

Fig. 11

FRCs of the inextensible curved beam with different values of the mass ratio $ \mu_{\rm l} $ (color online)"