Applied Mathematics and Mechanics (English Edition) ›› 2025, Vol. 46 ›› Issue (6): 1143-1166.doi: https://doi.org/10.1007/s10483-025-3256-7
Previous Articles Next Articles
Xu ZHANG1, Dayang DENG1, M. YE2, T. SUMIGAWA2, H. R. MA2, Xuewei HUANG1,†(
)
Email Alert
RSSReceived:2025-02-24
Revised:2025-04-07
Published:2025-06-06
Contact:
Xuewei HUANG, E-mail: huangxw@zzu.edu.cnSupported by:2010 MSC Number:
Xu ZHANG, Dayang DENG, M. YE, T. SUMIGAWA, H. R. MA, Xuewei HUANG. Surface effects on double-ended dislocation sources in single-crystal micropillars: implications for size-dependent and stochastic yield strength. Applied Mathematics and Mechanics (English Edition), 2025, 46(6): 1143-1166.
Fig. 1
Schematic of mixed-character dislocation segment near a free surface, deriving the elastic stress field by the image force method (color online)"
Fig. 2
Schematic of real dislocation segment AB and its image segment A′B′, symmetric about the xy-plane, obtained by subtracting the semi-infinite dislocation originating at Point B from its counterpart at Point A (color online)"
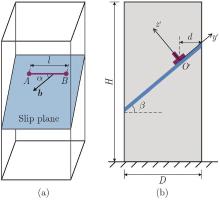
Fig. 3
Geometrical configuration of a double-ended dislocation segment AB in a single-crystal micropillar oriented for single slip: (a) three-dimensional model illustrating the spatial arrangement of dislocation source; (b) two-dimensional representation showing the projection of the dislocation segment in the slip plane (color online)"
Table 1
Summary of the material and geometric parameters"
| Variant | Symbol | Unit |
|---|---|---|
| Side length | ||
| Micropillar height | ||
| Burgers vector angle | (°) | |
| Slip angle | (°) | |
| Shear modulus | GPa | |
| Burgers vector | nm | |
| Poisson's ratio | – | |
| Segment length | nm | |
| Distance from surface | nm |
Fig. 4
Normalized surface stress τ¯gseg for edge, screw, and mixed dislocations as a function of the normalized distance dD for different normalized lengths lD. τ¯gseg plotted against (a) the logarithmic representation of entail distance 0.000 1⩽dD⩽0.5; (b) the small distance 0.001⩽dD⩽0.01; (c) the moderate distance 0.01⩽dD⩽0.1; (d) the large distance 0.1⩽dD⩽0.3 (color online)"
Fig. 5
Variations of relative stress τesegτsseg as a function of the normalized distance dD at different normalized segment lengths lD (color online)"
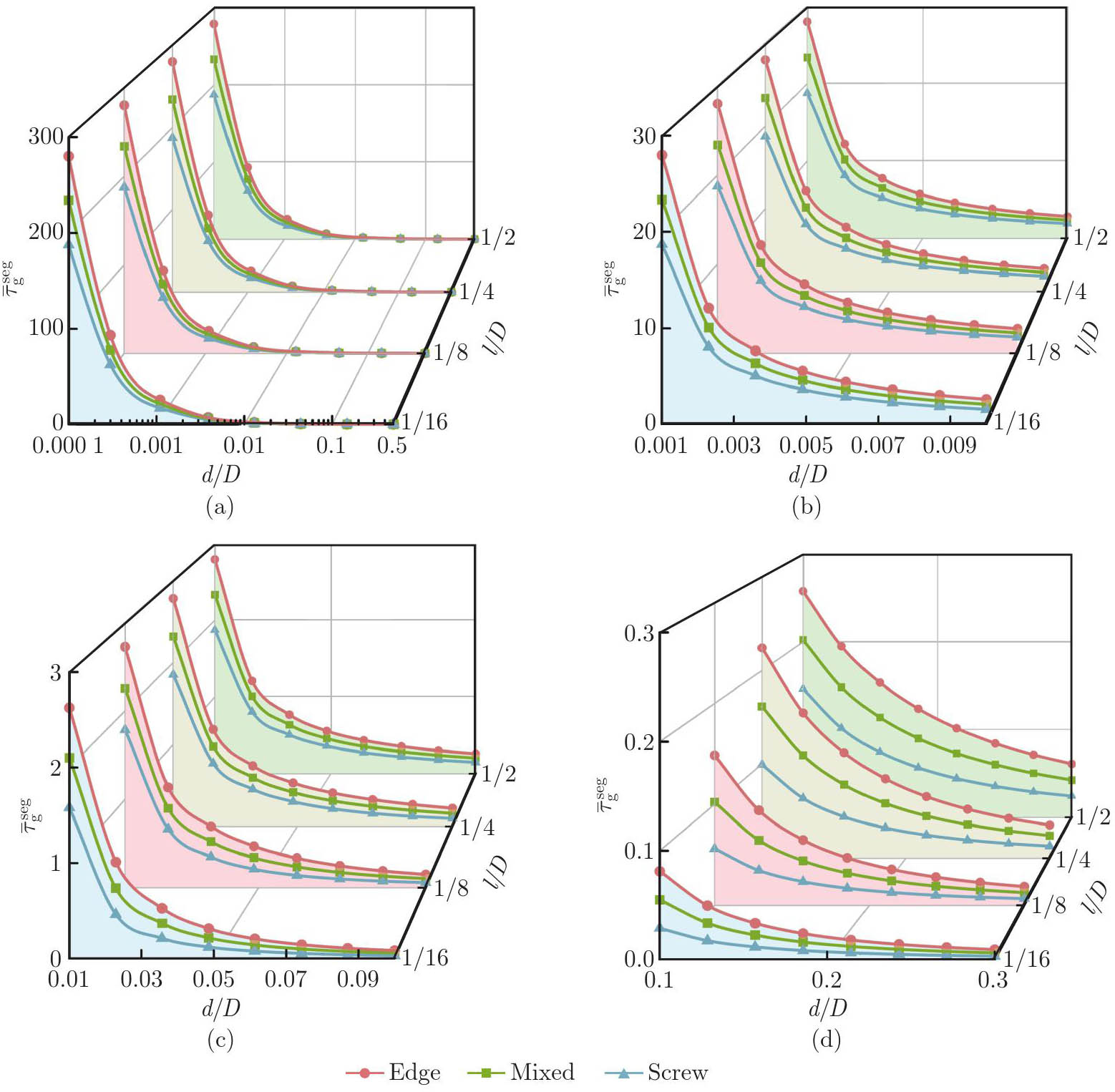
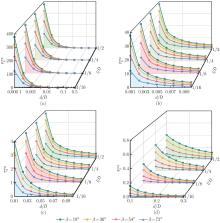
Fig. 6
Normalized surface stress τ¯gseg as a function of the normalized distance dD for various slip plane inclinations β at different normalized lengths dD. τ¯gseg plotted against (a) the logarithmic representation of entail distance 0.000 1⩽dD⩽0.5; (b) the small distance 0.001⩽dD⩽0.01; (c) the moderate distance 0.01⩽dD⩽0.1; (d) the large distance 0.1⩽dD⩽0.3 (color online)"
Fig. 7
The anisotropy ratio as a function of the normalized distance dD for various slip plane inclinations β at different normalized lengths lD (color online)"
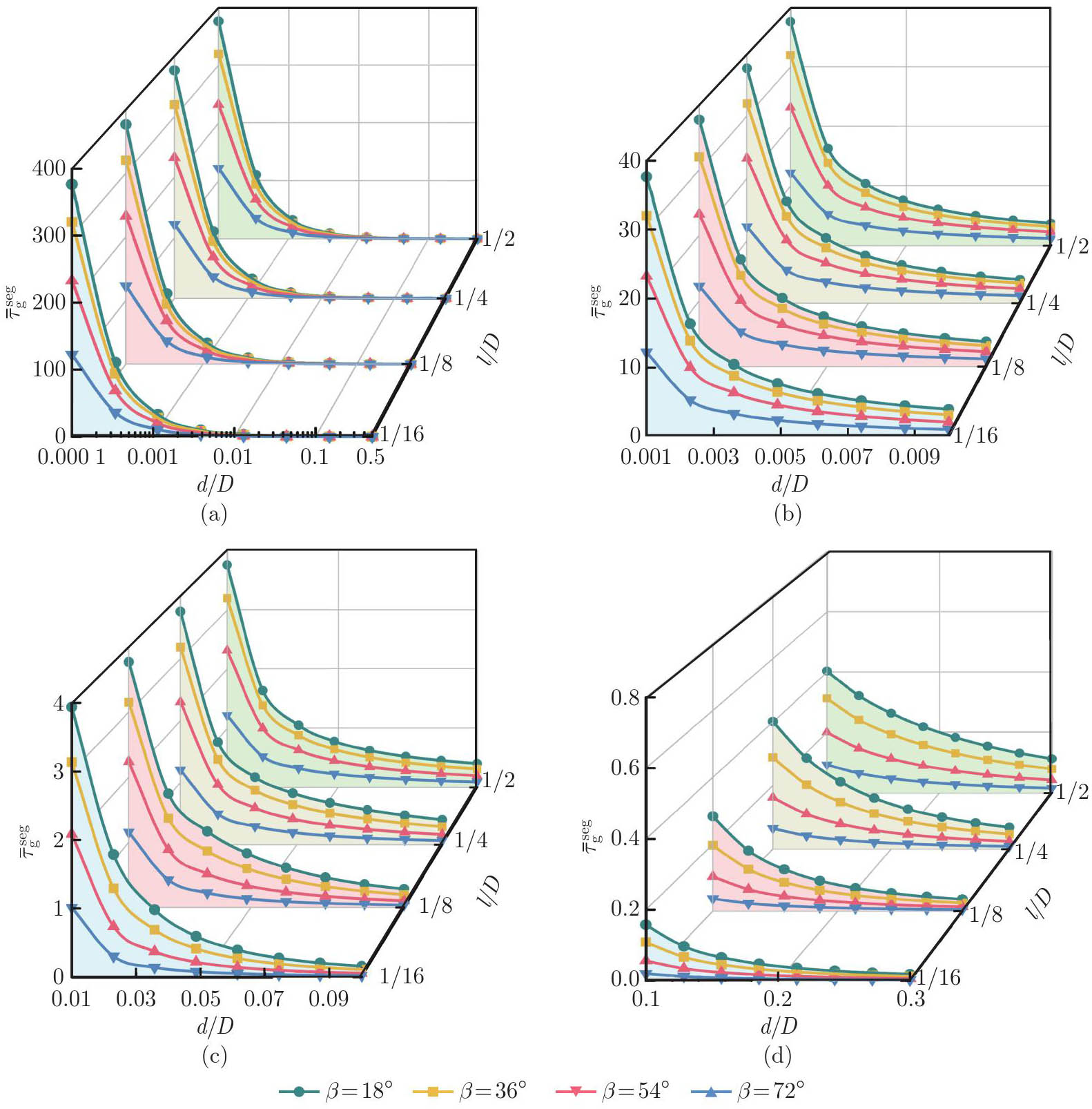
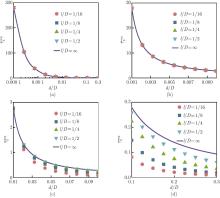
Fig. 8
Normalized surface stress τ¯gseg as a function of the normalized distance dD for different normalized lengths lD. τ¯gseg plotted against (a) the logarithmic representation of entail distance 0.000 1⩽dD⩽0.3; (b) the small distance 0.001⩽dD⩽0.01; (c) the moderate distance 0.01⩽dD⩽0.1; (d) the large distance 0.1⩽dD⩽0.3 (color online)"
Fig. 9
A comparison of the PK force fgsegfg∞ between a dislocation segment and an infinitely long dislocation as a function of the normalized dD (color online)"
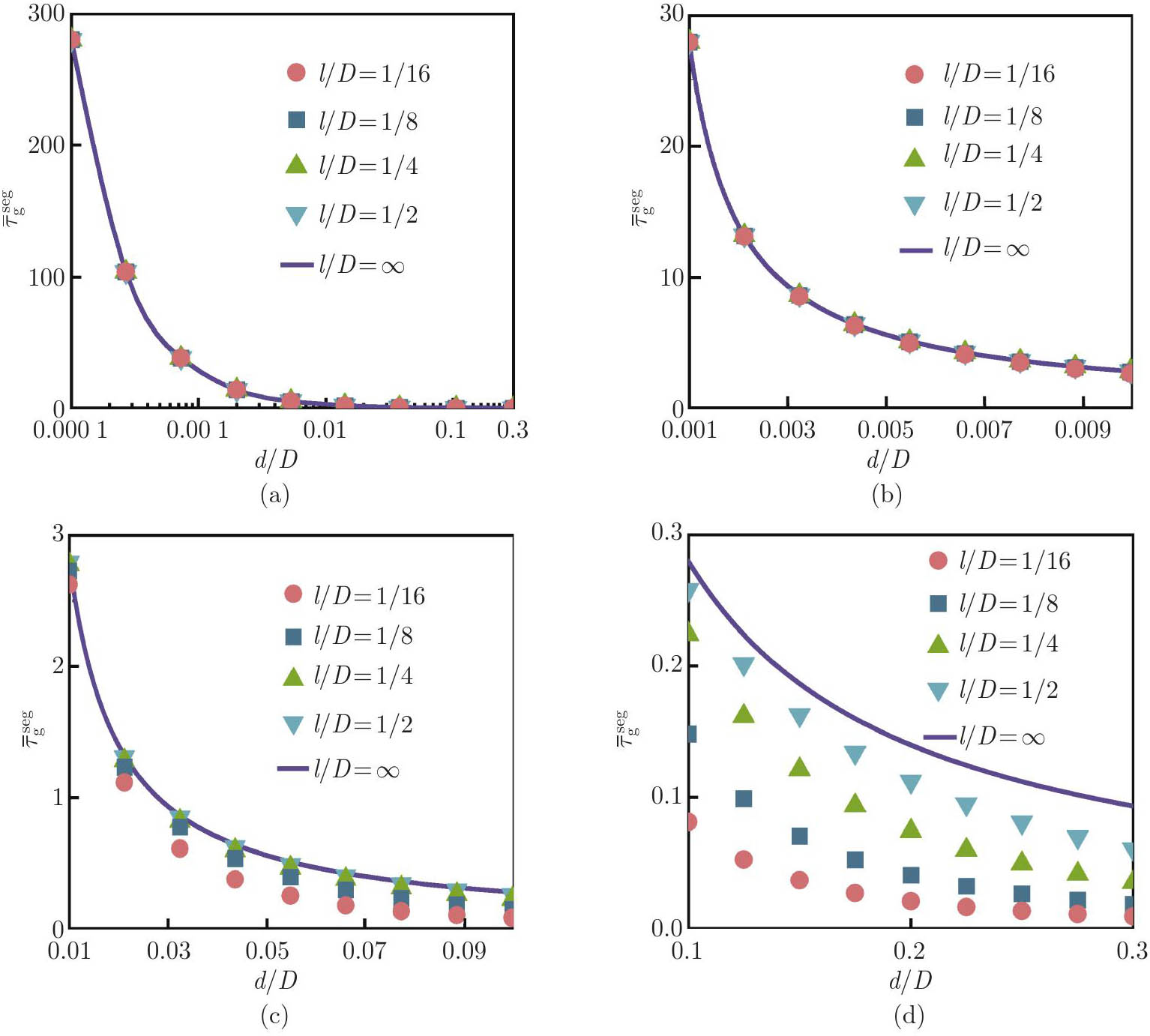
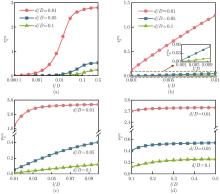
Fig. 10
Normalized surface stress τ¯gseg as a function of the normalized length lD for different normalized distances dD. τ¯gseg plotted against (a) the logarithmic representation of entail length 0.000 1⩽lD⩽0.5; (b) the small length 0.001⩽lD⩽0.01; (c) the moderate length 0.01⩽lD⩽0.1; (d) the large length 0.1⩽lD⩽0.5 (color online)"
Fig. 11
Relative PK force fgsegfg∞ as a function of the normalized length lD for different normalized distances dD. fgsegfg∞ plotted versus (a) the segment length and (b) the logarithmic representation of segment length (color online)"
Fig. 12
Relative surface stress τgseg/τg∞ at a given point as a function of the position rρ for different normalized distances dD and segment lengths lD. Four different normalized distances include (a) dD=0.000 2, (b) dD=0.002, (c) dD=0.02, and (d) dD=0.2 (color online)"
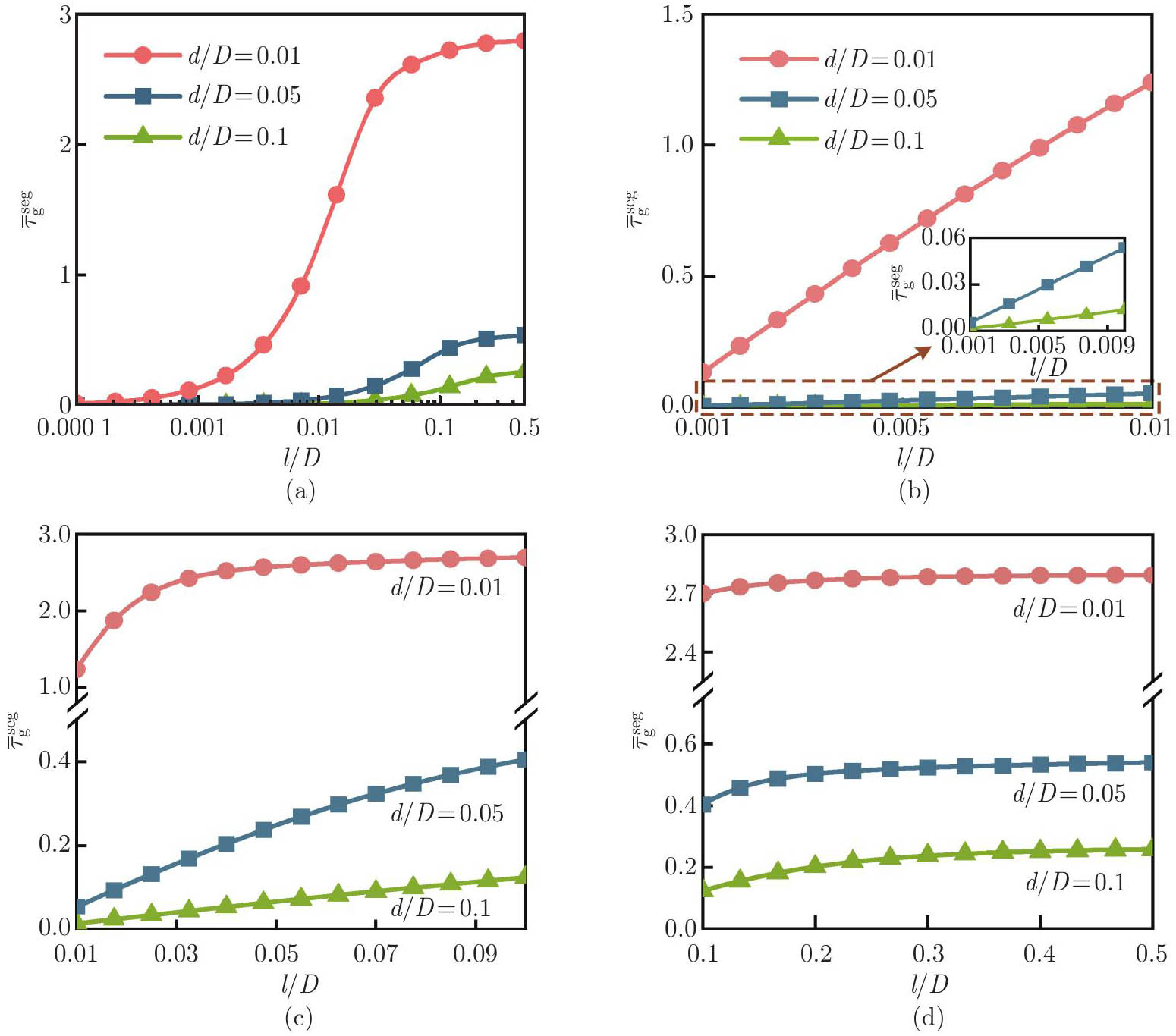
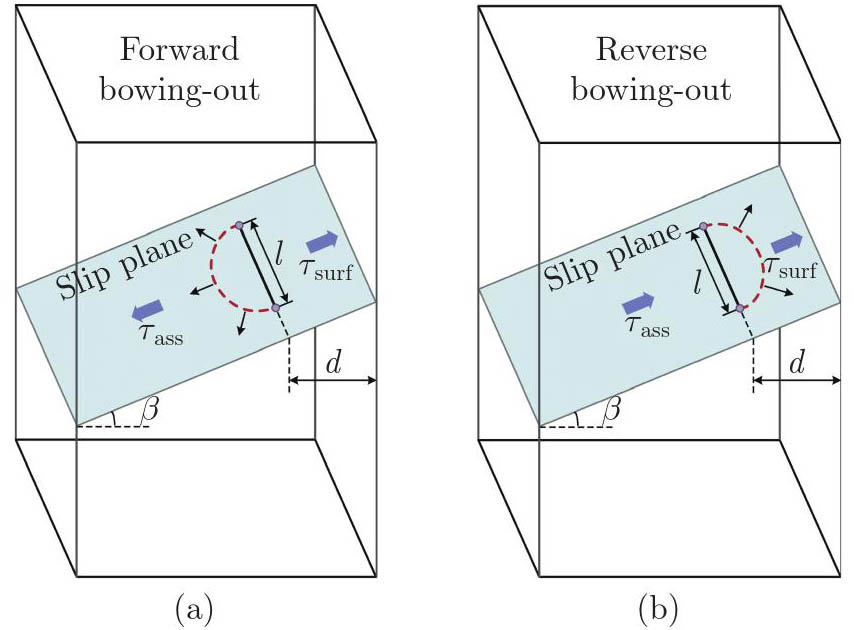
Fig. 13
A schematic illustrating the dynamic competition between the applied shear stress τass driving dislocation bow out and the surface stress pulling segment back toward the free surface. The yield strength is either enhanced or weakened depending on the (a) forward bowing-out and (b) reverse bowing-out of the FR source (color online)"
Fig. 14
The variation of source-strength coefficient αFR over a broad range of slip angles β: comparison of input values[28,57-59] and results[33] of numerical simulation (color online)"
| [1] | BEETS, N., FARKAS, D., and ALBE, K. The mechanical response of nanoporous gold and silver foams with varying composition and surface segregation. Acta Materialia, 203, 116445 (2021) |
| [2] | BAI, J. H. and WANG, S. F. Screw dislocation equations in a thin film and surface effects. International Journal of Plasticity, 87, 181-203 (2016) |
| [3] | PENG, X. L., HUSSER, E., HUANG, G. Y., and BARGMANN, S. Modeling of surface effects in crystalline materials within the framework of gradient crystal plasticity. Journal of the Mechanics and Physics of Solids, 112, 508-522 (2018) |
| [4] | BRINCKMANN, S. and SIEGMUND, T. Free-surface enhanced continuum model predicts size-effect for pillar compression at micro-and nano-scale. International Journal of Materials Research, 103, 263-270 (2012) |
| [5] | HURTADO, D. E. and ORTIZ, M. Surface effects and the size-dependent hardening and strengthening of nickel micropillars. Journal of the Mechanics and Physics of Solids, 60, 1432-1446 (2012) |
| [6] | WEINBERGER, C. R. and CAI, W. Surface-controlled dislocation multiplication in metal micropillars. Proceedings of the National Academy of Sciences of the United States of America, 105, 14304-14307 (2008) |
| [7] | LIU, Y. F., VAN DER GIESSEN, E., and NEEDLEMAN, A. An analysis of dislocation nucleation near a free surface. International Journal of Solids and Structures, 44, 1719-1732 (2007) |
| [8] | FITZGERALD, S. P. and AUBRY, S. Self-force on dislocation segments in anisotropic crystals. Journal of Physics: Condensed Matter, 22, 295403 (2010) |
| [9] | HULL, D. and BACON, D. J. Introduction to Dislocations, Elsevier, Oxford (2011) |
| [10] | ANDERSON, P. M., HIRTH, J. P., and LOTHE, J. Theory of Dislocations, Cambridge University Press, Cambridge (2017) |
| [11] | CHU, S. N. G. Screw dislocation in a two-phase isotropic thin film. Journal of Applied Physics, 53, 3019-3023 (1982) |
| [12] | LEE, S. A new analysis of elastic interaction between a surface crack and parallel screw dislocations. Engineering Fracture Mechanics, 22, 429-435 (1985) |
| [13] | HEAD, A. K. The interaction of dislocations and boundaries. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, 44, 92-94 (1953) |
| [14] | HEAD, A. K. Edge dislocations in inhomogeneous media. Proceedings of the Physical Society: Section B, 66, 793-801 (1953) |
| [15] | WEEKS, R., DUNDURS, J., and STIPPES, M. Exact analysis of an edge dislocation near a surface layer. International Journal of Engineering Science, 6, 365-372 (1968) |
| [16] | SAVAGE, J. C. Displacement field for an edge dislocation in a layered half-space. Journal of Geophysical Research: Solid Earth, 103, 2439-2446 (1998) |
| [17] | WUTTIG, M. and BIRNBAUM, H. K. Self-diffusion along edge dislocations in nickel. Physical Review, 147, 495-504 (1966) |
| [18] | YOFFE, E. H. A dislocation at a free surface. Philosophical Magazine, 6, 1147-1155 (1961) |
| [19] | MAURISSEN, Y. and CAPELLA, L. Stress field of a dislocation segment parallel to a free surface. Philosophical Magazine, 29, 1227-1229 (1974) |
| [20] | SHAIBANI, S. J. and HAZZLEDINE, P. M. The displacement and stress fields of a general dislocation close to a free surface of an isotropic solid. Philosophical Magazine A, 44, 657-665 (1981) |
| [21] | BARNETT, D. M. and LOTHE, J. An image force theorem for dislocations in anisotropic bicrystals. Journal of Physics F: Metal Physics, 4, 1618-1635 (1974) |
| [22] | WU, W., SCHÄUBLIN, R., and CHEN, J. General dislocation image stress of anisotropic cubic thin film. Journal of Applied Physics, 112, 093522 (2012) |
| [23] | LUO, S. C. and CUI, Y. N. Self-force of high-speed dislocation in anisotropic media based on configurational mechanics. International Journal of Solids and Structures, 281, 112439 (2023) |
| [24] | UCHIC, M. D., SHADE, P. A., and DIMIDUK, D. M. Plasticity of micrometer-scale single crystals in compression. Annual Review of Materials Research, 39, 361-386 (2009) |
| [25] | GREER, J. R. and DE HOSSON, J. T. M. Plasticity in small-sized metallic systems: intrinsic versus extrinsic size effect. Progress in Materials Science, 56, 654-724 (2011) |
| [26] | MOTZ, C., SCHÖBERL, T., and PIPPAN, R. Mechanical properties of micro-sized copper bending beams machined by the focused ion beam technique. Acta Materialia, 53, 4269-4279 (2005) |
| [27] | HUANG, K., SUMIGAWA, T., and KITAMURA, T. Experimental evaluation of loading mode effect on plasticity of microscale single-crystal copper. Materials Science and Engineering: A, 806, 140822 (2021) |
| [28] | TANG, H., SCHWARZ, K. W., and ESPINOSA, H. D. Dislocation escape-related size effects in single-crystal micropillars under uniaxial compression. Acta Materialia, 55, 1607-1616 (2007) |
| [29] | VOLKERT, C. A. and LILLEODDEN, E. T. Size effects in the deformation of sub-micron Au columns. Philosophical Magazine, 86, 5567-5579 (2006) |
| [30] | GREER, J. R. and NIX, W. D. Nanoscale gold pillars strengthened through dislocation starvation. Physical Review B: Condensed Matter and Materials Physics, 73, 245410 (2006) |
| [31] | CUI, Y. N., LIN, P., LIU, Z. L., and ZHUANG, Z. Theoretical and numerical investigations of single arm dislocation source controlled plastic flow in FCC micropillars. International Journal of Plasticity, 55, 279-292 (2014) |
| [32] | PARTHASARATHY, T. A., RAO, S. I., DIMIDUK, D. M., UCHIC, M. D., and TRINKLE, D. R. Contribution to size effect of yield strength from the stochastics of dislocation source lengths in finite samples. Scripta Materialia, 56, 313-316 (2007) |
| [33] | RAO, S. I., DIMIDUK, D. M., TANG, M., UCHIC, M. D., PARTHASARATHY, T. A., and WOODWARD, C. Estimating the strength of single-ended dislocation sources in micron-sized single crystals. Philosophical Magazine, 87, 4777-4794 (2007) |
| [34] | LIEBIG, J. P., KRAU, S., GÖKEN, M., and MERLE, B. Influence of stacking fault energy and dislocation character on slip transfer at coherent twin boundaries studied by micropillar compression. Acta Materialia, 154, 261-272 (2018) |
| [35] | CUI, Y. N., PO, G., and GHONIEM, N. Temperature insensitivity of the flow stress in body-centered cubic micropillar crystals. Acta Materialia, 108, 128-137 (2016) |
| [36] | XIE, D. Y., CHEN, M. J., GIGAX, J., LUSCHER, D., WANG, J., HUNTER, A., FENSIN, S., ZIKRY, M., and LI, N. A fundamental understanding of how dislocation densities affect strain hardening behavior in copper single crystalline micropillars. Mechanics of Materials, 184, 104731 (2023) |
| [37] | MOTZ, C., WEYGAND, D., SENGER, J., and GUMBSCH, P. Initial dislocation structures in 3-D discrete dislocation dynamics and their influence on microscale plasticity. Acta Materialia, 57, 1744-1754 (2009) |
| [38] | HARTMAIER, A., FIVEL, M. C., CANOVA, G. R., and GUMBSCH, P. Image stresses in a free-standing thin film. Modelling and Simulation in Materials Science and Engineering, 7, 781-793 (1999) |
| [39] | MAURISSEN, Y. and CAPELLA, L. Stress field of a dislocation segment perpendicular to a free surface. Philosophical Magazine, 30, 679-683 (1974) |
| [40] | SZAJEWSKI, B. A. and CURTIN, W. A. Analysis of spurious image forces in atomistic simulations of dislocations. Modelling and Simulation in Materials Science and Engineering, 23, 1-17 (2015) |
| [41] | LI, J. C. M. Stress field of a dislocation segment. Philosophical Magazine, 10, 1097-1098 (1964) |
| [42] | ASANO, S. Stress tensor of a finite dislocation. Journal of the Physical Society of Japan, 25, 220-226 (1968) |
| [43] | WILLIS, J. R. Stress fields produced by dislocations in anisotropic media. Philosophical Magazine, 21, 931-949 (1970) |
| [44] | DEVINCRE, B. Three dimensional stress field expressions for straight dislocation segments. Solid State Communications, 93, 875-878 (1995) |
| [45] | DESHPANDE, V. S., NEEDLEMAN, A., and VAN DER GIESSEN, E. Plasticity size effects in tension and compression of single crystals. Journal of the Mechanics and Physics of Solids, 53, 2661-2691 (2005) |
| [46] | HAN, C. S., HARTMAIER, A., GAO, H. J., and HUANG, Y. G. Discrete dislocation dynamics simulations of surface induced size effects in plasticity. Materials Science and Engineering: A, 415, 225-233 (2006) |
| [47] | KONDORI, B., NEEDLEMAN, A., and BENZERGA, A. A. Discrete dislocation simulations of compression of tapered micropillars. Journal of the Mechanics and Physics of Solids, 101, 223-234 (2017) |
| [48] | ZHENG, Z. B., PRASTITI, N. G., BALINT, D. S., and DUNNE, F. P. E. The dislocation configurational energy density in discrete dislocation plasticity. Journal of the Mechanics and Physics of Solids, 129, 39-60 (2019) |
| [49] | YAN, S. H., ZHOU, H. Y., and QIN, Q. H. Microstructure versus size: nano/microscale deformation of solute-strengthening Al alloys via pillar compression tests. Materials Research Letters, 7, 53-59 (2019) |
| [50] | ZHOU, C. Z., BINER, S. B., and LESAR, R. Discrete dislocation dynamics simulations of plasticity at small scales. Acta Materialia, 58, 1565-1577 (2010) |
| [51] | HONDA, K. Dislocation walls consisting of double arrays in white tin single crystals. Japanese Journal of Applied Physics, 18, 215-224 (1979) |
| [52] | LIN, P., LIU, Z. L., CUI, Y. N., and ZHUANG, Z. A stochastic crystal plasticity model with size-dependent and intermittent strain bursts characteristics at micron scale. International Journal of Solids and Structures, 69, 267-276 (2015) |
| [53] | NORFLEET, D. M., DIMIDUK, D. M., POLASIK, S. J., UCHIC, M. D., and MILLS, M. J. Dislocation structures and their relationship to strength in deformed nickel microcrystals. Acta Materialia, 56, 2988-3001 (2008) |
| [54] | TAKEUCHI, S., EDAGAWA, K., and KAMIMURA, Y. Theoretical justification of single-ended dislocation-source-controlled deformation of micropillar FCC crystals. Physical Review Letters, 126, 155501 (2021) |
| [55] | SHAN, Z. W., MISHRA, R. K., ASIF, S. A. S., WARREN, O. L., and MINOR, A. M. Mechanical annealing and source-limited deformation in submicrometre-diameter Ni crystals. Nature Materials, 7, 115-119 (2008) |
| [56] | CUI, Y. N., LIU, Z. L., WANG, Z. J., and ZHUANG, Z. Mechanical annealing under low-amplitude cyclic loading in micropillars. Journal of the Mechanics and Physics of Solids, 89, 1-15 (2016) |
| [57] | GURUPRASAD, P. J. and BENZERGA, A. A. Size effects under homogeneous deformation of single crystals: a discrete dislocation analysis. Journal of the Mechanics and Physics of Solids, 56, 132-156 (2008) |
| [58] | BENZERGA, A. A. Micro-pillar plasticity: 2.5D mesoscopic simulations. Journal of the Mechanics and Physics of Solids, 57, 1459-1469 (2009) |
| [59] | ZHU, Y. C. and XIANG, Y. A continuum model for dislocation dynamics in three dimensions using the dislocation density potential functions and its application to micro-pillars. Journal of the Mechanics and Physics of Solids, 84, 230-253 (2015) |
| [1] | Lu LU, Min LI, Shuang WANG. Surface effects on buckling instability and large deformation of magneto-active soft beams [J]. Applied Mathematics and Mechanics (English Edition), 2025, 46(4): 617-632. |
| [2] | Xin FENG, Liaoliang KE, Yang GAO. Love wave propagation in one-dimensional piezoelectric quasicrystal multilayered nanoplates with surface effects [J]. Applied Mathematics and Mechanics (English Edition), 2024, 45(4): 619-632. |
| [3] | Xiuchen GONG, Yinghao NIE, Gengdong CHENG, Kai LI. Effect of boundary conditions on shakedown analysis of heterogeneous materials [J]. Applied Mathematics and Mechanics (English Edition), 2024, 45(1): 39-68. |
| [4] | Yunzhi HUANG, Wenqing ZHENG, Xiuhua CHEN, Miaolin FENG. Analytic solution of quasicrystal microsphere considering the thermoelectric effect and surface effect in the elastic matrix [J]. Applied Mathematics and Mechanics (English Edition), 2023, 44(8): 1331-1350. |
| [5] | Biao HU, Juan LIU, Yuxing WANG, Bo ZHANG, Jing WANG, Huoming SHEN. Study on wave dispersion characteristics of piezoelectric sandwich nanoplates considering surface effects [J]. Applied Mathematics and Mechanics (English Edition), 2022, 43(9): 1339-1354. |
| [6] | Wenjun WANG, Feng JIN, Tianhu HE, Yongbin MA. Nonlinear magneto-mechanical-thermo coupling characteristic analysis for transport behaviors of carriers in composite multiferroic piezoelectric semiconductor nanoplates with surface effect [J]. Applied Mathematics and Mechanics (English Edition), 2022, 43(9): 1323-1338. |
| [7] | Lele ZHANG, Jing ZHAO, Guoquan NIE, Jinxi LIU. Propagation of Rayleigh-type surface waves in a layered piezoelectric nanostructure with surface effects [J]. Applied Mathematics and Mechanics (English Edition), 2022, 43(3): 327-340. |
| [8] | Ye XIAO, J. SHANG, L. Z. KOU, Chun LI. Surface deformation-dependent mechanical properties of bending nanowires: an ab initio core-shell model [J]. Applied Mathematics and Mechanics (English Edition), 2022, 43(2): 219-232. |
| [9] | Shunzu ZHANG, Qianqian HU, Wenjuan ZHAO. Surface effect on band structure of magneto-elastic phononic crystal nanoplates subject to magnetic and stress loadings [J]. Applied Mathematics and Mechanics (English Edition), 2022, 43(2): 203-218. |
| [10] | Zhina ZHAO, Junhong GUO. Surface effects on a mode-III reinforced nano-elliptical hole embedded in one-dimensional hexagonal piezoelectric quasicrystals [J]. Applied Mathematics and Mechanics (English Edition), 2021, 42(5): 625-640. |
| [11] | Lei ZHANG. Mechanical effects of circular liquid inclusions inside soft matrix: role of internal pressure change and surface tension [J]. Applied Mathematics and Mechanics (English Edition), 2021, 42(4): 501-510. |
| [12] | Baijian WU, Sheng ZHOU, Zhaoxia LI. Analytical solution for the stress field of hierarchical defects: multiscale framework and applications [J]. Applied Mathematics and Mechanics (English Edition), 2021, 42(2): 183-208. |
| [13] | Xu WANG, Ping YANG, P. SCHIAVONE. A screw dislocation near one open inhomogeneity and another closed inhomogeneity both permitting constant interior stresses [J]. Applied Mathematics and Mechanics (English Edition), 2021, 42(2): 173-182. |
| [14] | Siyu WANG, Lin ZHAN, Huifeng XI, O. T. BRUHNS, Heng XIAO. Unified simulation of hardening and softening effects for metals up to failure [J]. Applied Mathematics and Mechanics (English Edition), 2021, 42(12): 1685-1702. |
| [15] | Lianhe LI, Xiaowei CUI, Junhong GUO. Interaction between a screw dislocation and an elliptical hole with two asymmetrical cracks in a one-dimensional hexagonal quasicrystal with piezoelectric effect [J]. Applied Mathematics and Mechanics (English Edition), 2020, 41(6): 899-908. |
| Viewed | ||||||
|
Full text |
|
|||||
|
Abstract |
|
|||||
