Fig. 1

The design concept of TLPL based on TPMS lattice: (a) the P-type TPMS lattice and the resulting TLPL; (b) design method of the TLPL; (c) TLPL from P-type TPMS with its one-eighth defined by four generative parameters including a, b, h, and l (color online)"

Fig. 2

(a) The P-type, D-type, and I-WP TPMS lattices and the corresponding novel TLPLs; (b) a series of TLPLs with different generative parameters from a given type of TPMS with a fixed relative density of 0.6 (color online)"

Fig. 3

Design space of the P-type TLPL: (a) two bound surfaces; (b) the lower and upper bounds of h/L corresponding to the available combinations of a/L and b/L; (c) a set of TLPLs with generative parameters uniformly distributed in the design space and five groups of typical configurations of the P-type TLPL with the specially selected Ξ; (d) designed domain for the relative density ρ* with the generative parameters a/L and b/L; (e) the lower and upper bounds of the relative density ρ* for the given ranges of a/L and b/L (color online)"

Fig. 4

(a) The architecture of the ANN model; (b) the demonstration of its prediction accuracy (color online)"

Fig. 5

The flowchart of the proposed ANN-based genetic algorithm"

Fig. 6

(a) Nine TLPL specimens fabricated by SLM with their labels; (b) the universal material testing machine INSTRON 5985 utilized for the mechanical testing (color online)"

Table 1

Information of nine TLPL structure specimens"

Fig. 7

The effective mechanical properties of TLPLs with different generative parameters while keeping the relative density constant: (a), (b), and (c) for the relative density of 0.1; (d), (e), and (f) for the relative density of 0.2, where the normalized specific elastic modulus, normalized specific shear modulus, and anisotropic index are presented in sequence (color online)"

Fig. 8

The effective mechanical properties of TLPLs and other lattices: (a) the normalized specific elastic modulus; (b) the normalized specific shear modulus; (c) the anisotropic index of TLPLs with different generative parameters, where six representative TLPLs with extreme anisotropic indices are presented in (c); (d), (e), and (f) show variations of these mechanical properties with respect to the relative density for five types of lattices as presented in (g), including TLPL, TPMS, TLPL-u, SCH, and OCT (color online)"

Fig. 9

Normalized specific yield strengths of TLPLs with (a) different combinations of a/L and b/L at a relative density of 0.2, (b) different combinations of a/L, b/L, and h/L, and (c) different relative densities (color online)"

Fig. 10

Optimized TLPLs at relative densities of 0.05, 0.2, and 0.5 with the maximum of (a) normalized specific elastic modulus and (b) the normalized specific shear modulus, where the final configurations are provided on the right-hand side of each subfigure, and the effective mechanical properties from the FE model for both the optimized TLPLs and TPMS are presented for comparison (color online)"

Table 2

Optimization results of non-isotropic TLPLs at different relative densities"

Table 3

Optimization results of isotropic TLPLs for different relative densities"

Fig. 11

Optimized isotropic TLPLs at different relative densities: (a) configurations with the maximum of elastic modulus or yield strength using the proposed ANN-based optimization method, and the comparison of (b) the maximum of normalized specific shear modulus and (c) the maximum of normalized specific yield strength among different optimization methods and TLPLs, where ANN denotes the results from the ANN-based optimization method, response surface method (RSM) denotes the results from the genetic algorithm with the RSM for fitness estimation, "P" and "E" denote the optimized TLPLs using the proposed method with the maximum of effective specific yield strength and effective specific elastic modulus, respectively, the subscript "prediction" indicates the result from the optimization method, and the subscript "simulation" indicates the result from the FE model for the optimized TLPL (color online)"

Fig. 12

Comparison of normalized specific elastic modulus with respect to the relative density among four different types of isotropic lattices, where ITL is short for isotropic truss lattice[19], B-BCC is short for bamboo-inspired BCC lattice[24], and SC is short for the simple-cubic shell lattice[18] (color online)"

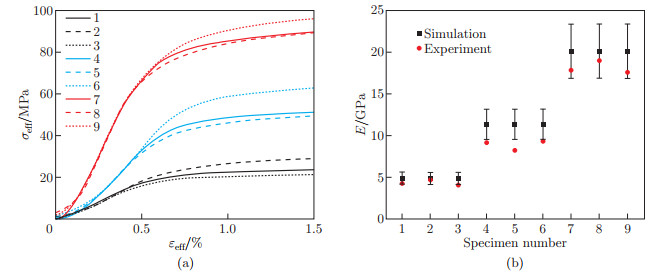
Fig. 13

Experimental data and numerical results for the nine isotropic TLPL structure specimens: (a) effective stress-strain curves from the compression experiments; (b) comparison of effective elastic modulus between experimental data and numerical results from the FE model, where error bars of the numerical results are obtained by taking the maximum and minimum elastic moduli of the base material fabricated by SLM as inputs (color online)"