Applied Mathematics and Mechanics (English Edition) ›› 2025, Vol. 46 ›› Issue (10): 1967-1982.doi: https://doi.org/10.1007/s10483-025-3307-6
Previous Articles Next Articles
Qiaoyun ZHANG1,2,†( ), Xiaoyan ZHANG1, Jiahao XU1, Zhicai SONG1, Minghao ZHAO1,2,3
), Xiaoyan ZHANG1, Jiahao XU1, Zhicai SONG1, Minghao ZHAO1,2,3
Received:2025-05-23
Revised:2025-08-11
Published:2025-09-30
Contact:
Qiaoyun ZHANG, E-mail: zhangqy@zzu.edu.cnSupported by:2010 MSC Number:
Qiaoyun ZHANG, Xiaoyan ZHANG, Jiahao XU, Zhicai SONG, Minghao ZHAO. Vibration characteristic analysis of a cracked piezoelectric semiconductor curved beam. Applied Mathematics and Mechanics (English Edition), 2025, 46(10): 1967-1982.
Table 1
Material constants of ZnO[42]"
| Property | Parameter | Value | Unit |
|---|---|---|---|
| Elastic constant | 209.7 | GPa | |
| 121.1 | GPa | ||
| 105.1 | GPa | ||
| 210.9 | GPa | ||
| 42.47 | GPa | ||
| Piezoelectric constant | C·m-2 | ||
| C·m-2 | |||
| 1.32 | C·m-2 | ||
| Dielectric constant | C·V-1·m-1 | ||
| C·V-1·m-1 | |||
| Electron mobility | 0.02 | m2·V-1·s-1 | |
| 0.02 | m2·V-1·s-1 | ||
| Diffusion constant | m2·s-1 | ||
| m2·s-1 | |||
| Mass density | 5 680 | kg·m-3 |
Fig. 5
Distributions of the electromechanical field along the θ-direction: (a) real part of the extensional displacement W; (b) imaginary part of the extensional displacement W; (c) imaginary part of the circumferential displacement uθ; (d) imaginary part of the radial displacement ur; (e) imaginary part of the potential Φ; (f) imaginary part of the electron concentration perturbation N (color online)"
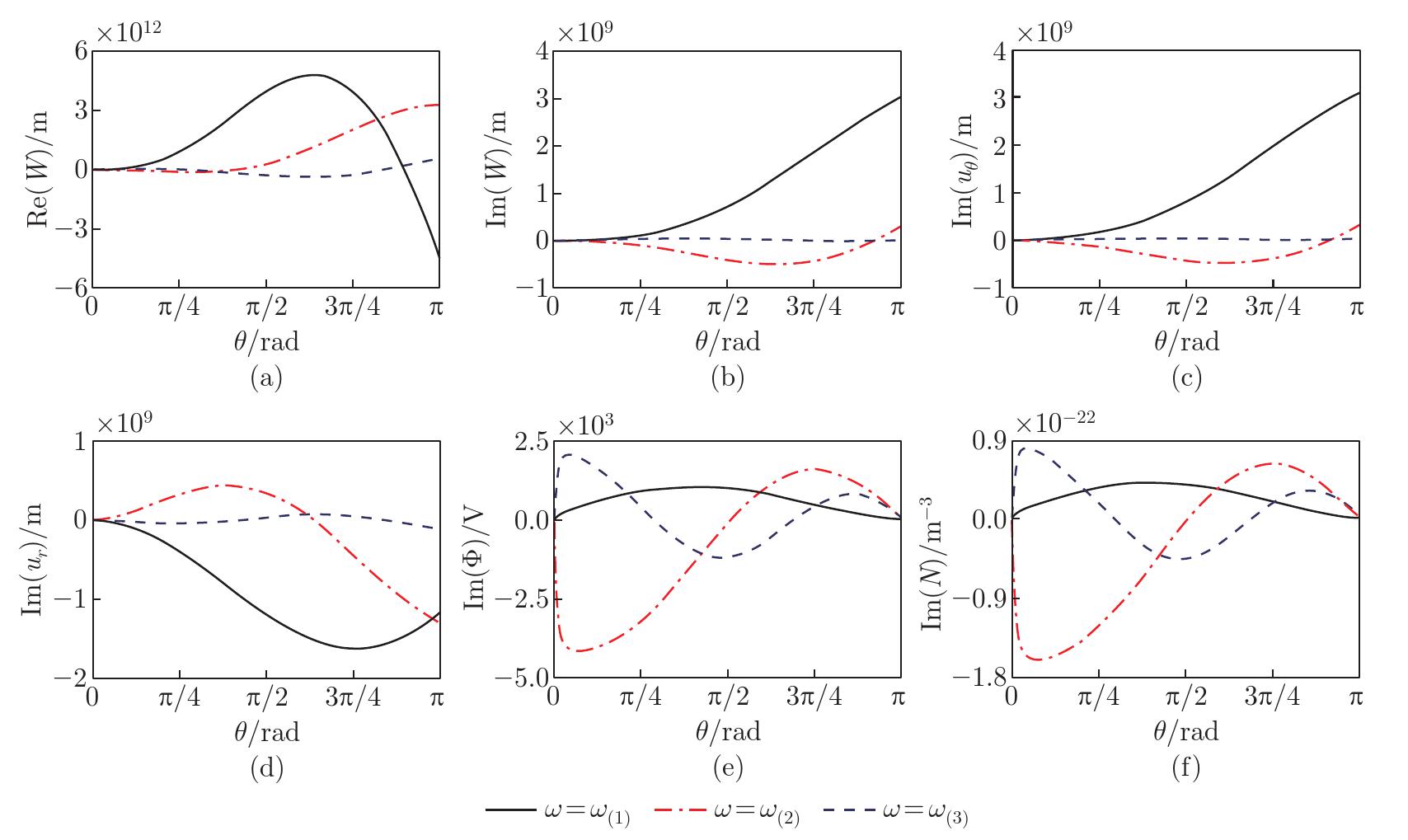
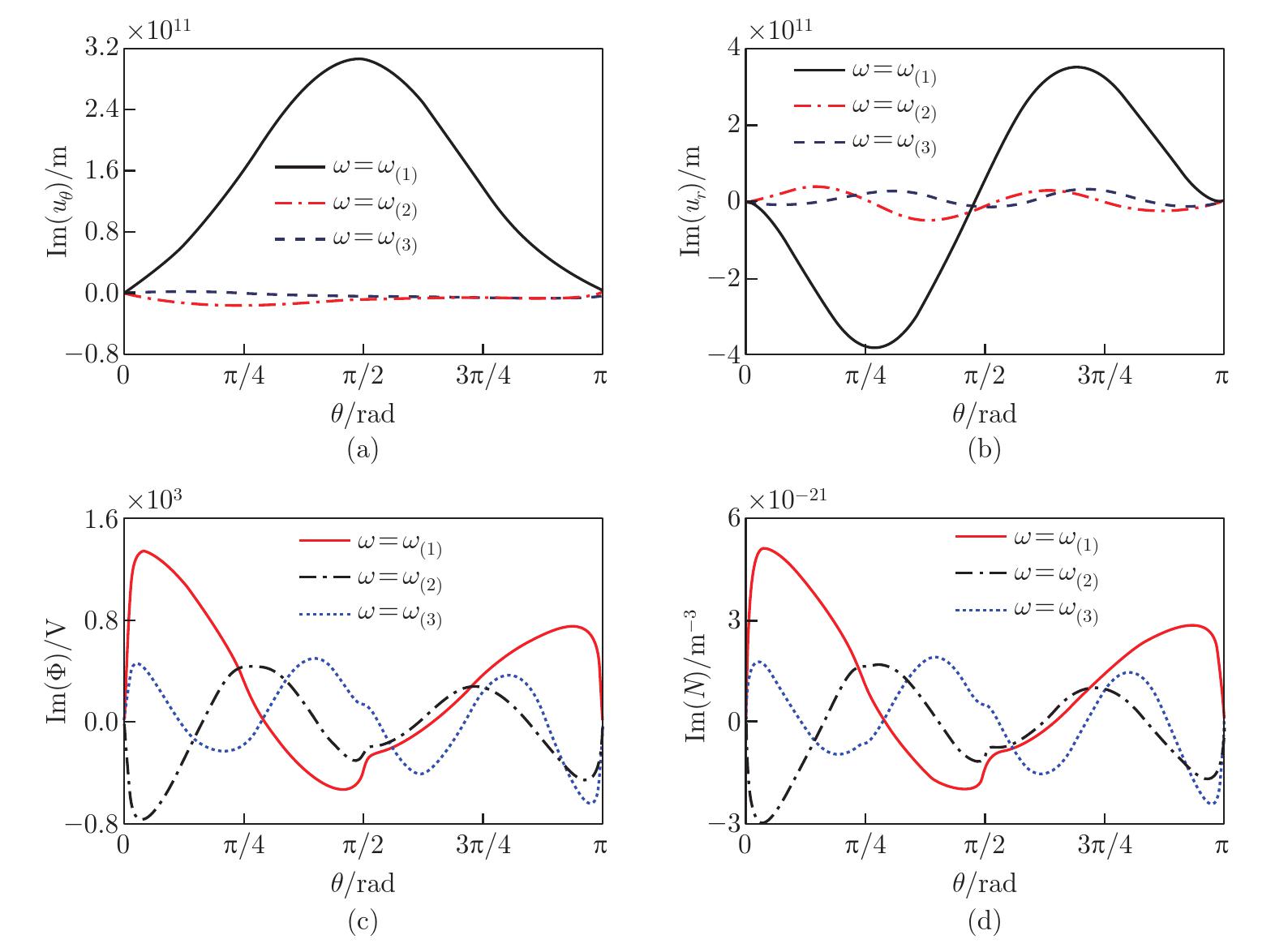
Fig. 7
Electromechanical field distributions along the θ-direction for a cracked ZnO curved beam: (a) imaginary part of the circumferential displacement uθ; (b) imaginary part of the radial displacement ur; (c) imaginary component of the potential Φ; (d) imaginary component of the electron concentration perturbation N (color online)"
| [1] | WANG, X. D., ZHOU, J., SONG, J. H., JIN, L., XU, N. S., and WANG, Z. L. Piezoelectric field effect transistor and nanoforce sensor based on a single ZnO nanowire. Nano Letters, 6(12), 2768–2772 (2006) |
| [2] | SHIM, Y. S., ZHANG, L., KIM, D. H., YOU, R. C., NAHM, S. H., KANG, C. Y., LEE, W., and JANG, H. W. Highly sensitive and selective H2 and NO2 gas sensors based on surface-decorated WO3 nanoigloos. Sensors and Actuators B-Chemical, 198(2), 294–301 (2014) |
| [3] | PU, X. G., SONG, J., JIN, L., and WANG, Z. L. Nanowire piezoelectric nanogenerators on plastic substrates as flexible power sources for nanodevices. Advanced Materials, 19(1), 67–72 (2006) |
| [4] | PURUSOTHAMAN, Y., ALLURI, N. R., CHANDRASEKHAR, A., and KIM, S. J. Photoactive piezoelectric energy harvester driven by antimony sulfoiodide (SbSI): a AV BVI CVII class ferroelectric-semiconductor compound. Nano Energy, 50, 256–265 (2018) |
| [5] | DIETZ, D. R. and BUSSE, L. J. Acoustoelectric detection of ultrasound power with composite piezoelectric and semiconductor devices. IEEE Transactions on Ultrasonics Ferroelectrics and Frequency Control, 35(2), 146–151 (1988) |
| [6] | KINO, G. S. Acoustoelectric interactions in acoustic-surface-wave devices. Proceedings of the IEEE, 64(5), 724–748 (1976) |
| [7] | YANG, Q., WANG, W. H., XU, S., and WANG, Z. L. Enhancing light emission of ZnO microwire-based diodes by piezo-phototronic effect. Nano Letters, 11(9), 4012–4017 (2011) |
| [8] | WANG, Z. L. Nanopiezotronics. Advanced Materials, 19(6), 889–892 (2007) |
| [9] | WANG, Z. L. Piezopotential gated nanowire devices: piezotronics and piezo-phototronics. Nano Today, 5(6), 540–552 (2010) |
| [10] | ZHANG, C. L., WANG, X. Y., CHEN, W. Q., and YANG, J. S. An analysis of the extension of a ZnO piezoelectric semiconductor nanofiber under an axial force. Smart Materials and Structures, 26(2), 025030 (2017) |
| [11] | YANG, G. Y., DU, J. K., WANG, J., and YANG, J. S. Extension of a piezoelectric semiconductor fiber with consideration of electrical nonlinearity. Acta Mechanica, 229(11), 4663–4676 (2018) |
| [12] | CHENG, R. R., ZHANG, C., CHEN, W. Q., and YANG, J. S. Piezotronic effects in the extension of a composite fiber of piezoelectric dielectrics and nonpiezoelectric semiconductors. Journal of Applied Physics, 124(6), 064506 (2018) |
| [13] | LI, P., JIN, F., and MA, J. X. One-dimensional dynamic equations of a piezoelectric semiconductor beam with a rectangular cross section and their application in static and dynamic characteristic analysis. Applied Mathematics and Mechanics (English Edition), 39(5), 685–702 (2018) https://doi.org/10.1007/s10483-018-2325-6 |
| [14] | HAN, C. F., LU, C. S., ZHAO, M. H., and ZHANG, Q. Y. Nonlinear finite element analysis of electromechanical behaviors in a piezoelectric semiconductor beam. International Journal of Non-linear Mechanics, 49, 104311 (2023) |
| [15] | LIU, Z. W., BIAN, P. L., QU, Y. L., HUANG, W. C., CHEN, L. L., CHEN, J. B., SAXENA, P., and YU, T. T. A Galerkin approach for analysing coupling effects in the piezoelectric semiconducting beams. European Journal of Mechanics-A/Solids, 103, 105145 (2024) |
| [16] | WANG, G. L., LIU, J. X., LIU, X. L., FENG, W. J., and YANG, J. S. Extensional vibration characteristics and screening of polarization charges in a ZnO piezoelectric semiconductor nanofiber. Journal of Applied Physics, 124(9), 094502 (2018) |
| [17] | DAI, X. Y., ZHU, F., QIAN, Z. H., and YANG, J. S. Electric potential and carrier distribution in a piezoelectric semiconductor nanowire in time-harmonic bending vibration. Nano Energy, 43, 22–28 (2018) |
| [18] | YAN, Y. X., ZHU, C. S., and FANG, X. Q. Free vibration of three-layered piezoelectric semiconductor rectangular beam. Materials Today Communications, 38, 107859 (2024) |
| [19] | QU, Y. L., JIN, F., and YANG, J. S. Stress-induced electric potential barriers in thickness-stretch deformations of a piezoelectric semiconductor plate. Acta Mechanica, 232(11), 4533–4543 (2021) |
| [20] | LI, M. E., ZHANG, Q. Y., WANG, B. B., and ZHAO, M. H. Analysis of flexural vibrations of a piezoelectric semiconductor nanoplate driven by a time-harmonic force. Materials, 14(14), 3926 (2021) |
| [21] | REN, C., WANG, K. F., and WANG, B. L. Adjusting the electromechanical coupling behaviors of piezoelectric semiconductor nanowires via strain gradient and flexoelectric effects. Journal of Applied Physics, 128(21), 215701 (2020) |
| [22] | CHU, L. L., DUI, G., MEI, H., LIU, L. S., and LI, Y. B. An analysis of flexoelectric coupling associated electroelastic fields in functionally graded semiconductor nanobeams. Journal of Applied Physics, 130(11), 115701 (2021) |
| [23] | SLADEK, J., SLADEK, V., REPKA, M., and PAN, E. Size effect in piezoelectric semiconductor nanostructures. Journal of Intelligent Material Systems and Structures, 33(11), 1351–1363 (2022) |
| [24] | YANG, J. S. An anti-plane crack in a piezoelectric semiconductor. International Journal of Fracture, 136, L27–L32 (2005) |
| [25] | HU, Y. T., ZENG, Y., and YANG, J. S. A mode III crack in a piezoelectric semiconductor of crystals with 6mm symmetry. International Journal of Solids and Structures, 44(11-12), 3928–3938 (2007) |
| [26] | SLADEK, J., SLADEK, V., PAN, E., and WÜNSCHE, M. Fracture analysis in piezoelectric semiconductors under a thermal load. Engineering Fracture Mechanics, 126, 27–39 (2014) |
| [27] | FAN, C. Y., YAN, Y., XU, G. T., and ZHAO, M. H. Piezoelectric-conductor iterative method for analysis of cracks in piezoelectric semiconductors via the finite element method. Engineering Fracture Mechanics, 165, 183–196 (2016) |
| [28] | ZHANG, Q. Y., FAN, C. Y., XU, G. T., and ZHAO, M. H. Iterative boundary element method for crack analysis of two-dimensional piezoelectric semiconductor. Engineering Analysis with Boundary Elements, 83, 87–95 (2017) |
| [29] | ZHAO, M. H., PAN, Y. B., FAN, C. Y., and XU, G. T. Extended displacement discontinuity method for analysis of cracks in 2D piezoelectric semiconductors. International Journal of Solids and Structures, 94-95, 50–59 (2016) |
| [30] | ZHAO, Y. F., ZHOU, C. G., ZHAO, M. H., PAN, E., and FAN, C. Y. Penny-shaped cracks in three-dimensional piezoelectric semiconductors via Green’s functions of extended displacement discontinuity. Journal of Intelligent Material Systems and Structures, 28(13), 1775–1788 (2017) |
| [31] | QIN, G. S., MA, S. J., LU, C., WANG, G., and ZHAO, M. H. Influence of electric field and current on the strength of depoled GaN piezoelectric semiconductive ceramics. Ceramics International, 44, 4169–4175 (2018) |
| [32] | PAPADOPOULOS, C. A. and DIMAROGONAS, A. D. Coupled longitudinal and bending vibration of a rotating shaft with an open crack. Journal of Sound and Vibration, 117(1), 81–93 (1987) |
| [33] | GOUNARIS, G. and DIMAROGONAS, A. A finite element of a cracked prismatic beam for structural analysis. Computers & Structures, 28(3), 309–313 (1988) |
| [34] | ARIA, A. I., FRISWELL, M. I., and RABCZUK, T. Thermal vibration analysis of cracked nanobeams embedded in an elastic matrix using finite element analysis. Composite Structures, 212, 118–128 (2019) |
| [35] | ZHU, X., LI, T. Y., ZHAO, Y., and LIU, J. X. Structural power flow analysis of Timoshenko beam with an open crack. Journal of Sound and Vibration, 297, 215–226 (2006) |
| [36] | MAO, J. J., WANG, Y. J., ZHANG, W., WU, M. Q., LIU, Y. Z., and LIU, X. H. Vibration and wave propagation in functionally graded beams with inclined cracks. Applied Mathematical Modelling, 118, 166–184 (2023) |
| [37] | KUANG, Y. D., LI, G. Q., and CHEN, C. Y. Admittance function of active piezoelectric elements bonded on a curved cracked beam. Journal of Intelligent Material Systems and Structures, 19(2), 181–191 (2008) |
| [38] | KUANG, Y. D., LI, G. Q., and CHEN, C. Y. An admittance function of active piezoelectric elements bonded on a cracked beam. Journal of Sound and Vibration, 298, 393–403 (2006) |
| [39] | ZHANG, Q. Y., XU, J. H., WANG, B. B., ZHAO, M. H., and LU, C. S. Bending characteristics of a one-dimensional piezoelectric semiconductor curved beam. Archive of Applied Mechanics, 94(10), 2807–2818 (2024) |
| [40] | LI, S. R., CAO, D. F., and WAN, Z. Q. Bending solutions of FGM Timoshenko beams from those of the homogenous Euler-Bernoulli beams. Applied Mathematical Modelling, 37(10-11), 7077–7085 (2013) |
| [41] | XIONG, Y. P., XING, J. T., and PRICE, W. G. Interactive power flow characteristics of an integrated equipment-nonlinear isolator-travelling flexible ship excited by sea waves. Journal of Sound and Vibration, 287(1), 245–276 (2005) |
| [42] | LI, D. Z., ZHANG, C. L., ZHANG, S., WANG, H. M., CHEN, W. Q., and ZHANG, C. Z. Propagation of terahertz elastic longitudinal waves in piezoelectric semiconductor rods. Ultrasonics, 132, 106964 (2023) |
| [43] | RYU, C. H., HWAN, W., CHO, J. Y., KIM, S. B., KIM, K. B., SONG, Y., and SUNG, T. H. Optimization of the energy conversion efficiency by bending deflection of piezoelectric cantilever beams. Journal of the Korea Physical Society, 76(10), 948–953 (2020) |
| [1] | Ru TIAN, Lisha YI, Guoquan NIE, Jinxi LIU, Ernian PAN, Yuesheng WANG. Lamb waves in multilayered piezoelectric semiconductor plates [J]. Applied Mathematics and Mechanics (English Edition), 2025, 46(8): 1493-1510. |
| [2] | Dejuan KONG, Zhuangzhuang HE, Chengbin LIU, Chunli ZHANG. Analysis of multi-field coupling behaviors of sandwich piezoelectric semiconductor beams under thermal loadings [J]. Applied Mathematics and Mechanics (English Edition), 2025, 46(8): 1571-1590. |
| [3] | Zeyu CHAI, Zhen ZHANG, Kefan XU, Xuyuan SONG, Yewei ZHANG, Liqun CHEN. An innovative nonlinear bionic X-shaped vibration isolator enhanced by quasi-zero stiffness characteristics: theory and experimental investigation [J]. Applied Mathematics and Mechanics (English Edition), 2025, 46(8): 1475-1492. |
| [4] | N. A. SAEED, Y. Y. ELLABBAN, Lei HOU, Haiming YI, Shun ZHONG, F. Z. DURAIHEM, O. M. OMARA. Nonlinear vibration of quasi-zero stiffness structure with piezoelectric harvester and RL-load: intra-well and inter-well oscillation modes under 1:1 internal resonance [J]. Applied Mathematics and Mechanics (English Edition), 2025, 46(8): 1451-1474. |
| [5] | Shun WENG, Liying WU, Zuoqiang LI, Lanbin ZHANG, Huliang DAI. Optimizing wind energy harvester with machine learning [J]. Applied Mathematics and Mechanics (English Edition), 2025, 46(8): 1417-1432. |
| [6] | Lele ZHANG, Zheng ZHAO, Xiaofan HU, Guoquan NIE, Jinxi LIU. Exact multi-field coupling modeling and analysis of piezoelectric semiconductor plates [J]. Applied Mathematics and Mechanics (English Edition), 2025, 46(7): 1331-1346. |
| [7] | Weixing ZHANG, Dongshuo YANG, Xiangying GUO. Low-frequency vibration suppression of meta-beam withsoftening nonlinearity [J]. Applied Mathematics and Mechanics (English Edition), 2025, 46(6): 1011-1028. |
| [8] | Jie JING, Xiaoye MAO, Hu DING, Honggang LI, Liqun CHEN. Modeling and mechanism of vibration reduction of pipes by visco-hyperelastic materials [J]. Applied Mathematics and Mechanics (English Edition), 2025, 46(6): 1029-1048. |
| [9] | Chunhao ZHANG, Qingdong CHAI, Changyuan YU, Wuce XING, Yanqing WANG. Theoretical and experimental investigation on vibration of bolted-flange-joined conical-cylindrical shells [J]. Applied Mathematics and Mechanics (English Edition), 2025, 46(6): 1049-1068. |
| [10] | Linyao WANG, Aibing ZHANG, Chuanzeng ZHANG, Jianke DU, Z. M. XIAO, Jia LOU. Rayleigh wave propagation in an elastic half-space with an attached piezoelectric semiconductor layer considering flexoelectricity and size-effects [J]. Applied Mathematics and Mechanics (English Edition), 2025, 46(6): 1069-1088. |
| [11] | Jinming FAN, Zhongbiao PU, Jie YANG, Xueping CHANG, Yinghui LI. Orthogonality conditions and analytical response solutions of damped gyroscopic double-beam system: an example of pipe-in-pipe system [J]. Applied Mathematics and Mechanics (English Edition), 2025, 46(5): 927-946. |
| [12] | Peiliang ZHANG, Jianfei WANG. Macro fiber composite-based active control of nonlinear forced vibration of functionally graded plate [J]. Applied Mathematics and Mechanics (English Edition), 2025, 46(5): 869-884. |
| [13] | Hui MA, Hong GUAN, Lin QU, Xumin GUO, Qinqin MU, Yao ZENG, Yanyan CHEN. Dynamic modeling and simulation of blade-casing system with rubbing considering time-varying stiffness and mass of casing [J]. Applied Mathematics and Mechanics (English Edition), 2025, 46(5): 849-868. |
| [14] | Yueting ZHOU, Qinghui LUO, Lihua WANG, Shenghu DING. Competition between electro-magnetic enhancing and shear stress weakening effects on adhesion behaviors of multiferroic composites [J]. Applied Mathematics and Mechanics (English Edition), 2025, 46(5): 831-848. |
| [15] | Zibo WEI, Peijun WEI, Chunyu XU, Xiao GUO. Dispersion, attenuation, and bandgap of in-plane coupled Bloch waves in piezoelectric semiconductor phononic crystal with PN junction [J]. Applied Mathematics and Mechanics (English Edition), 2025, 46(5): 813-830. |
| Viewed | ||||||
|
Full text |
|
|||||
|
Abstract |
|
|||||


 Email Alert
Email Alert RSS
RSS