Applied Mathematics and Mechanics (English Edition) ›› 2025, Vol. 46 ›› Issue (6): 1069-1088.doi: https://doi.org/10.1007/s10483-025-3265-8
Previous Articles Next Articles
Linyao WANG1, Aibing ZHANG1, Chuanzeng ZHANG2, Jianke DU1, Z. M. XIAO3, Jia LOU1,3,†(
)
Email Alert
RSSReceived:2025-03-24
Revised:2025-04-27
Published:2025-06-06
Contact:
Jia LOU, E-mail: jiajia_smile@163.comSupported by:2010 MSC Number:
Linyao WANG, Aibing ZHANG, Chuanzeng ZHANG, Jianke DU, Z. M. XIAO, Jia LOU. Rayleigh wave propagation in an elastic half-space with an attached piezoelectric semiconductor layer considering flexoelectricity and size-effects. Applied Mathematics and Mechanics (English Edition), 2025, 46(6): 1069-1088.
Fig. 1
Schematic representation of the configuration featuring a PSC layer on an elastic substrate (color online)"
Fig. 2
Comparison of the classical Rayleigh wave dispersion curves obtained by the present model with those by Tian et al.[52]: (a) real component of the phase velocity; (b) imaginary component of the phase velocity (color online)"
Fig. 3
Dispersion and attenuation characteristics with varied flexoelectric coefficients (l¯0=0.15, l¯1=0.3, l¯2=0.15, p0=1×1022 m-3, δ¯=1, α=0, and β=0): (a) dispersion; (b) real component of the phase velocity; (c) imaginary component of the phase velocity (color online)"
Fig. 4
Dispersion and attenuation characteristics with varied micro-inertia characteristic lengths (f¯=0.6, l¯1=0.3, l¯2=0.15, p0=1×1022 m−3, δ¯=1, α=0, and β=0): (a) dispersion; (b) real component of the phase velocity; (c) imaginary component of the phase velocity (color online)"
Fig. 5
Dispersion and attenuation characteristics with varied strain gradient characteristic lengths (f¯=0.6, l¯0=0.15, l¯2=0.15, p0=1×1022 m-3, δ¯=1, α=0, and β=0): (a) dispersion; (b) real component of the phase velocity; (c) imaginary component of the phase velocity (color online)"
Fig. 6
Dispersion and attenuation characteristics with varied electric field gradient characteristic lengths (f¯=0.6, l¯0=0.15, l¯1=0.3, p0=1×1022 m−3, δ¯=1, α=0, and β=0): (a) dispersion; (b) real component of the phase velocity; (c) imaginary component of the phase velocity (color online)"
Fig. 7
Dispersion and attenuation characteristics with varied PSC layer thicknesses (f¯=0.6, l¯0=0.15, l¯1=0.3, l¯2=0.15, p0=1×1022 m−3, α=0, and β=0): (a) dispersion; (b) real component of the phase velocity; (c) imaginary component of the phase velocity (color online)"
Fig. 8
Dispersion and attenuation characteristics with varied steady-state carrier concentrations (f¯=0.6, l¯0=0.15, l¯1=0.3, l¯2=0.15, δ¯=1, α=0, and β=0): (a) dispersion; (b) real component of the phase velocity; (c) imaginary component of the phase velocity (color online)"
Fig. 9
Dispersion and attenuation characteristics with varied bias electric field intensities in the x1-direction (f¯=0.6, l¯0=0.15, l¯1=0.3, l¯2=0.15, p0=1×1022 m−3, δ¯=1, and β=0): (a) dispersion; (b) real component of the phase velocity; (c) imaginary component of the phase velocity (color online)"
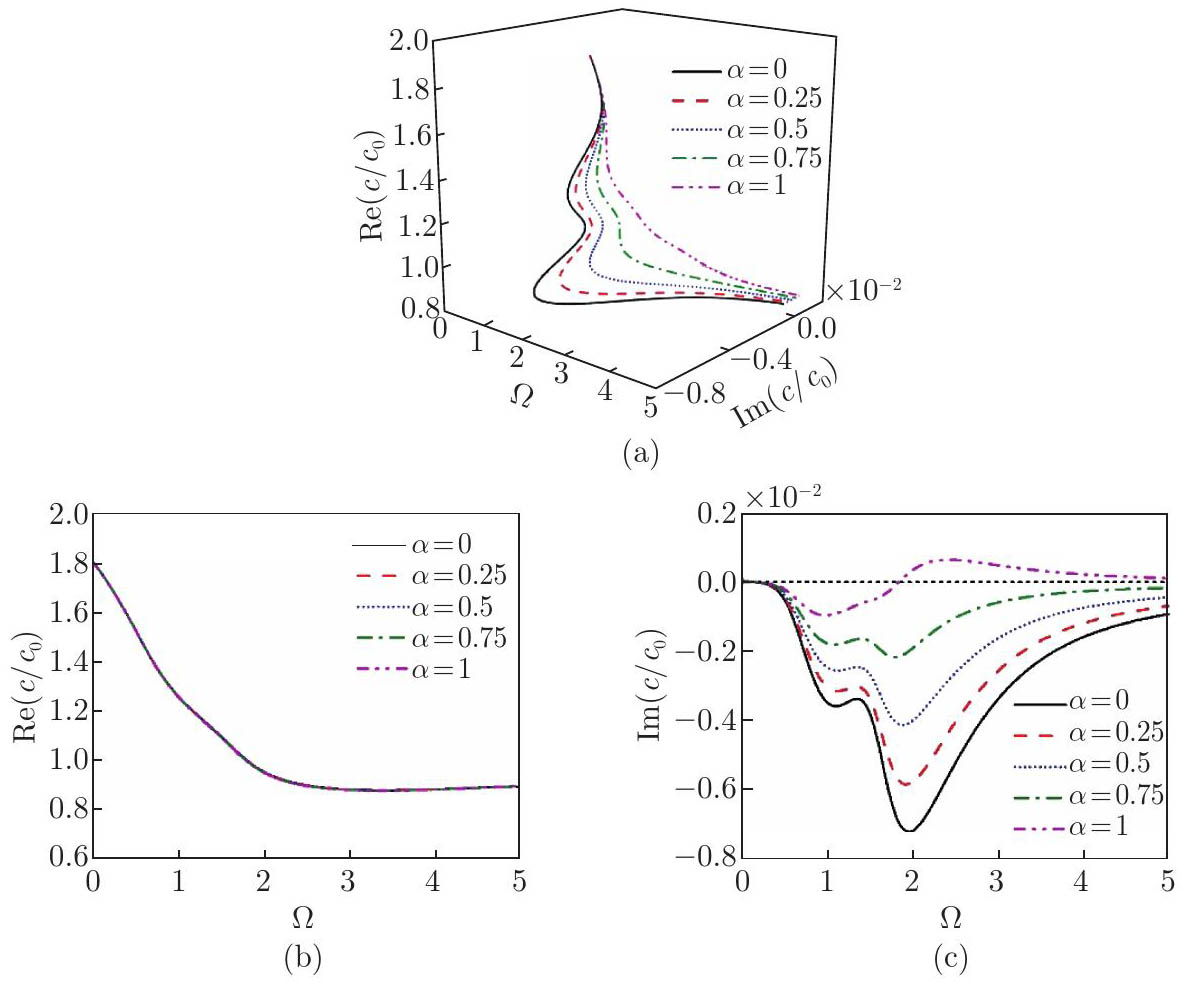
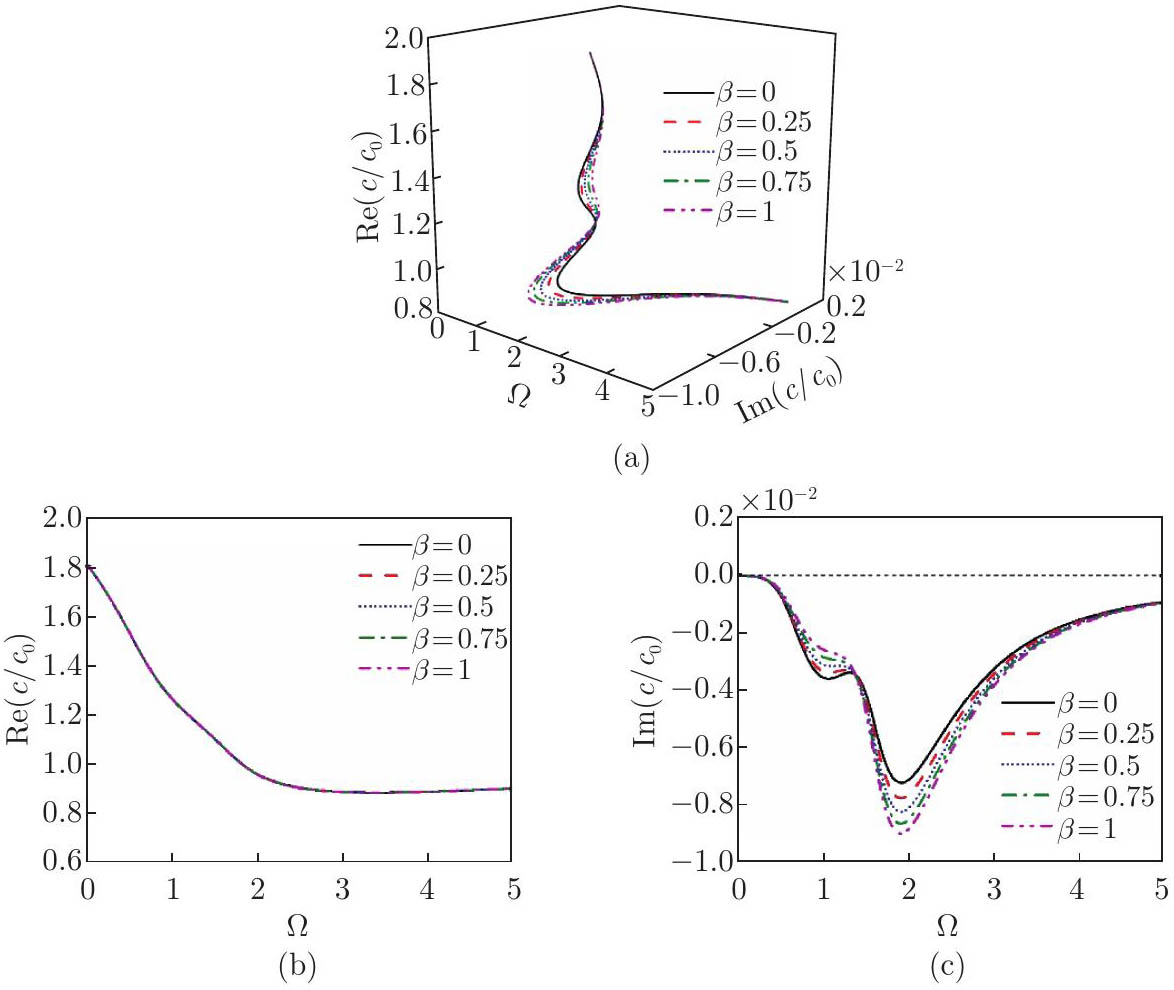
Fig. 10
Dispersion and attenuation characteristics with varied bias electric field intensities in the x3-direction (f¯=0.6, l¯0=0.15, l¯1=0.3, l¯2=0.15, p0=1×1022 m−3, δ¯=1, and α=0): (a) dispersion; (b) real component of the phase velocity; (c) imaginary component of the phase velocity (color online)"
| [1] | WHITE, R. M. and VOLTMER, F. W. Direct piezoelectric coupling to surface elastic waves. Applied Physics Letters, 7(12), 314-316 (1965) |
| [2] | CAO, X. S., HU, S. M., LIU, J. J., and SHI, J. P. Generalized Rayleigh surface waves in a piezoelectric semiconductor half space. Meccanica, 54, 271-281 (2019) |
| [3] | XU, C. Y., WEI, P. J., WEI, Z. B., and GUO, X. Rayleigh wave in layered piezoelectric semiconductor with consideration of PN junction effects. Mathematics and Mechanics of Solids, 28(8), 1817-1833 (2023) |
| [4] | SU, R. X., FU, S. L., SHEN, J. Y., CHEN, Z. L., LU, Z. T., YANG, M. L., WANG, R., ZENG, F., WANG, W. B., and SONG, C. Enhanced performance of ZnO/SiO2/Al2O3 surface acoustic wave devices with embedded electrodes. ACS Applied Materials & Interfaces, 12(37), 42378-42385 (2020) |
| [5] | LEWIS, M. F. Rayleigh waves — a progress report. European Journal of Physics, 16(1), 1-7 (1995) |
| [6] | LAMANNA, L., RIZZI, F., BIANCO, M., AGOSTINI, M., CECCHINI, M., DE VITTORIO, M., and BHETHANABOTLA, V. R. Photoresponse of the AlN-based SAW device on polymeric and silicon substrates. IEEE Sensors Journal, 21(8), 9675-9681 (2021) |
| [7] | HUANG, Y. Q., DAS, P. K., and BHETHANABOTLA, V. R. Surface acoustic waves in biosensing applications. Sensors and Actuators Reports, 3, 100041 (2021) |
| [8] | ZHANG, Y., CAI, Y., ZHOU, J., XIE, Y., XU, Q. W., ZOU, Y., GUO, S. S., XU, H. X., SUN, C. L., and LIU, S. Surface acoustic wave-based ultraviolet photodetectors: a review. Science Bulletin, 65(7), 587-600 (2020) |
| [9] | TAKAGAKI, Y., SANTOS, P., WIEBICKE, E., BRANDT, O., SCHÖNHERR, H. P., and PLOOG, K. Superhigh-frequency surface-acoustic-wave transducers using AlN layers grown on SiC substrates. Applied Physics Letters, 81(14), 2538-2540 (2002) |
| [10] | BÜYÜKKÖSE, S., VRATZOV, B., ATAÇ, D., VAN DER VEEN, J., SANTOS, P., and VAN DER WIEL, W. Ultrahigh-frequency surface acoustic wave transducers on ZnO/SiO2/Si using nanoimprint lithography. Nanotechnology, 23(31), 315303 (2012) |
| [11] | NORDIN, A. N. and ZAGHLOUL, M. E. Modeling and fabrication of CMOS surface acoustic wave resonators. IEEE Transactions on Microwave Theory and Techniques, 55(5), 992-1001 (2007) |
| [12] | JIN, H., ZHOU, J., HE, X. L., WANG, W. B., GUO, H. W., DONG, S. R., WANG, D. M., XU, Y., GENG, J. F., LUO, J., and MILNE, W. I. Flexible surface acoustic wave resonators built on disposable plastic film for electronics and lab-on-a-chip applications. Scientific Reports, 3(1), 2140 (2013) |
| [13] | PETRONI, S., TRIPOLI, G., COMBI, C., VIGNA, B., DE VITTORIO, M., TODARO, M., EPIFANI, G., CINGOLANI, R., and PASSASEO, A. GaN-based surface acoustic wave filters for wireless communications. Superlattices and Microstructures, 36(4-6), 825-831 (2004) |
| [14] | SU, R. X., SHEN, J. Y., LU, Z. T., XU, H. P., NIU, Q. S., XU, Z. B., ZENG, F., SONG, C., WANG, W. B., and FU, S. L. Wideband and low-loss surface acoustic wave filter based on 15° YX-LiNbO3/SiO2/Si structure. IEEE Electron Device Letters, 42(3), 438-441 (2021) |
| [15] | LIU, L. Y., ZHANG, Q. Z., SUN, H., YANG, Y., and ZHAO, X. Y. High order Rayleigh-type SAW devices for advanced 5G front-ends with improved performance. Journal of Physics: Conference Series, 2822, 012173 (2024) |
| [16] | WANG, L. Y., FANG, X., LOU, J., FAN, H., ZHANG, A. B., and DU, J. K. Piezoelectric layer guided in-plane surface waves with flexoelectricity and gradient effects. Engineering Structures, 315, 118483 (2024) |
| [17] | ASSALI, A., LAIDOUDI, F., SERHANE, R., KANOUNI, F., and MEZILET, O. Highly enhanced electro-acoustic properties of YAlN/sapphire based surface acoustic wave devices for next generation of microelectromechanical systems. Materials Today Communications, 26, 102067 (2021) |
| [18] | WU, C. Y., LOU, J., HE, L. W., DU, J. K., and WU, H. P. Buckling and post-buckling of symmetric functionally graded microplate lying on nonlinear elastic foundation based on modified couple stress theory. International Journal of Structural Stability and Dynamics, 18(9), 1850110 (2018) |
| [19] | ZHANG, L. L., ZHAO, J., NIE, G. Q., and LIU, J. X. Propagation of Rayleigh-type surface waves in a layered piezoelectric nanostructure with surface effects. Applied Mathematics and Mechanics (English Edition), 43(3), 327-340 (2022) https://doi.org/10.1007/s10483-022-2824-7 |
| [20] | FANG, X., WANG, L. Y., LOU, J., FAN, H., ZHANG, A. B., and DU, J. K. A unified model for investigating the propagation of SH surface waves in a piezoelectric layered medium. International Journal of Structural Stability and Dynamics, 24(22), 2450248 (2024) |
| [21] | QI, L. Rayleigh wave propagation in semi-infinite flexoelectric dielectrics. Physica Scripta, 94(6), 065803 (2019) |
| [22] | SHEN, S. P. and HU, S. L. A theory of flexoelectricity with surface effect for elastic dielectrics. Journal of the Mechanics and Physics of Solids, 58(5), 665-677 (2010) |
| [23] | ZHAO, Z. N., ZHU, J., and CHEN, W. Q. Size-dependent vibrations and waves in piezoelectric nanostructures: a literature review. International Journal of Smart and Nano Materials, 13(3), 391-431 (2022) |
| [24] | DE DOMENICO, D., ASKES, H., and AIFANTIS, E. C. Gradient elasticity and dispersive wave propagation: model motivation and length scale identification procedures in concrete and composite laminates. International Journal of Solids and Structures, 158, 176-190 (2019) |
| [25] | JIAO, F. Y., LIU, Z. X., LIU, J. H., and PAN, M. Y. The dispersion and reflection characteristics of coupled waves in the piezomagnetic solid with flexomagnetic microstructure effect. Acta Mechanica, 235, 4101-4117 (2024) |
| [26] | FAFALIS, D. A., FILOPOULOS, S. P., and TSAMASPHYROS, G. J. On the capability of generalized continuum theories to capture dispersion characteristics at the atomic scale. European Journal of Mechanics-A/Solids, 36, 25-37 (2012) |
| [27] | TIERSTEN, H. F. On the nonlinear equations of thermo-electroelasticity. International Journal of Engineering Science, 9(7), 587-604 (1971) |
| [28] | TOUPIN, R. A. The elastic dielectric. Journal of Rational Mechanics and Analysis, 5(6), 849-915 (1956) |
| [29] | KALPAKIDIS, V. K. and MASSALAS, C. V. Tiersten's theory of thermoelectroelasticity: an extension. International Journal of Engineering Science, 31(1), 157-164 (1993) |
| [30] | HU, S. L. and SHEN, S. P. Electric field gradient theory with surface effect for nano-dielectrics. Computers, Materials & Continua, 13(1), 63-87 (2009) |
| [31] | SOLYAEV, Y. and LURIE, S. Electric field, strain and inertia gradient effects on anti-plane wave propagation in piezoelectric materials. Journal of Sound and Vibration, 494, 115898 (2021) |
| [32] | NGUYEN, T. D., MAO, S., YEH, Y. W., PUROHIT, P. K., and MCALPINE, M. C. Nanoscale flexoelectricity. Advanced Materials, 25(7), 946-974 (2013) |
| [33] | YUDIN, P. V. and TAGANTSEV, A. K. Fundamentals of flexoelectricity in solids. Nanotechnology, 24(43), 432001 (2013) |
| [34] | ZUBKO, P., CATALAN, G., and TAGANTSEV, A. K. Flexoelectric effect in solids. Annual Review of Materials Research, 43(1), 387-421 (2013) |
| [35] | NIRWAL, S., SAHU, S. A., SINGHAL, A., and BAROI, J. Analysis of different boundary types on wave velocity in bedded piezo-structure with flexoelectric effect. Composites Part B: Engineering, 167, 434-447 (2019) |
| [36] | YANG, W. J., LIANG, X., DENG, Q., and SHEN, S. P. Rayleigh wave propagation in a homogeneous centrosymmetric flexoelectric half-space. Ultrasonics, 103, 106105 (2020) |
| [37] | HRYTSYNA, O., SLADEK, J., SLADEK, V., DENG, Q., and HRYTSYNA, M. Rayleigh wave propagation in centrosymmetric materials with micro-stiffness, flexoelectric and micro-inertia effects. Ultrasonics, 141, 107317 (2024) |
| [38] | LV, S. H. and SHEN, S. P. Rayleigh waves in a centrosymmetric flexoelectric layer attached to elastic substrate. Acta Mechanica, 234(10), 4649-4664 (2023) |
| [39] | GUPTA, G. and SINGH, B. Static and dynamic flexoelectric effects on wave propagation in microstructured elastic solids. Indian Journal of Physics, 97(5), 1487-1500 (2023) |
| [40] | SAHU, S. A. and BISWAS, M. Mass loading effect on surface wave in piezoelectric-flexoelectric dielectric plate clamped on fiber-reinforced rigid base. International Journal of Mechanics and Materials in Design, 18(4), 919-938 (2022) |
| [41] | ZOU, Y. Y., XIA, Q. G., XU, M. H., LOU, J., ZHANG, M. H., and DU, J. K. Propagation of leaky surface acoustic waves in a layered piezoelectric semiconductor structure. Thin-Walled Structures, 205, 112601 (2024) |
| [42] | XIA, Q. G., ZOU, Y. Y., LOU, J., ZHANG, M. H., and DU, J. K. Effect of initial stresses on propagation of leaky surface acoustic wave in a piezoelectric semiconductor composite structure. Applied Mathematical Modelling, 141, 115908 (2024) |
| [43] | HUTSON, A. R. and WHITE, D. L. Elastic wave propagation in piezoelectric semiconductors. Journal of Applied Physics, 33(1), 40-47 (1962) |
| [44] | TIAN, R., LIU, J. X., PAN, E. N., WANG, Y. S., and SOH, A. K. Some characteristics of elastic waves in a piezoelectric semiconductor plate. Journal of Applied Physics, 126(12), 125701 (2019) |
| [45] | SHARMA, J. N., SHARMA, K. K., and KUMAR, A. Surface waves in a piezoelectric-semiconductor composite structure. International Journal of Solids and Structures, 47(6), 816-826 (2010) |
| [46] | CHEN, Y. M., YANG, L., FANG, X., and WANG, J. Shear-horizontal surface waves in half-space of piezoelectric semiconductor with initial stresses. Acta Physica Polonica Series A, 142, 273-279 (2022) |
| [47] | ZHAO, L. N., WEI, P. J., HUANG, M. S., and XU, Y. Q. Electro-thermo-mechanical multiple fields coupled wave propagation through piezoelectric semiconductor sandwich structure. Composite Structures, 288, 115358 (2022) |
| [48] | WANG, W. H., LI, L., LAN, M., and MA, Z. C. Surface wave speed of functionally gradient piezoelectric semiconductors. Archive of Applied Mechanics, 92(6), 1905-1912 (2022) |
| [49] | YANG, W. J., LIANG, X., and SHEN, S. P. Love waves in layered flexoelectric structures. Philosophical Magazine, 97(33), 3186-3209 (2017) |
| [50] | HASSANZADEH, K., FAROUGHI, S., and KHODAPARAST, H. H. Investigation of guided wave propagation in nanoscale layered periodic piezoelectric plates based on Eringen's nonlocal and strain gradient theory. Applied Mathematical Modelling, 127, 548-570 (2024) |
| [51] | IEŞAN, D. A theory of thermopiezoelectricity with strain gradient and electric field gradient effects. European Journal of Mechanics-A/Solids, 67, 280-290 (2018) |
| [52] | TIAN, R., NIE, G. Q., LIU, J. X., PAN, E. N., and WANG, Y. S. On Rayleigh waves in a piezoelectric semiconductor thin film over an elastic half-space. International Journal of Mechanical Sciences, 204, 106565 (2021) |
| [53] | ROSI, G., PLACIDI, L., and AUFFRAY, N. On the validity range of strain-gradient elasticity: a mixed static-dynamic identification procedure. European Journal of Mechanics-A/Solids, 69, 179-191 (2018) |
| [54] | XU, J., ZHANG, Y. Q., ZHU, J. Y., NEGAHBAN, M., and LI, Z. Flexural wave characteristics in piezoelectric semiconductor beams. Mechanics of Advanced Materials and Structures (2024) https://doi.org/10.1080/15376494.2024.2446714 |
| [55] | YANG, J. S. Analysis of Piezoelectric Semiconductor Structures, Springer, Switzerland (2020) |
| [56] | FANG, X., WANG, L. Y., LOU, J., FAN, H., and DU, J. K. Flexoelectricity and size effects on SH surface waves in a nanoscale piezoelectric semiconductor layered medium. Applied Mathematical Modelling, 141, 115928 (2025) |
| [57] | DU, J. K., CHENG, X. Y., WANG, J., and YONG, Y. K. Rayleigh wave propagating in layered magneto-electro-elastic material structures. 2010 IEEE International Ultrasonics Symposium, Institute of Electrical and Electronics Engineers, San Diego, California, 1179-1182 (2010) |
| [58] | YANG, J. S. A review of a few topics in piezoelectricity. Applied Mechanics Reviews, 59(6), 335-345 (2006) |
| [59] | MINDLIN, R. D. Micro-structure in linear elasticity. Archive for Rational Mechanics and Analysis, 16, 51-78 (1964) |
| [60] | MARANGANTI, R. and SHARMA, P. A novel atomistic approach to determine strain-gradient elasticity constants: tabulation and comparison for various metals, semiconductors, silica, polymers and the (Ir) relevance for nanotechnologies. Journal of the Mechanics and Physics of Solids, 55(9), 1823-1852 (2007) |
| [61] | GUSEV, A. A. and LURIE, S. A. Strain-gradient elasticity for bridging continuum and atomistic estimates of stiffness of binary Lennard-Jones crystals. Advanced Engineering Materials, 12(6), 529-533 (2010) |
| [62] | SHODJA, H. M., ZAHERI, A., and TEHRANCHI, A. Ab initio calculations of characteristic lengths of crystalline materials in first strain gradient elasticity. Mechanics of Materials, 61, 73-78 (2013) |
| [63] | PO, G., LAZAR, M., ADMAL, N. C., and GHONIEM, N. A non-singular theory of dislocations in anisotropic crystals. International Journal of Plasticity, 103, 1-22 (2018) |
| [64] | LAZAR, M. Non-singular dislocation continuum theories: strain gradient elasticity vs. Peierls-Nabarro model. Philosophical Magazine, 97(34), 3246-3275 (2017) |
| [65] | TIERSTEN, H. F. Linear Piezoelectric Plate Vibrations: Elements of the Linear Theory of Piezoelectricity and the Vibrations Piezoelectric Plates, Springer, New York (1969) |
| [66] | SHU, L., WEI, X., PANG, T., YAO, X., and WANG, C. Symmetry of flexoelectric coefficients in crystalline medium. Journal of Applied Physics, 110(10), 104106 (2011) |
| [67] | YANG, W. J., DENG, Q., LIANG, X., and SHEN, S. P. Lamb wave propagation with flexoelectricity and strain gradient elasticity considered. Smart Materials and Structures, 27(8), 085003 (2018) |
| [68] | SLADEK, J., SLADEK, V., WÜNSCHE, M., and ZHANG, C. Z. Effects of electric field and strain gradients on cracks in piezoelectric solids. European Journal of Mechanics-A/Solids, 71, 187-198 (2018) |
| [69] | SOLYAEV, Y. Second gradient continuum model for anisotropic elastic and piezoelectric structures calibrated based on phonon dispersion relations. Mathematics and Mechanics of Solids, 28(10), 2326-2341 (2023) |
| [1] | Xiyan ZOU, Huaiwei HUANG, Xiaohu YAO. Flexoelectric energy dissipating mechanism for multi-impact protection [J]. Applied Mathematics and Mechanics (English Edition), 2025, 46(4): 699-710. |
| [2] | Yabin JING, Lifeng WANG, Yuqiang GAO. Mass-spring model for elastic wave propagation in multilayered van der Waals metamaterials [J]. Applied Mathematics and Mechanics (English Edition), 2024, 45(7): 1107-1118. |
| [3] | Jiajia MAO, Hong CHENG, Tianxue MA. Elastic wave insulation and propagation control based on the programmable curved-beam periodic structure [J]. Applied Mathematics and Mechanics (English Edition), 2024, 45(10): 1791-1806. |
| [4] | Yuan YANG, Nenghui ZHANG, Hanlin LIU, Jiawei LING, Zouqing TAN. Piezoelectric and flexoelectric effects of DNA adsorbed films on microcantilevers [J]. Applied Mathematics and Mechanics (English Edition), 2023, 44(9): 1547-1562. |
| [5] | M. ISHAQ, Hang XU. Nonlinear dynamical magnetosonic wave interactions and collisions in magnetized plasma [J]. Applied Mathematics and Mechanics (English Edition), 2020, 41(8): 1139-1156. |
| [6] | Yanping KONG, Ruomeng TIAN, Jie XU, Jinxi LIU. Propagation behavior of SH waves in a piezomagnetic substrate with an orthorhombic piezoelectric layer [J]. Applied Mathematics and Mechanics (English Edition), 2018, 39(2): 207-218. |
| [7] | Chenyue XIE, Jianjun TAO, Ji LI. Viscous Rayleigh-Taylor instability with and without diffusion effect [J]. Applied Mathematics and Mechanics (English Edition), 2017, 38(2): 263-270. |
| [8] | JIANG Zeng-Rong;DUAN Peng-Fei;GUO Xing-Lin;DING Hua. Improvement of FEM´s dynamic property [J]. Applied Mathematics and Mechanics (English Edition), 2010, 31(11): 1337-1346. |
| [9] | HU Chao;HAN Gang;FANG Xue-qian;HUANG Wen-hu. FLEXURAL WAVE PROPAGATION IN NARROW MINDLIN'S PLATE [J]. Applied Mathematics and Mechanics (English Edition), 2006, 27(6): 793-801 . |
| [10] | Huang Lie-de . THE CAUCHY INTEGRAL OF MANY COMPLEX VARIABLES PASSIVE OPERATORS AND MULTIDIMENSIONAL DISPERSION RELATIONS [J]. Applied Mathematics and Mechanics (English Edition), 1991, 12(7): 687-696. |
| Viewed | ||||||
|
Full text |
|
|||||
|
Abstract |
|
|||||
