Fig. 1

PCBPS configuration: (a) comprising 1× n unit cells, (b) the nonlinear equivalent spring-oscillator system, (c) an oblique view, and (d) front and top views, offering insights into the geometric parameters of the single unit cell (color online)"

Table 1

Primary geometrical parameters"

Fig. 2

(a) Diagram of the PCBPS with the direct lattice vector; (b) reciprocal lattice vector including the IBZ; (c) vibration modes of the unit cells for m1=m2 and m1≠ m2 cases (color online)"

Table 2

Error analyses caused by the M-bar's mass density and the curved beam's height-to-thickness ratio for Case 1: Cutoff frequencies of the pass band for m1=m2 (ρM=1 000 kg/m3)"

Table 3

Error analyses caused by the M-bar's mass density and the curved beam's height-to-thickness ratio for Case 2: Onset frequency and cutoff frequency of the bandgap for m1≠ m2 (Q=3)"

Fig. 3

The switchable and adjustable dispersion relations of PCBPS: the effects of (a) the mass density of the M-bar when Q=3.0 and (b) the curved beam's height-to-thickness ratio when ρM =500 kg/m3 on the onset frequency and the cutoff frequency of the bandgap, the broadened (c) and shifted (d) bandgaps, and (e) the displacement maps corresponding to the cases calculated in (d)(color online)"

Fig. 4

The nonlinear dispersion relations of PCBPs for the cases of (a) m1=m2 and (b) m1≠ m2 (ρM=2 000 kg/m3) (color online)"

Fig. 5

Frequency response curves of the displacement ratio μopt for the system with specified M-bar mass densities:(a) ρM=500 kg/m3 (λ >1), (b) ρM =2 000 kg/m3 (λ < 1), and (c) varying ρM (color online)"

Fig. 6

Effects of the height-to-thickness Q on the frequency response curves of the amplitude ratio for the system with (a)ρM=500 kg/m3 (λ>1) and (b) ρM=2 000 kg/m3 (λ < 1) (color online)"

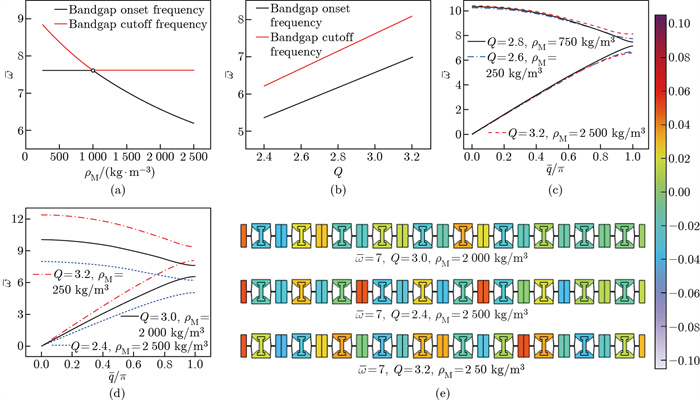
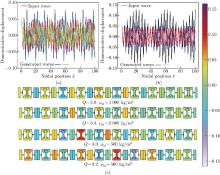
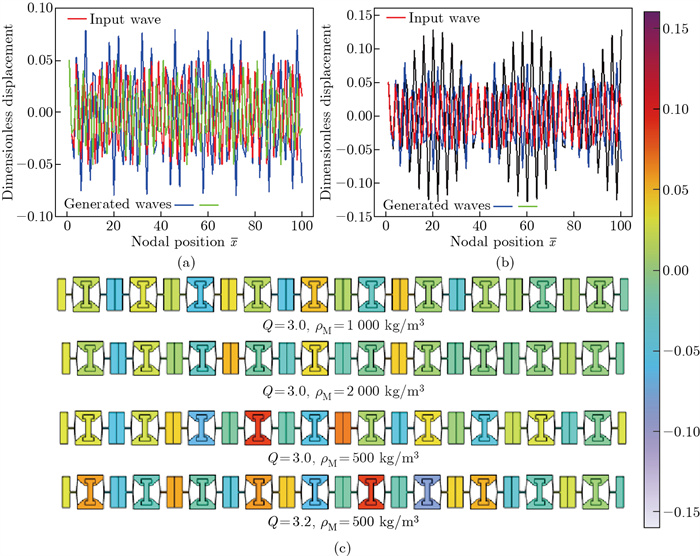
Fig. 7

Responses of the PCBPS excited by the input wave with ω=9: (a) the varying mass density ρM at a fixed height-to-thickness ratio Q, (b) the varying height-to-thickness ratio Q at a fixed mass density ρM, and (c) their corresponding displacement maps, where the red line represents the input wave, and blue, green, and black lines represent the cases of Q=3.0 and ρM =500 kg/m3, Q=3.0 and ρM=2 000 kg/m3, and Q=3.2 and ρM=500 kg/m3, respectively (color online)"