Applied Mathematics and Mechanics (English Edition) ›› 2025, Vol. 46 ›› Issue (3): 423-446.doi: https://doi.org/10.1007/s10483-025-3230-9
Previous Articles Next Articles
Mengru ZHANG1,2, Mingzhu XU1,2, Weiting CHEN1,2,†( ), Yapu ZHAO1,2
), Yapu ZHAO1,2
Received:2024-11-26
Revised:2025-01-16
Published:2025-03-03
Contact:
Weiting CHEN, E-mail: chenweiting@imech.ac.cnSupported by:2010 MSC Number:
Mengru ZHANG, Mingzhu XU, Weiting CHEN, Yapu ZHAO. Thermo-mechanically coupled compatibility conditions in orthogonal curvilinear coordinates: equivalent temperature variation of initially stressed elastomers. Applied Mathematics and Mechanics (English Edition), 2025, 46(3): 423-446.
Fig. 2
Initial stress distributions for parabolic, logarithmic, exponential, hyperelastic, and thermally steady forms: (a) radial initial stress distributions for different κ and a fixed a/b=0.5, (b) radial initial stress distributions for different a/b and a fixed κ/E=0.01, (c) circumferential initial stress distributions for different κ and a fixed a/b=0.5, and (d) circumferential initial stress distributions for different a/b and a fixed κ/E=0.01 (color online)"
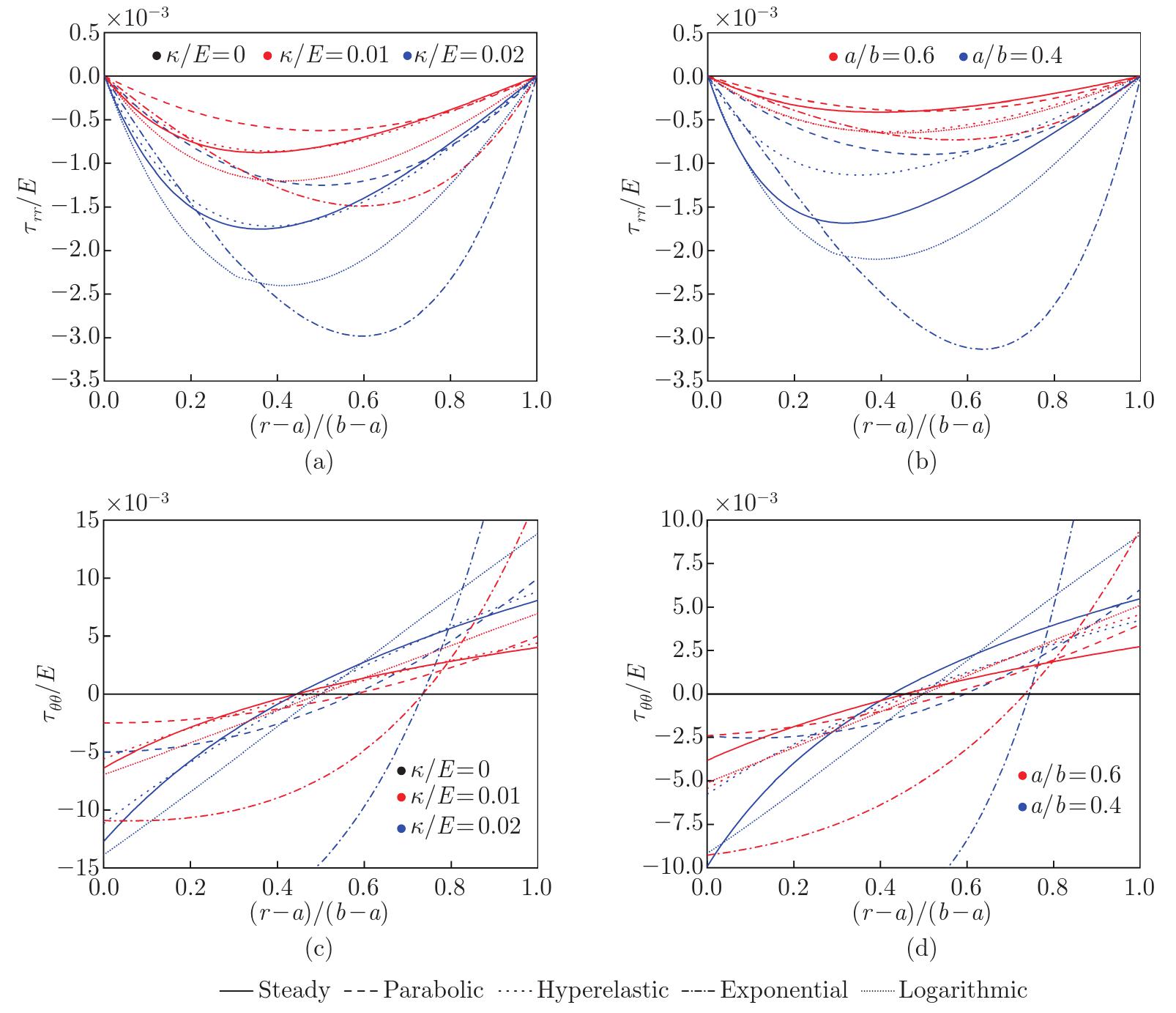
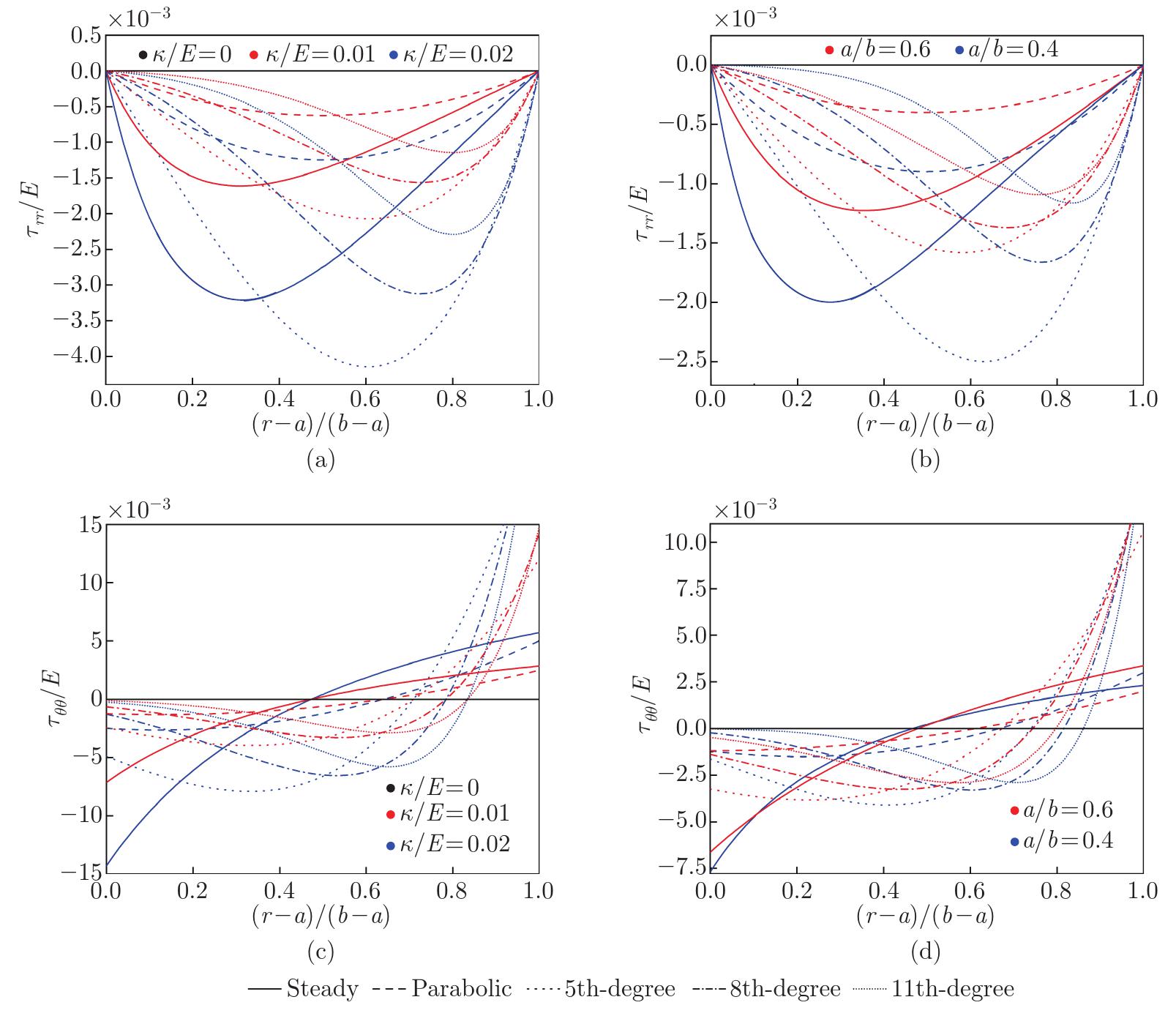
Fig. 4
Initial stress distributions for parabolic, thermally steady, and fifth-, eighth-, and eleventh-degree polynomial forms: (a) radial initial stress distributions for different κ with a fixed a/b=0.5, (b) radial initial stress distributions for different a/b with a fixed κ/E=0.01, (c) circumferential initial stress distributions for different κ with a fixed a/b=0.5, and (d) circumferential initial stress distributions for different a/b with a fixed κ/E=0.01 (color online)"
| [1] | BEATTY, M. F. Topics in finite elasticity: hyperelasticity of rubber, elastomers, and biological tissues — with examples. Applied Mechanics Reviews, 40(12), 1699–1734 (1987) |
| [2] | MARTINEZ, R. V., GLAVAN, A. C., KEPLINGER, C., OYETIBO, A. I., and WHITESIDES, G. M. Soft actuators and robots that are resistant to mechanical damage. Advanced Functional Materials, 24(20), 3003–3010 (2014) |
| [3] | ROGERS, J. A., SOMEYA, T., and HUANG, Y. G. Materials and mechanics for stretchable electronics. Science, 327(5973), 1603–1607 (2010) |
| [4] | CARPI, F., ANDERSON, I., BAUER, S., FREDIANI, G., GALLONE, G., GEI, M., GRAAF, C., JEAN-MISTRAL, C., KAAL, W., KOFOD, G., KOLLOSCH, M., KORNBLUH, R., LASSEN, B., MATYSEK, M., MICHEL, S., NOWAK, S., O'BRIEN, B., PEI, Q., PELRINE, R., RECHENBACH, B., ROSSET, S., and SHEA, H. Standards for dielectric elastomer transducers. Smart Materials and Structures, 24(10), 105025 (2015) |
| [5] | BUSTAMANTE, R., SHARIFF, M. H. B. M., and HOSSAIN, M. Mathematical formulations for elastic magneto-electrically coupled soft materials at finite strains: time-independent processes. International Journal of Engineering Science, 159, 103429 (2021) |
| [6] | SHARIFF, M. H. B. M., MERODIO, J., and BUSTAMANTE, R. Nonlinear elastic constitutive relations of residually stressed composites with stiff curved fibres. Applied Mathematics and Mechanics (English Edition), 43(10), 1515–1530 (2022) https://doi.org/10.1007/s10483-022-2910-7 |
| [7] | GAO, Y., LI, B., WANG, J. S., and FENG, X. Q. Fracture toughness analysis of helical fiber-reinforced biocomposites. Journal of the Mechanics and Physics of Solids, 146, 104206 (2021) |
| [8] | YIN, S. F., LI, B., and FENG, X. Q. Bio-chemo-mechanical theory of active shells. Journal of the Mechanics and Physics of Solids, 152, 104419 (2021) |
| [9] | WANG, X. H., HUANG, X. F., LIN, K., and ZHAO, Y. P. The constructions and pyrolysis of 3D kerogen macromolecular models: experiments and simulations. Global Challenges, 3(5), 1900006 (2019) |
| [10] | WANG, X. H. and ZHAO, Y. P. The time-temperature-maturity relationship: a chemical kinetic model of kerogen evolution based on a developed molecule-maturity index. Fuel, 278, 118264 (2020) |
| [11] | WANG, X. H., HUANG, X. F., GAO, M. N., and ZHAO, Y. P. Mechanical response of kerogen at high strain rates. International Journal of Impact Engineering, 155, 103905 (2021) |
| [12] | CHEN, W. T. and ZHAO, Y. P. Thermo-mechanically coupled constitutive equations for soft elastomers with arbitrary initial states. International Journal of Engineering Science, 178, 103730 (2022) |
| [13] | CHEN, W. T. and ZHAO, Y. P. Hyperelastic constitutive relations for soft elastomers with thermally-induced residual stress. International Journal of Engineering Science, 195, 103991 (2024) |
| [14] | CHEN, W. T., HUANG, X. F., YUAN, Q. Z., and ZHAO, Y. P. Initially stressed strain gradient elasticity: a constitutive model incorporates size effects and initial stresses. International Journal of Engineering Science, 205, 104166 (2024) |
| [15] | DING, L. Q., WANG, Z. Q., LV, J. G., WANG, Y., and LIU, B. L. A new model for real-time prediction of wellbore stability considering elastic and strength anisotropy of bedding formation. Energies, 15(1), 251 (2022) |
| [16] | TRUESDELL, C. Das ungelöste hauptproblem der endlichen elastizitätstheorie. Journal of Applied Mathematics and Mechanics, 36(3-4), 97–103 (1956) |
| [17] | ZHAO, Y. P. Modern Continuum Mechanics, Science Press, Beijing (2018) |
| [18] | MOONEY, M. A theory of large elastic deformation. Journal of Applied Physics, 11(9), 582–592 (1940) |
| [19] | RIVLIN, R. S. Large elastic deformations of isotropic materials, IV, further developments of the general theory. Philosophical Transactions of the Royal Society of London. Series A, Mathematical and Physical Sciences, 241(835), 379–397 (1948) |
| [20] | RAJAGOPAL, K. R. and SACCOMANDI, G. A novel approach to the description of constitutive relations. Frontiers in Materials, 3, 36 (2016) |
| [21] | DAL, H., AÇIKGÖZ, K., and BADIENIA, Y. On the performance of isotropic hyperelastic constitutive models for rubber-Like materials: a state of the art review. Applied Mechanics Reviews, 73(2), 020802 (2021) |
| [22] | ZHU, F. W., DUI, G. S., and REN, Q. W. A continuum model of jointed rock masses based on micromechanics and its integration algorithm. Science China Technological Sciences, 54(3) 581–590 (2011) |
| [23] | CHUONG, C. J. and FUNG, Y. C. Three-dimensional stress distribution in arteries. Journal of Biomechanical Engineering, 105(3), 268–274 (1983) |
| [24] | WITHERS, P. J. and BHADESHIA, H. K. D. H. Residual stress, part 2: nature and origins. Materials Science and Technology, 17(4), 366–375 (2001) |
| [25] | HOLZAPFEL, G. A. and OGDEN, R. W. Mechanics of Biological Tissue, Springer-Verlag, Berlin (2006) |
| [26] | HOSFORD, W. F. Mechanical Behavior of Materials, Cambridge University Press, Cambridge (2010) |
| [27] | ZANG, A. and STEPHANSSON, O. Stress Field of the Earth's Crust, Springer Science & Business Media, Berlin (2010) |
| [28] | CHEN, Y. C. and EBERTH, J. F. Constitutive function, residual stress, and state of uniform stress in arteries. Journal of the Mechanics and Physics of Solids, 60(6), 1145–1157 (2012) |
| [29] | STYLIANOPOULOS, T., MARTIN, J. D., CHAUHAN, V. P., JAIN, S. R., DIOP-FRIMPONG, B., BARDEESY, N., SMITH, B. L., FERRONE, C. R., HORNICEK, F. J., BOUCHER, Y., MUNN, L. L., and JAIN, R. K. Causes, consequences, and remedies for growth-induced solid stress in murine and human tumors. Proceedings of the National Academy of Sciences, 109(38), 15101–15108 (2012) |
| [30] | HEIDBACH, O., RAJABI, M., CUI, X. F., FUCHS, K., MÜLLER, B., REINECKER, J., REITER, K., TINGAY, M., WENZEL, F., XIE, F. R., ZIEGLER, M. O., ZOBACK, M. L., and ZOBACK, M. The world stress map database release 2016: crustal stress pattern across scales. Tectonophysics, 744, 484–498 (2018) |
| [31] | WEBSTER, G. A. and EZEILO, A. N. Residual stress distributions and their influence on fatigue lifetimes. International Journal of Fatigue, 23, 375–383 (2001) |
| [32] | SHEN, W. H. and ZHAO, Y. P. Combined effect of pressure and shear stress on penny-shaped fluid-driven cracks. Journal of Applied Mechanics, 85(3), 031003 (2018) |
| [33] | SUN, F. Q., SHEN, W. H., and ZHAO, Y. P. Deflected trajectory of a single fluid-driven crack under anisotropic in-situ stress. Extreme Mechanics Letters, 29, 100483 (2019) |
| [34] | MONAJEMI, A. A. and MOHAMMADIMEHR, M. Effects of residual stress and viscous and hysteretic dampings on the stability of a spinning micro-shaft. Applied Mathematics and Mechanics (English Edition), 41(8), 1251–1268 (2020) https://doi.org/10.1007/s10483-020-2640-8 |
| [35] | CHEN, J., WANG, Y. W., and LI, X. F. Antiplane shear crack in a prestressed elastic medium based on the couple stress theory. Applied Mathematics and Mechanics (English Edition), 44(4), 583–602 (2023) https://doi.org/10.1007/s10483-023-2977-6 |
| [36] | FUNG, Y. C. What are the residual stresses doing in our blood vessels? Annals of Biomedical Engineering, 19(3), 237–249 (1991) |
| [37] | AMAR, M. B. and GORIELY, A. Growth and instability in elastic tissues. Journal of the Mechanics and Physics of Solids, 53(10), 2284–2319 (2005) |
| [38] | LI, B., CAO, Y. P., FENG, X. Q., and GAO, H. J. Surface wrinkling of mucosa induced by volumetric growth: theory, simulation and experiment. Journal of the Mechanics and Physics of Solids, 59(4), 758–774 (2011) |
| [39] | NAM, K., PARK, I., and KO, S. Patterning by controlled cracking. nature, 485(7397), 221–224 (2012) |
| [40] | DU, Y. K., LÜ, C. F., DESTRADE, M., and CHEN, W. Q. Influence of initial residual stress on growth and pattern creation for a layered aorta. Scientific Reports, 9(1), 1–9 (2019) |
| [41] | HOGER, A. On the residual stress possible in an elastic body with material symmetry. Archive for Rational Mechanics and Analysis, 88(3), 271–289 (1985) |
| [42] | HOGER, A. On the determination of residual stress in an elastic body. Journal of Elasticity, 16(3), 303–324 (1986) |
| [43] | HUANG, X. F., LIU, Z. W., and XIE, H. M. Recent progress in residual stress measurement techniques. Acta Mechanica Solida Sinica, 26(6), 570–583 (2013) |
| [44] | GRECO, A., SGAMBITTERRA, E., and FURGIUELE, F. A new methodology for measuring residual stress using a modified Berkovich nano-indenter. International Journal of Mechanical Sciences, 207, 106662 (2021) |
| [45] | LI, X. W., LIU, J. W., WU, H., MIAO, K. S., WU, H., LI, R. G., LIU, C. L., FANG, W. B., and FAN, G. H. Research progress of residual stress measurement methods. Heliyon, 10(7), e28348 (2024) |
| [46] | LI, Z. Q., CUI, C. C., ARTEAGA, O., BIAN, S. B., TONG, H., LU, J., and XU, X. P. Full-field measurement of residual stress in single-crystal diamond substrates based on Mueller matrix microscopy. Measurement, 234, 114790 (2024) |
| [47] | MOON, S., CHOI, M., HONG, S., KIM, S. W., and YOON, M. Non-equibiaxial residual stress evaluation methodology using simulated indentation behavior and machine learning. Nuclear Engineering and Technology, 56(4), 1347–1356 (2024) |
| [48] | ZHOU, H. M., SUN, Q., XI, G. D., and LI, D. Q. Numerical prediction of process-induced residual stresses in glass bulb panel. Applied Mathematics and Mechanics (English Edition), 27(9), 1197–1206 (2006) https://doi.org/10.1007/s10483-006-0906-z |
| [49] | CHEN, Y. C. and HOGER, A. Constitutive functions of elastic materials in finite growth and deformations. Journal of Elasticity, 59, 175–193 (2000) |
| [50] | SARAVANAN, U. Representation for stress from a stressed reference configuration. International Journal of Engineering Science, 46(11), 1063–1076 (2008) |
| [51] | RODRIGUEZ, E. K., HOGER, A., and MCCULLOCH, A. D. Stress-dependent finite growth in soft elastic tissues. Journal of Biomechanics, 27(4), 455–467 (1994) |
| [52] | HOLZAPFEL, G. A., GASSER, T. C., and OGDEN, R. W. A new constitutive framework for arterial wall mechanics and a comparative study of material models. Journal of Elasticity, 61, 1–48 (2000) |
| [53] | DU, Y. K., LÜ, C. F., CHEN, W. Q., and DESTRADE, M. Modified multiplicative decomposition model for tissue growth: beyond the initial stress-free state. Journal of the Mechanics and Physics of Solids, 118, 133–151 (2018) |
| [54] | RAUSCH, M. K. and KUHL, E. On the effect of prestrain and residual stress in thin biological membranes. Journal of the Mechanics and Physics of Solids, 61(9), 1955–1969 (2013) |
| [55] | CHESTER, S. A. and ANAND, L. A thermo-mechanically coupled theory for fluid permeation in elastomeric materials: application to thermally responsive gels. Journal of the Mechanics and Physics of Solids, 59(10), 1978–2006 (2011) |
| [56] | ZHANG, M. R., CHEN, W. T., HUANG, X. F., YUAN, Q. Z., and ZHAO, Y. P. Hyperelastic constitutive relations for porous materials with initial stress. Journal of the Mechanics and Physics of Solids, 193, 105886 (2024) |
| [57] | REINA, C., DJODOM, L. F., ORTIZ, M., and CONTI, S. Kinematics of elasto-plasticity: validity and limits of applicability of F = FeFp for general three-dimensional deformations. Journal of the Mechanics and Physics of Solids, 121, 99–113 (2018) |
| [58] | YANG, F. Q., LI, Y., and ZHANG, K. A multiplicative finite strain deformation for diffusion-induced stress: an incremental approach. International Journal of Engineering Science, 187, 103841 (2023) |
| [59] | MUKHERJEE, S. and RAVINDRAN, P. Representation of stress and free energy for a viscoelastic body from a stressed reference. Journal of the Mechanics and Physics of Solids, 184, 105544 (2024) |
| [60] | SADAGOAPAN, T. S., RAVINDRAN, P., and MURTHY, H. S. N. A continuum model for predicting strain evolution in carbon fiber-reinforced composites subjected to cyclic loading. Sādhanā, 47(3), 1–9 (2022) |
| [61] | YAVARI, A. and SOZIO, F. On the direct and reverse multiplicative decompositions of deformation gradient in nonlinear anisotropic anelasticity. Journal of the Mechanics and Physics of Solids, 170, 105101 (2023) |
| [62] | SU, H. D., YAN, H. X., and JIN, B. Finite element method for coupled diffusion-deformation theory in polymeric gel based on slip-link model. Applied Mathematics and Mechanics (English Edition), 39(4), 581–596 (2018) https://doi.org/10.1007/s10483-018-2315-7 |
| [63] | DU, Y. K., SU, Y. P., LÜ, C. F., CHEN, W. Q., and DESTRADE, M. Electro-mechanically guided growth and patterns. Journal of the Mechanics and Physics of Solids, 143, 104073 (2020) |
| [64] | HOGER, A. Virtual configurations and constitutive equations for residually stressed bodies with material symmetry. Journal of Elasticity, 48(2), 125–144 (1997) |
| [65] | JOHNSON, B. E. and HOGER, A. The dependence of the elasticity tensor on residual stress. Journal of Elasticity, 33(2), 145–165 (1993) |
| [66] | JOHNSON, B. E. and HOGER, A. The use of a virtual configuration in formulating constitutive equations for residually stressed elastic materials. Journal of Elasticity, 41(3), 177–215 (1995) |
| [67] | JOHNSON, B. E. and HOGER, A. The use of strain energy to quantify the effect of residual stress on mechanical behavior. Mathematics and Mechanics of Solids, 3(4), 447–470 (1998) |
| [68] | LEV, Y., FAYE, A., and VOLOKH, K. Y. Thermoelastic deformation and failure of rubberlike materials. Journal of the Mechanics and Physics of Solids, 122, 538–554 (2019) |
| [69] | FUHG, J. N., JADOON, A., WEEGER, O., SEIDL, D. T., and JONES, R. E. Polyconvex neural network models of thermoelasticity. Journal of the Mechanics and Physics of Solids, 192, 105837 (2024) |
| [70] | YAVARI, A. Compatibility equations of nonlinear elasticity for non-simply-connected bodies. Archive for Rational Mechanics and Analysis, 209(1), 237–253 (2013) |
| [71] | FOSDICK, R. L. Modern Developments in the Mechanics of Continua, Academic Press, London (1966) |
| [72] | CESÀRO, E. Sulle formule del Volterra, fondamentali nella teoria delle distorsioni elastiche. Il Nuovo Cimento (1901-1910), 12(1), 143–154 (1906) |
| [73] | VOLTERRA, V. Sur l'équilibre des corps élastiques multiplement connexes. Annales scientifiques de l'École Normale Supérieure, 24, 401–517 (1907) |
| [74] | CIARLET, P. G., GRATIE, L., and MARDARE, C. A generalization of the classical Cesàro-Volterra path integral formula. Comptes Rendus. Mathématique, 347(9-10), 577–582 (2009) |
| [75] | CIARLET, P. G., GRATIE, L., and MARDARE, C. A Cesàro-Volterra formula with litte regularity. Journal de Mathématiques Pures et Appliquées, 93(1), 41–60 (2010) |
| [76] | BARRETTA, R. On Cesàro-Volterra method in orthotropic Saint-Venant beam. Journal of Elasticity, 112(2), 233–253 (2013) |
| [77] | FOSDICK, R. and ROYER-CARFAGNI, G. Hadamard's conditions of compatibility from Cesaro's line-integral representation. International Journal of Engineering Science, 146, 103174 (2020) |
| [78] | SKALAK, R., ZARGARYAN, S., JAIN, R. K., NETTI, P. A., and HOGER, A. Compatibility and the genesis of residual stress by volumetric growth. Journal of Mathematical Biology, 34(8), 889–914 (1996) |
| [79] | LANIR, Y. Mechanisms of residual stress in soft tissues. Journal of Biomechanical Engineering, 131(4), 044506 (2009) |
| [80] | ZAZA, D., CIAVARELLA, M., and ZURLO, G. Strain incompatibility as a source of residual stress in welding and additive manufacturing. European Journal of Mechanics-A/Solids, 85, 104147 (2021) |
| [81] | AMROUCHE, C., CIARLET, P. G., GRATIE, L., and KESAVAN, S. On Saint Venant's compatibility conditions and Poincare's lemma. Comptes Rendus Mathématique, 342(11), 887–891 (2006) |
| [82] | BORODACHEV, N. M. The equations of compatibility of deformations. Journal of Applied Mathematics and Mechanics, 65(6), 1021–1024 (2001) |
| [83] | LEE, C. W. Thermoelastic stresses in thick-walled cylinders under axial temperature gradient. Journal of Applied Mechanics, 33(2), 467–469 (1966) |
| [84] | MUTI, S. and DOKUZ, M. S. Two-dimensional Beltrami-Michell equations for a mixture of two linear elastic solids and some applications using the Airy stress function. International Journal of Solids and Structures, 59, 140–146 (2015) |
| [85] | TEODORESCU, P. P. On Beltrami-Michell and Beltrami-Michell type equations. Mechanics Research Communications, 3(6), 475–482 (1976) |
| [86] | VALLÉE, C. and FORTUNÉ, D. Compatibility equations in shell theory. International Journal of Engineering Science, 34(5), 495–499 (1996) |
| [87] | ARGATOV, I. I., JIN, X. Q., and KEER, L. M. Depth-sensing spherical indentation of an elastic sphere on an elastic substrate. Journal of the Mechanics and Physics of Solids, 149, 104297 (2021) |
| [88] | WAHYUDI, H., CHU, K. W., and YU, A. B. 3D particle-scale modeling of gas-solids flow and heat transfer in fluidized beds with an immersed tube. International Journal of Heat and Mass Transfer, 97, 521–537 (2016) |
| [89] | OLSEN, T., KASPER, T., and DE WIT, J. Immersed tunnels in soft soil conditions experience from the last 20 years. Tunnelling and Underground Space Technology, 121, 104315 (2022) |
| [90] | HELMS, F., HAVERICH, A., BÖER, U., and WILHELMI, M. Transluminal compression increases mechanical stability, stiffness and endothelialization capacity of fibrin-based bioartificial blood vessels. Journal of the Mechanical Behavior of Biomedical Materials, 124, 104835 (2021) |
| [91] | ENOMOTO, T., MAO, X., and SATAKE, U. Cutting performance by surgical scissors of tubular soft tissues such as blood vessels. CIRP Annals, 70(1), 69–72 (2021) |
| [92] | CHENG, Y., YANG, H. W., XU, Z. Y., and LU, C. P. Cavity expansion analysis of normal indention of rocks with lateral confinement. Computers and Geotechnics, 145, 104693 (2022) |
| [93] | FARQUHAR, M. E., BURRAGE, K., SANTOS, R. W. D., BUENO-OROVIO, A., and LAWSON, B. A. J. Graph-based homogenisation for modelling cardiac fibrosis. Journal of Computational Physics, 459, 111126 (2022) |
| [94] | BELHAMADIA, Y., BRIFFARD, T., and FORTIN, A. Efficiency of parallel anisotropic mesh adaptation for the solution of the bidomain model in cardiac tissue. Journal of Computational Science, 61, 101656 (2022) |
| [95] | CIARLETTA, P., DESTRADE, M., GOWER, A. L., and TAFFETANI, M. Morphology of residually stressed tubular tissues: beyond the elastic multiplicative decomposition. Journal of the Mechanics and Physics of Solids, 90, 242–253 (2016) |
| [96] | MERODIO, J. and OGDEN, R. W. Extension, inflation and torsion of a residually stressed circular cylindrical tube. Continuum Mechanics and Thermodynamics, 28, 157–174 (2016) |
| [97] | MELNIKOV, A., OGDEN, R. W., DORFMANN, L., and MERODIO, J. Bifurcation analysis of elastic residually-stressed circular cylindrical tubes. International Journal of Solids and Structures, 226-227, 111062 (2021) |
| [98] | HOLZAPFEL, G. A. and OGDEN, R. W. Biomechanics of Soft Tissue in Cardiovascular Systems, Springer-Verlag, Vienna (2003) |
| [99] | YUCESOY, A. and PENCE, T. J. On the inflation of residually stressed spherical shells. Journal of Elasticity, 151(1), 107–126 (2022) |
| [100] | KACHANOV, M., SHAFIRO, B., and TSUKROV, I. Handbook of Elasticity Solutions, Springer Science & Business Media, Dordrecht (2003) |
| [101] | SEDOV, L. I. Foundations of the Non-Linear Mechanics of Continua, Pergamon Press, Oxford (1966) |
| [102] | CIARLET, P. G., CRISTINEL, M., and SHEN, M. Saint Venant compatibility equations in curvilinear coordinates. Analysis and Applications, 5(3), 231–251 (2007) |
| [103] | VLASOV, V. Z. The equations of continuity of deformations in curvilinear coordinates. Prikladnaya Matematika i Mekhanika, 8, 301 (1944) |
| [104] | BRDIČKA, M. The equations of compatibility and stress functions in tensor form. Czechoslovak Journal of Physics, 3(1), 52 (1953) |
| [105] | BARREKETTE, E. S. Stress compatibility equations in cylindrical coordinates. AIAA Journal, 6(4), 767–767 (1968) |
| [106] | TUBA, I. S. Compatibility equations for arbitrary orthogonal curvilinear coordinates. AIAA Journal, 4(9), 1695–1696 (1966) |
| [107] | ERINGEN, A. C. Mechanics of Continua, Robert E. Krieger Publishing Company, New York (1980) |
| [108] | JOG, C. S. The equations of equilibrium in orthogonal curvilinear reference coordinates. Journal of Elasticity, 104, 385–395 (2011) |
| [109] | LUBARDA, V. A. Remarks on axially and centrally symmetric elasticity problems. International Journal of Engineering Science, 47(4), 642–647 (2009) |
| [110] | BUSTAMANTE, R. and RAJAGOPAL, K. R. Modelling residual stresses in elastic bodies described by implicit constitutive relations. International Journal of Non-Linear Mechanics, 105, 113–129 (2018) |
| [111] | CIARLETTA, P., DESTRADE, M., and GOWER, A. On residual stresses and homeostasis: an elastic theory of functional adaptation in living matter. Scientific Reports, 6(1), 24390 (2016) |
| [112] | OGDEN, R. W. and SCHULZE-BAUER, C. A. J. Phenomenological and structural aspects of the mechanical response of arteries, ASME International Mechanical Engineering Congress and Exposition, American Society of Mechanical Engineers, New York, 125–140 (2000) |
| [1] | Lingyun GUO, Yizhan YANG, Wanli YANG, Yuantai HU. The action mechanism of the work done by the electric field force on moving charges to stimulate the emergence of carrier generation/recombination in a PN junction [J]. Applied Mathematics and Mechanics (English Edition), 2024, 45(6): 1001-1014. |
| [2] | Jian CHEN, Yawei WANG, Xianfang LI. Antiplane shear crack in a prestressed elastic medium based on the couple stress theory [J]. Applied Mathematics and Mechanics (English Edition), 2023, 44(4): 583-602. |
| [3] | Zhenni LI, Yize WANG, Yuesheng WANG. Tunable three-dimensional nonreciprocal transmission in a layered nonlinear elastic wave metamaterial by initial stresses [J]. Applied Mathematics and Mechanics (English Edition), 2022, 43(2): 167-184. |
| [4] | A. E. ABOUELREGAL. Size-dependent thermoelastic initially stressed micro-beam due to a varying temperature in the light of the modified couple stress theory [J]. Applied Mathematics and Mechanics (English Edition), 2020, 41(12): 1805-1820. |
| [5] | K. K. PANKAJ, S. A. SAHU, S. KUMARI. Surface wave transference in a piezoelectric cylinder coated with reinforced material [J]. Applied Mathematics and Mechanics (English Edition), 2020, 41(1): 123-138. |
| [6] | S. M. ABO-DAHAB, A. M. ABD-ALLA, A. A. KILANY. Effects of rotation and gravity on an electro-magneto-thermoelastic medium with diffusion and voids by using the Lord-Shulman and dual-phase-lag models [J]. Applied Mathematics and Mechanics (English Edition), 2019, 40(8): 1135-1154. |
| [7] | S. K. VISHWAKARMA, R. KAUR, T. R. PANIGRAHI. Torsional wave frequency in heterogeneous earth crust lying over dry sandy semi-infinite substratum [J]. Applied Mathematics and Mechanics (English Edition), 2019, 40(10): 1399-1412. |
| [8] | P. SINGH, A. CHATTOPADHYAY, A. K. SINGH. Rayleigh-type wave propagation in incompressible visco-elastic media under initial stress [J]. Applied Mathematics and Mechanics (English Edition), 2018, 39(3): 317-334. |
| [9] | P. ALAM, S. KUNDU, S. GUPTA. Dispersion and attenuation of torsional wave in a viscoelastic layer bonded between a layer and a half-space of dry sandy media [J]. Applied Mathematics and Mechanics (English Edition), 2017, 38(9): 1313-1328. |
| [10] | Wei LIU, Baohua YU, Jingen DENG. Analytical method for evaluating stress field in casing-cementformation system of oil/gas wells [J]. Applied Mathematics and Mechanics (English Edition), 2017, 38(9): 1273-1294. |
| [11] | Bohua SUN. Incompatible deformation field and Riemann curvature tensor [J]. Applied Mathematics and Mechanics (English Edition), 2017, 38(3): 311-332. |
| [12] | S. GUPTA;S. K. VISHWAKARMA. Propagation of P- and S-waves in initially stressed gravitating half space [J]. Applied Mathematics and Mechanics (English Edition), 2013, 34(7): 847-860. |
| [13] | S. GUPTA; D. K. MAJHI; S. KUNDU; S. K. VISHWAKARMA. Propagation of Love waves in non-homogeneous substratum over initially stressed heterogeneous half-space [J]. Applied Mathematics and Mechanics (English Edition), 2013, 34(2): 249-258. |
| [14] | S.Gupta;A.Chattopadhyay;D.K.Majhi. Effect of irregularity on the propagation of torsional surface waves in an initially stressed anisotropic poro-elastic layer [J]. Applied Mathematics and Mechanics (English Edition), 2010, 31(4): 481-492. |
| Viewed | ||||||
|
Full text |
|
|||||
|
Abstract |
|
|||||


 Email Alert
Email Alert RSS
RSS