Applied Mathematics and Mechanics (English Edition) ›› 2025, Vol. 46 ›› Issue (8): 1433-1450.doi: https://doi.org/10.1007/s10483-025-3282-9
Previous Articles Next Articles
Qinghua ZHU1, Fang HAN2,3,†( ), Qingyun WANG2,4
), Qingyun WANG2,4
Received:2025-01-19
Revised:2025-06-09
Published:2025-07-28
Contact:
Fang HAN, E-mail: yadiahan@dhu.edu.cnSupported by:2010 MSC Number:
Qinghua ZHU, Fang HAN, Qingyun WANG. A spinal circuit model with an asymmetric cervical-lumbar layout for limb coordination and gait control in quadrupeds. Applied Mathematics and Mechanics (English Edition), 2025, 46(8): 1433-1450.
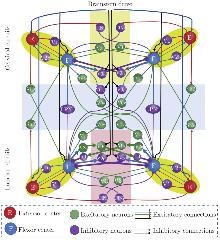
Fig. 1
Model framework of the quadrupedal spinal circuits with an asymmetric cervical-lumbar layout. The model includes four RGs, each consisting of one flexor center (F) and one extensor center (E). E and F are coupled through inhibitory projections provided by V2b and V1 neurons and direct excitatory projections. Left-right alternation in the cervical circuit is mediated through the V0D pathway, whereas left-right alternation in the lumbar circuit is mediated through the IV2a-V0V and V0D pathways (highlighted with thicker lines). Left-right synchronization is controlled via the V3 and CINi CIN pathways. Cervical-lumbar coordination is controlled via descending or ascending the Shox2, LPNi, V0D, IIV2a-V0V, and IV2a-V0V LPNs pathways. E and F receive constant (blue lines) and linearly changed (black lines) brainstem drives, respectively. Also, inhibitory CIN and LPN circuits receive inhibitory brainstem drives. Here, cervical and lumbar CINs are highlighted with light yellow and light pink shades, respectively. The model framework is modified from Danner et al.[27] (color online)"
Table 1
Neuron model parameters"
| Parameter | Value |
|---|---|
| Membrane capacitance | |
| Maximal conductance | |
| Reversal potential | |
| Threshold/maximum voltage | |
| Half-voltage | |
| Slope | |
| Time constant |
Table 3
Connection weights"
| Scope | Source | Target ( |
|---|---|---|
| Within cervical and lumber circuits | F | E (0.01), V2b (4.0), V3 (3.5), |
| E | F (0.01), V1 (4.0), Sh2 (5.0), CINi (4.0) | |
| V1 | F | |
| V2b | E | |
| CINi | F | |
| V3 | F (0.3) | |
| Within cervical circuits | c-F | LPNi (7.0), IIV2a-diag (5.0), |
| c-F | ||
| IIV2a-diag | ||
| Within lumber circuits | l-F | IV2a (10.0), IV2a-diag (5.0) |
| IV2a | ||
| InI (6.0) | ||
| InI | l-F | |
| l-F | ||
| IV2a-diag | ||
| Between cervical-lumber homolateral circuits | c-Sh2 | l-F (0.1) |
| l-Sh2 | c-F (1.25) | |
| LPNi | l-F | |
| Between cervical-lumber diagonal circuits | l-F | |
| c- | l-F (0.2) | |
| l- | c-F (0.1) |
Table 4
Gait definitions"
| Gait | Left-right fore | Left-right hind | Homolateral | Diagonal |
|---|---|---|---|---|
| Walk | [0.25,0.75] | [0.25,0.75] | [0.1,0.4)/(0.6,0.9] | [0.1,0.4)/(0.6,0.9] |
| Trot | [0.25,0.75] | [0.25,0.75] | [0.25,0.75] | [0.0,0.1]/[0.9,1.0] |
| Gallop | [0.25,0.75] | (0.0,0.25]/[0.75,1.0) | [0.25,0.75] | (0.15,0.4)/(0.6,0.85) |
| Bound | [0.0,0.025]/(0.975,1.0] | [0.0,0.025]/(0.975,1.0] | [0.25,0.75] | [0.25,0.75] |
Fig. 2
Dynamical performances of RG neurons regulated by the brainstem drive and ionic currents. (a) The bifurcation diagram of V with respect to α, where red, black, and blue lines represent stable equilibria, unstable equilibria, and stable limit cycles, respectively. The limit cycles occur when α falls within the range of [0, 0.953 4] (horizontal black bar). HB denotes the Hopf bifurcation point. (b)–(d) Burst (diamond), interburst (square) durations, and oscillation frequency (triangle) as functions of (b) α, (c) gM, and (d) gNaP (color online)"
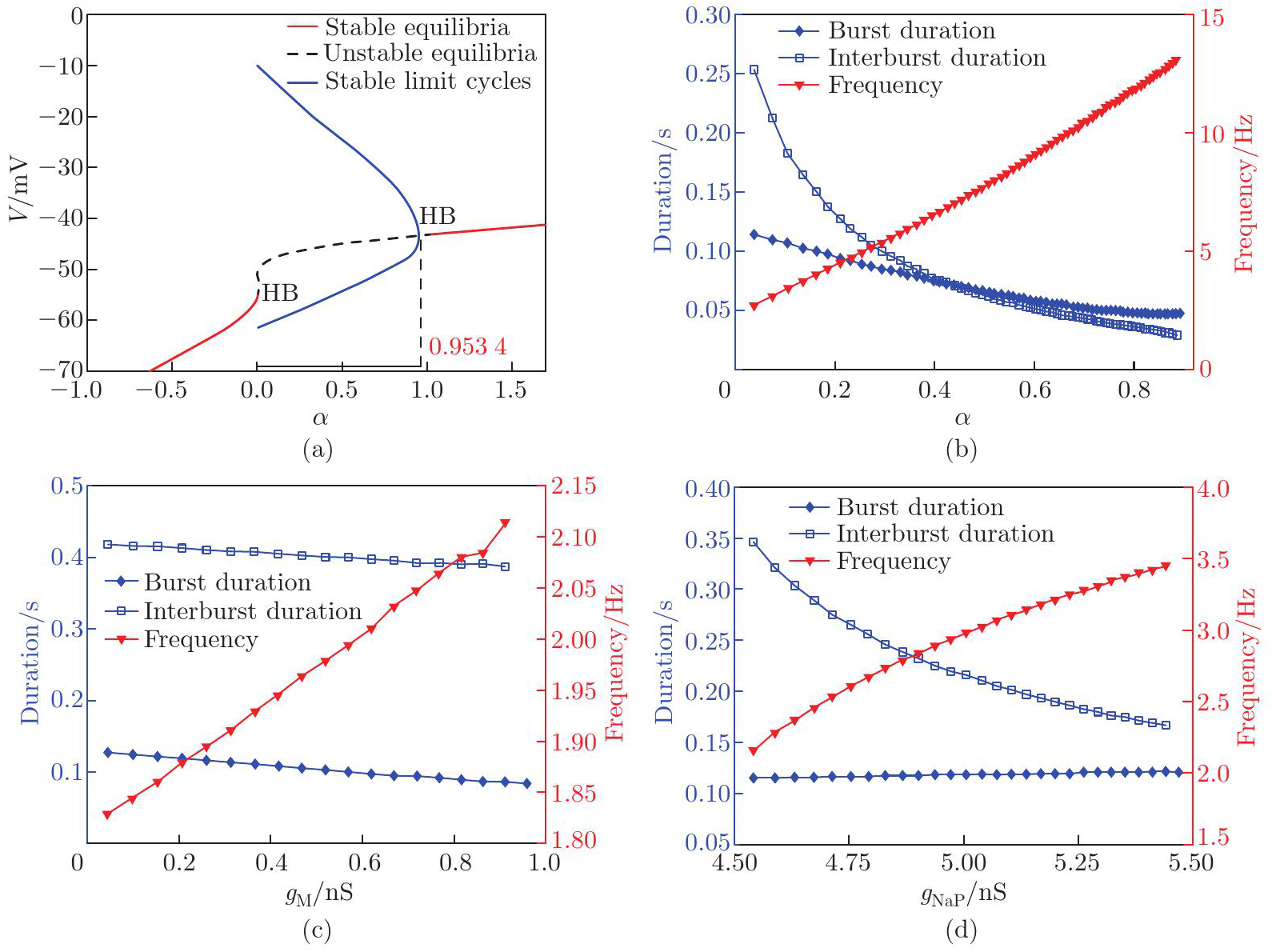
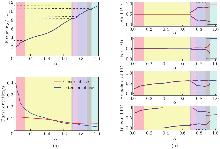
Fig. 3
Performance of the model regulated by the brainstem drive. (a) Locomotor frequency (the top panel) and phase duration (the bottom panel) as functions of α; (b) PDs of the hindlimbs (the top panel), forelimbs (the second panel), homolateral (the third panel), and diagonal (the bottom panel) as functions of α. Blue and red lines represent stable PDs when increasing and decreasing the bifurcation parameter α, respectively. Colored areas represent the gaits expressed in the corresponding intervals of α: red for walk, yellow for trot, blue for gallop, green for bound, gray for bistability, and pink for undefined. The blue-shaded area marked by the black dashed box represents a more biologically appropriate gallop gait. Hind: hindlimbs; Fore: forelimbs (color online)"
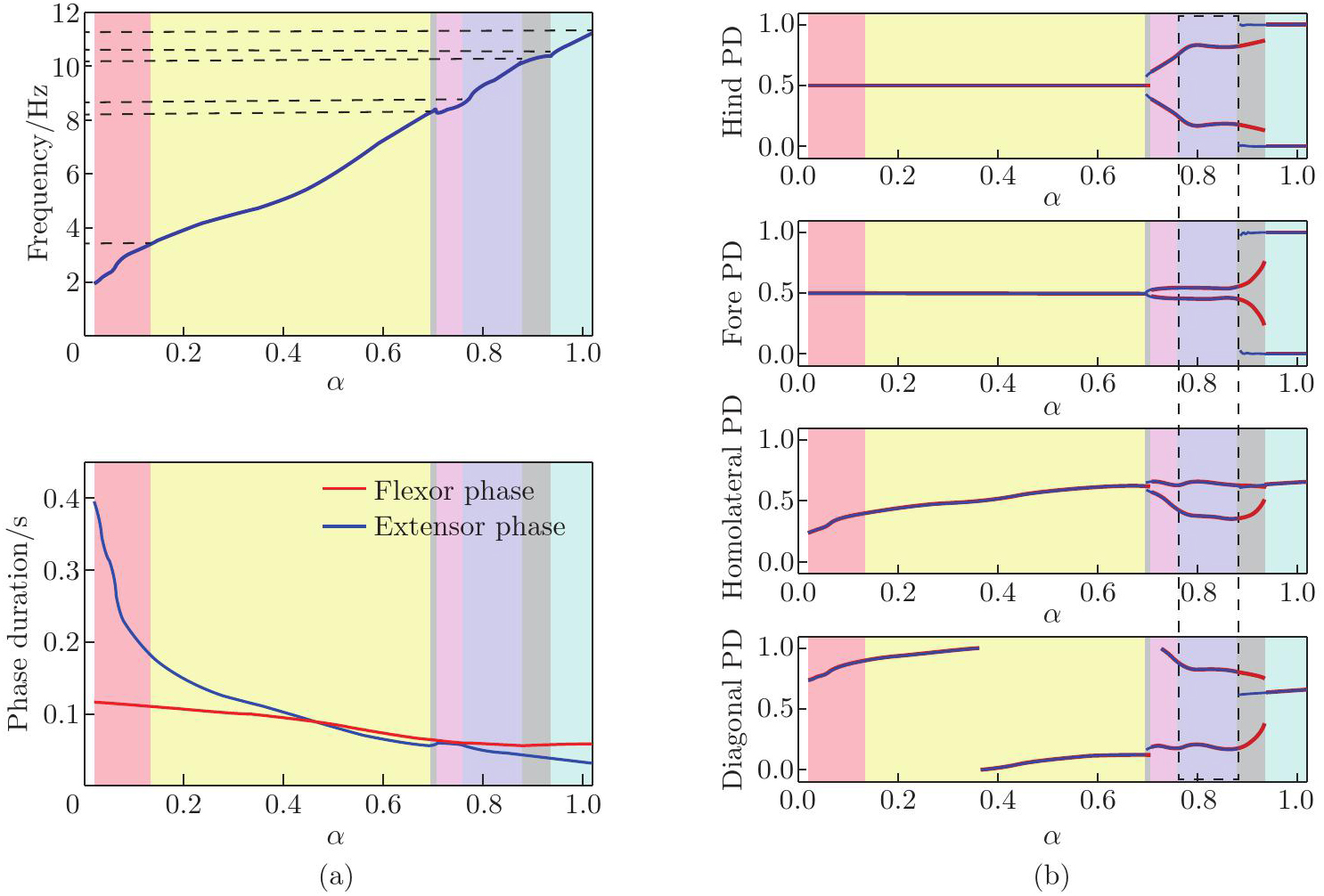
Fig. 4
(a)–(b) Gallop gait and the corresponding PD performances of the model (α=0.8). In (a), the top panel: activity of four flexor centers; the bottom panel: corresponding extension phases of four flexor centers. In (b), the activity of the left hind F/limb (black dot) is referenced. Red, green, and blue arrows represent the PDs of left-right hindlimbs, homolateral limbs, and diagonal limbs, respectively. (c) The PDs of left-right forelimbs corresponding to the four gaits. Blue, red, and black arrows represent the PDs of left-right forelimbs in walk (α=0.1)/trot (α=0.36), gallop α=0.8, and bound (α=1.0), respectively. F: flexor centers; lHl: left hindlimb; rHl: right hindlimb; lFl: left forelimb; rFl: right forelimb (color online)"
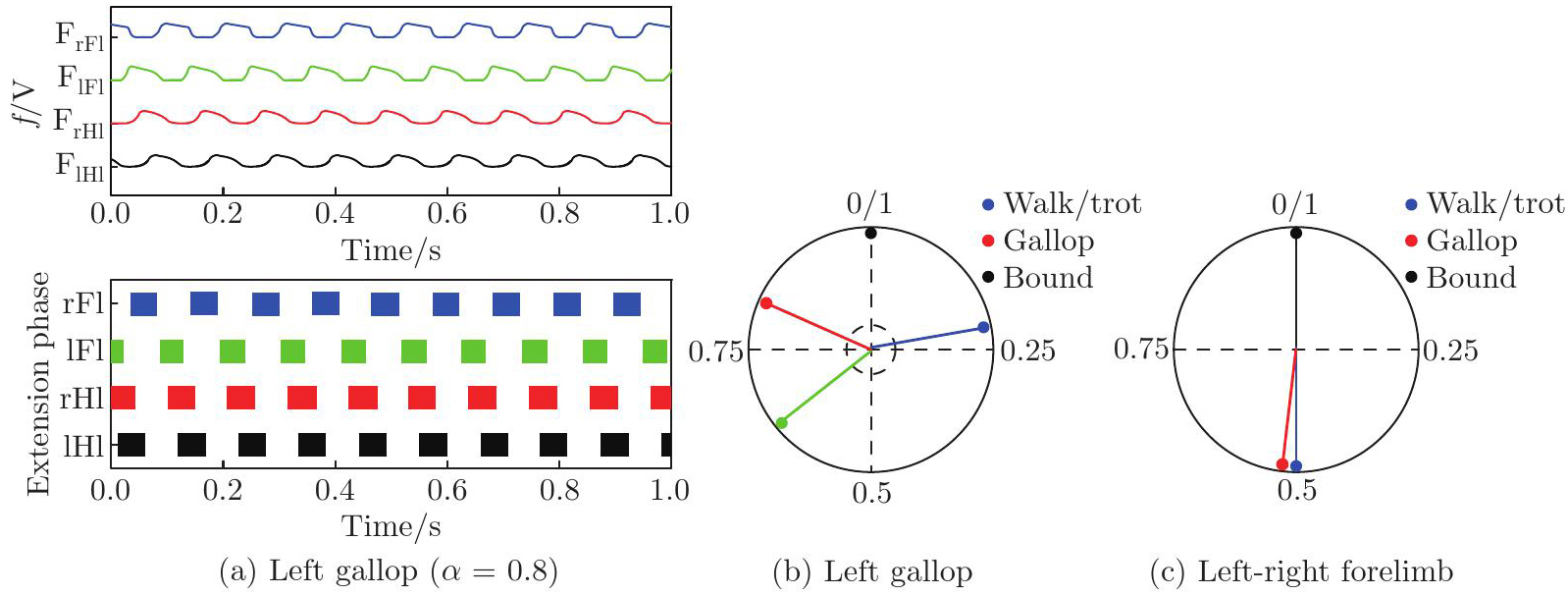
Fig. 5
Performance of the model regulated by IM. From top to bottom: locomotor frequency (the top panel), phase duration (the second panel), and PDs (the bottom six panels) as functions of gM. From left to right: α=0.03 (the left panel), α=0.15 (the middle panel), and α=0.5 (the right panel). Color related notes are the same as in Fig. 3 (color online)"
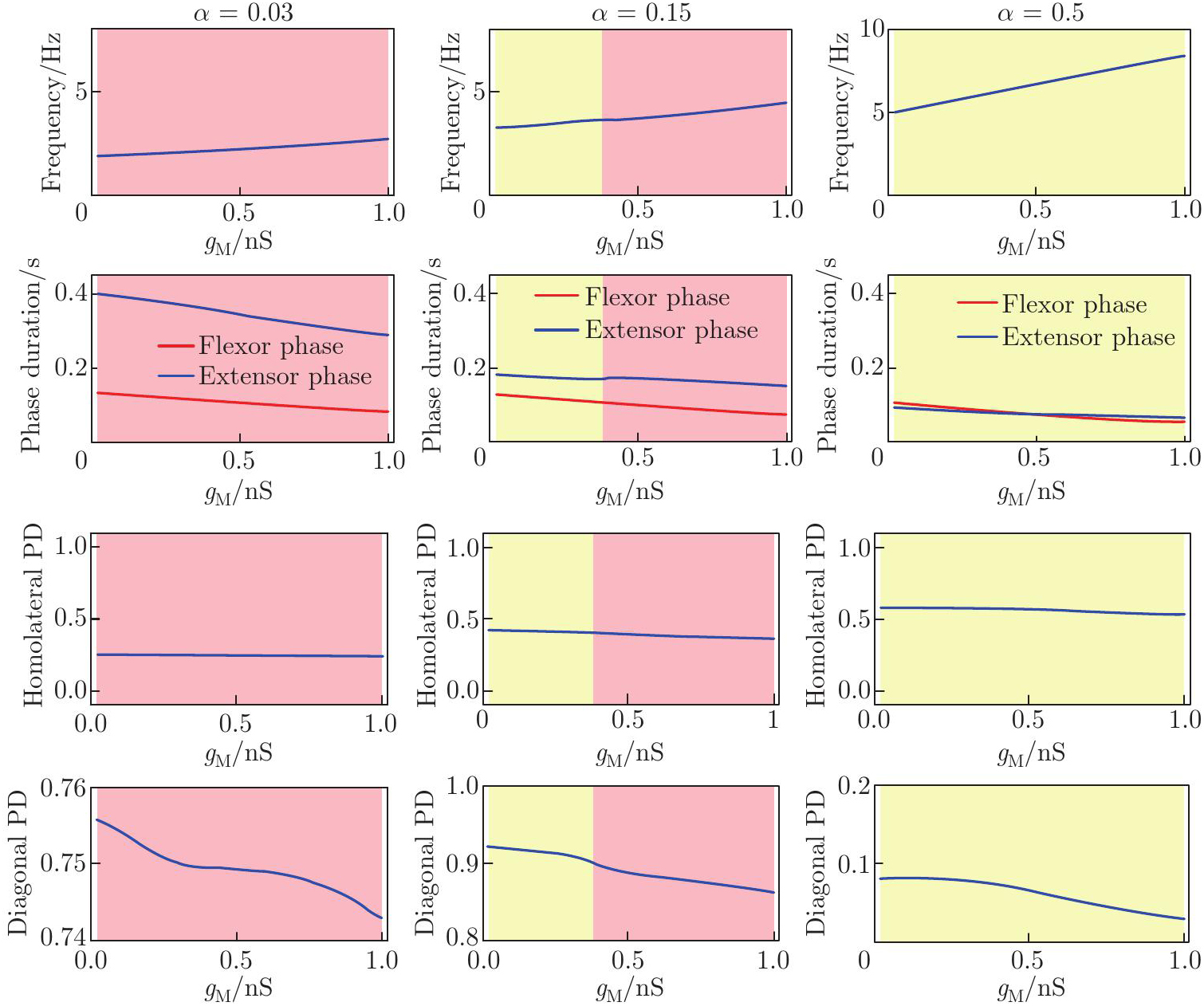
Fig. 6
Performance of the model regulated by INaP. From top to bottom: locomotor frequency (the top panel), phase duration (the second panel), and PDs (the bottom six panels) as functions of gNaP. From left to right: α=0.03 (the left panel), α=0.15 (the middle panel), and α=0.5 (the right panel). Color related notes are the same as in Fig. 3 (color online)"
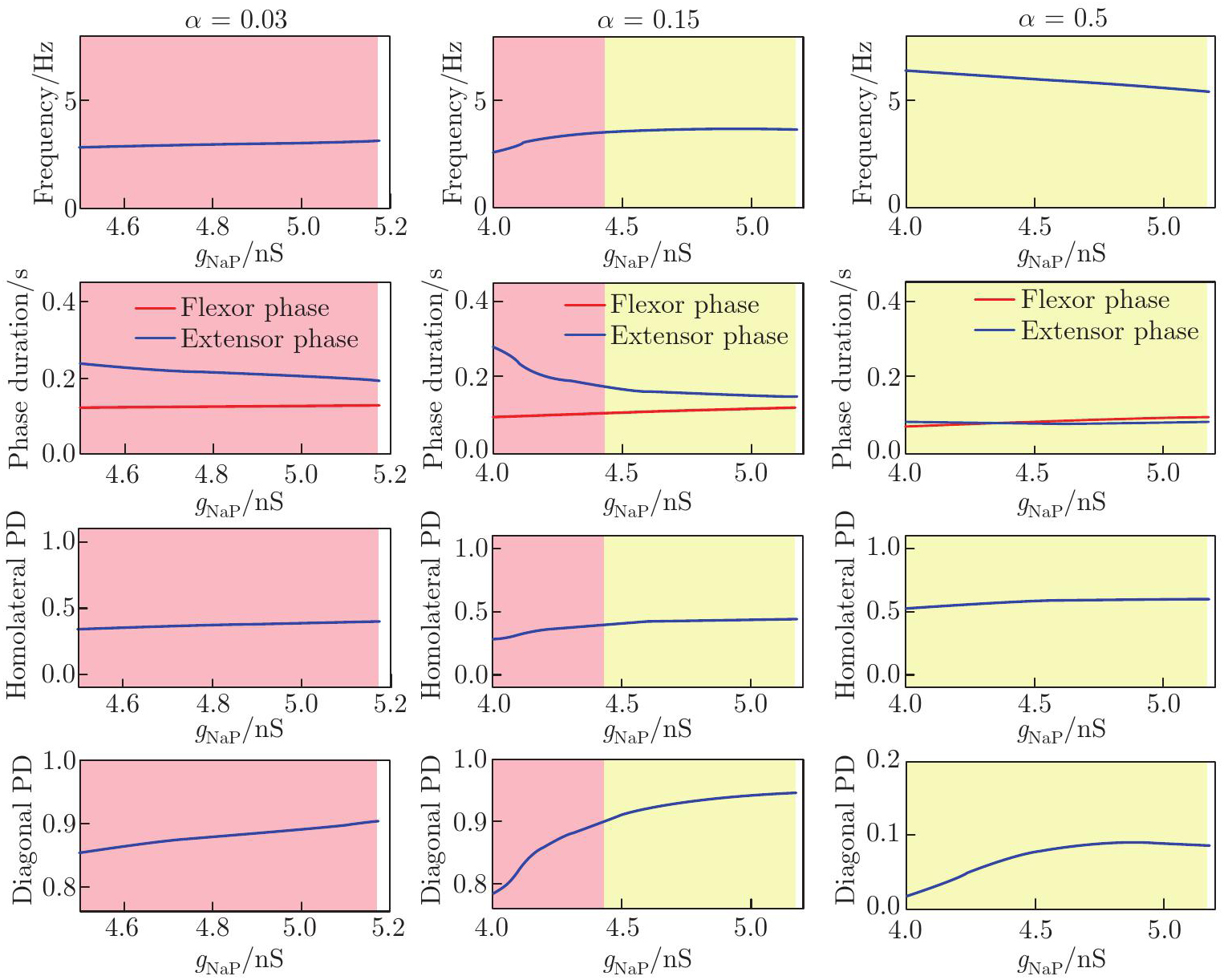

Fig. 8
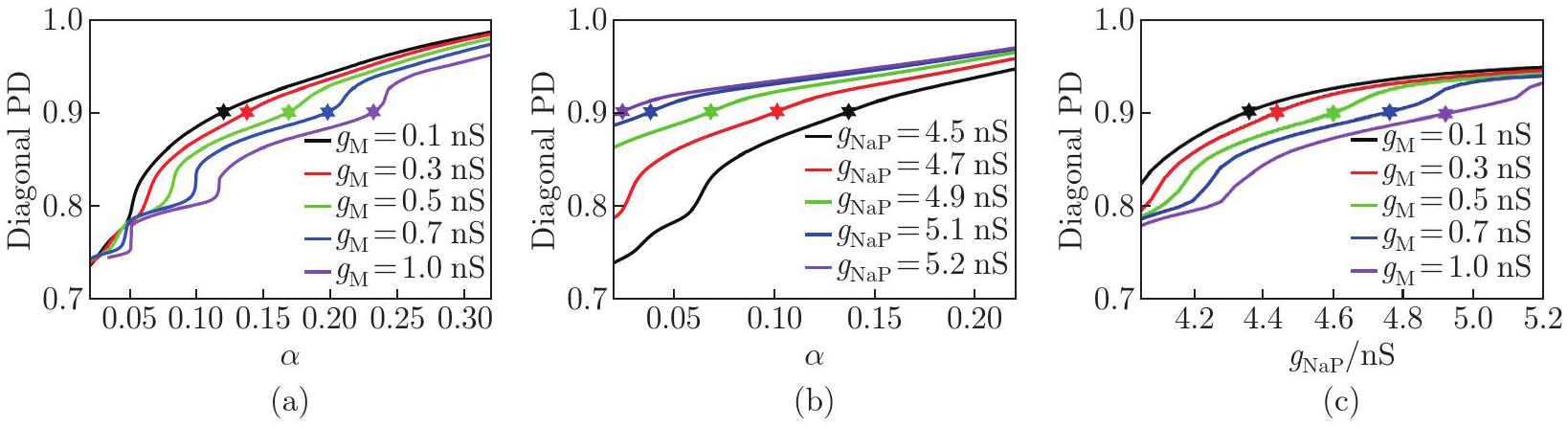
Interaction mechanisms between the brainstem drive and ionic currents in regulating locomotor gaits: diagonal PD as functions of α at different (a) gM and (b) gNaP, and (c) diagonal PD as functions of gNaP at different gM. The asterisks indicate the values of α or gNaP corresponding to the transition points at which the gait transitions from walk to trot (color online)"
| [1] | BATKA, R. J., BROWN, T. J., MCMILLAN, K. P., MEADOWS, R. M., JONES, K. J., and HAULCOMB, M. M. The need for speed in rodent locomotion analyses. Anatomical Record, 297(10), 1839–1864 (2014) |
| [2] | BELLARDITA, C. and KIEHN, O. Phenotypic characterization of speed-associated gait changes in mice reveals modular organization of locomotor networks. Current Biology, 25(11), 1426–1436 (2015) |
| [3] | LEIRAS, R., CREGG, J. M., and KIEHN, O. Brainstem circuits for locomotion. Annual Review of Neuroscience, 45, 63–85 (2022) |
| [4] | BROCARD, F. New channel lineup in spinal circuits governing locomotion. Current Opinion in Physiology, 8, 14–22 (2019) |
| [5] | GRILLNER, S. and EL MANIRA, A. Current principles of motor control, with special reference to vertebrate locomotion. Physiological Reviews, 100, 271–320 (2020) |
| [6] | WILSON, A. C. and SWEENEY, L. B. Spinal cords: symphonies of interneurons across species. Frontiers in Neural Circuits, 17, 1146449 (2023) |
| [7] | CAGGIANO, V., LEIRAS, R., GOÑI-ERRO, H., MASINI, D., BELLARDITA, C., BOUVIER, J., CALDEIRA, V., FISONE, G., and KIEHN, O. Midbrain circuits that set locomotor speed and gait selection. nature, 553(7689), 455–460 (2018) |
| [8] | JOSSET, N., ROUSSEL, M., LEMIEUX, M., LAFRANCE-ZOUBGA, D., RASTQAR, A., and BRETZNER, F. Distinct contributions of mesencephalic locomotor region nuclei to locomotor control in the freely behaving mouse. Current Biology, 28(6), 884–901 (2018) |
| [9] | VERNEUIL, J., BROCARD, C., TROUPLIN, V., VILLARD, L., PEYRONNET-ROUX, J., and BROCARD, F. The M-current works in tandem with the persistent sodium current to set the speed of locomotion. PLoS Biology, 18(1), e3000738 (2020) |
| [10] | DROUILLAS, B., BROCARD, C., ZANELLA, S., BOS, R., and BROCARD, F. Persistent Nav1.1 and Nav1.6 currents drive spinal locomotor functions through nonlinear dynamics. Cell Reports, 42, 113085 (2023) |
| [11] | SVENSSON, E., WILLIAMS, M. J., and SCHIÖTH, H. B. Neural cotransmission in spinal circuits governing locomotion. Trends in Neurosciences, 41(8), 540–555 (2018) |
| [12] | CÔTÉ, M. P., MURRAY, L. M., and KNIKOU, M. Spinal control of locomotion: individual neurons, their circuits and functions. Frontiers in Physiology, 9, 784 (2018) |
| [13] | HAQUE, F. and GOSGNACH, S. Mapping connectivity amongst interneuronal components of the locomotor CPG. Frontiers in Cellular Neuroscience, 13, 443 (2019) |
| [14] | TALPALAR, A. E., BOUVIER, J., BORGIUS, L., FORTIN, G., PIERANI, A., and KIEHN, O. Dual-mode operation of neuronal networks involved in left-right alternation. nature, 500(7460), 85–88 (2013) |
| [15] | KIEHN, O. Decoding the organization of spinal circuits that control locomotion. Nature Reviews Neuroscience, 17(4), 224–238 (2016) |
| [16] | GRILLNER, S. and KOZLOV, A. The CPGs for limbed locomotion-facts and fiction. International Journal of Molecular Sciences, 22(11), 5882 (2021) |
| [17] | FRIGON, A. The neural control of interlimb coordination during mammalian locomotion. Journal of Neurophysiology, 117(6), 2224–2241 (2017) |
| [18] | RUDER, L., TAKEOKA, A., and ARBER, S. Long-distance descending spinal neurons ensure quadrupedal locomotor stability. Neuron, 92(5), 1063–1078 (2016) |
| [19] | POCRATSKY, A. M., SHEPARD, C. T., MOREHOUSE, J. R., BURKE, D. A., RIEGLER, A. S., HARDIN, J. T., BEARE, J. E., HAINLINE, C., STATES, G. J., BROWN, B. L., WHITTEMORE, S. R., and MAGNUSON, D. S. Long ascending propriospinal neurons provide flexible, context-specific control of interlimb coordination. eLife, 9, e53565 (2020) |
| [20] | ZHANG, J., LANUZA, G. M., BRITZ, O., WANG, Z., SIEMBAB, V. C., ZHANG, Y., VELASQUEZ, T., ALVAREZ, F. J., FRANK, E., and GOULDING, M. V1 and V2b interneurons secure the alternating flexor-extensor motor activity mice require for limbed locomotion. Neuron, 82(1), 138–150 (2014) |
| [21] | CABELGUEN, J. M., ORSAL, D., PERRET, C., and ZATTARA, M. Central pattern generation of forelimb and hindlimb locomotor activities in the cat. Advances in Physiology Education, 1, 199–211 (1980) |
| [22] | HAYASHI, M., HINCKLEY, C. A., DRISCOLL, S. P., MOORE, N. J., LEVINE, A. J., HILDE, K. L., SHARMA, K., and PFAFF, S. L. Graded arrays of spinal and supraspinal V2a interneuron subtypes underlie forelimb and hindlimb motor control. Neuron, 97(4), 869–884 (2018) |
| [23] | CRONE, S. A., ZHONG, G., HARRIS-WARRICK, R., and SHARMA, K. In mice lacking V2a interneurons, gait depends on speed of locomotion. The Journal of Neuroscience, 29(21), 7098–7109 (2009) |
| [24] | AZIM, E., JIANG, J., ALSTERMARK, B., and JESSELL, T. M. Skilled reaching relies on a V2a propriospinal internal copy circuit. nature, 508(7496), 357–363 (2014) |
| [25] | ZELENIN, P. V., VEMULA, M. G., LYALKA, V. F., KIEHN, O., TALPALAR, A. E., and DELIAGINA, T. G. Differential contribution of V0 interneurons to execution of rhythmic and nonrhythmic motor behaviors. The Journal of Neuroscience, 41(15), 3432–3445 (2021) |
| [26] | DANNER, S. M., WILSHIN, S. D., SHEVTSOVA, N. A., and RYBAK, I. A. Central control of interlimb coordination and speed-dependent gait expression in quadrupeds. Journal of Physiology, 594(23), 6947–6967 (2016) |
| [27] | DANNER, S. M., SHEVTSOVA, N. A., FRIGON, A., and RYBAK, I. A. Computational modeling of spinal circuits controlling limb coordination and gaits in quadrupeds. eLife, 6, e31050 (2017) |
| [28] | AUSBORN, J., SHEVTSOVA, N. A., CAGGIANO, V., DANNER, S. M., and RYBAK, I. A. Computational modeling of brainstem circuits controlling locomotor frequency and gait. eLife, 8, e43587 (2019) |
| [29] | LEMIEUX, M., JOSSET, N., ROUSSEL, M., COURAUD, S., and BRETZNER, F. Speed-dependent modulation of the locomotor behavior in adult mice reveals attractor and transitional gaits. Frontiers in Neuroscience, 10, 42 (2016) |
| [30] | ZHU, Q., WANG, F., and HAN, F. Contributions of M- and persistent sodium currents in regulating locomotor rhythms: a computational modeling study. International Journal of Bifurcation and Chaos, 33(12), 2350143 (2023) |
| [31] | ZHU, Q., HAN, F., YU, Y., WANG, F., WANG, Q., and SHAKEEL, A. A spinal circuit model with asymmetric cervical-lumbar layout controls backward locomotion and scratching in quadrupeds. Neural Networks, 178, 106422 (2024) |
| [32] | SHEVTSOVA, N. A., LI, E. Z., SINGH, S., DOUGHERTY, K. J., and RYBAK, I. A Ipsilateral and contralateral interactions in spinal locomotor circuits mediated by V1 neurons: insights from computational modeling. International Journal of Molecular Sciences, 23, 5541 (2022) |
| [33] | ZHONG, G., SHEVTSOVA, N. A., RYBAK, I. A., and HARRIS-WARRICK, R. M. Neuronal activity in the isolated mouse spinal cord during spontaneous deletions in fictive locomotion: insights into locomotor central pattern generator organization. The Journal of Physiology, 590(19), 4735–4759 (2012) |
| [34] | MACHADO, T. A., PNEVMATIKAKIS, E., PANINSKI, L., JESSELL, T. M., and MIRI, A. Primacy of flexor locomotor pattern revealed by ancestral reversion of motor neuron identity. Cell, 162(2), 338–350 (2015) |
| [35] | YANG, L., SINGLA, D., WU, A. K., CROSS, K. A., and MASMANIDIS, S. C. Dopamine lesions alter the striatal encoding of single-limb gait. eLife, 12, RP92821 (2023) |
| [36] | FAN, D., ZHENG, Y., YANG, Z., and WANG, Q. Improving control effects of absence seizures using single-pulse alternately resetting stimulation (SARS) of corticothalamic circuit. Applied Mathematics and Mechanics (English Edition), 41(9), 1287–1302 (2020) https://doi.org/10.1007/s10483-020-2644-8 |
| [37] | ZHU, Q., HAN, F., YUAN, Y., and SHEN, L. A TAN-dopamine interaction mechanism based computational model of basal Ganglia in action selection. Cognitive Neurodynamics, 18, 2127–2144 (2024) |
| [38] | MAO, X. and LEI, F. Stability analysis and coexisting behaviors of a delayed multiplex network under electromagnetic radiation. International Journal of Bifurcation and Chaos, 32(10), 2250148 (2022) |
| [39] | MA, J., QIN, H., SONG, X., and CHU, R. T. Pattern selection in neuronal network driven by electric autapses with diversity in time delays. International Journal of Modern Physics B, 29(1), 1450239 (2015) |
| [40] | JI, Y. and MAO, X. Fast and slow dynamical behaviors of delayed-coupled thermosensitive neurons under electromagnetic induction. Chaos Solitons & Fractals, 189, 115721 (2024) |
| [41] | LEI, Z. and MA, J. Coherence resonance and energy dynamics in a memristive map neuron. Chaos, 35(2), 023158 (2025) |
| [42] | MAO, X., LI, X., DING, W., WANG, S., ZHOU, X., and QIAO, L. Dynamics of a multiplex neural network with delayed couplings. Applied Mathematics and Mechanics (English Edition), 42(3), 441–456 (2021) https://doi.org/10.1007/s10483-021-2709-6 |
| [1] | Wei WANG, Rubin WANG. Control strategy of central pattern generator gait movement under condition of attention selection [J]. Applied Mathematics and Mechanics (English Edition), 2016, 37(7): 957-966. |
| [2] | DONG Wei;WANG Ru-Bin;ZHANG Zhi-Kang. Exploring human rhythmic gait movement in the role of cerebral cortex signal [J]. Applied Mathematics and Mechanics (English Edition), 2011, 2(32): 223-230. |
| Viewed | ||||||
|
Full text |
|
|||||
|
Abstract |
|
|||||


 Email Alert
Email Alert RSS
RSS