Fig. 1

The LCE self-oscillating system consisting of a thermally-responsive LCE fiber and a mass under a linear temperature field. (a) The reference state; (b) the current state; (c) the force analysis of the mass (color online)"

Table 1

Material properties and geometric parameters"

Table 2

Dimensionless parameters"

Fig. 2

Self-oscillation of the LCE fiber-mass system. The parameters are ${\bar K}$=12, α=-0.38, β=1, ${\bar a}$1=0.06, and τ=0.01. (a) and (b) the static regime for ${\bar a}$0=0.1; (c) and (d) the self-oscillation regime for ${\bar a}$0=0.01 (color online)"

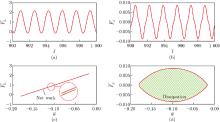
Fig. 3

Self-oscillation mechanism of the system. (a) The time history curve of the driving force for ${\bar a}$0=0.01; (b) the time history curve of the damping force for ${\bar a}$0=0.01; (c) the dependence of the driving force on mass displacement for ${\bar a}$0=0.01; (d) the dependence of the damping force on mass displacement for ${\bar a}$0=0.01 (color online)"

Fig. 4

Effects of the elastic coefficient of the liquid crystal elastomer on the amplitude, frequency, and ε. The parameters are α=-0.38, β=1, ${\bar a}$0 =0.01, ${\bar a}$1 =0.06, and τ=0.01. (a) Effects of the elastic coefficient of the liquid crystal elastomer on the amplitude and ε; (b) effects of the elastic coefficient of the liquid crystal elastomer on the frequency and ε (color online)"

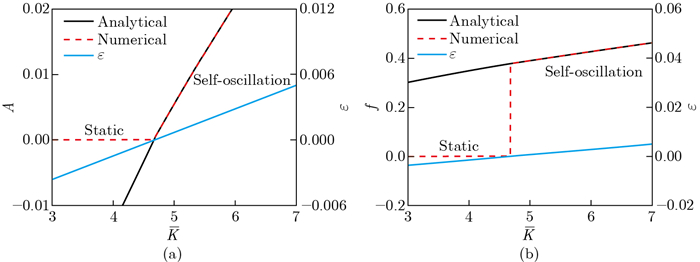
Fig. 5

Effects of the thermal expansion coefficient on the amplitude and frequency with the system parameters of ${\bar K}$=12, β=1, ${\bar a}$0=0.01, ${\bar a}$1=0.06, and τ=0.01. (a) Effects of the thermal expansion coefficient on the amplitude and ε; (b) effects of the thermal expansion coefficient on the frequency and ε (color online)"

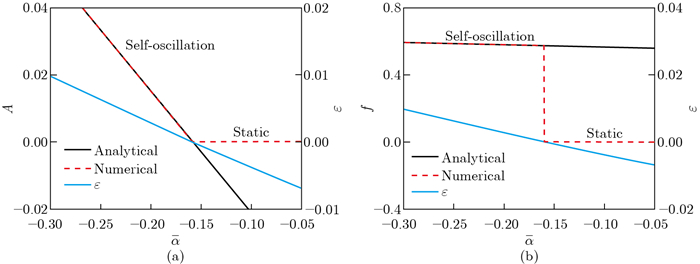
Fig. 6

Effects of the temperature gradient on the amplitude, frequency and ε. The parameters are ${\bar K}$=12, α=-0.38, ${\bar a}$0 =0.01, ${\bar a}$1=0.06, and τ=0.01. (a) Effects of the temperature gradient on the amplitude and ε; (b) effects of the temperature gradient on the frequency and ε (color online)"

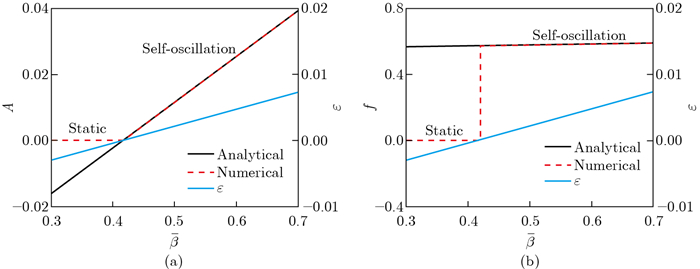
Fig. 7

Effects of the first damping coefficient on the amplitude, frequency, and ε. The parameters are ${\bar K}$=12, α=-0.38, β=1, ${\bar a}$1=0.06, and τ=0.01. (a) Effects of the first damping coefficient on the amplitude and ε; (b) effects of the first damping coefficient on the frequency and ε (color online)"

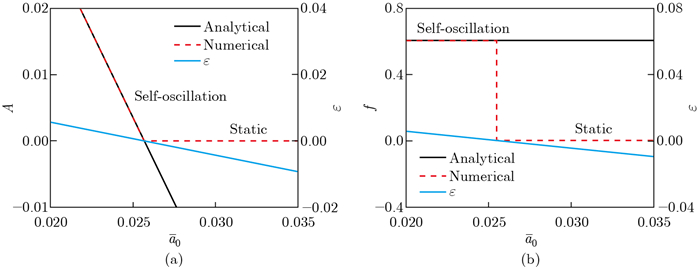
Fig. 8

Effects of the second damping coefficient on the amplitude, frequency, and ε. The parameters are ${\bar K}$=12, α=-0.38, β=1, ${\bar a}$0 =0.01, and τ=0.01. (a) Effects of the second damping coefficient on the amplitude and ε; (b) effects of the second damping coefficient on the frequency and ε (color online)"

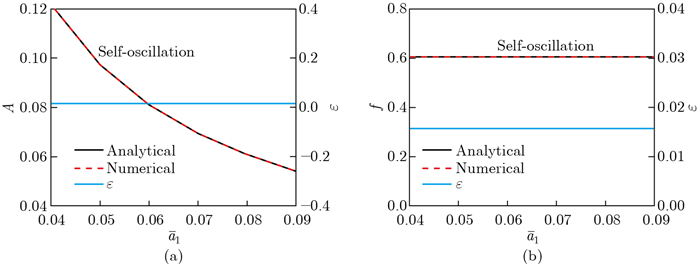
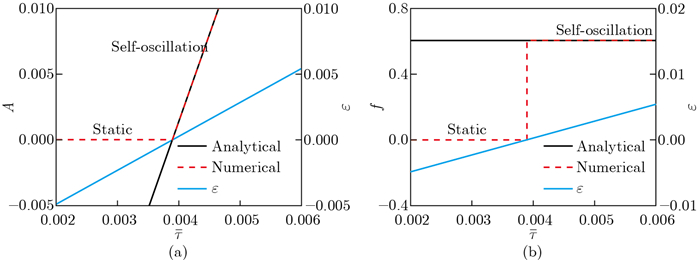
Fig. 9

Effects of the characteristic time on the amplitude, frequency, and ε. The parameters are ${\bar K}$=12, α=-0.38, β=1, ${\bar a}$0=0.01, and ${\bar a}$1=0.06. (a) Effects of the characteristic time on the amplitude and ε; (b) effects of the characteristic time on the frequency and ε (color online)"

Table 3

Effects of parameters on the amplitude and frequency"