Applied Mathematics and Mechanics (English Edition) ›› 2024, Vol. 45 ›› Issue (2): 239-260.doi: https://doi.org/10.1007/s10483-024-3083-6
• Articles • Previous Articles Next Articles
Jie JING1, Xiaoye MAO1,2,*(
), Hu DING1,2, Liqun CHEN1,2
Email Alert
RSSReceived:2023-10-07
Online:2024-02-01
Published:2024-01-27
Contact:
Xiaoye MAO
E-mail:xmao3@shu.edu.cn
Supported by:2010 MSC Number:
Jie JING, Xiaoye MAO, Hu DING, Liqun CHEN. Parametric resonance of axially functionally graded pipes conveying pulsating fluid. Applied Mathematics and Mechanics (English Edition), 2024, 45(2): 239-260.
Fig. 1
Model of the AFG pipe conveying fluid (color online)"
Table 1
Comparison of values before and after buckling (Γ0-sup = 1.1Γ0-cr)"
 |
Fig. 2
Parametric resonance boundaries in the subcritical region: (a) pulsating flow velocity boundaries; (b) damping boundaries (color online)"
Fig. 3
Total responses of parametric resonance at the midpoint of the subcritical pipe: (a) time history via the DQEM; (b) numerical and analytical solutions (color online)"
Fig. 4
(a) Pulsating flow velocity boundary under different αE. Total responses of the pipe under different pulsating flow velocities at (b) αE=0.8, (c) αE=1.0, and (d)αE=1.2 (color online)"
Fig. 5
Responses of the subcritical pipe at 0.25L and 0.75L under (a) αE=0.4, 0.8 and (b) αE=1.2, 1.6 (color online)"
Fig. 6
Relative deviations of the non-trivial response at 0.25L and 0.75L of the subcritical pipe: (a) stable solution; (b) unstable solution (color online)"
Fig. 7
Parametric resonance boundaries in the supercritical region: (a) pulsating flow velocity boundaries; (b) damping boundaries (color online)"
Fig. 8
Time history of the supercritical pipe via the DQEM (color online)"
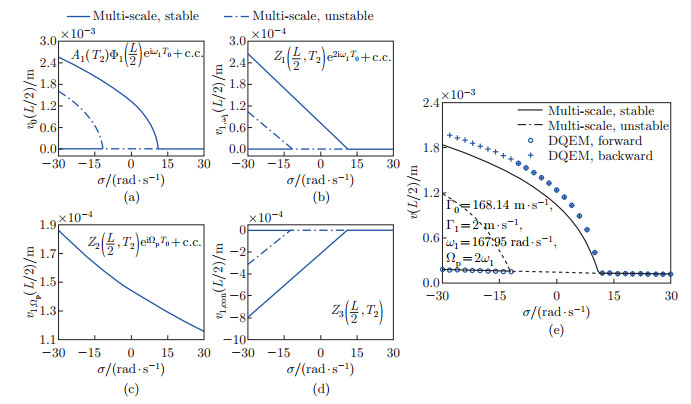
Fig. 9
Analyses of (a) the solution of the midpoint at the T0 scale, (b) the natural frequency component of the midpoint at the T1 scale, (c) the external excitation frequency component of the midpoint at the T1 scale, (d) the zero-shift component of the midpoint at the T1 scale, and (e) the synthesis of the T0 and T1 scale solutions (color online)"
Fig. 10
(a) Pulsating flow velocity boundaries at different αE. Total responses at (b) αE=0.8, (c)αE=1.2, and (d) αE=1.4 (color online)"
Fig. 11
Responses of the supercritical pipe at 0.25L and 0.75L under (a) αE=0.4, 0.8 and (b) αE=1.2, 1.4 (color online)"
Fig. 12
Relative deviations of the parametric response at 0.25L and 0.75L of the supercritical pipe: (a) stable solution; (b) unstable solution (color online)"
Table 2
Comparison of parametric vibration in the subcritical and supercritical regions (Γ0-sup = 1.1Γ0-cr)"
 |
Fig. 13
Pulsating flow velocity boundaries of the pipe at (a)αE=0.4 and (c) αE=1.4. (b) Relationship between the gradient parameter and the pulsating flow velocity boundaries (color online)"
Fig. 14
Damping boundaries of the pipe at (a) αE=0.4 and (c) αE=1.4. (b) Relationship between the gradient parameter and the damping boundaries (color online)"
Fig. 15
Parametric responses at (a) αE=0.4, (b)αE=0.8, (c)αE=1.2, and (d) αE=1.4 before and after buckling (color online)"
| 1 | IBRAHIM,R. A.Overview of mechanics of pipes conveying fluids — part I: fundamental studies.Journal of Pressure Vessel Technology,132,034001(2010) |
| 2 | ALI,H. H.,MUSTAFA,A. W., andAL-BAKRI,F. F.A new control design and robustness analysis of a variable speed hydrostatic transmission used to control the velocity of a hydraulic cylinder.International Journal of Dynamics and Control,9(3),1078-1091(2020) |
| 3 | GAO,P. X.,YU,T.,ZHANG,Y. L.,WANG,J., andZHAI,J. Y.Vibration analysis and control technologies of hydraulic pipeline system in aircraft: a review.Chinese Journal of Aeronautics,34(4),83-114(2021) |
| 4 | GUO,X. M.,CAO,Y. M.,MA,H.,XIAO,C. L., andWEN,B. C.Dynamic analysis of an L-shaped liquid-filled pipe with interval uncertainty.International Journal of Mechanical Sciences,217,107040(2022) |
| 5 | LI,M.,XU,Q.,CHEN,X. C.,ZHANG,X. L., andLI,Y. H.Modeling and modal analysis of non-uniform multi-span oil-conveying pipes with elastic foundations and attachments.Applied Mathematical Modelling,88,661-675(2020) |
| 6 | LIANG,F.,GAO,A.,LI,X. F., andZHU,W. D.Nonlinear parametric vibration of spinning pipes conveying fluid with varying spinning speed and flow velocity.Applied Mathematical Modelling,95,320-338(2021) |
| 7 | PAÏDOUSSIS,M. P., andISSID,N. T.Dynamic stability of pipes conveying fluid.Journal of Sound and Vibration,33(3),267-294(1974) |
| 8 | PLAUT,R. H., andHUSEYIN,K.Instability of fluid conveying pipes under axial load.Journal of Applied Mechanics,42(4),889-890(1975) |
| 9 | MATSUZAKI,Y., andFUNG,Y. C.Nonlinear stability analysis of a two-dimensional model of an elastic tube conveying a compressible flow.Journal of Applied Mechanics,46(1),31-36(1979) |
| 10 | PANDA,L. N., andKAR,R. C.Nonlinear dynamics of a pipe conveying pulsating fluid with combination, principal parametric and internal resonances.Journal of Sound and Vibration,309(3-5),375-406(2008) |
| 11 | BURAK-ÖZHAN,B., andPAKDEMIRLI,M.Principal parametric resonances of a general continuous system with cubic nonlinearities.Applied Mathematics and Computation,219(5),2412-2423(2012) |
| 12 | ZHU,B.,GUO,Y.,ZHAO,T., andLI,X.Nonlinear dynamics of inclined viscoelastic pipes subjected to pulsatile flow and multi-harmonic excitations.Nonlinear Dynamics,111(13),11823-11849(2023) |
| 13 | SHAIK,N. H.,SHARMA,A. K., andBHATTACHARYA,B.Effect of shape memory alloy actuation on parametric instability in pipes conveying pulsating fluid.Journal of Vibration Engineering & Technologies,11,3003-3016(2023) |
| 14 | WEI,S.,YAN,X.,LI,X.,DING,H., andCHEN,L. Q.Parametric vibration of a nonlinearly supported pipe conveying pulsating fluid.Nonlinear Dynamics,111(18),16643-16661(2023) |
| 15 | GUO,X. M.,GAO,P. X.,MA,H.,LI,H.,WANG,B.,HAN,Q. K., andWEN,B. C.Vibration characteristics analysis of fluid-conveying pipes concurrently subjected to base excitation and pulsation excitation.Mechanical Systems and Signal Processing,189,110086(2023) |
| 16 | WANG,Y. K.,TANG,M.,YANG,M., andQIN,T.Three-dimensional dynamics of a cantilevered pipe conveying pulsating fluid.Applied Mathematical Modelling,114,502-524(2023) |
| 17 | GUO,Y.,ZHU,B., andLI,Y. H.Nonlinear dynamics of fluid-conveying composite pipes subjected to time-varying axial tension in sub- and super-critical regimes.Applied Mathematical Modelling,101,632-653(2022) |
| 18 | ZHU,B.,ZHANG,X., andZHAO,T.Nonlinear planar and non-planar vibrations of viscoelastic fluid-conveying pipes with external and internal resonances.Journal of Sound and Vibration,548,117558(2023) |
| 19 | XIE,W. D.,LIANG,Z. L.,JIANG,Z. Y., andZHU,L. X.Dynamic responses of a flexible pipe conveying variable-density fluid and experiencing cross-flow and in-line coupled vortex-induced vibrations.Ocean Engineering,260,111811(2022) |
| 20 | GHADIRIAN,H.,MOHEBPOUR,S.,MALEKZADEH,P., andDANESHMAND,F.Nonlinear free vibrations and stability analysis of FG-CNTRC pipes conveying fluid based on Timoshenko model.Composite Structures,292,115637(2022) |
| 21 | XU,W. H.,JIA,K.,MA,Y. X.,WANG,Y. Y., andSONG,Z. Y.Multispan classification methods and interaction mechanism of submarine pipelines undergoing vortex-induced vibration.Applied Ocean Research,120,103027(2022) |
| 22 | LI,M. W.,YAN,H., andWANG,L.Nonlinear model reduction for a cantilevered pipe conveying fluid: a system with asymmetric damping and stiffness matrices.Mechanical Systems and Signal Processing,188,109993(2023) |
| 23 | DING,H.,JI,J. C., andCHEN,L. Q.Nonlinear vibration isolation for fluid-conveying pipes using quasi-zero stiffness characteristics.Mechanical Systems and Signal Processing,121,675-688(2019) |
| 24 |
WEI,S.,YAN,X.,FAN,X.,MAO,X. Y.,DING,H., andCHEN,L. Q.Vibration of fluid-conveying pipe with nonlinear supports at both ends.Applied Mathematics and Mechanics (English Edition),43(6),845-862(2022)
doi: 10.1007/s10483-022-2857-6 |
| 25 | ZHOU,K.,YI,H. R.,DAI,H. L.,YAN,H.,GUO,Z. L.,XIONG,F. R.,NI,Q.,HAGEDORN,P., andWANG,L.Nonlinear analysis of L-shaped pipe conveying fluid with the aid of absolute nodal coordinate formulation.Nonlinear Dynamics,107(1),391-412(2021) |
| 26 | CHEN,F. J.,CHEN,J. Y.,DUAN,R. Q.,HABIBI,M., andKHADIMALLAH,M. A.Investigation on dynamic stability and aeroelastic characteristics of composite curved pipes with any yawed angle.Composite Structures,284,115195(2022) |
| 27 | MAKNUN,I. J.,NATARAJAN,S., andKATILI,I.Application of discrete shear quadrilateral element for static bending, free vibration and buckling analysis of functionally graded material plate.Composite Structures,284,115130(2022) |
| 28 | CHANDRASEKARAN,S.,HARI,S., andAMIRTHALINGAM,M.Functionally graded materials for marine risers by additive manufacturing for high-temperature applications: experimental investigations.Structures,35,931-938(2022) |
| 29 | ZHEN,Y. X.,GONG,Y. F., andTANG,Y.Nonlinear vibration analysis of a supercritical fluid-conveying pipe made of functionally graded material with initial curvature.Composite Structures,268,113980(2021) |
| 30 | ZHU,B.,GUO,Y.,CHEN,B., andLI,Y. H.Nonlinear nonplanar dynamics of porous functionally graded pipes conveying fluid.Communications in Nonlinear Science and Numerical Simulation,117,106907(2023) |
| 31 | SELMI,A., andHASSIS,H.Vibration analysis of post-buckled fluid-conveying functionally graded pipe.Composites Part C: Open Access,4,100117(2021) |
| 32 | JIN,Q.,REN,Y., andYUAN,F. G.Combined resonance of pulsatile flow-transporting FG nanotubes under forced excitation with movable boundary.Nonlinear Dynamics,111(7),6157-6178(2022) |
| 33 | DING,H. X.,SHE,G. L., andZHANG,Y. W.Nonlinear buckling and resonances of functionally graded fluid-conveying pipes with initial geometric imperfection.The European Physical Journal Plus,137(12),1329(2022) |
| 34 | GUO,X. M.,XIAO,C. L.,GE,H.,MA,H.,LI,H.,SUN,W., andLIU,Z. H.Dynamic modeling and experimental study of a complex fluid-conveying pipeline system with series and parallel structures.Applied Mathematical Modelling,109,186-208(2022) |
| 35 | ZHAO,Y.,FENG,J. M.,ZHAO,B.,ZHOU,S. M.,TANG,Z., andPENG,X. Y.Vibration analysis and control of a screw compressor outlet piping system.Proceedings of the Institution of Mechanical Engineers, Part E: Journal of Process Mechanical Engineering,233(2),403-411(2018) |
| 36 | DAI,J. Y.,LIU,Y. S.,LIU,H. C.,MIAO,C. X., andTONG,G. J.A parametric study on thermo-mechanical vibration of axially functionally graded material pipe conveying fluid.International Journal of Mechanics and Materials in Design,15(4),715-726(2019) |
| 37 | AN,C., andSU,J.Dynamic behavior of axially functionally graded pipes conveying fluid.Mathematical Problems in Engineering,2017,6789634(2017) |
| 38 | LU,Z. Q.,ZHANG,K. K.,DING,H., andCHEN,L. Q.Nonlinear vibration effects on the fatigue life of fluid-conveying pipes composed of axially functionally graded materials.Nonlinear Dynamics,100(2),1091-1104(2020) |
| 39 | GUO,Q.,LIU,Y. S.,CHEN,B. Q., andZHAO,Y. Z.An efficient stochastic natural frequency analysis method for axially varying functionally graded material pipe conveying fluid.European Journal of Mechanics-A/Solids,86,104155(2021) |
| 40 | TUO,Y. H.,FU,G. M.,SUN,B. J.,LOU,M., andSU,J.Stability of axially functionally graded pipe conveying fluid: generalized integral transform solution.Applied Ocean Research,125,103218(2022) |
| 41 | FAN,X.,WU,N.,LIU,Y., andGUO,Q.Resonance system reliability and sensitivity analysis method for axially FGM pipes conveying fluid with adaptive Kriging model.Acta Mechanica Solida Sinica,35(6),1021-1029(2022) |
| 42 | AGHAZADEH,R.Stability analysis of fluid conveying axially functionally graded micro-pipes using a refined tube model.Arabian Journal for Science and Engineering,47(7),8739-8750(2022) |
| 43 | AGHAZADEH,R.The effects of gravity and material gradation on the stability of axially functionally graded cantilevered pipes conveying fluid.Journal of the Chinese Society of Mechanical Engineers,43,153-164(2022) |
| 44 | FU,G.,TUO,Y.,ZHANG,H.,SU,J.,SUN,B.,WANG,K., andLOU,M.Effects of material characteristics on nonlinear dynamics of viscoelastic axially functionally graded material pipe conveying pulsating fluid.Journal of Marine Science and Application,22(2),247-259(2023) |
| 45 | BABILIO,E.Dynamics of functionally graded beams on viscoelastic foundation.International Journal of Structural Stability and Dynamics,14(8),1440014(2014) |
| 46 | MAO,X. Y.,JING,J.,DING,H., andCHEN,L. Q.Dynamics of axially functionally graded pipes conveying fluid.Nonlinear Dynamics,111(12),11023-11044(2023) |
| 47 | FAN,X.,ZHU,C. A.,MAO,X. Y., andDING,H.Resonance regulation on a hydraulic pipe via boundary excitations.International Journal of Mechanical Sciences,252,108375(2023) |
| 48 | CHEN,L. Q., andZU,J. W.Solvability condition in multi-scale analysis of gyroscopic continua.Journal of Sound and Vibration,309(1-2),338-342(2008) |
| 49 | WANG,X. W., andGU,H. Z.Static analysis of frame structures by the differential quadrature element method.International Journal for Numerical Methods in Engineering,40(4),759-772(1997) |
| 50 | SHU,C.,CHEW,Y. T., andRICHARDS,B. E.Generalized differential and integral quadrature and their application to solve boundary layer equations.International Journal for Numerical Methods in Fluids,21(9),723-733(1995) |
| 51 | DING,H.,YAN,Q. Y., andZU,J. W.Chaotic dynamics of an axially accelerating viscoelastic beam in the supercritical regime.International Journal of Bifurcation and Chaos,24(5),1450062(2014) |
| 52 | WANG,X. W., andWANG,Y. L.Free vibration analysis of multiple-stepped beams by the differential quadrature element method.Applied Mathematics and Computation,219(11),5802-5810(2013) |
| 53 | WANG,Y. L.,WANG,X. W., andZHOU,Y.Static and free vibration analyses of rectangular plates by the new version of the differential quadrature element method.International Journal for Numerical Methods in Engineering,59(9),1207-1226(2004) |
| [1] | Hanxiao GUO, Peifeng GAO, Xingzhe WANG. Integrated multi-scale approach combining global homogenization and local refinement for multi-field analysis of high-temperature superconducting composite magnets [J]. Applied Mathematics and Mechanics (English Edition), 2024, 45(5): 747-762. |
| [2] | Haiyang WU, Jiangfeng LOU, Biao ZHANG, Yuntong DAI, Kai LI. Stability analysis of a liquid crystal elastomer self-oscillator under a linear temperature field [J]. Applied Mathematics and Mechanics (English Edition), 2024, 45(2): 337-354. |
| [3] | Runqing CAO, Zilong GUO, Wei CHEN, Huliang DAI, Lin WANG. Nonlinear dynamics of a circular curved cantilevered pipe conveying pulsating fluid based on the geometrically exact model [J]. Applied Mathematics and Mechanics (English Edition), 2024, 45(2): 261-276. |
| [4] | Xin FAN, Changan ZHU, Xiaoye MAO, Hu DING. Adjacent mode resonance of a hydraulic pipe system consisting of parallel pipes coupled at middle points [J]. Applied Mathematics and Mechanics (English Edition), 2023, 44(3): 363-380. |
| [5] | Shaopeng WANG, Jun HONG, Dao WEI, Gongye ZHANG. Bending and wave propagation analysis of axially functionally graded beams based on a reformulated strain gradient elasticity theory [J]. Applied Mathematics and Mechanics (English Edition), 2023, 44(10): 1803-1820. |
| [6] | Zilong GUO, Qiao NI, Wei CHEN, Huliang DAI, Lin WANG. Dynamic analysis and regulation of the flexible pipe conveying fluid with a hard-magnetic soft segment [J]. Applied Mathematics and Mechanics (English Edition), 2022, 43(9): 1415-1430. |
| [7] | Huliang DAI, Yixiang HE, Kun ZHOU, Zerui PENG, Lin WANG, P. HAGEDORN. Utilization of nonlinear vibrations of soft pipe conveying fluid for driving underwater bio-inspired robot [J]. Applied Mathematics and Mechanics (English Edition), 2022, 43(7): 1109-1124. |
| [8] | Wei CHEN, Ziyang HU, Huliang DAI, Lin WANG. Extremely large-amplitude oscillation of soft pipes conveying fluid under gravity [J]. Applied Mathematics and Mechanics (English Edition), 2020, 41(9): 1381-1400. |
| [9] | Xianghong LI, Jianhua TANG, Yanli WANG, Yongjun SHEN. Approximate analytical solution in slow-fast system based on modified multi-scale method [J]. Applied Mathematics and Mechanics (English Edition), 2020, 41(4): 605-622. |
| [10] | Yunyue CONG, Houjun KANG, Tieding GUO. Analysis of in-plane 1:1:1 internal resonance of a double cable-stayed shallow arch model with cables' external excitations [J]. Applied Mathematics and Mechanics (English Edition), 2019, 40(7): 977-1000. |
| [11] | Xin LIN, Yixin HUANG, Yang ZHAO, Tianshu WANG. Large deformation analysis of a cantilever beam made of axially functionally graded material by homotopy analysis method [J]. Applied Mathematics and Mechanics (English Edition), 2019, 40(10): 1375-1386. |
| [12] | Dongxing CAO, Yanhui GAO. Free vibration of non-uniform axially functionally graded beams using the asymptotic development method [J]. Applied Mathematics and Mechanics (English Edition), 2019, 40(1): 85-96. |
| [13] | Bo WANG. Effect of rotary inertia on stability of axially accelerating viscoelastic Rayleigh beams [J]. Applied Mathematics and Mechanics (English Edition), 2018, 39(5): 717-732. |
| [14] | Qianli ZHAO, Zhili SUN. In-plane forced vibration of curved pipe conveying fluid by Green function method [J]. Applied Mathematics and Mechanics (English Edition), 2017, 38(10): 1397-1414. |
| [15] | Youqi TANG, Dengbo ZHANG, Mohan RUI, Xin WANG, Dicheng ZHU. Dynamic stability of axially accelerating viscoelastic plates with longitudinally varying tensions [J]. Applied Mathematics and Mechanics (English Edition), 2016, 37(12): 1647-1668. |
| Viewed | ||||||
|
Full text |
|
|||||
|
Abstract |
|
|||||
