Fig. 1

(a) Diagram of a practicable mechanism with weak connections. (b) Four mechanism-based elastic metamaterials which can be reconfigured from one to another (color online)"

Fig. 2

A numerical-based homogenization process of the mechanism-based metamaterial (color online)"

Table 1

Dimensionless effective material properties"

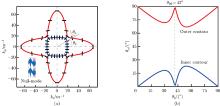
Fig. 3

(a) EFCs of in-plane wave modes and (b) polarization characteristics of the null-mode metamaterial at 10 kHz, where aluminum (ρ0=2 700 kg/m3 and E0=70 GPa) is chosen as the constituent medium. Short black solid lines at a certain interval of θk represent the polarization vectors (color online)"

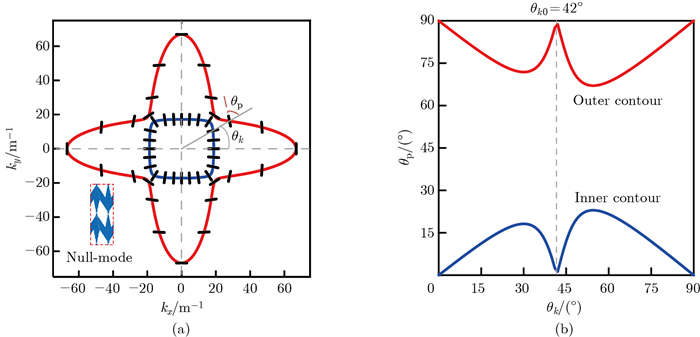
Fig. 4

(a) EFCs of in-plane wave modes and (b) polarization characteristics of the uni-mode metamaterial at 10 kHz, where aluminum (ρ0=2 700 kg/m3 and E0=70 GPa) is chosen as the constituent medium. Short black solid lines at a certain interval of θk represent polarization vectors (color online)"

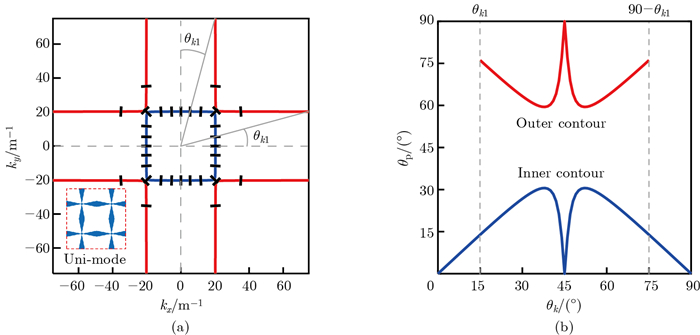
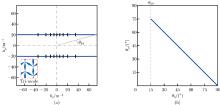
Fig. 5

(a) EFC of the in-plane wave modes and (b) polarization characteristics of the bi-mode metamaterial at 10 kHz, where aluminum (ρ0=2 700 kg/m3 and E0=70 GPa) is chosen as the constituent medium. Short black solid lines at a certain interval of θk represent polarization vectors (color online)"

Fig. 6

EFC of the in-plane wave modes of the tri-mode metamaterial at 10 kHz, where aluminum (ρ0=2 700 kg/m3 and E0=70 GPa) is chosen as the constituent medium. Short black solid lines at a certain interval of θk represent polarization vectors (color online)"

Fig. 7

(a) Schematic diagram of a 1-trit polarization filter with ternary codes ‘2’, ‘1’, and ‘0’ by programming the CF, CE, or PF configurations. (b) Simulation results of the filter at the frequency of 10 kHz with the mechanism-based metamaterials (color online)"

Fig. 8

Schematic diagram of a 2-trit-coded polarizer (color online)"

Fig. 9

Numerical demonstrations at the frequency of 10 kHz for the 2-trit polarization separation with different programmed microstructures (color online)"

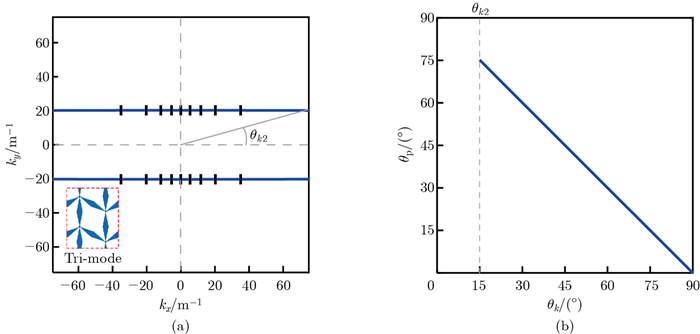
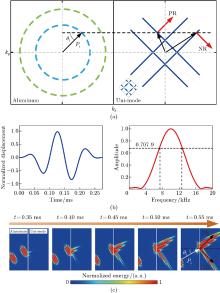
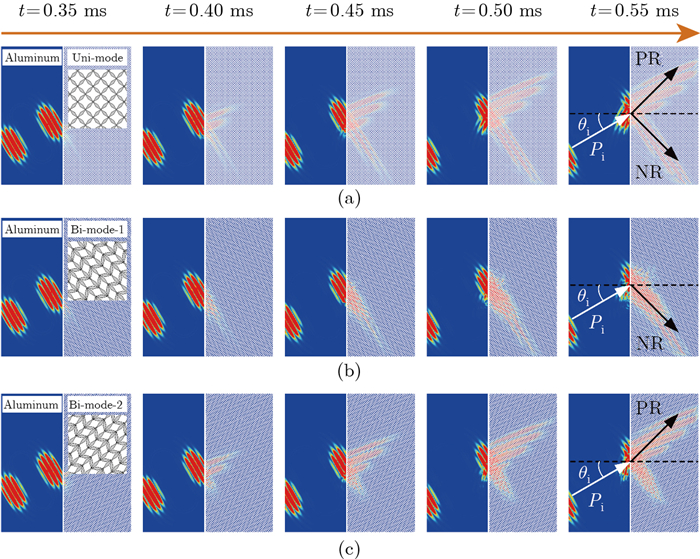
Fig. 10

(a) EFC analysis of positive-negative bi-refraction in the uni-mode metamaterial by rotating 45° counterclockwise. (b) Waveform (left) and the -3 dB frequency spectrum (right) of the tone burst signal. (c) Simulation results with the homogenized model of the uni-mode metamaterials. Pi and θi represent the energy flow orientation and the incident angle of the incident L wave, respectively. PR and NR represent positive and negative refractions, respectively (color online)"

Fig. 11

(a) EFC analysis and (b) simulation results of only-negative refraction in the homogenized model of the bi-mode metamaterial with the PF configuration in the y-direction by rotating 45° counterclockwise (color online)"

Fig. 12

(a) EFC analysis and (b) simulation results of the only-positive refraction in the homogenized model of the bi-mode metamaterial with the PF configuration in the y-direction by rotating 45° clockwise (color online)"

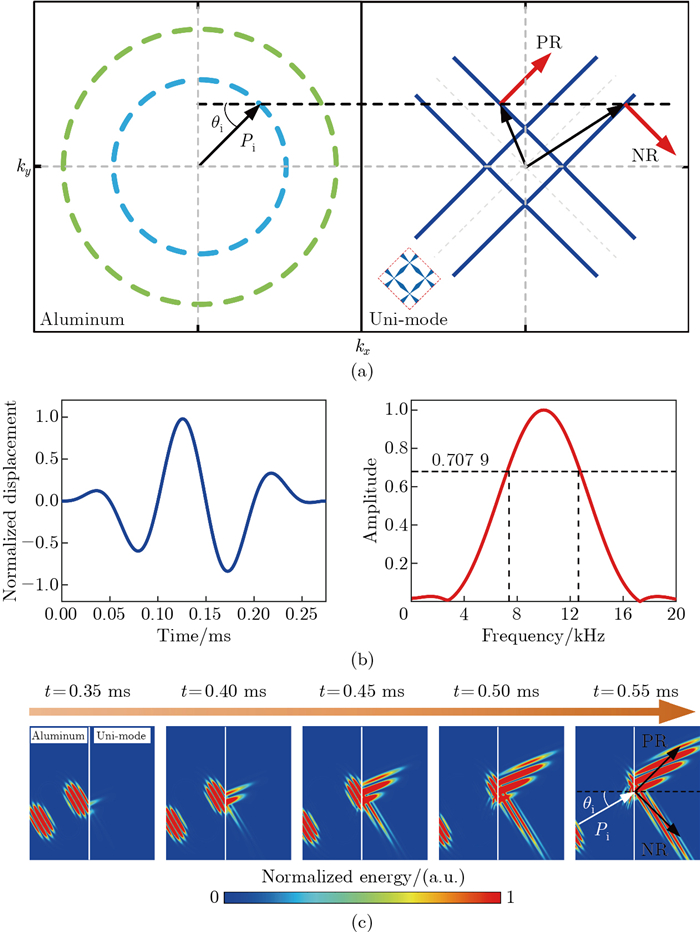
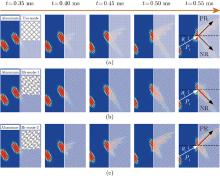
Fig. 13

Numerical validation of programmable refractions with real mechanism-based metamaterials. (a) Positive-negative bi-refraction in the uni-mode metamaterial by rotating 45° counterclockwise. (b) only-negative refraction and (c) only-positive refraction in the bi-mode metamaterial by rotating 45° counterclockwise and clockwise, respectively (color online)"