Applied Mathematics and Mechanics (English Edition) ›› 2025, Vol. 46 ›› Issue (4): 763-780.doi: https://doi.org/10.1007/s10483-025-3240-7
K. A. LUONG1, M. A. WAHAB2,3, J. H. LEE1,†( )
)
Received:2024-09-11
Revised:2025-02-08
Published:2025-04-07
Contact:
J. H. LEE, E-mail: jhlee@sejong.ac.krSupported by:2010 MSC Number:
K. A. LUONG, M. A. WAHAB, J. H. LEE. Simultaneous imposition of initial and boundary conditions via decoupled physics-informed neural networks for solving initial-boundary value problems. Applied Mathematics and Mechanics (English Edition), 2025, 46(4): 763-780.
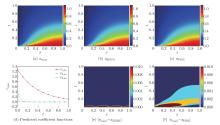
Fig. 3
Numerical results obtained by considered models for a heat transfer problem: (a) exact solution uexact; (b) dPINN solution udPINN; (c) PINN solution uPINN; (d) predicted coefficient functions by the dPINN model; (e) corresponding absolute error by the dPINN model |uexact−udPINN|; (f) corresponding absolute error by the PINN model |uexact−uPINN| (color online)"
Fig. 4
Numerical results obtained by considered models for wave propagation: (a) exact solution uexact; (b) dPINN solution udPINN; (c) PINN solution uPINN; (d) predicted coefficient functions by the dPINN model; (e) corresponding absolute error by the dPINN model |uexact−udPINN|; (f) corresponding absolute error by the PINN model |uexact−uPINN| (color online)"
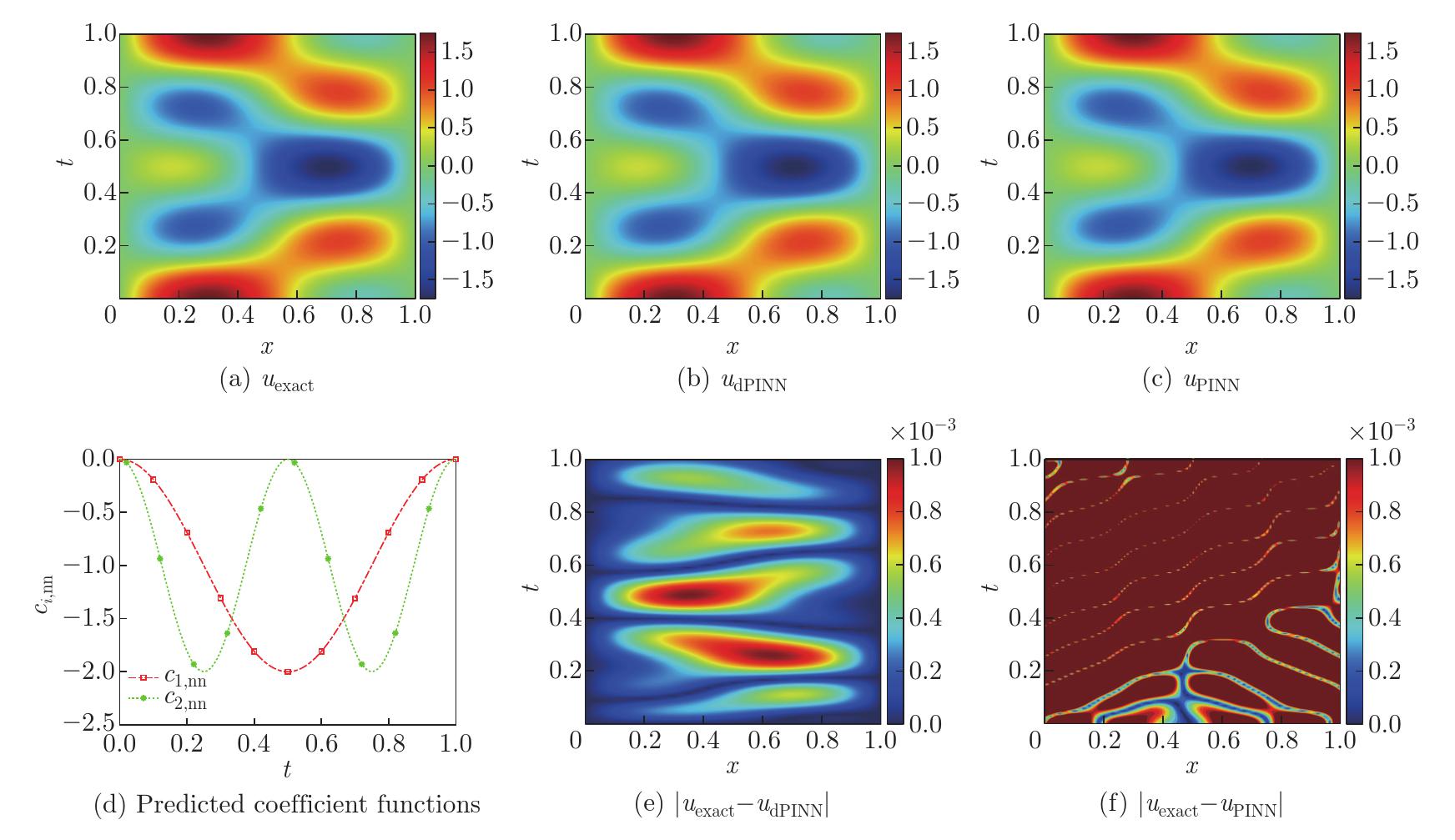

Fig. 5
Numerical results obtained by considered models for a cantilever bar problem: (a) exact solution uexact; (b) dPINN solution udPINN; (c) PINN solution uPINN; (d) predicted coefficient functions by the dPINN model; (e) corresponding absolute error by the dPINN model |uexact−udPINN|; (f) corresponding absolute error by the PINN model |uexact−uPINN| (color online)"
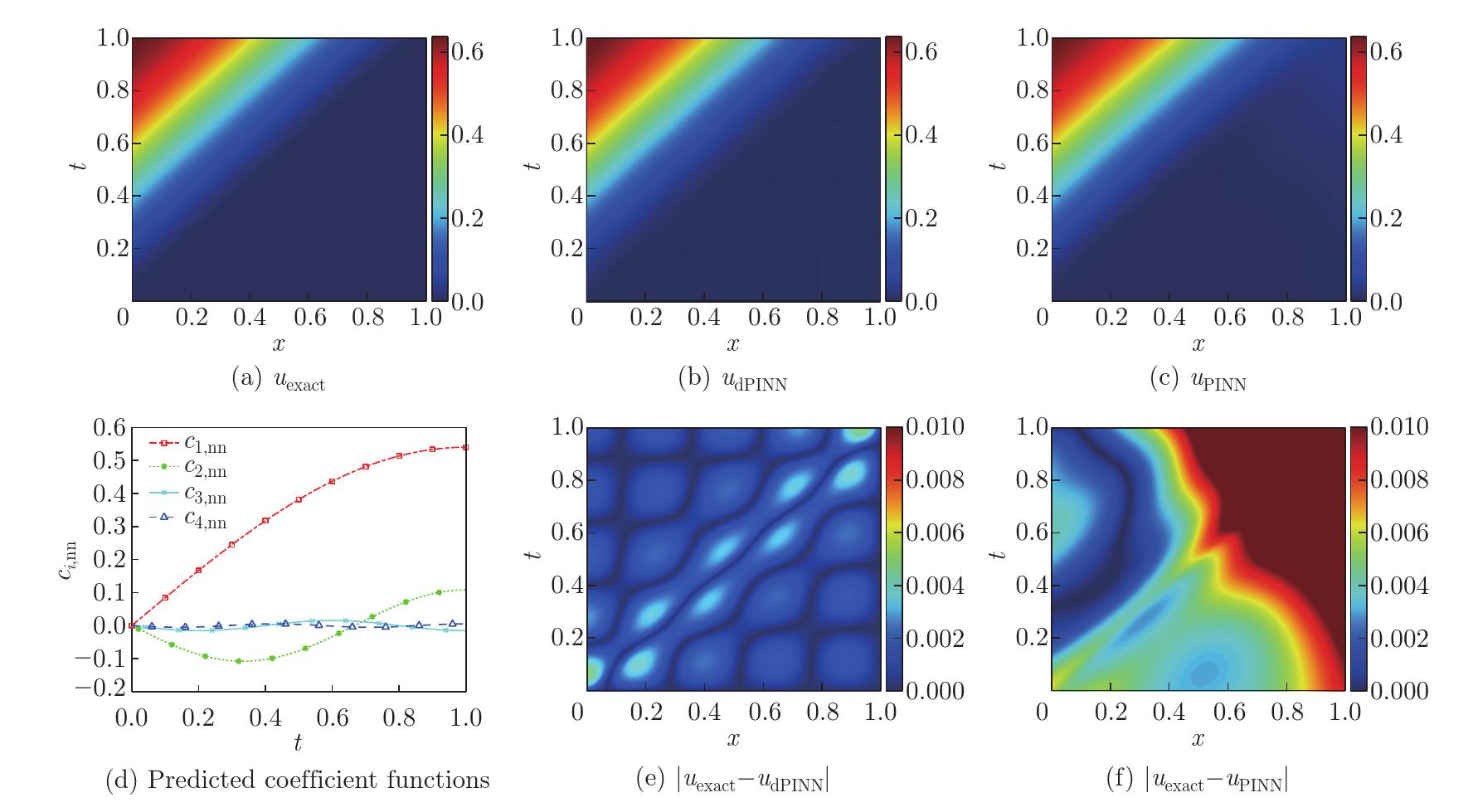
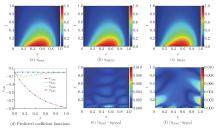
Fig. 6
Numerical results obtained by considered models for Burgers' equation: (a) exact solution uexact; (b) dPINN solution udPINN; (c) PINN solution uPINN; (d) predicted coefficient functions by the dPINN model; (e) corresponding absolute error by the dPINN model |uexact−udPINN|; (f) corresponding absolute error by the PINN model |uexact−uPINN| (color online)"
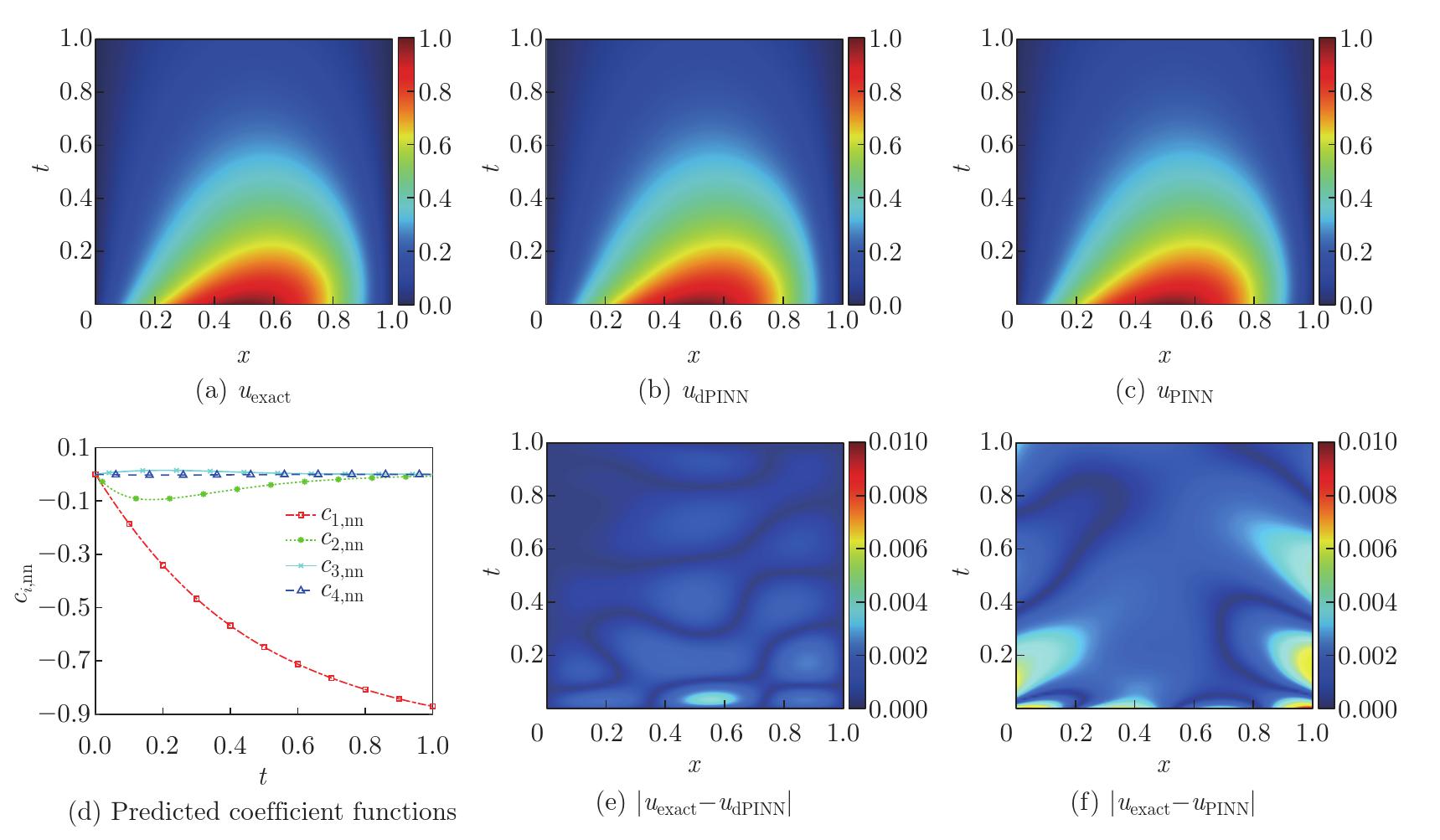

Fig. 9
Point-wise absolute errors of approximated solutions by the dPINN model and PINN model at different snapshots for an advection-diffusion equation: (a) |uexact−udPINN| at t=0.2; (b) |uexact−udPINN| at t=0.5; (c) |uexact−udPINN| at t=1.0; (d) |uexact−uPINN| at t=0.2; (e) |uexact−uPINN| at t=0.5; (f) |uexact−uPINN| at t=1.0 (color online)"
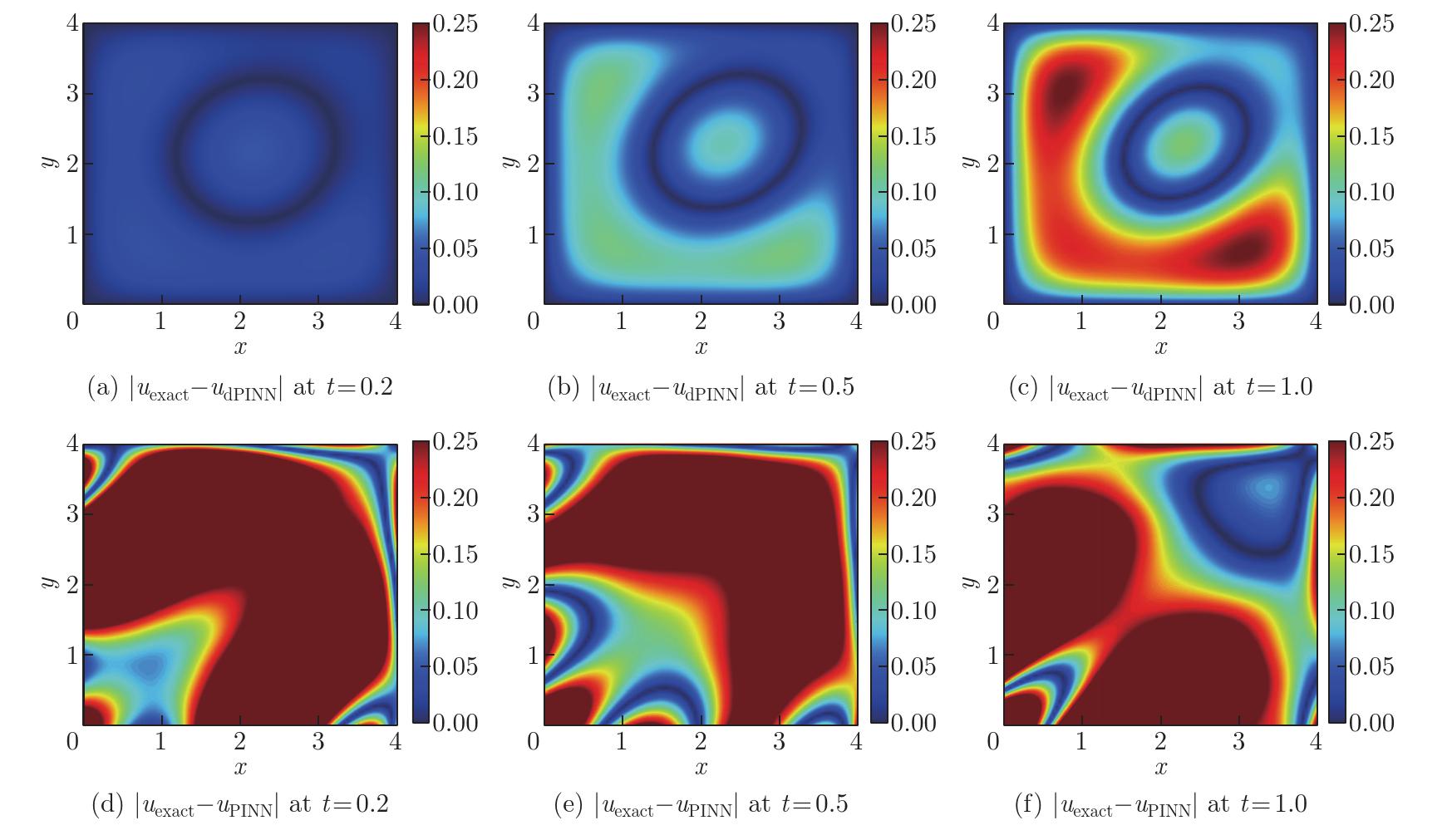
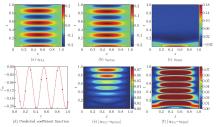
Fig. 10
Numerical results obtained by considered models for beam bending: (a) FEA's solution uFEA; (b) dPINN solution udPINN; (c) PINN solution uPINN; (d) predicted coefficient function by the dPINN model; (e) corresponding absolute error by the dPINN model |uFEA−udPINN|; (f) corresponding absolute error by the PINN model |uFEA−uPINN| (color online)"

Table 1
Comparison of training time (in minutes) of the dPINN and PINN"
| Problem | ||
|---|---|---|
| dPINN | PINN | |
| Heat transfer (see Subsection 3.1) | 0.62 | 62.43 |
| Wave propagation (see Subsection 3.2) | 1.11 | 101.55 |
| Cantilever bar (see Subsection 3.3) | 1.43 | 53.37 |
| Burgers' equation (see Subsection 3.4) | 0.84 | 46.11 |
| Advection-diffusion equation (see Subsection 3.5) | 0.80 | 192.69 |
| Fixed-beam (see Subsection 3.6) | 0.70 | 180.92 |
| [1] | TORO, E. F. Riemann Solvers and Numerical Methods for Fluid Dynamics: a Practical Introduction, Springer Science & Business Media, Berlin (2013) |
| [2] | REDDY, J. N. An Introduction to the Finite Element Method, McGraw-Hill, New York (1993) |
| [3] | MÜLLER, E. H. and SCHEICHL, R. Massively parallel solvers for elliptic partial differential equations in numerical weather and climate prediction. Quarterly Journal of the Royal Meteorological Society, 140(685), 2608–2624 (2014) |
| [4] | LEVEQUE, R. J. Finite Difference Methods for Ordinary and Partial Differential Equations: Steady-State and Time-Dependent Problems, SIAM, Philadelphia (2007) |
| [5] | KORIC, S., HIBBELER, L. C., and THOMAS, B. G. Explicit coupled thermo-mechanical finite element model of steel solidification. International Journal for Numerical Methods in Engineering, 78(1), 1–31 (2009) |
| [6] | WARBURTON, G. B. The Dynamical Behaviour of Structures, Pergamon Press, Oxford (1976) |
| [7] | DOUGLAS, J. and DUPONT, T. Galerkin methods for parabolic equations with nonlinear boundary conditions. Numerische Mathematik, 20, 213–237 (1973) |
| [8] | RAISSI, M., PERDIKARIS, P., and KARNIADAKIS, G. E. Physics-informed neural networks: a deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. Journal of Computational Physics, 378, 686–707 (2019) |
| [9] | BAYDIN, A. G., PEARLMUTTER, B. A., RADUL, A. A., and SISKIND, J. M. Automatic differentiation in machine learning: a survey. Journal of Machine Learning Research, 18(153), 1–43 (2018) |
| [10] | LE-DUC, T., LEE, S., NGUYEN-XUAN, H., and LEE, J. A hierarchically normalized physics-informed neural network for solving differential equations: application for solid mechanics problems. Engineering Applications of Artificial Intelligence, 133, 108400 (2024) |
| [11] | TRINH, D. T., LUONG, K. A., and LEE, J. An analysis of functionally graded thin-walled beams using physics-informed neural networks. Engineering Structures, 301, 117290 (2024) |
| [12] | YANG, Y. and MESRI, Y. Learning by neural networks under physical constraints for simulation in fluid mechanics. Computers & Fluids, 248, 105632 (2022) |
| [13] | YIN, M., ZHENG, X., HUMPHREY, J. D., and KARNIADAKIS, G. E. Non-invasive inference of thrombus material properties with physics-informed neural networks. Computer Methods in Applied Mechanics and Engineering, 375, 113603 (2021) |
| [14] | SUKUMAR, N. and SRIVASTAVA, A. Exact imposition of boundary conditions with distance functions in physics-informed deep neural networks. Computer Methods in Applied Mechanics and Engineering, 389, 114333 (2022) |
| [15] | LUONG, K. A., LE-DUC, T., LEE, S., and LEE, J. A novel normalized reduced-order physics-informed neural network for solving inverse problems. Engineering with Computers, 40, 3253–3272 (2024) |
| [16] | SAMANIEGO, E., ANITESCU, C., GOSWAMI, S., NGUYEN-THANH, V. M., GUO, H., HAMDIA, K., ZHUANG, X., and RABCZUK, T. An energy approach to the solution of partial differential equations in computational mechanics via machine learning: concepts, implementation and applications. Computer Methods in Applied Mechanics and Engineering, 362, 112790 (2020) |
| [17] | LI, W., BAZANT, M. Z., and ZHU, J. A physics-guided neural network framework for elastic plates: comparison of governing equations-based and energy-based approaches. Computer Methods in Applied Mechanics and Engineering, 383, 113933 (2021) |
| [18] | SCHMIDHUBER, J. Deep learning in neural networks: an overview. Neural Networks, 61, 85–117 (2015) |
| [19] | STOER, J. and BULIRSCH, R. Introduction to Numerical Analysis, Springer, New York (1980) |
| [20] | RAZZAGHI, M. and RAZZAGHI, M. Fourier series direct method for variational problems. International Journal of Control, 48(3), 887–895 (1988) |
| [21] | HORN, R. A. and JOHNSON, C. R. Matrix Analysis, Cambridge University Press, Cambridge (1985) |
| [22] | LUONG, K. A., LE-DUC, T., and LEE, J. Automatically imposing boundary conditions for boundary value problems by unified physics-informed neural network. Engineering with Computers, 40, 1717–1739 (2024) |
| [23] | ABADI, M., BARHAM, P., CHEN, J., CHEN, Z., DAVIS, A., DEAN, J., DEVIN, M., GHEMAWAT, S., IRVING, G., ISARD, M., KUDLUR, M., LEVENBERG, J., MONGA, R., MOORE, S., MURRAY, D. G., STEINER, B., TUCKER, P., VASUDEVAN, V., WARDEN, P., WICKE, M., YU, Y., and ZHENG, X. Q. TensorFlow: a system or large-scale machine learning. Proceedings of the 12th USENIX Symposium on Operating Systems Design and Implementation, Georgia, 265–283 (2016) |
| [24] | KINGMA, D. P. and BA, J. Adam: a method for stochastic optimization. International Conference on Learning Representations, California (2015) |
| [25] | LIU, D. C. and NOCEDAL, J. On the limited memory BFGS method for large scale optimization. Mathematical Programming, 45(1), 503–528 (1989) |
| [26] | MUKUNDAN, V. and AWASTHI, A. Linearized implicit numerical method for Burgers' equation. Nonlinear Engineering, 5(4), 219–234 (2016) |
| [27] | LUONG, K. A., LE-DUC, T., and LEE, J. Deep reduced-order least-square method — a parallel neural network structure for solving beam problems. Thin-Walled Structures, 191, 111044 (2023) |
| [28] | LIN, J. H., WILLIAMS, F. W., and BENNETT, P. N. Direct Ritz method for random seismic response for non-uniform beams. Structural Engineering and Mechanics: an International Journal, 2(3), 285–294 (1994) |
| [29] | KARNAKOV, P., LITVINOV, S., and KOUMOUTSAKOS, P. Solving inverse problems in physics by optimizing a discrete loss: fast and accurate learning without neural networks. PNAS Nexus, 3(1), 005 (2024) |
| [1] | Yanda WANG, Yanping LIAN, Zhidong WANG, Chunpeng WANG, Daining FANG. A novel triple periodic minimal surface-like plate lattice and its data-driven optimization method for superior mechanical properties [J]. Applied Mathematics and Mechanics (English Edition), 2024, 45(2): 217-238. |
| [2] | Jiajie GONG, Xinyue LIU, Yancong ZHANG, Fengping ZHU, Guohui HU. Prediction of single cell mechanical properties in microchannels based on deep learning [J]. Applied Mathematics and Mechanics (English Edition), 2024, 45(11): 1857-1874. |
| [3] | H. Q. YOU, X. XU, Y. YU, S. SILLING, M. D'ELIA, J. FOSTER. Towards a unified nonlocal, peridynamics framework for the coarse-graining of molecular dynamics data with fractures [J]. Applied Mathematics and Mechanics (English Edition), 2023, 44(7): 1125-1150. |
| [4] | M. KIM, G. LIN. Peri-Net-Pro: the neural processes with quantified uncertainty for crack patterns [J]. Applied Mathematics and Mechanics (English Edition), 2023, 44(7): 1085-1100. |
| [5] | Si YUAN, Quan YUAN. Condensed Galerkin element of degree m for first-order initial-value problem with O(h2m+2) super-convergent nodal solutions [J]. Applied Mathematics and Mechanics (English Edition), 2022, 43(4): 603-614. |
| [6] | Chuansai ZHOU, Haochen LI, Chen YU, Jiangjiang XIA, Pingwen ZHANG. A station-data-based model residual machine learning method for fine-grained meteorological grid prediction [J]. Applied Mathematics and Mechanics (English Edition), 2022, 43(2): 155-166. |
| [7] | Zixian ZHU, Boling GUO, Shaomei FANG. Global weak solutions to a phase-field model for motion of grain boundaries [J]. Applied Mathematics and Mechanics (English Edition), 2022, 43(11): 1777-1792. |
| [8] | Yunfei LIU, Zhaoye QIN, Fulei CHU. Nonlinear dynamic responses of sandwich functionally graded porous cylindrical shells embedded in elastic media under 1:1 internal resonance [J]. Applied Mathematics and Mechanics (English Edition), 2021, 42(6): 805-818. |
| [9] | Junning ZHANG, Shaopu YANG, Shaohua LI, Yongjie LU, Hu DING. Influence of vehicle-road coupled vibration on tire adhesion based on nonlinear foundation [J]. Applied Mathematics and Mechanics (English Edition), 2021, 42(5): 607-624. |
| [10] | Ying LIU, Yanping CHEN, Yunqing HUANG, Qingfeng LI. Analysis of a two-grid method for semiconductor device problem [J]. Applied Mathematics and Mechanics (English Edition), 2021, 42(1): 143-158. |
| [11] | Erhui WANG, Xuelan ZHANG, Liancun ZHENG, Chang SHU. Machine learning of synaptic structure with neurons to promote tumor growth [J]. Applied Mathematics and Mechanics (English Edition), 2020, 41(11): 1697-1706. |
| [12] | Jian YU, Chao YAN, Zhenhua JIANG. Revisit of dilation-based shock capturing for discontinuous Galerkin methods [J]. Applied Mathematics and Mechanics (English Edition), 2018, 39(3): 379-394. |
| [13] | Jiaqun WANG, Xiaojing LIU, Youhe ZHOU. A high-order accurate wavelet method for solving Schrödinger equations with general nonlinearity [J]. Applied Mathematics and Mechanics (English Edition), 2018, 39(2): 275-290. |
| [14] | Cong XU, Jizeng WANG, Xiaojing LIU, Lei ZHANG, Youhe ZHOU. Coiflet solution of strongly nonlinear p-Laplacian equations [J]. Applied Mathematics and Mechanics (English Edition), 2017, 38(7): 1031-1042. |
| [15] | Jianzhong ZHAO, Xingming GUO, Lu LU. Controlled wrinkling analysis of thin films on gradient substrates [J]. Applied Mathematics and Mechanics (English Edition), 2017, 38(5): 617-624. |
| Viewed | ||||||
|
Full text |
|
|||||
|
Abstract |
|
|||||


 Email Alert
Email Alert RSS
RSS