Applied Mathematics and Mechanics (English Edition) ›› 2024, Vol. 45 ›› Issue (7): 1139-1154.doi: https://doi.org/10.1007/s10483-024-3163-9
• Articles • Previous Articles Next Articles
Yuxin YAO1,2, Yuansheng MA1,2, Fang HONG1,2, Kai ZHANG1,2,3,*( ), Tingting WANG1,2, Haijun PENG3, Zichen DENG1,2
), Tingting WANG1,2, Haijun PENG3, Zichen DENG1,2
Received:2024-03-29
Online:2024-07-03
Published:2024-06-29
Contact:
Kai ZHANG
E-mail:kzhang@nwpu.edu.cn
Supported by:2010 MSC Number:
Yuxin YAO, Yuansheng MA, Fang HONG, Kai ZHANG, Tingting WANG, Haijun PENG, Zichen DENG. On Klein tunneling of low-frequency elastic waves in hexagonal topological plates. Applied Mathematics and Mechanics (English Edition), 2024, 45(7): 1139-1154.
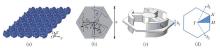
Fig. 1
(a) Schematic of the periodic structure and (b) schematic of the unit cell. The figure shows the corresponding positions of the structural parameters, and the specific parameter values are shown in Table 1. (c) The longitudinal diagram of the unit cell. (d) Within the reciprocal lattice space, the first Brillouin zone is identified, with its fundamental sector highlighted in blue, representing the irreducible portion of the first Brillouin zone (color online)"
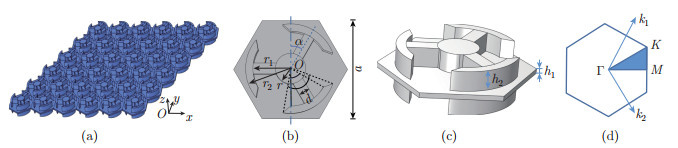

Fig. 2
(a)-(c) Out-of-plane band structures of (a) α = 0º (named as Unit cell B), (b) α = 30º (named as Unit cell C), and (c) α = -30º (named as Unit cell D). The Dirac point formed by Dirac degeneracy in (a) is marked by a black dot, and the opened out-of-plane bandgaps in (b) and (c) are represented by gray regions (color online)"
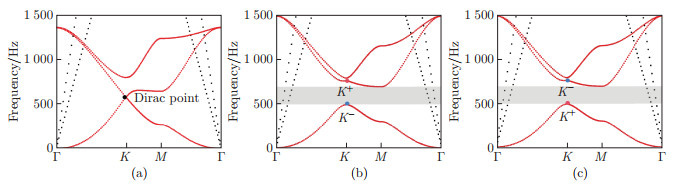

Fig. 3
Analysis of modes with topological properties: (a) the connection between the bandwidth and the rotation angle α of the prism, where the solid lines indicate the bandwidths of Cells C and D at the wave vector k; (b) kinetic energy distributions of Unit cells C and D in (a). The color represents the amplitude of the kinetic energy Wk, where the energy distribution of Unit cells C and D reveals the opposite chirality, which indicates a topological phase transition; (c) the top views of the out-of-plane phases of Unit cells C and D in (a), and the in-plane displacement is almost invisible, where the color represents the amplitude of the out-of-plane displacement (color online)"

Fig. 4
Schematic dispersion curves and modes of the supercell. (a) Schematic of the supercell, in which Cells D and C are marked in blue and orange, respectively. (b) Dispersion curves of the supercell, where the blue and gray curves are the topological edge modes. E1/F1 and E2/F2 mark the eigenfrequencies of the edge states at wave vectors k=-0.5 and k=0.5, respectively (color online)"
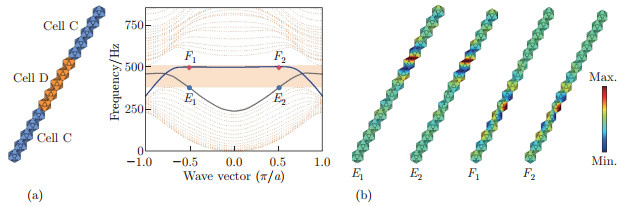

Fig. 5
Dispersion curves of the supercell and the topological edge eigenstates at a particular point. (a) Schematic of the supercell and topological edge modes, where the green, blue, and orange cells are Cells B, C, and D, respectively. (b) Dispersion curves of the supercell, where the blue curve is the valley-locked edge state, and the shaded zone is the theoretical bandgap. G1 and G2 are the eigenfrequencies at k = -0.8 and k = 0.8, respectively. The right panels show the eigenstate of topological edges at G1 and G2 (color online)"
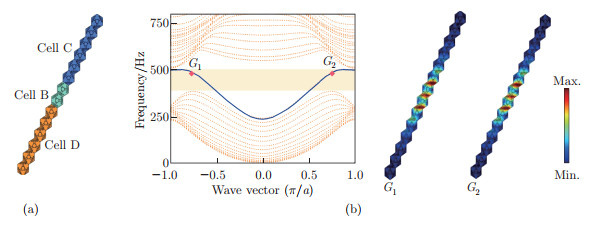
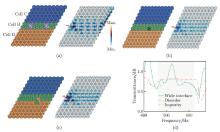
Fig. 6
At a frequency of 525 Hz, the displacement field characteristics of valley-locked elastic waves are as follows: (a) the schematic of the phononic crystal plate composed of Cells B, C, and D, where the green, blue, and orange cells are Cells B, C, and D, respectively, regions S1 and S2 within the range of Cells B are selected to calculate the transmission rate and are marked in light purple, and the red arrow marks the excitation position; (b) waveguide under impurity, where cells with dark green color in the inserted panel denote the local impurity; (c) waveguide under local disorder; (d) transmittance of valley-locked elastic waves under wide interface, impurity, and local disorders. The shaded area marks the theoretical bandgap (color online)"
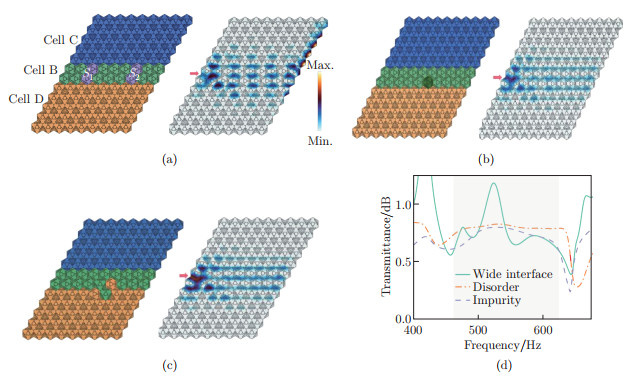
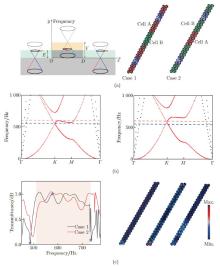
Fig. 7
Klein tunneling of elastic waves: (a) a conical dispersion profile associated with the Klein tunneling, defined by an energy barrier of the amplitude V and a lateral dimension of D, where the red and blue lines signify branches with contrary pseudospin orientations, mirroring the properties of a massless relativistic Dirac quasiparticle, two types of composite panels consist of Cells A and B (marked as red and green, respectively), and regions S1 and S2 (labeled as light purple) are the integral areas of calculating transmission; (b) dispersion curves of Cells A and B, where the red shaded area represents the barrier; (c) transmittance of the designed two composite plates and displacement fields corresponding to the frequencies 480 Hz, 575 Hz, and 740 Hz of the star on the transmittance (color online)"
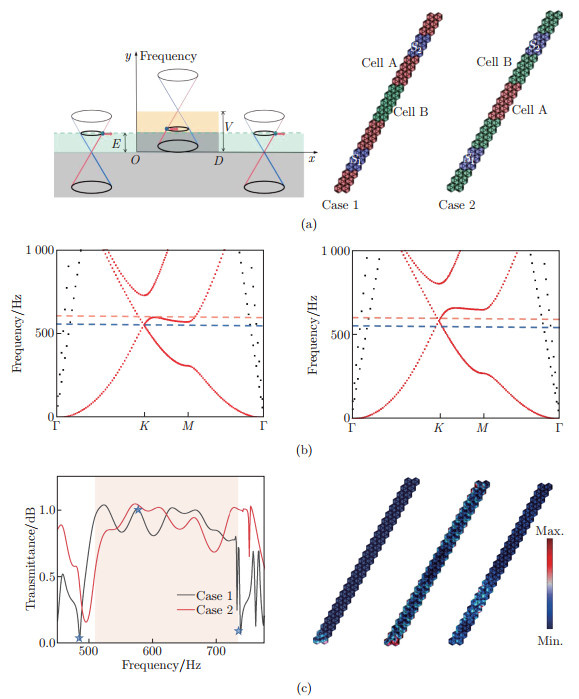
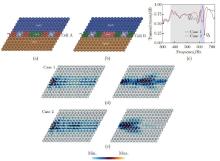
Fig. 9
Schematics of phononic crystal plates and transmittance: (a) Case 1, Cell B is inserted into Cell A as a potential barrier; (b) Case 2, Cell A is inserted into Cell B as a potential well, where the red, green, blue, and orange cells are Cells A, B, C, and D, respectively. In Case 1 (Case 2), regions S1 and S2 within the range of Cell A (Cell B) are selected to calculate the transmission rate, and are marked in light purple, and the position of the black arrow indicates the excitation; (c) transmittances of Cases 1 and 2, where the frequencies of Points Q1 and Q2 are 525 Hz and 642 Hz, respectively; (d) and (e) displacement fields for Cases 1 and 2 at two frequency points, respectively (color online)"
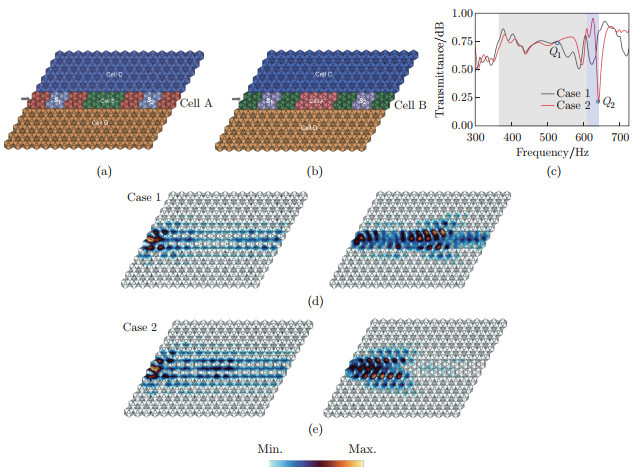

Fig. 10
Elastic wave splitter: (a) schematic diagram of Case 1 phononic crystal plate, where the red, green, blue, and orange cells are cells A, B, C, and D, respectively. Cell B is inserted into Cell A as a potential barrier. The input port is indicated by the black arrow, denoted as I; the output ports are indicated by blue arrows, denoted as O1 and O2; (b) transmission of outputs O1 and O2 is derived from the simulation study. The light gray shade and the light purple shade represent two frequency intervals, and the three frequency points are marked with stars; (c)-(e) displacement fields under different frequencies obtained from simulation: (c) 575 Hz, (d) 606 Hz, and (e) 640 Hz (color online)"
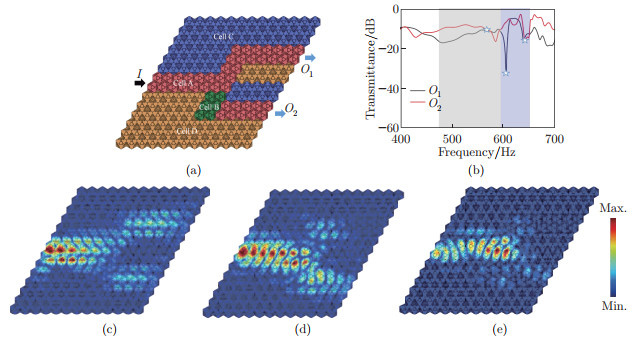

Fig. 11
Elastic wave splitter: (a) schematic diagram of Case 2 phononic crystal plate, where the red, green, blue, and orange cells are cells A, B, C, and D, respectively. Cell A is inserted into Cell B as a potential barrier. The input port is indicated by the black arrow, denoted as I; the output ports are indicated by blue arrows, denoted as O1 and O2; (b) transmittance of outputs O1 and O2 obtained from simulation, where the light gray shade and the light orange shade represent two frequency intervals, and the two frequency points are marked with stars; (c) displacement field at the frequency of 575 Hz; (e) displacement field at the frequency of 636 Hz (color online)"
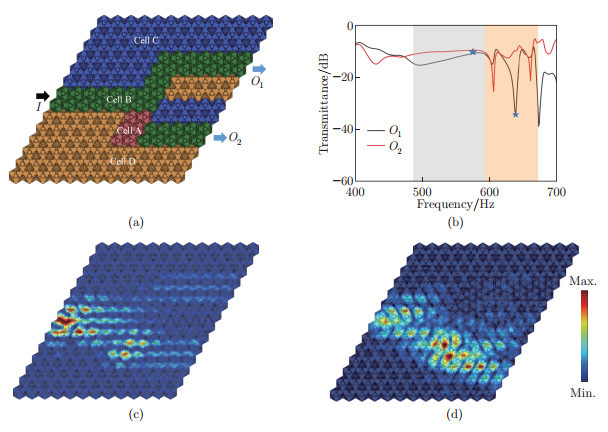
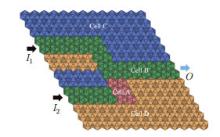
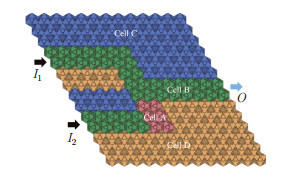
Fig. 12
Schematic diagram of a phononic crystal plate, where the red, green, blue, and orange cells are Cells A, B, C, and D, respectively. Cell A is inserted into Cell B as a potential barrier. The input ports are indicated by the black arrow, denoted as I1 and I2; the output port is indicated by blue arrows, denoted as O (color online)"
| 1 | HUANG, H., HUO, S., and CHEN, J. Subwavelength elastic topological negative refraction in ternary locally resonant phononic crystals. International Journal of Mechanical Sciences, 198, 106391 (2021) |
| 2 | YANG, L., YU, K., BONELLO, B., DJAFARI-ROUHANI, B., WANG, W., and WU, Y. Abnormal topological refraction into free medium at subwavelength scale in valley phononic crystal plates. Physical Review B, 103 (18), 184303 (2021) |
| 3 | AGUZZI, G., KANELLOPOULOS, C., WILTSHAW, R., CRASTER, R. V., CHATZI, E. N., and COLOMBI, A. Octet lattice-based plate for elastic wave control. Scientific Reports, 12 (1), 1088 (2022) |
| 4 | ZHAO, P., ZHANG, K., and DENG, Z. Elastic wave propagation in lattice metamaterials with Koch fractal. Acta Mechanica Solida Sinica, 33 (5), 600- 611 (2020) |
| 5 | YAN, G., YAO, S., and LI, Y. Propagation of elastic waves in metamaterial plates with various lattices for low-frequency vibration attenuation. Journal of Sound and Vibration, 536, 117140 (2022) |
| 6 | ZHOU, J., DONG, C., WANG, Z., CHEN, B., QIN, R., and NIU, X. Approaching ideal energy absorption through the multicellular structure with gradient material distribution. International Journal of Mechanical Sciences, 225, 107355 (2022) |
| 7 | ZHANG, K., LUO, J., HONG, F., and DENG, Z. Seismic metamaterials with cross-like and square steel sections for low-frequency wide band gaps. Engineering Structures, 232, 111870 (2021) |
| 8 | HAJJAJ, M. M., and TU, J. A seismic metamaterial concept with very short resonators using depleted uranium. Archive of Applied Mechanics, 91 (5), 2279- 300 (2021) |
| 9 | KACIN, S., OZTURK, M., SEVIM, U. K., MERT, B. A., OZER, Z., AKGOL, O., UNAL, E., and KARAASLAN, M. Seismic metamaterials for low-frequency mechanical wave attenuation. Natural Hazards, 107 (1), 213- 29 (2021) |
| 10 | LIU, X., ZHANG, K., SHI, H., HONG, F., LIU, H., and DENG, Z. Origami-inspired metamaterial with compression-twist coupling effect for low-frequency vibration isolation. Mechanical Systems and Signal Processing, 208, 111076 (2024) |
| 11 | SHI, H., ZHANG, K., LIU, X., LIU, H., PENG, H., and DENG, Z. Vibration suppression of a meta-structure with hybridization of Kresling origami and waterbomb-based origami. Composite Structures, 334, 117964 (2024) |
| 12 | MAO, J. J., WANG, S., TAN, W., and LIU, M. Modular multistable metamaterials with reprogrammable mechanical properties. Engineering Structures, 272, 114976 (2022) |
| 13 | CHEN, T., PAULY, M., and REIS, P. M. A reprogrammable mechanical metamaterial with stable memory. nature, 589 (7842), 386- 90 (2021) |
| 14 | KURGANOV, G., DOBRYKH, D., PUHTINA, E., YUSUPOV, I., SLOBOZHANYUK, A., KIVSHAR, Y. S., and ZHIRIHIN, D. Temperature control of electromagnetic topological edge states. Applied Physics Letters, 120 (23), 233105 (2022) |
| 15 | ZHANG, J., JIANG, Y. P., MA, X. C., and XUE, Q. K. Berry-phase switch in electrostatically confined topological surface states. Physical Review Letters, 128 (12), 126402 (2022) |
| 16 | ZHANG, K., HONG, F., LUO, J., and DENG, Z. Topological edge state analysis of hexagonal phononic crystals. Acta Mechanica Sinica, 38 (3), 421455 (2022) |
| 17 | TIAN, Z., SHEN, C., LI, J., REIT, E., BACHMAN, H., SOCOLAR, J. E. S., CUMMER, S. A., and HUANG, J. T. Dispersion tuning and route reconfiguration of acoustic waves in valley topological phononic crystals. Nature Communications, 11 (1), 762 (2020) |
| 18 | DU, J., LI, T., FAN, X., ZHANG, Q., and QIU, C. Acoustic realization of surface-obstructed topological insulators. Physical Review Letters, 128 (22), 224301 (2022) |
| 19 | YUE, Z., ZHANG, Z., WANG, H. X., XIONG, W., CHENG, Y., and LIU, X. Glided acoustic higher-order topological insulators based on spoof surface acoustic waves. New Journal of Physics, 24 (5), 053009 (2022) |
| 20 | GAO, H., XUE, H., GU, Z., LIU, T., ZHU, J., and ZHANG, B. Non-Hermitian route to higher-order topology in an acoustic crystal. Nature Communications, 12 (1), 1888 (2021) |
| 21 | ZHANG, K., HONG, F., LUO, J., and DENG, Z. Topological insulator in a hexagonal plate with droplet holes. Journal of Physics D: Applied Physics, 54 (10), 105502 (2020) |
| 22 | GANTI, S. S., LIU, T. W., and SEMPERLOTTI, F. Weyl points and topological surface states in a three-dimensional sandwich-type elastic lattice. New Journal of Physics, 22 (8), 083001 (2020) |
| 23 | HONG, F., ZHANG, K., QI, L., DING, B., and DENG, Z. High-frequency topological corner and edge states in elastic honeycomb plates. International Journal of Mechanical Sciences, 246, 108141 (2023) |
| 24 | MINIACI, M., and PAL, R. K. Design of topological elastic waveguides. Journal of Applied Physics, 130 (14), 141101 (2021) |
| 25 | LIU, S., SHAO, R., MA, S., ZHANG, L., YOU, O., WU, H., XIANG, Y. J., CUI, T. J., and ZHANG, S. Non-Hermitian skin effect in a non-Hermitian electrical circuit. Research, 2021, 5608038 (2021) |
| 26 | LI, Y., LIANG, C., WANG, C., LU, C., and LIU, Y. C. Gain-loss-induced hybrid skin-topological effect. Physical Review Letters, 128 (22), 223903 (2022) |
| 27 | LU, C., SUN, Y. Z., WANG, C., ZHANG, H., ZHAO, W., HU, X., XIAO, M., DING, W., LIU, Y. C., and CHAN, C. T. On-chip nanophotonic topological rainbow. Nature Communications, 13 (1), 2586 (2022) |
| 28 | SUI, F., CHEN, J., and HUANG, H. Tunable topological edge states and rainbow trapping in two dimensional magnetoelastic phononic crystal plates based on an external magnetostatic field. International Journal of Mechanical Sciences, 225, 107360 (2022) |
| 29 | LEE, M. J., and OH, I. K. Robust separation of topological in-plane and out-of-plane waves in a phononic crystal. Communications Physics, 5 (1), 17 (2022) |
| 30 | ZHAO, Y., LIANG, F., HAN, J., WANG, X., ZHAO, D., and WANG, B. Z. Tunable topological edge and corner states in an all-dielectric photonic crystal. Optics Express, 30 (22), 40515 (2022) |
| 31 | TANG, G. J., HE, X. T., SHI, F. L., LIU, J. W., CHEN, X. D., and DONG, J. W. Topological photonic crystals: physics, designs, and applications. Laser & Photonics Reviews, 16 (4), 2100300 (2022) |
| 32 | NI, A., and SHI, Z. Robust elastic wave transport in zone-folding induced topological hierarchical metamaterials. International Journal of Mechanical Sciences, 251, 108336 (2023) |
| 33 | CHEN, Z., and ZHOU, W. Temperature-controlled elastic wave transport in topological ferroelectric phononic crystal plates. International Journal of Mechanical Sciences, 241, 107964 (2023) |
| 34 | MA, Z., LIU, Y., XIE, Y. X., and WANG, Y. S. A simple elastic phononic crystal plate with adjustable topological valley transmission paths. Extreme Mechanics Letters, 57, 101910 (2022) |
| 35 | GAO, N., WANG, J., and CHEN, W. Klein tunneling for Lamb waves in elastic phononic crystal plates. Applied Physics Letters, 121 (10), 102201 (2022) |
| 36 | ZHANG, Y., WANG, C., and HUANG, L. A tunable electromagnetic acoustic switch. Applied Physics Letters, 116 (18), 183502 (2020) |
| 37 | CHEN, K., DONG, X., GAO, P., ZHANG, J., SUN, Y., TU, G., and PENG, Z. Multifunctional applications of topological valley-locked elastic waves. International Journal of Mechanical Sciences, 259, 108589 (2023) |
| 38 | LIU, C., TIAN, Y., ZHANG, Y., and TAN, Z. Tunable topological edge states and energy harvesting of piezoelectric-inductance phononic crystals based on Su-Schrieffer-Heeger model. Physics Letters A, 506, 129470 (2024) |
| 39 | PIRIE, H., SADHUKA, S., WANG, J., ANDREI, R., and HOFFMAN, J. E. Topological phononic logic. Physical Review Letters, 128 (1), 015501 (2022) |
| 40 | WEN, Z., JIN, Y., GAO, P., ZHUANG, X., RABCZUK, T., and DJAFARI-ROUHANI, B. Topological cavities in phononic plates for robust energy harvesting. Mechanical Systems and Signal Processing, 162, 108047 (2022) |
| 41 | LAN, C., HU, G., TANG, L., and YANG, Y. Energy localization and topological protection of a locally resonant topological metamaterial for robust vibration energy harvesting. Journal of Applied Physics, 129 (18), 184502 (2021) |
| [1] | Zhou HU, Zhibo WEI, Yan CHEN, Rui ZHU. Reconfigurable mechanism-based metamaterials for ternary-coded elastic wave polarizers and programmable refraction control [J]. Applied Mathematics and Mechanics (English Edition), 2024, 45(7): 1225-1242. |
| [2] | Jiangcheng CAI, Mingxi DENG. Mathematical framework of nonlinear elastic waves propagating in pre-stressed media [J]. Applied Mathematics and Mechanics (English Edition), 2024, 45(10): 1705-1716. |
| [3] | Shengjie YAO, Yijun CHAI, Xiongwei YANG, Yueming LI. Elastic twisting metamaterial for perfect longitudinal-torsional wave mode conversion [J]. Applied Mathematics and Mechanics (English Edition), 2023, 44(4): 515-524. |
| [4] | Wanli YANG, Jinxi LIU, Yizhan YANG, Yuantai HU. The mechanism to reform dynamic performance of an elastic wave-front in a piezoelectric semiconductor by the wave-carrier interaction induced from static biasing fields [J]. Applied Mathematics and Mechanics (English Edition), 2023, 44(3): 381-396. |
| [5] | Zhenni LI, Yize WANG, Yuesheng WANG. Tunable three-dimensional nonreciprocal transmission in a layered nonlinear elastic wave metamaterial by initial stresses [J]. Applied Mathematics and Mechanics (English Edition), 2022, 43(2): 167-184. |
| [6] | Chenxu QIANG, Yuxin HAO, Wei ZHANG, Jinqiang LI, Shaowu YANG, Yuteng CAO. Bandgaps and vibration isolation of local resonance sandwich-like plate with simply supported overhanging beam [J]. Applied Mathematics and Mechanics (English Edition), 2021, 42(11): 1555-1570. |
| [7] | Hong XIA, Zhendong LUO. Optimized finite difference iterative scheme based on POD technique for 2D viscoelastic wave equation [J]. Applied Mathematics and Mechanics (English Edition), 2017, 38(12): 1721-1732. |
| [8] | Junbo CHENG. Harten-Lax-van Leer-contact (HLLC) approximation Riemann solver with elastic waves for one-dimensional elasticplastic problems [J]. Applied Mathematics and Mechanics (English Edition), 2016, 37(11): 1517-1538. |
| [9] | Chuan-ping ZHOU;Chao HU;F. MA;Dian-kui LIU. Dynamic stress concentrations in thick plates with two holes based on refined theory [J]. Applied Mathematics and Mechanics (English Edition), 2014, 35(12): 1591-1606. |
| [10] | M. KUMAR;R. SAINI. Reflection and refraction of attenuated waves at boundary of elastic solid and porous solid saturated with two immiscible viscous fluids [J]. Applied Mathematics and Mechanics (English Edition), 2012, 33(6): 797-816. |
| [11] | HOU Xiu-Hui;DENG Zi-Chen;ZHOU Jia-Xi. Symplectic analysis for wave propagation in one-dimensional nonlinear periodic structures [J]. Applied Mathematics and Mechanics (English Edition), 2010, 31(11): 1371-1382. |
| [12] | Payel Das;Mridula Kanoria. Magneto-thermo-elastic waves in an infinite perfectly conducting elastic solid with energy dissipation [J]. Applied Mathematics and Mechanics (English Edition), 2009, 30(2): 221-228 . |
| [13] | LI Lin;ZHOU Zhen-gong;WANG Biao. SCATTERING OF ANTI-PLANE SHEAR WAVES IN A FUNCTIONALLY GRADED MATERIAL STRIP WITH AN OFF-CENTER VERTICAL CRACK [J]. Applied Mathematics and Mechanics (English Edition), 2006, 27(6): 731-739 . |
| [14] | SUN Jian-liang;ZHOU Zhen-gong;WANG Biao. DYNAMIC BEHAVIOR OF TWO UNEQUAL PARALLEL PERMEABLE INTERFACE CRACKS IN A PIEZOELECTRIC LAYER BONDED TO TWO HALF PIEZOELECTRIC MATERIALS PLANES [J]. Applied Mathematics and Mechanics (English Edition), 2005, 26(2): 160-170 . |
| [15] | QU Gui-min;ZHOU Zhen-gong;WANG Biao. DYNAMIC BEHAVIOR OF TWO COLLINEAR PERMEABLE CRACKS IN A PIEZOELECTRIC LAYER BONDED TO TWO HALF SPACES [J]. Applied Mathematics and Mechanics (English Edition), 2005, 26(10): 1266-1276 . |
| Viewed | ||||||
|
Full text |
|
|||||
|
Abstract |
|
|||||


 Email Alert
Email Alert RSS
RSS