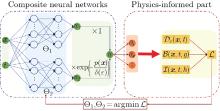
Fig. 1

The architecture of the C-PINN method. The C-PINN method utilizes a composite structure known as the composite neural network for the approximate solution u. This structure consists of two sub-neural networks, each with inputs (x, t) and outputs u1 and u2. The output u2 is multiplied by an exponential factor . The loss function is determined by substituting the composite neural network into the governing equation, boundary conditions, and initial conditions, resulting in three terms: (color online)"

Fig. 2

Results for the singularly perturbed linear ODE problem (see Eq. (12) and the boundary conditions) with α = 0, β = 1, and ε = 0.001 (color online)"

Fig. 3

Results for the singularly perturbed nonlinear ODE problem (see Eq. (15) and the boundary conditions) with ε = 0.001 (color online)"

Fig. 4

Results for the singularly perturbed elliptic PDE problem (see Eq. (17) and the boundary conditions) with ε=0.001 (color online)"

Fig. 5

Results for the singularly perturbed parabolic PDE problem (see Eq. (20) and the initial and boundary conditions) with ε = 0.001 (color online)"

Fig. 6

Results for the singularly perturbed hyperbolic PDE problem (see Eq. (22) and the initial and boundary conditions) with ε=0.001 (color online)"

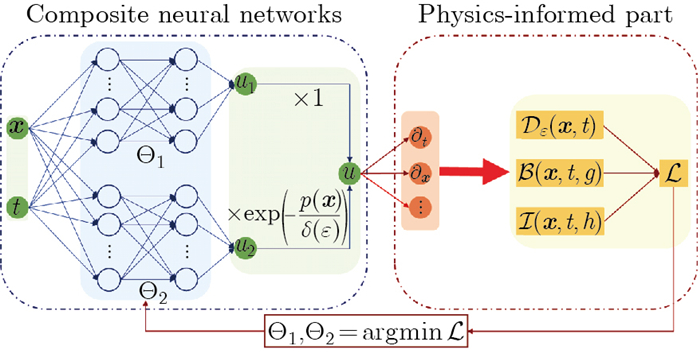
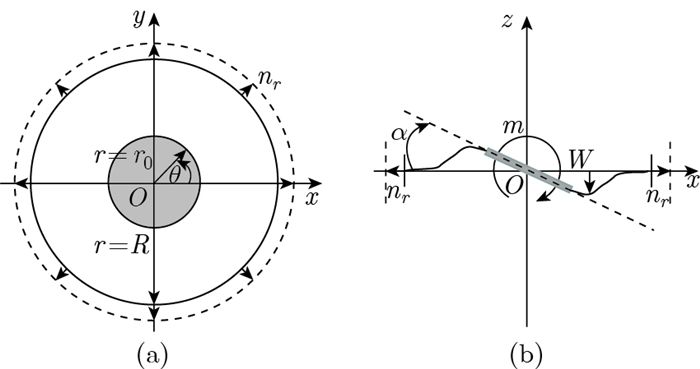
Fig. 7

The unsymmetrical bending problem of an annular plate: (a) the top view of the annular plate, where the outer radius of the annular plate is R, a central rigid inclusion with a radius of r0 is embedded into the center of the plate, and the plate is subject to the uniform radial prestress without surface load; (b) the side view of the annular plate, where the outer edge of the plate is clamped, and a moment m is applied to the rigid inclusion which rotates about the y-axis with an angle α, leading to the bending of the plate with a lateral displacement W"

Fig. 8

Results for the unsymmetrical bending problem of prestressed annular plates with dual boundary layers (color online)"