Fig. 1

The network framework for solving the hyperelastic-magnetic coupling problems without external currents (color online)"

Fig. 2

The network framework for solving the hyperelastic-magnetic coupling problems with an external current (color online)"

Fig. 3

The geometrical and boundary conditions of the elliptic ring: (a) schematic of geometry and boundary conditions and (b) distribution of the background magnetic field (color online)"

Fig. 4

The convergence curve of the loss function utilizing the "Adam + L_BFGS" optimization strategy (color online)"

Fig. 5

Displacement (mm) and the first PK stress (MPa) results predicted by the PINN (color online)"

Fig. 6

Absolute errors for the PINN prediction of magnetically induced deformation of the elliptic ring (color online)"

Fig. 7

Magnetic scalar potential and magnetic field prediction results predicted by the PINN and the corresponding absolute errors (denoted with (·)*) (color online)"

Fig. 8

Comparison curves between the PINN prediction and the reference results along the line AD: (a) the vertical displacement and (b) the Mises stress (color online)"

Fig. 9

Mechanical model of a robotic arm, consisting of a rigid arm and an MRE joint (color online)"

Fig. 10

Cloud map depicting the PINN prediction of magnetic motion results for the robotic arm: (a) the vertical displacement and (b) the Mises stress (color online)"

Fig. 11

CPU time of the FEM calculation and PINN prediction under different unit nodes and test points (color online)"

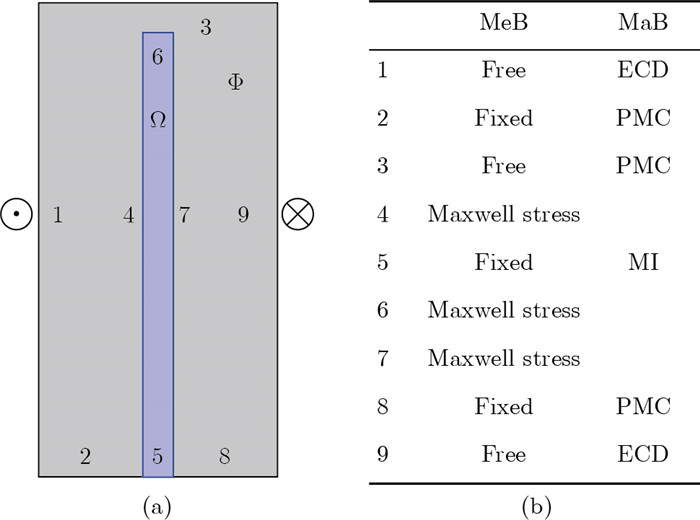
Fig. 12

Model for magnetically induced bending of cantilever beams: (a) the geometric structure and (b) the boundary conditions, where MeB and MaB represent mechanical and magnetic boundaries, respectively, ECD denotes the external current density, PMC denotes the perfect magnetic conductor, and MI stands for the magnetic insulation (color online)"

Fig. 13

Allocation with labeled points under different strategies: (a) the increased number of points at the 4 corners of the cantilever beam and (b) the randomly allocated points (color online)"

Fig. 14

PINN prediction of the displacements and the first PK stresses alongside the corresponding absolute error plots for the cantilever beam region (color online)"

Fig. 15

PINN prediction of the magnetic vector potentials and the flux densities alongside the corresponding absolute errors in the air and MRE regions (color online)"

Table 1

Comparison of the MSEs between the PINN and ANN prediction results and reference values under different numbers of label points"

Fig. 16

Cloud plots of predicted results for the magnetic vector potential and magnetic flux density for 100 labeled data points: (a) ANN prediction results and (b) PINN prediction results (color online)"