Fig. 1

PINN architecture for hyperelastic solid mechanics and the training procedure, where each independent network consists of 5 hidden layers with 30 neurons per hidden layer (color online)"

Fig. 2

Schematic of the TL-PINN in this work, where in each independent network, the flrst three hidden layers are frozen (blue lines), while the subsequent two hidden layers keep flne-tuning (red lines) (color online)"

Fig. 3

The PINN model solving the forward problem for the compressible Neo-Hookean hyperelastic model: (a) the forward problem setup with a displacement load; (b) the decreasing history of the loss function, normalized by its initial value; (c) the PINN inference and (d) the FEM reference of the full-fleld domain (color online)"

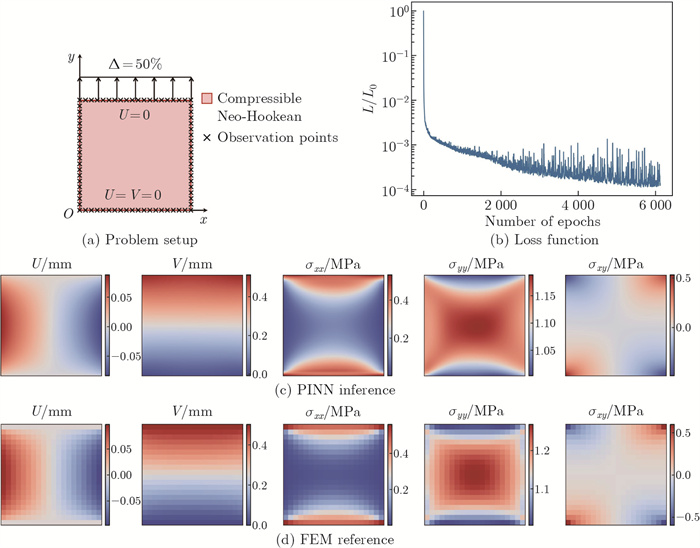
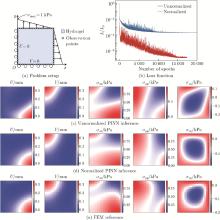
Fig. 4

The PINN model solving the forward problem for hydrogels: (a) the forward problem setup with a biaxial triangular force load; (b) the decreasing history of the loss functions with the normalized PINN trained over 20 000 epochs and the unnormalized PINN over 17 400 epochs; the predicted full-fleld solutions using (c) unnormalized and (d) normalized PINNs, respectively; (e) the FEM reference (color online)"

Fig. 5

Comparison of boundary constraint strategies for parameter identiflcation in hydrogels: (a) without BC constraints; (b) with soft BC constraints; (c) with hard BC constraints (color online)"

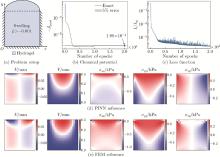
Fig. 6

Prediction results for the inverse problem of hydrogel swelling under chemical potential stimuli: (a) the problem setup, with the left, bottom, and right edges flxed; (b) the convergence history of the chemical potential , achieving a relative error of 0.82%; (c) the decreasing history of the loss function; (d) the continuous full-fleld solution output by the network; (e) the FEM discrete results for reference (color online)"

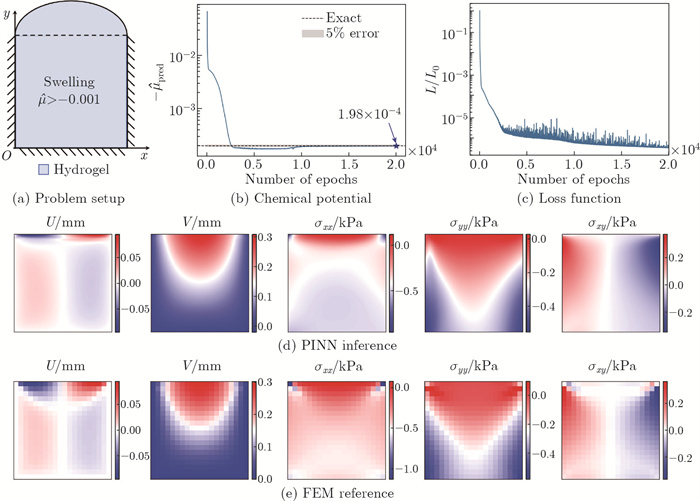
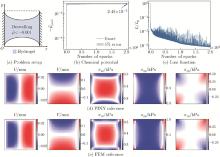
Fig. 7

Prediction results for the inverse problem of hydrogel deswelling under chemical potential stimuli: (a) the problem setup, with the left and right edges flxed; (b) the convergence history of the chemical potential , achieving a relative error of 0.87%; (c) the decreasing history of the loss function; (d) the continuous full-fleld solution output by the network; (e) the FEM discrete results for reference (color online)"

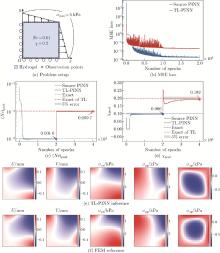
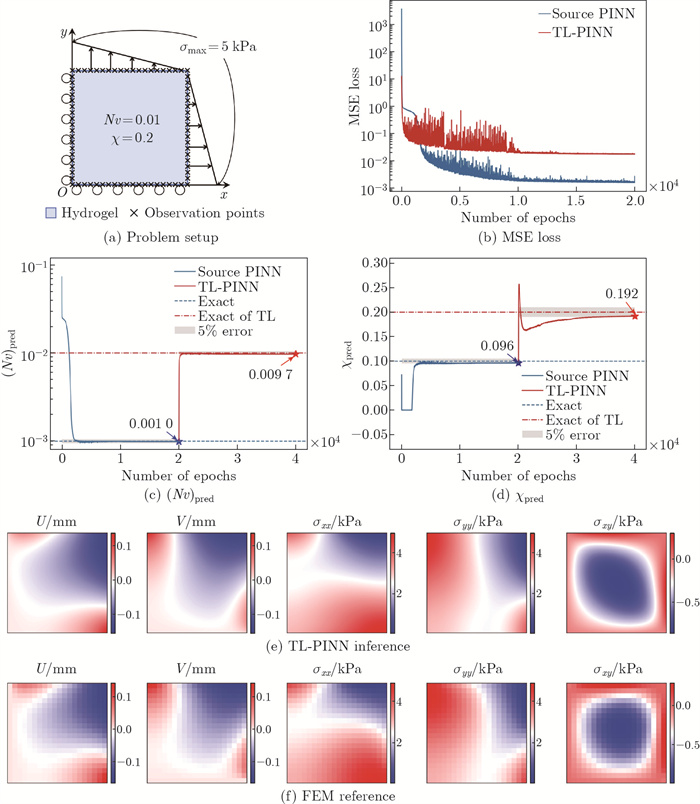
Fig. 8

The TL-PINN performance in parameter identiflcation and solution inference for hydrogel with multitask transfer learning: (a) the problem setup, similar to the inverse problem prototype for hydrogel but with a tenfold increase in Nv, a doubled χ, and a quintupled σmax; (b) the convergence of the total MSE loss for the source PINN and TL-PINN; (c) the convergence of the source PINN and TL-PINN for identifying Nv; (d) the convergence of the source PINN and TL-PINN for identifying χ; (e) the full-fleld predictions of flve mechanical quantities by the TL-PINN; (f) the FEM results for reference (color online)"

Table 1

Relative errors for the predicted values of the material parameters Nv and χ at difierent stages of training the source PINN and TL-PINN"

Fig. 9

Convergence of the MSE loss (L2 loss) for (a) the source model and (b) the TL-PINN model, where the same logarithmic y-axis is used for comparison (color online)"