Neural network solution based on the minimum potential energy principle for static problems of structural mechanics

doi:10.1007/s10483-025-3257-8

Abstract

Abstract:

This paper presents the variational physics-informed neural network (VPINN) as an effective tool for static structural analyses. One key innovation includes the construction of the neural network solution as an admissible function of the boundary-value problem (BVP), which satisfies all geometrical boundary conditions. We then prove that the admissible neural network solution also satisfies natural boundary conditions, and therefore all boundary conditions, when the stationarity condition of the variational principle is met. Numerical examples are presented to show the advantages and effectiveness of the VPINN in comparison with the physics-informed neural network (PINN). Another contribution of the work is the introduction of Gaussian approximation of the Dirac delta function, which significantly enhances the ability of neural networks to handle singularities, as demonstrated by the examples with concentrated support conditions and loadings. It is hoped that these structural examples are so convincing that engineers would adopt the VPINN method in their structural design practice.

Key words: physics-informed neural network (PINN), variational physics-informed neural network (VPINN), structural statics, admissible function, Gaussian approximation

2010 MSC Number:

O324

Jiamin QIAN, Lincong CHEN, J. Q. SUN. Neural network solution based on the minimum potential energy principle for static problems of structural mechanics. Applied Mathematics and Mechanics (English Edition), 2025, 46(6): 1125-1142.

TrendMD

Figures/Tables 18

Fig. 1

Table 1

Comparison of computational accuracy and training time between the VPINN and PINN methods for solving static responses of the cantilever beam with elastic supports"

Method	Iteration	Neural network structure	Sample	CPU time/s	$e L 1$
PINN	40	1-60-1	2 000	34.12	16.120
PINN	200	1-48-48-48-48-1	10 000	298.12	0.931
VPINN	40	1-60-1	2 000	11.25	0.354

Table 1

Table 2

Comparison of the moments and shear forces at discontinuous points of the cantilever beam with elastic supports computed by the VPINN and PINN with the FE solution. M1 is the moment to the left of the concentrated force, and M2 is the moment to the right of the concentrated force. V1 is the shear force to the left of the torsional spring, and V2 is the shear force to the right of the torsional spring"

Method	$M 1$ /( $N ⋅ m$ )	$M 2$ /( $N ⋅ m$ )	$V 1$ /N	$V 2$ /N
FE	176.91	$6.01 × 10 − 5$	1 000	$− 7.69 × 10 − 5$
PINN	165.66	$− 8.73$	979.73	$− 9.94$
VPINN	172.15	$− 1.40$	984.12	$− 2.25$
Method	$e M 1$ /%	$e M 2$ /%	$e V 1$ /%	$e V 2$ /%
PINN	6.36	8.73	2.03	9.94
VPINN	2.69	1.40	1.59	2.25
Note that $e$ represents the percentage error between the approximate and FE solutions

Table 2

Fig. 2

Fig. 3

Fig. 4

Fig. 5

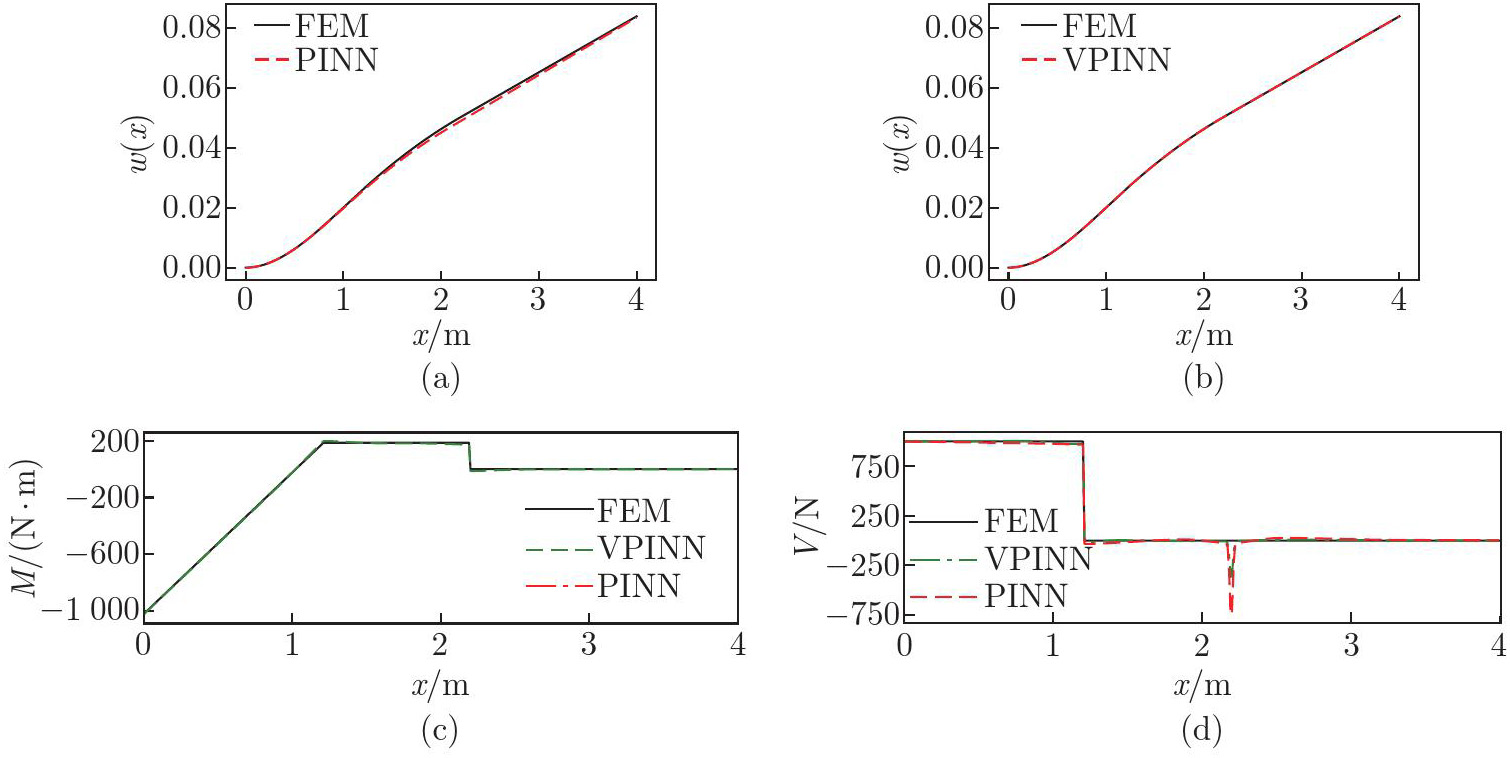
Table 3

Comparison of the solution accuracy and training steps of the VPINN and PINN methods for solving the responses of the cantilever Timoshenko beam with uniform loading"

Method	Iteration	Neural network structure	Sample	CPU time/s	$e L 1$
PINN	200	1-20-20-2	14 000	351.33	4.210 00
PINN	500	1-20-20-2	10 000	298.12	0.763 00
VPINN	200	1-20-20-2	14 000	78.00	0.004 12

Table 3

Table 4

Effect of activation functions of the VPINN on the responses of the cantilever Timoshenko beam"

Iteration	Neural network structure	Activation function	Sample	$e L 1$
200	1-20-20-2	sigmoid	14 000	0.052 40
200	1-20-20-2	ReLU	14 000	1.240 00
200	1-20-20-2	tanh	14 000	0.004 12

Table 4

Table 5

The moment M and shear force V of the beam at x=0"

Method	$M$ /(N·m)	$e M$	$V$ /N	$e V$
Analytical	$− 800.00$	0.000 00	$− 400.00$	0.000 0
PINN	$− 798.06$	0.242 00	$− 393.93$	1.500 0
VPINN	$− 802.14$	0.008 28	$− 405.14$	0.012 8

Table 5

Fig. 6

Fig. 7

Table 6

Comparison of L2 error and training time between the VPINN and PINN methods for solving the displacement fields of the thick-walled cylinder"

Method	Iteration	Neural network structure	CPU time/s	Sample	$e L 2$
PINN	100	2-10-10-2	130.07	3 600	0.037 340
PINN	100	2-20-20-20-2	682.14	3 600	0.079 880
VPINN	100	2-10-10-2	113.10	3 600	0.004 158

Table 6

Table 7

Influence of activation function types on the results of the VPINN method for solving displacements of the thick-walled cylinder"

VPINN iteration	Neural network structure	Activation function	Sample	$e L 2$
100	2-10-10-2	tanh	3 600	0.007 202
100	2-10-10-2	softmax	3 600	0.006 222
100	2-10-10-2	sigmoid	3 600	0.005 291

Table 7

Fig. 8

Fig. 9

Fig. 10

Table 8

Comparison of stresses and errors at x=0, y=1 and x=1, y=0 of the thick-walled cylinder"

Method	$σ r r, max$	$σ r r, min$	$σ θ θ, max$	$σ θ θ, min$	$σ r θ$
Analytical	11.33	-10.00	11.33	-10.00	0.000
VPINN	11.17	-10.18	11.67	$− 9.83$	0.221
PINN	11.97	-10.05	10.81	-10.12	0.207
Method	$e r r, max$	$e r r, min$	$e θ θ, max$	$e θ θ, min$	$e r θ$
VPINN	1.41	1.800	3.00	1.70	2.21
PINN	5.65	0.500	4.56	1.20	2.07

Table 8

References 31

[32]	SICK, B. On-line and indirect tool wear monitoring in turning with artificial neural networks: a review of more than a decade of research. Mechanical Systems and Signal Processing, 16(4), 487–546 (2002)
[33]	LI, Z., LIU, F., YANG, W., PENG, S., and ZHOU, J. A survey of convolutional neural networks: analysis, applications, and prospects. IEEE Transactions on Neural Networks and Learning Systems, 33(12), 6999–7019 (2021)
[34]	WANG, X., JIANG, J., HONG, L., and SUN, J. Q. Random vibration analysis with radial basis function neural networks. International Journal of Dynamics and Control, 10(5), 1385–1394 (2022)
[35]	QIAN, J., CHEN, L., and SUN, J. Q. Random vibration analysis of vibro-impact systems: RBF neural network method. International Journal of Non-Linear Mechanics, 148, 104261 (2023)
[36]	TIMOSHENKO, S. Theory of Elasticity, Oxford University Press, Oxford (1951)
[1]	RAISSI, M., PERDIKARIS, P., and KARNIADAKIS, G. E. Physics-informed neural networks: a deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. Journal of Computational Physics, 378, 686–707 (2019)
[2]	WU, L., NGUYEN, V. D., KILINGAR, N. G., and NOELS, L. A recurrent neural network-accelerated multi-scale model for elasto-plastic heterogeneous materials subjected to random cyclic and non-proportional loading paths. Computer Methods in Applied Mechanics and Engineering, 369, 113234 (2020)
[3]	CAI, S., MAO, Z., WANG, Z., YIN, M., and KARNIADAKIS, G. E. Physics-informed neural networks (PINNs) for fluid mechanics: a review. Acta Mechanica Sinica, 37(12), 1727–1738 (2021)
[4]	CHEN, Y., LU, L., KARNIADAKIS, G. E., and NEGRO, L. D. Physics-informed neural networks for inverse problems in nano-optics and metamaterials. Optics Express, 28(8), 11618–11633 (2020)
[5]	DANEKER, M., ZHANG, Z., KARNIADAKIS, G. E., and LU, L. Systems biology: identifiability analysis and parameter identification via systems-biology-informed neural networks. Computational Modeling of Signaling Networks (ed. NGUYEN, L. K.), Humana Press, New York, NY, 87–105 (2023)
[6]	JAGTAP, A. D., KHARAZMI, E., and KARNIADAKIS, G. E. Conservative physics-informed neural networks on discrete domains for conservation laws: applications to forward and inverse problems. Computer Methods in Applied Mechanics and Engineering, 365, 113028 (2020)
[7]	JAGTAP, A. D. and KARNIADAKIS, G. E. Extended physics-informed neural networks (XPINNs): a generalized space-time domain decomposition based deep learning framework for nonlinear partial differential equations. Communications in Computational Physics, 28(5), 2002–2041 (2020)
[8]	PANG, G., LU, L., and KARNIADAKIS, G. E. fPINNs: fractional physics-informed neural networks. SIAM Journal on Scientific Computing, 41(4), A2603–A2626 (2019)
[9]	LINKA, K., SCHÄFER, A., MENG, X., ZOU, Z., KARNIADAKIS, G. E., and KUHL, E. Bayesian physics informed neural networks for real-world nonlinear dynamical systems. Computer Methods in Applied Mechanics and Engineering, 402, 115346 (2022)
[10]	E, W. N. and YU, B. The deep Ritz method: a deep learning-based numerical algorithm for solving variational problems. Communications in Mathematics and Statistics, 6(1), 1–12 (2018)
[11]	KHARAZMI, E., ZHANG, Z., and KARNIADAKIS, G. E. hp-VPINNs: variational physics-informed neural networks with domain decomposition. Computer Methods in Applied Mechanics and Engineering, 374, 113547 (2021)
[12]	KHARAZMI, E., ZHANG, Z., and KARNIADAKIS, G. E. Variational physics-informed neural operator (VINO) for solving partial differential equations. Computer Methods in Applied Mechanics and Engineering, 437, 117785 (2025)
[13]	NGUYEN-THANH, V. M., ZHUANG, X., and RABCZUK, T. A deep energy method for finite deformation hyperelasticity. European Journal of Mechanics-A/Solids, 80, 103874 (2020)
[14]	SAMANIEGO, E., ANITESCU, C., GOSWAMI, S., NGUYEN-THANH, V. M., GUO, H., HAMDIA, K., ZHUANG, X., and RABCZUK, T. An energy approach to the solution of partial differential equations in computational mechanics via machine learning: concepts, implementation and applications. Computer Methods in Applied Mechanics and Engineering, 362, 112790 (2020)
[15]	NGUYEN-THANH, V. M., ANITESCU, C., ALAJLAN, N., RABCZUK, T., and ZHUANG, X. Parametric deep energy approach for elasticity accounting for strain gradient effects. Computer Methods in Applied Mechanics and Engineering, 386, 114096 (2021)
[16]	GOSWAMI, S., ANITESCU, C., and RABCZUK, T. Adaptive fourth-order phase field analysis using deep energy minimization. Theoretical and Applied Fracture Mechanics, 107, 102527 (2020)
[17]	GOSWAMI, S., ANITESCU, C., CHAKRABORTY, S., and RABCZUK, T. Transfer learning enhanced physics informed neural network for phase-field modeling of fracture. Theoretical and Applied Fracture Mechanics, 106, 102447 (2020)
[18]	GOSWAMI, S., YIN, M., YU, Y., and KARNIADAKIS, G. E. A physics-informed variational DeepONet for predicting crack path in quasi-brittle materials. Computer Methods in Applied Mechanics and Engineering, 391, 114587 (2022)
[19]	ABUEIDDA, D. W., KORIC, S., ABU AL-RUB, R., PARROTT, C. M., JAMES, K. A., and SOBH, N. A. A deep learning energy method for hyperelasticity and viscoelasticity. European Journal of Mechanics-A/Solids, 95, 104639 (2022)
[20]	HE, J., ABUEIDDA, D., ABU AL-RUB, R., KORIC, S., and JASIUK, I. A deep learning energy-based method for classical elastoplasticity. International Journal of Plasticity, 162, 103531 (2023)
[21]	FUHG, J. N. and BOUKLAS, N. The mixed deep energy method for resolving concentration features in finite strain hyperelasticity. Journal of Computational Physics, 451, 110839 (2022)
[22]	REZAEI, S., HARANDI, A., MOEINEDDIN, A., XU, B. X., and REESE, S. A mixed formulation for physics-informed neural networks as a potential solver for engineering problems in heterogeneous domains: comparison with finite element method. Computer Methods in Applied Mechanics and Engineering, 401, 115616 (2022)
[23]	WANG, Y., SUN, J., RABCZUK, T., and LIU, Y. CENN: conservative energy method based on neural networks with subdomains for solving variational problems involving heterogeneous and complex geometries. Computer Methods in Applied Mechanics and Engineering, 400, 115491 (2022)
[24]	LI, W., BAZANT, M. Z., and ZHU, J. A physics-guided neural network framework for elastic plates: comparison of governing equations-based and energy-based approaches. Computer Methods in Applied Mechanics and Engineering, 383, 113933 (2021)
[25]	BASTEK, J. H. and KOCHMANN, D. M. Physics-informed neural networks for shell structures. European Journal of Mechanics-A/Solids, 97, 104849 (2023)
[26]	CHEN, Z., BADRINARAYANAN, V., LEE, C. Y., and RABINOVICH, A. GradNorm: gradient normalization for adaptive loss balancing in deep multitask networks. Proceedings of the Machine Learning Research, 80, 794–803 (2018)
[27]	WANG, S., YU, X., and PERDIKARIS, P. When and why PINNs fail to train: a neural tangent kernel perspective. Journal of Computational Physics, 449, 110768 (2022)
[28]	WANG, S., TENG, Y., and PERDIKARIS, P. Understanding and mitigating gradient flow pathologies in physics-informed neural networks. SIAM Journal on Scientific Computing, 43(5), A3055–A3081 (2021)
[29]	HAGHIGHAT, E., AMINI, D., and JUANES, R. Physics-informed neural network simulation of multiphase poroelasticity using stress-split sequential training. Computer Methods in Applied Mechanics and Engineering, 397, 115141 (2022)
[30]	MEIROVITCH, L. Analytical Methods in Vibrations, Macmillan, London (1967)
[31]	NAIR, V. and HINTON, G. E. Rectified linear units improve restricted Boltzmann machines. Proceedings of the 27th International Conference on Machine Learning, Omnipress, Boston, MA, 807–814 (2010)