Applied Mathematics and Mechanics (English Edition) ›› 2025, Vol. 46 ›› Issue (12): 2241-2264.doi: https://doi.org/10.1007/s10483-025-3325-8
Previous Articles Next Articles
Lingjun MENG, Xiuting SUN†( ), Jian XU
), Jian XU
Received:2025-06-26
Revised:2025-09-28
Published:2025-11-28
Contact:
Xiuting SUN, E-mail: 05mech_sunxiuting@tongji.edu.cnSupported by:2010 MSC Number:
Lingjun MENG, Xiuting SUN, Jian XU. A novel multi-dimensional isolation platform for low-frequency excitations: analysis and experiment. Applied Mathematics and Mechanics (English Edition), 2025, 46(12): 2241-2264.
Fig. 2
The assembly process for realizing the WA-HSLDS property with sufficient load-carrying capacity and the corresponding restoring force variation in one origami-based sub-leg: (a) the corresponding restoring forces for linear spring FR(L); (b) the sum of the restoring force FR(s) for the OCS; (c) the PSA design of OCS and linear spring for the WA-HSLDS property (color online)"
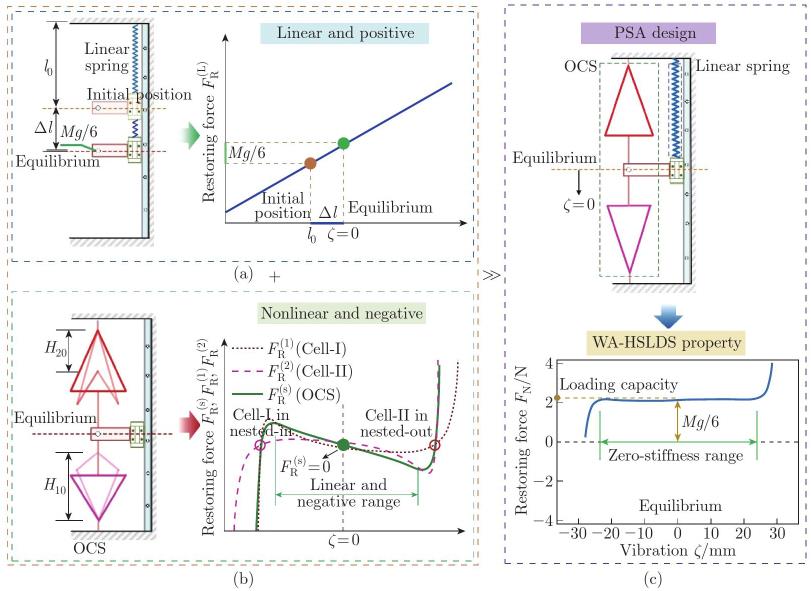
Fig. 3
The simplified mechanical diagrams of the proposed 6-D VI platform for 6-D base excitations: (a) the static equilibrium and the coordinate systems; (b) the associated structural parameters; (c) an arbitrary posture of the upper platform and the closed-loop vectors of motions (color online)"
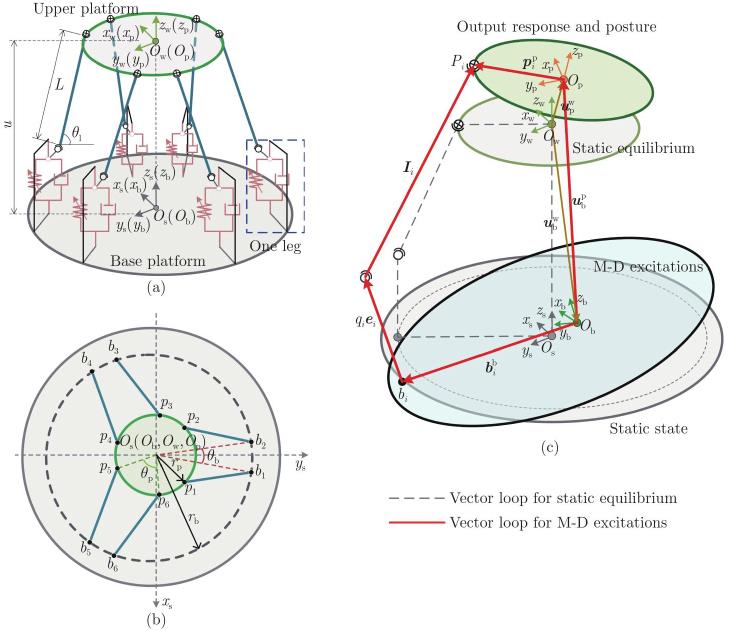
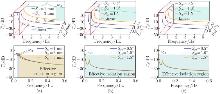
Fig. 7
The VI performances for different values of the excitation amplitudes Si0 in D-M: (a) the z-dimensional displacement transmissibility for increasing Sz0; (b) the α-dimensional displacement transmissibility for increasing Sα0; (c) the β-dimensional displacement transmissibility for increasing Sβ0 (color online)"
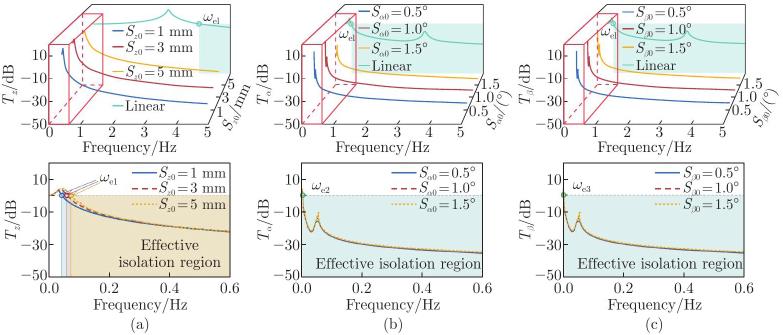

Fig. 9
The experimental prototype of the proposed M-D VI platform for 6-D excitations induced by a six-DOF excitation simulator: (a) the detailed experimental analysis and processes; (b) the construction of experimental prototype; (c) the construction of one origami-based sub-leg with PSA of origami and spring; (d) load-carrying capacity and equivalent restoring force in the z-direction; (e) dynamic testing environment for 6-D excitations by a six-DOF excitation simulator (color online)"
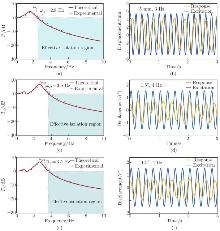
Fig. 10
The VI performances of the proposed platform under S-D excitations: (a) the displacement transmissibility diagram under the z-dimensional excitation; (b) the time-domain diagram at 3 Hz under the z-dimensional excitation; (c) the displacement transmissibility diagram under the α-dimensional excitation; (d) the time-domain diagram at 4 Hz under the α-dimensional excitation; (e) the displacement transmissibility diagram under the β-dimensional excitation; (f) the time-domain diagram at 4 Hz under the β-dimensional excitation (color online)"

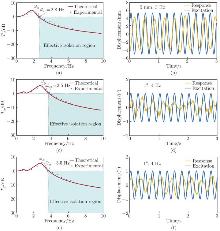
Fig. 11
The VI performances of the proposed platform under M-D excitations: (a) the displacement transmissibility diagram under the z-dimensional excitation; (b) the time-domain diagram at 3 Hz under the z-dimensional excitation; (c) the displacement transmissibility diagram under the α-dimensional excitation; (d) the time-domain diagram at 4 Hz under the α-dimensional excitation; (e) the displacement transmissibility diagram under the β-dimensional excitation; (f) the time-domain diagram at 4 Hz under the β-dimensional excitation (color online)"
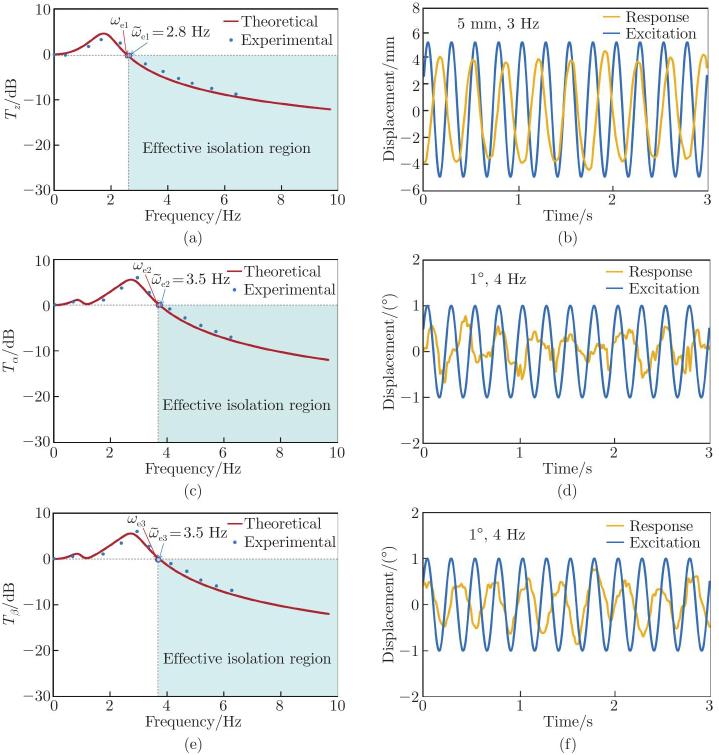
Table 1
A summary of representative M-D VI platforms"
| Reference | Platform configuration | Superiority | Loading | Leg weight | Isolation region | ||
|---|---|---|---|---|---|---|---|
| Ou et al.[ | SGP based-metamaterial structures | Multi-payloads VI utilizing metamaterial structure | 1.05 kg | Lightweight | 10 Hz | 3.9 Hz | 3.9 Hz |
| Wu et al.[ | SGP based-bio-inspired X-shape structures | Applying X-shape structure | About 4 kg | 6 Hz | 7 Hz | ||
| Present | Novel platform based-origami structures | Novel configuration designed based on origami and parallel mechanism; decoupled structural design | 1.2 kg | Lightweight | 2.8 Hz | 3.5 Hz | 3.5 Hz |
| [3] | WANG, W., NING, Y., ZHANG, Y., XU, P., and LI, B. Linear active disturbance rejection control with linear quadratic regulator for Stewart platform in active wave compensation system. Applied Ocean Research, 156, 104469 (2025) |
| [4] | YUN, H., LIU, L., LI, Q., LI, W., and TANG, L. Development of an isotropic Stewart platform for telescope secondary mirror. Mechanical Systems and Signal Processing, 127, 328–344 (2019) |
| [5] | CHEN, D., ZI, H., LI, Y., and LI, X. Low frequency ship vibration isolation using the band gap concept of sandwich plate-type elastic metastructures. Ocean Engineering, 235, 109460 (2021) |
| [6] | CHEN, S., XUAN, M., XIN, J., LIU, Y., GU, S., LI, J., and ZHANG, L. Design and experiment of dual micro-vibration isolation system for optical satellite flywheel. International Journal of Mechanical Sciences, 179, 105592 (2020) |
| [7] | BAI, J., YE, T., JIN, G., CHEN, Y., LI, W., and YUAN, J. Theoretical and experimental investigation of a two-stage X-structure vibration isolation system with inerter coupling for marine equipment. Ocean Engineering, 323, 120351 (2025) |
| [8] | CHAI, Y., BIAN, J., and LI, M. A novel quasi-zero-stiffness isolation platform via tunable positive and negative stiffness compensation mechanism. Nonlinear Dynamics, 112, 101–123 (2023) |
| [9] | HU, B. and ZHANG, J. The terminal constraint and coupling kinematics of a novel 3-UPU parallel mechanism with screw type terminal constraints. Mechanism and Machine Theory, 210, 106018 (2025) |
| [10] | YIN, R., XIE, W., WEN, Y., ZHANG, C., CHEN, W., and ZHANG, W. Robust wave compensation controller design for an active hexapod platform with time-varying input delays. Ocean Engineering, 274, 114084 (2023) |
| [11] | CHEN, W., WANG, S., LI, J., LIN, C., YANG, Y., REN, A., LI, W., ZHAO, X., ZHANG, W., GUO, W., and GAO, F. An ADRC-based triple-loop control strategy of ship-mounted Stewart platform for six-DOF wave compensation, Mechanism and Machine Theory, 184, 105289 (2023) |
| [12] | RAN, L., WANG, J., HALIM, D., SHI, B., and HUANG, L. A semi-active quasi-zero-stiffness vibration isolation system through controllable lateral spring stiffness. Nonlinear Dynamics, 112, 13751–13770 (2024) |
| [13] | LUO, C., ZHU, Z., GUO, Y., WANG, J., and JING, X. Multi-direction vibration isolation with tunable QZS performance via novel X-mechanism design. Communications in Nonlinear Science and Numerical Simulation, 137, 108140 (2024) |
| [14] | CHAI, Y., JING, X., and CHAO, X. X-shaped mechanism based enhanced tunable QZS property for passive vibration isolation. International Journal of Mechanical Sciences, 218, 107077 (2022) |
| [15] | LIU, C., JING, X., DALEY, S., and LI, F. Recent advances in micro-vibration isolation. Mechanical Systems and Signal Processing, 56-57, 55–80 (2015) |
| [16] | XIAO, H., ZHU, Z., QIE, H., LIANG, G., TANG, Y., BOWEN, C., and ROSCOW, J. Modelling and performance enhancement of the fluid coupling interface for hydraulic pressure energy harvesting by superposition of the static mean pressure and pressure fluctuations. Mechanical Systems and Signal Processing, 224, 112042 (2025) |
| [17] | PAN, W., XIE, H., AI, P., LIU, R., GAO, B., XIE, S., LUO, Y., and ZHANG, Y. A novel large linear stroke high-static-low-dynamic stiffness vibration isolator with high magnetic negative stiffness and compactness. Engineering Structures, 331, 120014 (2025) |
| [18] | YAN, B., YU, N., MA, H., and WU, C. A theory for bistable vibration isolators. Mechanical Systems and Signal Processing, 167, 108507 (2022) |
| [19] | HAO, R., LU, Z., DING, H., and CHEN, L. A nonlinear vibration isolator supported on a flexible plate: analysis and experiment. Nonlinear Dynamics, 108, 941–958 (2022) |
| [20] | XU, Y., DONG, H., and WANG, Y. Topology optimization of programable quasi-zero-stiffness metastructures for low-frequency vibration isolation. International Journal of Mechanical Sciences, 280, 109557 (2024) |
| [21] | PEI, L., CHONG, A. S. E., PAVLOVSKAIA, E., and WIERCIGROCH, M. Computation of periodic orbits for piecewise linear oscillator by harmonic balance methods. Communications in Nonlinear Science and Numerical Simulation, 108, 106220 (2022) |
| [22] | ZENG, R., YIN, S., WEN, G., and ZHOU, J. A non-smooth quasi-zero-stiffness isolator with displacement constraints. International Journal of Mechanical Sciences, 225, 107351 (2022) |
| [23] | WEN, G., LIN, Y., and HE, J. A quasi-zero-stiffness isolator with a shear-thinning viscous damper. Applied Mathematics and Mechanics (English Edition), 43(3), 311–326 (2022) https://doi.org/10.1007/s10483-022-2829-9 |
| [24] | PAN, G., JIAO, X., LIN, C., GUAN, Z., WU, J., LIU, H., ZHAO, H., and HUANG, H. High load-bearing quasi-zero stiffness metamaterials for vibration isolation. International Journal of Mechanical Sciences, 293, 110225 (2025) |
| [25] | ZHOU, J., ZHOU, J., PAN, H., WANG, K., CAI, C., and WEN, G. Multi-layer quasi-zero-stiffness meta-structure for high-efficiency vibration isolation at low frequency. Applied Mathematics and Mechanics (English Edition), 45(7), 1189–1208 (2024) https://doi.org/10.1007/s10483-024-3157-6 |
| [26] | WANG, J. and YAO, G. Multi-directional vibration isolation performances of a scissor-like structure with nonlinear hybrid spring stiffness. Nonlinear Dynamics, 112, 8871–8888 (2024) |
| [27] | WANG, J. and YAO, G. A 3-DOF frog-inspired quasi-zero stiffness isolator and its vibration control performance. Aerospace Science and Technology, 149, 109163 (2024) |
| [28] | OU, H., SUN, X., WU, Q., CHEN, Z., CHEN, Z., CHEN, Q., and HU, L. A novel bio-inspired kangaroo leg structure for low-frequency vibration isolation. Nonlinear Dynamics, 112, 1797–1814 (2023) |
| [29] | JING, X. The X-structure/mechanism approach to beneficial nonlinear design in engineering. Applied Mathematics and Mechanics (English Edition), 43(7), 979–1000 (2022) https://doi.org/10.1007/s10483-022-2862-6 |
| [30] | CHEN, H., ZENG, Y., DING, H., LAI, S., and CHEN, L. Dynamics and vibration reduction performance of asymmetric tristable nonlinear energy sink. Applied Mathematics and Mechanics (English Edition), 45(3), 389–406 (2024) https://doi.org/10.1007/s10483-024-3095-9 |
| [31] | ZHAO, F., JI, J., YE, K., and LUO, Q. An innovative quasi-zero stiffness isolator with three pairs of oblique springs. International Journal of Mechanical Sciences, 192, 106093 (2021) |
| [32] | LU, Z., HAO, R., WU, D., DING, H., and CHEN, L. An investigation of a self-powered low-frequency nonlinear vibration isolation system. Engineering Structures, 315, 118395 (2024) |
| [33] | YU, N., YANG, K., WU, Z., ZHANG, W., and YAN, B. Low-frequency vibration absorption of magnetic quasi-zero-stiffness structures with lever mechanism. International Journal of Mechanical Sciences, 267, 108973 (2024) |
| [34] | LIU, J., WANG, Y., YANG, S., SUN, T., YANG, M., and NIU, W. Customized quasi-zero-stiffness metamaterials for ultra-low frequency broadband vibration isolation. International Journal of Mechanical Sciences, 269, 108958 (2024) |
| [35] | MA, H., WANG, K., ZHAO, H., ZHAO, C., XUE, J., LIANG, C., and YAN, B. Harnessing chiral buckling structure to design tunable local resonance metamaterial for low-frequency vibration isolation. Journal of Sound and Vibration, 565, 117905 (2023) |
| [36] | LI, M., CHENG, W., and XIE, R. A quasi-zero-stiffness vibration isolator using a cam mechanism with user-defined profile. International Journal of Mechanical Sciences, 189, 105938 (2021) |
| [37] | MAO, X., YIN, M., DING, H., GENG, X., SHEN, Y., and CHEN, L. Modeling, analysis, and simulation of X-shape quasi-zero-stiffness-roller vibration isolators. Applied Mathematics and Mechanics (English Edition), 43(7), 1027–1044 (2022) https://doi.org/10.1007/s10483-022-2871-6 |
| [38] | XIA, S., LI, Y., WEN, G., XU, D., WANG, K., and ZHANG, H. Natural mechanism of superexcellent vibration isolation of the chicken neck. Journal of Sound and Vibration, 594, 118649 (2025) |
| [39] | ZHOU, W., LI, Y., ZHOU, J., and PENG, Y. Limb-inspired quasi-zero stiffness structure for ultralow-frequency vibration attenuation, International Journal of Mechanical Sciences, 274, 109251 (2024) |
| [40] | XU, K., NIU, M., ZHANG, Y., and CHEN, L. An active high-static-low-dynamic-stiffness vibration isolator with adjustable buckling beams: theory and experiment. Applied Mathematics and Mechanics (English Edition), 45(3), 425–440 (2024) https://doi.org/10.1007/s10483-024-3087-6 |
| [41] | LIU, C., ZHAO, R., YU, K., LEE, H., and LIAO, B. A quasi-zero-stiffness device capable of vibration isolation and energy harvesting using piezoelectric buckled beams. Energy, 233, 121146 (2021) |
| [42] | DAI, H., JING, X., WANG, Y., YUE, X., and YUAN, J. Post-capture vibration suppression of spacecraft via a bio-inspired isolation system. Mechanical Systems and Signal Processing, 105, 214–240 (2018) |
| [43] | CHAI, Y. and JING, X. Low-frequency multi-direction vibration isolation via a new arrangement of the X-shaped linkage mechanism. Nonlinear Dynamics, 109, 2383–2421 (2022) |
| [44] | LU, Z., WU, D., DING, H., and CHEN, L. Vibration isolation and energy harvesting integrated in a Stewart platform with high static and low dynamic stiffness. Applied Mathematical Modelling, 89, 249–267 (2021) |
| [45] | HAO, R., LU, Z., DING, H., and CHEN, L. Orthogonal six-DOFs vibration isolation with tunable high-static-low-dynamic stiffness: experiment and analysis. International Journal of Mechanical Sciences, 222, 107237 (2022) |
| [46] | SUN, K., TANG, J., WU, Z., LI, Y., and CAO, D. Coupled nonlinear vibration characteristics of quasi-zero-stiffness Gough-Stewart isolation platform. Aerospace Science and Technology, 152, 109352 (2024) |
| [47] | OU, H., ZENG, J., LIN, M., WANG, Y., ZENG, Y., FANG, X., and HU, L. Stair-stepping metamaterial and the derived isolator for all-DOF vibrations with multi-payloads. Engineering Structures, 330, 119890 (2025) |
| [48] | WU, Z., JING, X., SUN, B., and LI, F. A 6DOF passive vibration isolator using X-shape supporting structures. Journal of Sound and Vibration, 380, 90–111 (2016) |
| [49] | WANG, M., HU, Y., SUN, Y., DING, J., PU, H., YUAN, S., ZHAO, J., PENG, Y., XIE, S., and LUO, J. An adjustable low-frequency vibration isolation Stewart platform based on electromagnetic negative stiffness. International Journal of Mechanical Sciences, 181, 105714 (2020) |
| [50] | ZENG, Y., DING, H., and JI, J. An origami-inspired nonlinear energy sink: design, modeling, and analysis. Applied Mathematics and Mechanics (English Edition), 46(4), 601–616 (2025) https://doi.org/10.1007/s10483-025-3239-6 |
| [51] | LIU, J., PANG, Z., LI, Z., WEN, G., SU, Z., HE, J., LIU, K., JIANG, D., LI, Z., CHEN, S., TIAN, Y., XIE, Y., WANG, Z., and LIU, Z. An origami-wheeled robot with variable width and enhanced sand walking versatility. Thin-Walled Structures, 206, 112645 (2025) |
| [52] | LEE, T. U., LU, H. J., MA, J. M., HA, N. S., GATTAS, J. M., and XIE, Y. M. Self-locking and stiffening deployable tubular structures. Proceedings of the National Academy of Sciences of the United States of America, 121(40), e2409062121 (2024) |
| [53] | WANG, X., QU, H., and GUO, S. Tristable property and the high stiffness analysis of Kresling pattern origami. International Journal of Mechanical Sciences, 256, 108515 (2023) |
| [1] | WANG, Y., ZHANG, P., LU, X., GAO, Y., and CHEN, Y. A multi-target and multi-state control method for cable-rigid coupled wave motion compensation devices. Ocean Engineering, 316, 119895 (2025) |
| [2] | ZHU, B., LI, E., ZHAO, T., WANG, C., TANG, Z., and LI, Z. Dynamic characteristics of series-parallel hybrid rigid-flexible coupling double-mass underactuated system on floating platform. Mechanism and Machine Theory, 179, 105132 (2023) |
| [54] | LIU, S., PENG, G., and JIN, K. Design and characteristics of a novel QZS vibration isolation system with origami-inspired corrector. Nonlinear Dynamics, 106, 255–277 (2021) |
| [55] | SUN, X., LV, Q., QIAN, J., and XU, J. Vibration isolation platform for large-amplitude-low-frequency excitation by parallel-stack-assembly design of Miura origamis. International Journal of Non-Linear Mechanics, 166, 104831 (2024) |
| [56] | HAN, H., TANG, L., WU, J., SUN, S., YIN, P., and CAO, D. Origami-inspired isolators with quasi-zero stiffness for coupled axial-torsional vibration. Aerospace Science and Technology, 140, 108438 (2023) |
| [57] | LIN, C., XIN, B., WANG, S., ZHOU, S., CHEN, W., and GAO, F. Dynamic characteristics analysis and multi-source disturbances rejection control of a 6-PUS parallel stabilization mechanism on floating base. Mechanism and Machine Theory, 205, 105888 (2025) |
| [58] | TANG, G., LEI, J., LI, F., ZHU, W., XU, X., YAO, B., CLARAMUNT, C., and HU, X. A modified 6-DOF hybrid serial–parallel platform for ship wave compensation. Ocean Engineering, 280, 114336 (2023) |
| [59] | HU, Y., QIAN, Q., LI, L., HU, X., LI, G., and MEI, X. A method for the kinematic analysis of a novel wave compensation bed for ships based on the 8PSS-UP parallel platform. Ocean Engineering, 288, 116120 (2023) |
| [60] | LIU, X., ZHAO, T., LUO, E., CHEN, W., and PAN, Q. Coupling 3-PSR/PSU 5-axis compensation mechanism for stabilized platform and its analysis. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 227, 1619–1629 (2013) |
| [61] | LI, S., FANG, H., SADEGHI, S., BHOVAD, P., and WANG, K. W. Architected origami materials: how folding creates sophisticated mechanical properties. Advanced Materials, 31, 1805282 (2018). |
| [62] | ZHOU, Y., ZHANG, Y., FENG, J., and CAI, J. Numerical study of the hysteretic behavior of energy dissipation braces based on Miura origami. International Journal of Non-Linear Mechanics, 157, 104523 (2023) |
| [1] | Hui MA, Hong GUAN, Lin QU, Xumin GUO, Qinqin MU, Yao ZENG, Yanyan CHEN. Dynamic modeling and simulation of blade-casing system with rubbing considering time-varying stiffness and mass of casing [J]. Applied Mathematics and Mechanics (English Edition), 2025, 46(5): 849-868. |
| [2] | Yu ZHOU, Li WANG, Jianliang HUANG. Periodic response and stability analysis of vibro-impact systems by an enriched harmonic balance method [J]. Applied Mathematics and Mechanics (English Edition), 2025, 46(5): 907-926. |
| [3] | Youcheng ZENG, Hu DING, J. C. JI. An origami-inspired nonlinear energy sink: design, modeling, and analysis [J]. Applied Mathematics and Mechanics (English Edition), 2025, 46(4): 601-616. |
| [4] | Kai LI, Chongfeng ZHAO, Yunlong QIU, Yuntong DAI. Light-powered self-rolling of a liquid crystal elastomer-based dicycle [J]. Applied Mathematics and Mechanics (English Edition), 2025, 46(2): 253-268. |
| [5] | S. SAURABH, R. KIRAN, D. SINGH, R. VAISH, V. S. CHAUHAN. A comprehensive investigation on nonlinear vibration andbending characteristics of bio-inspired helicoidallaminated composite structures [J]. Applied Mathematics and Mechanics (English Edition), 2025, 46(1): 81-100. |
| [6] | Canchang LIU, Qian DING, Qingmei GONG, Chicheng MA, Shuchang YUE. Axial control for nonlinear resonances of electrostatically actuated nanobeam with graphene sensor [J]. Applied Mathematics and Mechanics (English Edition), 2017, 38(4): 527-542. |
| [7] | R. NAZEMNEZHAD, P. FAHIMI. Free torsional vibration of cracked nanobeams incorporating surface energy effects [J]. Applied Mathematics and Mechanics (English Edition), 2017, 38(2): 217-230. |
| [8] | Lei HOU, Yushu CHEN. Bifurcation analysis of aero-engine's rotor system under constant maneuver load [J]. Applied Mathematics and Mechanics (English Edition), 2015, 36(11): 1417-1426. |
| [9] | Xiaodong WANG, Yushu CHEN, Lei HOU. Nonlinear dynamic singularity analysis of two interconnected synchronous generator system with 1:3 internal resonance and parametric principal resonance [J]. Applied Mathematics and Mechanics (English Edition), 2015, 36(8): 985-1004. |
| [10] | Demin ZHAO, Jianlin LIU, C. Q. WU. Stability and local bifurcation of parameter-excited vibration of pipes conveying pulsating fluid under thermal loading [J]. Applied Mathematics and Mechanics (English Edition), 2015, 36(8): 1017-1032. |
| [11] | A. G. ARANI, G. S. JAFARI. Nonlinear vibration analysis of laminated composite Mindlin micro/nano-plates resting on orthotropic Pasternak medium using DQM [J]. Applied Mathematics and Mechanics (English Edition), 2015, 36(8): 1033-1044. |
| [12] | Xuan XIE;Lingcheng KONG;Yuxi WANG;Jun ZHANG;Yuantai HU. Coupled vibrations and frequency shift of compound system consisting of quartz crystal resonator in thickness-shear motions and micro-beam array immersed in liquid [J]. Applied Mathematics and Mechanics (English Edition), 2015, 36(2): 225-232. |
| [13] | B. AMIRIAN;R. HOSSEINI-ARA;H. MOOSAVI. Surface and thermal effects on vibration of embedded alumina nanobeams based on novel Timoshenko beam model [J]. Applied Mathematics and Mechanics (English Edition), 2014, 35(7): 875-886. |
| [14] | Yu-li MA;Ji-wei CHEN;Yong-quan LIU;Xian-yue SU. Vibration analysis of foam plates based on cell volume distribution [J]. Applied Mathematics and Mechanics (English Edition), 2012, 33(12): 1493-1504. |
| [15] | Feng-ming LI;Chun-chuan LIU . Parametric vibration stability and active control of nonlinear beams [J]. Applied Mathematics and Mechanics (English Edition), 2012, 33(11): 1381-1392. |
| Viewed | ||||||
|
Full text |
|
|||||
|
Abstract |
|
|||||


 Email Alert
Email Alert RSS
RSS