Applied Mathematics and Mechanics (English Edition) ›› 2025, Vol. 46 ›› Issue (4): 601-616.doi: https://doi.org/10.1007/s10483-025-3239-6
Youcheng ZENG1,2, Hu DING1,3,4,†( ), J. C. JI2
), J. C. JI2
Received:2024-12-06
Revised:2025-02-11
Online:2025-04-07
Published:2025-04-07
Contact:
Hu DING, E-mail: dinghu3@shu.edu.cnSupported by:2010 MSC Number:
Youcheng ZENG, Hu DING, J. C. JI. An origami-inspired nonlinear energy sink: design, modeling, and analysis. Applied Mathematics and Mechanics (English Edition), 2025, 46(4): 601-616.

Fig. 8
The amplitude-frequency responses of the LO under different parameters: (a) θA0=−30π/180, kC=0.122 N/(rad·m), F0=2 N, m1=20 kg, G=0.514 5 N, and ε=0.262 5%; (b) θA0=−40π/180, kC=0.296 N/(rad·m), F0=2 N, m1=20 kg, G=1.366 N, and ε=0.696 9%; (c) θA0=−70π/180, kC=1.387 N/(rad·m), F0=2 N, m1=20 kg, G=10.21 N, and ε=5.209 2%. (d) Vibration reduction efficiency with different initial angles θA0 when m1=20 and F0=2 N(color online)"


Fig. 9
Displacement of the LO (left), displacement of the SMO-NES (middle), and spectrum of the SMO-NES (right) for (a)–(c) θA0=−30π/180, kC=0.122 N/(rad⋅m), G=0.514 5 N; (d)–(f) θA0=−40π/180, kC=0.296 N/(rad⋅m), G=1.366 N, F0=2 N, and ω=27.27 rad/s; (g)–(i) θA0=−70π/180, kC=1.387 N/(rad⋅m), G=10.21 N, F0=2 N, and ω=27.31 rad/s (color online)"


Fig. 11
Amplitude-frequency responses when (a) θA0=−30π/180, kC=0.122 N/(rad⋅m), F0=2.5 N, m1=20 kg, G=0.514 5 N, and ε=0.262 5%; (b) θA0=−40π/180, kC=0.296 N/(rad⋅m), F0=2.5 N, m1=20 kg, G=1.366 N, and ε=0.696 9%; (c) θA0=−50π/180, kC=0.538 N/(rad⋅m), F0=2.5 N, m1=20 kg, G=2.932 N, and ε=1.495 9%. (d) Vibration reduction efficiency and mass ratio with different initial angle θA0 when m1=20 kg and F0=2.5 N (color online)"

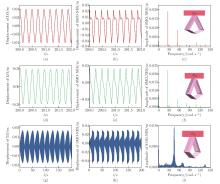
Fig. 12
Displacement of the LO (left), displacement of the SMO-NES (middle), and spectrum of the SMO-NES (right) for (a)–(c) θA0=−30π/180, kC=0.122 N/(rad⋅m), G=0.514 5 N, F0=2.5 N, and ω=27.22 rad/s; (d)–(f) θA0=−40π/180, kC=0.296 N/(rad⋅m), G=1.366 N, F0=2.5 N, and ω=27.06 rad/s; (g)–(i) θA0=−50π/180, kC=0.538 N/(rad⋅m), G=2.932 N, F0=2.5 N, and ω=27.27 rad/s (color online)"

| [1] | CHILLEMI, M., FURTMÜLLER, T., ADAM, C., and PIRROTTA, A. Fluid inerter-based vibration control of multi-modal structures subjected to vertical vibration. Engineering Structures, 307, 117938 (2024) |
| [2] | LIU, C. C., JING, X. J., DALEY, S., and LI, F. M. Recent advances in micro-vibration isolation. Mechanical Systems and Signal Processing, 56-57, 55–80 (2015) |
| [3] | GUZMAN PUJOLS, J. C. and RYAN, K. L. Computational simulation of slab vibration and horizontal-vertical coupling in a full-scale test bed subjected to 3D shaking at E-Defense. Earthquake Engineering & Structural Dynamics, 47(2), 438–459 (2017) |
| [4] | TOWARD, M. G. R. and GRIFFIN, M. J. The transmission of vertical vibration through seats: influence of the characteristics of the human body. Journal of Sound and Vibration, 330(26), 6526–6543 (2011) |
| [5] | ZHU, Y. N., GUO, X. Y., WANG, Q., and CAO, D. X. A lightweight tuned particle damper for low-frequency vibration attenuation. Journal of Sound and Vibration, 583, 118440 (2024) |
| [6] | ABÉ, M. and FUJINO, Y. Dynamic characterization of multiple tuned mass dampers and some design formulas. Earthquake Engineering & Structural Dynamics, 23(8), 813–835 (2007) |
| [7] | ZHANG, Y. F., KONG, X. R., YUE, C. F., and GUO, J. S. Characteristic analysis and design of nonlinear energy sink with cubic damping considering frequency detuning. Nonlinear Dynamics, 111(17), 15817–15836 (2023) |
| [8] | VAKAKIS, A. F., MANEVITCH, L. I., GENDELMAN, O., and BERGMAN, L. Dynamics of linear discrete systems connected to local, essentially non-linear attachments. Journal of Sound and Vibration, 264(3), 559–577 (2003) |
| [9] | LI, M., LI, S. B., and DING, H. Analysis of damping efficiency of nonlinear energy sink cell(in Chinese). Chinese Journal of Theoretical and Applied Mechanics, 55(11), 2614–2623 (2023) |
| [10] | CAO, Y. B., YAO, H. L., HAN, J. C., LI, Z. A., and WEN, B. C. Application of non-smooth NES in vibration suppression of rotor-blade systems. Applied Mathematical Modelling, 87, 351–371 (2020) |
| [11] | GAO, Q. Y. and YANG, T. Z. A nonlinear vibration isolator with an essentially nonlinear converter. Applied Mathematical Modelling, 136, 115648 (2024) |
| [12] | LI, W. K., WANG, Z. M., BRENNAN, M. J., and YANG, T. J. Design and optimization of a two-degrees-of-freedom single-sided vibro-impact nonlinear energy sink for transient vibration suppression of a thin plate. Journal of Sound and Vibration, 587, 118512 (2024) |
| [13] | LIAO, X., CHEN, L., ZHOU, S., and ZHANG, M. L. A novel vari-potential bistable nonlinear energy sink for improved vibration suppression: numerical and experimental study. Nonlinear Dynamics, 111(21), 19763–19790 (2023) |
| [14] | DOU, J. X., YAO, H. L., LI, H., LI, J. L., and JIA, R. Y. A track nonlinear energy sink with restricted motion for rotor systems. International Journal of Mechanical Sciences, 259, 108631 (2023) |
| [15] | LI, S. B., ZHOU, X. X., and CHEN, J. E. Hamiltonian dynamics and targeted energy transfer of a grounded bistable nonlinear energy sink. Communications in Nonlinear Science and Numerical Simulation, 117, 106898 (2023) |
| [16] | MA, K., DU, J. T., LIU, Y., and CHEN, X. M. Torsional vibration attenuation of a closed-loop engine crankshaft system via the tuned mass damper and nonlinear energy sink under multiple operating conditions. Mechanical Systems and Signal Processing, 207, 110941 (2024) |
| [17] | DING, H. and CHEN, L. Q. Designs, analysis, and applications of nonlinear energy sinks. Nonlinear Dynamics, 100(4), 3061–3107 (2020) |
| [18] | WANG, J. J. and ZHENG, Y. Q. Development and robustness investigation of track-based asymmetric nonlinear energy sink for impulsive response mitigation. Engineering Structures, 286, 116127 (2023) |
| [19] | WANG, Y., WANG, P. L., MENG, H. D., and CHEN, L. Q. Dynamic performance and parameter optimization of a half-vehicle system coupled with an inerter-based X-structure nonlinear energy sink. Applied Mathematics and Mechanics (English Edition), 45(1), 85–110 (2023) http://doi.org/10.1007/s10483-024-3070-7 |
| [20] | WANG, Y., ZHANG, T., YIN, Y., and WEI, X. H. Reducing shimmy oscillation of a dual-wheel nose landing gear based on torsional nonlinear energy sink. Nonlinear Dynamics, 112(6), 4027–4062 (2024) |
| [21] | DOU, J. X., YAO, H. L., CAO, Y. B., HAN, S. D., and BAI, R. X. Enhancement of bistable nonlinear energy sink based on particle damper. Journal of Sound and Vibration, 547, 117547 (2023) |
| [22] | YAO, H. L., CAO, Y. B., ZHANG, S. J., and WEN, B. C. A novel energy sink with piecewise linear stiffness. Nonlinear Dynamics, 94(3), 2265–2275 (2018) |
| [23] | ZHANG, S. T., ZHOU, J. X., DING, H., and WANG, K. Micro-vibration mitigation of a cantilever beam by one-third power nonlinear energy sinks. Aerospace Science and Technology, 153, 109409 (2024) |
| [24] | DING, H. and SHAO, Y. F. NES cell. Applied Mathematics and Mechanics (English Edition), 43(12), 1793–1804 (2022) https://doi.org/10.1007/s10483-022-2934-6 |
| [25] | RONCEN, T., MICHON, G., and MANET, V. Design and experimental analysis of a pneumatic nonlinear energy sink. Mechanical Systems and Signal Processing, 190, 110088 (2023) |
| [26] | AL-SHUDEIFAT, M. A. Highly efficient nonlinear energy sink. Nonlinear Dynamics, 76(4), 1905–1920 (2014) |
| [27] | CHEN, J. E., SUN, M., HU, W. H., ZHANG, J. H., and WEI, Z. C. Performance of non-smooth nonlinear energy sink with descending stiffness. Nonlinear Dynamics, 100(1), 255–267 (2020) |
| [28] | WANG, J. J., ZHENG, Y. Q., MA, Y. H., and WANG, B. Experimental study on asymmetric and bistable nonlinear energy sinks enabled by side tracks. Mechanical Systems and Signal Processing, 206, 110874 (2024) |
| [29] | ZENG, Y. C., DING, H., JI, J. C., and CHEN, L. Q. Theoretical and experimental study of a stable state adjustable nonlinear energy sink. Mechanical Systems and Signal Processing, 216, 111470 (2024) |
| [30] | GENG, X. F., DING, H., JING, X. J., MAO, X. Y., WEI, K. X., and CHEN, L. Q. Dynamic design of a magnetic-enhanced nonlinear energy sink. Mechanical Systems and Signal Processing, 185, 109813 (2023) |
| [31] | KREMER, D. and LIU, K. F. A nonlinear energy sink with an energy harvester: harmonically forced responses. Journal of Sound and Vibration, 410, 287–302 (2017) |
| [32] | AL-SHUDEIFAT, M. A., WIERSCHEM, N. E., BERGMAN, L. A., and VAKAKIS, A. F. Numerical and experimental investigations of a rotating nonlinear energy sink. Meccanica, 52(4-5), 763–779 (2016) |
| [33] | SAEED, A. S., NASAR, R. A., and AL-SHUDEIFAT, M. A. A review on nonlinear energy sinks: designs, analysis and applications of impact and rotary types. Nonlinear Dynamics, 111(1), 1–37 (2022) |
| [34] | CHEN, L. Q., LI, X., LU, Z. Q., ZHANG, Y. W., and DING, H. Dynamic effects of weights on vibration reduction by a nonlinear energy sink moving vertically. Journal of Sound and Vibration, 451, 99–119 (2019) |
| [35] | LI, X., DING, H., and CHEN, L. Q. Effects of weights on vibration suppression via a nonlinear energy sink under vertical stochastic excitations. Mechanical Systems and Signal Processing, 173, 109073 (2022) |
| [36] | LIU, S. W., PENG, G. L., and JIN, K. Towards accurate modeling of the Tachi-Miura origami in vibration isolation platform with geometric nonlinear stiffness and damping. Applied Mathematical Modelling, 103, 674–695 (2022) |
| [37] | FANG, H. B., CHANG, T. S., and WANG, K. W. Magneto-origami structures: engineering multi-stability and dynamics via magnetic-elastic coupling. Smart Materials and Structures, 29(1), 015026 (2020) |
| [38] | JI, J. C., LUO, Q. T., and YE, K. Vibration control based metamaterials and origami structures: a state-of-the-art review. Mechanical Systems and Signal Processing, 161, 107945 (2021) |
| [39] | YU, K. F., CHEN, Y. W., YU, C. Y., LI, P., REN, Z. H., ZHANG, J. R., and LU, X. Origami-inspire quasi-zero stiffness structure for flexible low-frequency vibration isolation. International Journal of Mechanical Sciences, 276, 109377 (2024) |
| [40] | YE, K. and JI, J. C. An origami inspired quasi-zero stiffness vibration isolator using a novel truss-spring based stack Miura-ori structure. Mechanical Systems and Signal Processing, 165, 108383 (2022) |
| [41] | YE, K. and JI, J. C. Dynamic analysis of the effects of self-weight induced structural and damping nonlinearity on the performance of an origami-inspired vibration isolator. Journal of Sound and Vibration, 547, 117538 (2023) |
| [42] | YE, K., JI, J. C., and FITCH, R. Further investigation and experimental study of an origami structure-based quasi-zero-stiffness vibration isolator. International Journal of Non-Linear Mechanics, 157, 104554 (2023) |
| [43] | ZANG, J., YUAN, T. C., LU, Z. Q., ZHANG, Y. W., DING, H., and CHEN, L. Q. A lever-type nonlinear energy sink. Journal of Sound and Vibration, 437, 119–134 (2018) |
| [44] | SUN, X. T., LV, Q., QIAN, J. W., and XU, J. Vibration isolation platform for large-amplitude-low-frequency excitation by parallel-stack-assembly design of Miura origamis. International Journal of Non-Linear Mechanics, 166, 104831 (2024) |
| [1] | Xinyu LIAN, Bing LIU, Huaxia DENG, Xinglong GONG. A vibration isolator with a controllable quasi-zero stiffness region based on nonlinear force design [J]. Applied Mathematics and Mechanics (English Edition), 2024, 45(8): 1279-1294. |
| [2] | Jiahao ZHOU, Jiaxi ZHOU, Hongbin PAN, Kai WANG, Changqi CAI, Guilin WEN. Multi-layer quasi-zero-stiffness meta-structure for high-efficiency vibration isolation at low frequency [J]. Applied Mathematics and Mechanics (English Edition), 2024, 45(7): 1189-1208. |
| [3] | Hongyan CHEN, Youcheng ZENG, Hu DING, Siukai LAI, Liqun CHEN. Dynamics and vibration reduction performance of asymmetric tristable nonlinear energy sink [J]. Applied Mathematics and Mechanics (English Edition), 2024, 45(3): 389-406. |
| [4] | Jinxin DOU, Zhenping LI, Hongliang YAO, Muchuan DING, Guochong WEI. Torsional vibration suppression and electromechanical coupling characteristics of electric drive system considering misalignment [J]. Applied Mathematics and Mechanics (English Edition), 2024, 45(11): 1987-2010. |
| [5] | Qingqing LIU, Shenlong WANG, Ge YAN, Hu DING, Haihua WANG, Qiang SHI, Xiaohong DING, Huijie YU. A human-sensitive frequency band vibration isolator for heavy-duty truck seats [J]. Applied Mathematics and Mechanics (English Edition), 2024, 45(10): 1733-1748. |
| [6] | Yong WANG, Peili WANG, Haodong MENG, Liqun CHEN. Dynamic performance and parameter optimization of a half-vehicle system coupled with an inerter-based X-structure nonlinear energy sink [J]. Applied Mathematics and Mechanics (English Edition), 2024, 45(1): 85-110. |
| [7] | Yang JIN, Tianzhi YANG. Enhanced vibration suppression and energy harvesting in fluid-conveying pipes [J]. Applied Mathematics and Mechanics (English Edition), 2023, 44(9): 1487-1496. |
| [8] | Hu DING, J. C. JI. Vibration control of fluid-conveying pipes: a state-of-the-art review [J]. Applied Mathematics and Mechanics (English Edition), 2023, 44(9): 1423-1456. |
| [9] | Shengtao ZHANG, Jiaxi ZHOU, Hu DING, Kai WANG, Daolin XU. Fractional nonlinear energy sinks [J]. Applied Mathematics and Mechanics (English Edition), 2023, 44(5): 711-726. |
| [10] | Weixing ZHANG, Wei ZHANG, Xiangying GUO. Vertical vibration control using nonlinear energy sink with inertial amplifier [J]. Applied Mathematics and Mechanics (English Edition), 2023, 44(10): 1721-1738. |
| [11] | A. MOSLEMI, M. R. HOMAEINEZHAD. Effects of viscoelasticity on the stability and bifurcations of nonlinear energy sinks [J]. Applied Mathematics and Mechanics (English Edition), 2023, 44(1): 141-158. |
| [12] | Xiaoye MAO, Mengmeng YIN, Hu DING, Xiaofeng GENG, Yongjun SHEN, Liqun CHEN. Modeling, analysis, and simulation of X-shape quasi-zero-stiffness-roller vibration isolators [J]. Applied Mathematics and Mechanics (English Edition), 2022, 43(7): 1027-1044. |
| [13] | Guoxin JIN, Zhenghao WANG, Tianzhi YANG. Cascaded quasi-zero stiffness nonlinear low-frequency vibration isolator inspired by human spine [J]. Applied Mathematics and Mechanics (English Edition), 2022, 43(6): 813-824. |
| [14] | Hu DING, Yufei SHAO. NES cell [J]. Applied Mathematics and Mechanics (English Edition), 2022, 43(12): 1793-1804. |
| [15] | Jian'en CHEN, Wei ZHANG, Jun LIU, Wenhua HU. Vibration absorption of parallel-coupled nonlinear energy sink under shock and harmonic excitations [J]. Applied Mathematics and Mechanics (English Edition), 2021, 42(8): 1135-1154. |
| Viewed | ||||||
|
Full text |
|
|||||
|
Abstract |
|
|||||


 Email Alert
Email Alert RSS
RSS