Applied Mathematics and Mechanics (English Edition) ›› 2024, Vol. 45 ›› Issue (11): 1929-1948.doi: https://doi.org/10.1007/s10483-024-3180-7
• Articles • Previous Articles Next Articles
Yu ZHANG1, Daming NIE1, Xuyao MAO2, Li LI3,*( )
)
Received:2024-05-17
Online:2024-11-03
Published:2024-10-30
Contact:
Li LI
E-mail:lili_em@hust.edu.cn
Supported by:2010 MSC Number:
Yu ZHANG, Daming NIE, Xuyao MAO, Li LI. A thermodynamics-consistent spatiotemporally-nonlocal model for microstructure-dependent heat conduction. Applied Mathematics and Mechanics (English Edition), 2024, 45(11): 1929-1948.

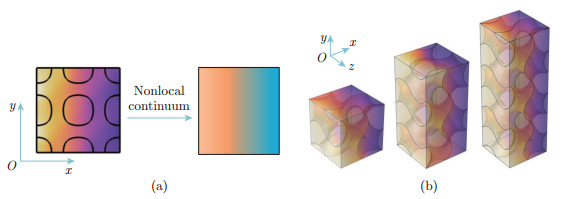
Fig. 1
Nonlocal steady-state heat conduction problem: (a) illustration of nonlocal homogenization and (b) illustration of 1D heat conduction with 3D microstructure (nonlocal) effect. The gyroid unit cell with 50% porosity is used as the 3D microstructure of structures with varying width. x is in the length direction, y is in the width direction, and z is in the height direction (color online)"
| 1 | KOVÁCS, R. Heat equations beyond Fourier: from heat waves to thermal metamaterials. Physics Reports, 1048, 1- 75 (2024) |
| 2 | ZENG, R., WANG, K., and LI, P. Special finite elements with arbitrarily-shaped holes for heat conduction analysis of porous materials. International Journal of Heat and Mass Transfer, 215, 124458 (2023) |
| 3 | SHIOMI, J., and MARUYAMA, S. Non-Fourier heat conduction in a single-walled carbon nanotube: classical molecular dynamics simulations. Physical Review B, 73 (20), 205420 (2006) |
| 4 | TZOU, D. Y. Macro-to Microscale Heat Transfer: the Lagging Behavior, 2nd ed., John Wiley and Sons, Pondicherry (2015) |
| 5 | PRASAD, V. S., and DAS, S. An experimental and theoretical investigation into the hyperbolic nature of axial dispersion in packed beds. International Journal of Heat and Mass Transfer, 45 (18), 3681- 3688 (2002) |
| 6 | AURIAULT, J. L. The paradox of Fourier heat equation: a theoretical refutation. International Journal of Engineering Science, 118, 82- 88 (2017) |
| 7 | CHEN, J., HE, J., PAN, D. K., WANG, X. T., YANG, N., ZHU, J. J., YANG, S. A., and ZHANG, G. Emerging theory and phenomena in thermal conduction: a selective review. Science China: Physics, Mechanics & Astronomy, 65 (11), 117002 (2022) |
| 8 | JOSEPH, D. D., and PREZIOSI, L. Heat waves. Reviews of Modern Physics, 61 (1), 41- 73 (1989) |
| 9 | CATTANEO, C. A form of heat-conduction equations which eliminates the paradox of instantaneous propagation. Comptes Rendus, 247, 431- 433 (1958) |
| 10 | VERNOTTE, P. Some possible complications in the phenomena of thermal conduction. Comptes Rendus, 252 (1), 2190- 2191 (1961) |
| 11 | AMENDOLA, G., FABRIZIO, M., GOLDEN, J. M., AMENDOLA, G., FABRIZIO, M., and GOLDEN, J. Thermodynamics of Materials with Memory, Springer, Cham (2021) |
| 12 | LI, Z. Y., MELLMANN, M., WANG, Y., MA, T. X., YAN, D., GOLUB, M. V., HOSSEINI, S. M., LIU, D. H., WEI, P. J., and ZHANG, C. Z. Non-Fourier heat conduction in 2D thermal metamaterials. Materials Today Communications, 38, 107828 (2024) |
| 13 | SERDYUKOV, S. A new version of extended irreversible thermodynamics and dual-phase-lag model in heat transfer. Physics Letters A, 281 (1), 16- 20 (2001) |
| 14 | XU, M. Thermodynamic basis of dual-phase-lagging heat conduction. Journal of Heat Transfer, 133 (4), 041401 (2011) |
| 15 | LI, B., JI, Q., WANG, J., WANG, C., and KADIC, M. Thermal conductivity and nonreciprocity in wrinkled monolayer graphene ring. Thin-Walled Structures, 195, 111523 (2024) |
| 16 | SHAO, D., XU, L., LI, P., and ZHOU, H. Two-dimensional thermoelastic damping models for circular micro/nanoplate resonators with nonlocal dual-phase-lagging effect of heat conduction. Thin-Walled Structures, 190, 110972 (2023) |
| 17 | ASHEGHI, M., LEUNG, Y., WONG, S., and GOODSON, K. Phonon-boundary scattering in thin silicon layers. Applied Physics Letters, 71 (13), 1798- 1800 (1997) |
| 18 | WANG, Z., ALANIZ, J. E., JANG, W., GARAY, J. E., and DAMES, C. Thermal conductivity of nanocrystalline silicon: importance of grain size and frequency-dependent mean free paths. Nano Letters, 11 (6), 2206- 2213 (2011) |
| 19 | HRYTSYNA, O., TOKOVYY, Y., and HRYTSYNA, M. Non-classical theory of electro-thermo-elasticity incorporating local mass displacement and nonlocal heat conduction. Mathematics and Mechanics of Solids, 29 (3), 539- 559 (2023) |
| 20 | HRYTSYNA, O., TOKOVYY, Y., and HRYTSYNA, M. Local gradient theory of dielectrics incorporating polarization inertia and flexodynamic effect. Continuum Mechanics and Thermodynamics, 35 (6), 2125- 2144 (2023) |
| 21 | CHEN, G. Non-Fourier phonon heat conduction at the microscale and nanoscale. Nature Reviews Physics, 3 (8), 555- 569 (2021) |
| 22 | KADIC, M., MILTON, G. W., VAN HECKE, M., and WEGENER, M. 3D metamaterials. Nature Reviews Physics, 1 (3), 198- 210 (2019) |
| 23 | LI, S., and LI, L. A homogenization method incorporating surface effect for thin metamaterial structure. International Journal of Engineering Science, 201, 104093 (2024) |
| 24 | PATNAIK, S., JOKAR, M., DING, W., and SEMPERLOTTI, F. On the role of the microstructure in the deformation of porous solids. npj Computational Materials, 7, 99- 105 (2023) |
| 25 | BACIGALUPO, A., and GAMBAROTTA, L. Identification of non-local continua for lattice-like materials. International Journal of Engineering Science, 159, 103430 (2021) |
| 26 | MEI, C. S., LI, L., LI, X. B., TANG, H. S., HAN, X. Z., WANG, X. L., and HU, Y. J. A nonlocality-based homogenization method for dynamics of metamaterials. Composite Structures, 295, 115716 (2022) |
| 27 | SHAAT, M., GHAVANLOO, E., and FAZELZADEH, S. A. Review on nonlocal continuum mechanics, physics, material applicability, and mathematics. Mechanics of Materials, 150, 103587 (2020) |
| 28 | JIANG, Y., LI, L., and HU, Y. A physically-based nonlocal strain gradient theory for crosslinked polymers. International Journal of Mechanical Sciences, 245, 108094 (2023) |
| 29 | OGAWA, S., YONEKURA, K., and SUZUKI, K. Multimaterial topology optimization of unsteady heat conduction problems based on discrete material optimization. International Journal of Heat and Mass Transfer, 225, 125353 (2024) |
| 30 | ZHU, H., PATNAIK, S., WALSH, T. F., JARED, B. H., and SEMPERLOTTI, F. Nonlocal elastic metasurfaces, enabling broadband wave control via intentional nonlocality. Proceedings of the National Academy of Sciences, 117 (42), 26099- 26108 (2020) |
| 31 | LI, S., ZHENG, W., and LI, L. Spatiotemporally nonlocal homogenization method for viscoelastic porous metamaterial structures. International Journal of Mechanical Sciences, 282, 109572 (2024) |
| 32 | LU, T., ZHENG, W., TANG, R., and LI, L. Beam-type acoustic black holes incorporating the microstructure-dependent nonlocal effect. Thin-Walled Structures, 197, 111662 (2024) |
| 33 | FEHÉR, A., and KOVÁCS, R. On the evaluation of non-Fourier effects in heat pulse experiments. International Journal of Engineering Science, 169, 103577 (2021) |
| 34 | BUFFERAND, H., CIRAOLO, G., GHENDRIH, P., LEPRI, S., and LIVI, R. Particle model for nonlocal heat transport in fusion plasmas. Physical Review E, 87 (2), 023102 (2013) |
| 35 | GUYER, R. A., and KRUMHANSL, J. Solution of the linearized phonon Boltzmann equation. Physical Review, 148 (2), 766- 778 (1966) |
| 36 | LEBON, G., JOU, D., CASAS-VAZQUEZ, J., and MUSCHIK, W. Weakly nonlocal and nonlinear heat transport in rigid solids. Journal of Non-Equilibrium Thermodynamics, 23 (2), 176- 191 (1998) |
| 37 | FOREST, S., and AIFANTIS, E. C. Some links between recent gradient thermo-elasto-plasticity theories and the thermomechanics of generalized continua. International Journal of Solids and Structures, 47 (25-26), 3367- 3376 (2010) |
| 38 | MONGIOVÍ, , M., S., and ZINGALES, M. A non-local model of thermal energy transport, the fractional temperature equation. International Journal of Heat and Mass Transfer, 67, 593- 601 (2016) |
| 39 | ZHOU, H., LI, P., and FANG, Y. Single-phase-lag thermoelastic damping models for rectangular cross-sectional micro- and nano-ring resonators. International Journal of Mechanical Sciences, 163, 105132 (2019) |
| 40 | DENG, W., LI, L., HU, Y., WANG, X., and LI, X. Thermoelastic damping of graphene nanobeams by considering the size effects of nanostructure and heat conduction. Journal of Thermal Stresses, 41 (9), 1182- 1200 (2018) |
| 41 | FEHÉR, A., LUKÁCS, N., SOMLAI, L., FODOR, T., SZUCS, M., FULOP, T., VAN, P., and KOVÁCS, R. Size effects and beyond-Fourier heat conduction in room-temperature experiments. Journal of Non-Equilibrium Thermodynamics, 46 (4), 403- 411 (2021) |
| 42 | LI, L., LIN, R., and HU, Y. Cross-section effect on mechanics of nonlocal beams. Archive of Applied Mechanics, 91, 1541- 1556 (2021) |
| 43 | ERINGEN, A. C. Nonlocal Continuum Field Theories, Springer Science & Business Media, New York (2002) |
| 44 | BAZANT, Z. P., and JIRASEK, M. Nonlocal integral formulations of plasticity and damage, survey of progress. Journal of Engineering Mechanics, 128 (11), 1119- 1149 (2002) |
| 45 | WANG, M., and PAN, N. Predictions of effective physical properties of complex multiphase materials. Materials Science and Engineering R-Reports, 63 (1), 1- 30 (2008) |
| 46 | BOGGARAPU, V., GUJJALA, R., OJHA, S., ACHARYA, S., BABU, P. V., CHOWDARY, S., and GARA, D. K. State of the art in functionally graded materials. Composite Structures, 262, 113596 (2021) |
| 47 | WANG, L., XU, J., and WANG, J. A peridynamic framework and simulation of non-Fourier and nonlocal heat conduction. International Journal of Heat and Mass Transfer, 118, 1284- 1292 (2018) |
| 48 | LI, L., LIN, R., and NG, T. Y. A fractional nonlocal time-space viscoelasticity theory and its applications in structural dynamics. Applied Mathematical Modelling, 84, 116- 136 (2020) |
| 49 | ERINGEN, A. C. On differential equations of nonlocal elasticity and solutions of screw dislocation and surface waves. Journal of Applied Physics, 54 (9), 4703- 4710 (1983) |
| 50 | NYÍRI, B. On the entropy current. Journal of Non-Equilibrium Thermodynamics, 16 (2), 179- 186 (1991) |
| 51 | MCBENNETT, B., BEARDO, A., NELSON, E. E., ABAD, B., FRAZER, T. D., ADAK, A., ESASHI, Y., LI, B. W., KAPTEYN, H. C., MURNANE, M. M., and KNOBLOCH, J. L. Universal behavior of highly confined heat flow in semiconductor nanosystems, from nanomeshes to metalattices. Nano Letters, 23 (6), 2129- 2136 (2023) |
| 52 | TAMMA, K. K., and ZHOU, X. Macroscale and microscale thermal transport and thermo-mechanical interactions, some noteworthy perspectives. Journal of Thermal Stresses, 21 (3-4), 405- 449 (1998) |
| [1] | K. CHANDAN, K. KARTHIK, K. V. NAGARAJA, B. C. PRASANNAKUMARA, R. S. VARUN KUMAR, T. MUHAMMAD. Radiative heat transfer analysis of a concave porous fin under the local thermal non-equilibrium condition: application of the clique polynomial method and physics-informed neural networks [J]. Applied Mathematics and Mechanics (English Edition), 2024, 45(9): 1613-1632. |
| [2] | Wei LU, Shuo CHEN, Zhiyuan YU, Jiayi ZHAO. Simulation of nanofluid natural convection based on single-particle hydrodynamics in energy-conserving dissipative particle dynamics (eDPD) [J]. Applied Mathematics and Mechanics (English Edition), 2024, 45(8): 1429-1446. |
| [3] | Shuo WANG, Anshuai WANG, Yansen WU, Xiaofeng LI, Yongtao SUN, Zhaozhan ZHANG, Qian DING, G. D. AYALEW, Yunxiang MA, Qingyu LIN. Ultra-wide band gap and wave attenuation mechanism of a novel star-shaped chiral metamaterial [J]. Applied Mathematics and Mechanics (English Edition), 2024, 45(7): 1261-1278. |
| [4] | Long ZHAO, Zeqi LU, Hu DING, Liqun CHEN. A viscoelastic metamaterial beam for integrated vibration isolation and energy harvesting [J]. Applied Mathematics and Mechanics (English Edition), 2024, 45(7): 1243-1260. |
| [5] | Zhou HU, Zhibo WEI, Yan CHEN, Rui ZHU. Reconfigurable mechanism-based metamaterials for ternary-coded elastic wave polarizers and programmable refraction control [J]. Applied Mathematics and Mechanics (English Edition), 2024, 45(7): 1225-1242. |
| [6] | Xingzhong WANG, Shiteng RUI, Shaokun YANG, Weiquan ZHANG, Fuyin MA. A low-frequency pure metal metamaterial absorber with continuously tunable stiffness [J]. Applied Mathematics and Mechanics (English Edition), 2024, 45(7): 1209-1224. |
| [7] | Wei WEI, Feng GUAN, Xin FANG. A low-frequency and broadband wave-insulating vibration isolator based on plate-shaped metastructures [J]. Applied Mathematics and Mechanics (English Edition), 2024, 45(7): 1171-1188. |
| [8] | Changqi CAI, Chenjie ZHU, Fengyi ZHANG, Jiaojiao SUN, Kai WANG, Bo YAN, Jiaxi ZHOU. Modeling and analysis of gradient metamaterials for broad fusion bandgaps [J]. Applied Mathematics and Mechanics (English Edition), 2024, 45(7): 1155-1170. |
| [9] | Yuxin YAO, Yuansheng MA, Fang HONG, Kai ZHANG, Tingting WANG, Haijun PENG, Zichen DENG. On Klein tunneling of low-frequency elastic waves in hexagonal topological plates [J]. Applied Mathematics and Mechanics (English Edition), 2024, 45(7): 1139-1154. |
| [10] | Chao WANG, Honggang ZHAO, Yang WANG, Jie ZHONG, Dianlong YU, Jihong WEN. Topology optimization of chiral metamaterials with application to underwater sound insulation [J]. Applied Mathematics and Mechanics (English Edition), 2024, 45(7): 1119-1138. |
| [11] | Yabin JING, Lifeng WANG, Yuqiang GAO. Mass-spring model for elastic wave propagation in multilayered van der Waals metamaterials [J]. Applied Mathematics and Mechanics (English Edition), 2024, 45(7): 1107-1118. |
| [12] | M. SAFI, M. VAKILIFARD, M. J. MAHMOODI. Frequency-dependent viscoelasticity effects on the wave attenuation performance of multi-layered periodic foundations [J]. Applied Mathematics and Mechanics (English Edition), 2024, 45(3): 407-424. |
| [13] | Jianguo CUI, Tianzhi YANG, Wenju HAN, Liang LI, Muqing NIU, Liqun CHEN. Tunable topological interface states via a parametric system in composite lattices with/without symmetric elements [J]. Applied Mathematics and Mechanics (English Edition), 2024, 45(12): 2055-2074. |
| [14] | Jinhui LIU, Yu XUE, Zhihong GAO, A. O. KRUSHYNSKA, Jinqiang LI. Actively tunable sandwich acoustic metamaterials with magnetorheological elastomers [J]. Applied Mathematics and Mechanics (English Edition), 2024, 45(11): 1875-1894. |
| [15] | Xingjian DONG, Shuo WANG, Anshuai WANG, Liang WANG, Zhaozhan ZHANG, Yuanhao TIE, Qingyu LIN, Yongtao SUN. Low-frequency bandgap and vibration suppression mechanism of a novel square hierarchical honeycomb metamaterial [J]. Applied Mathematics and Mechanics (English Edition), 2024, 45(10): 1841-1856. |
| Viewed | ||||||
|
Full text |
|
|||||
|
Abstract |
|
|||||


 Email Alert
Email Alert RSS
RSS