Applied Mathematics and Mechanics (English Edition) ›› 2025, Vol. 46 ›› Issue (10): 1983-2006.doi: https://doi.org/10.1007/s10483-025-3300-7
Previous Articles Next Articles
Yunting HAN, Hui HU, Haoran SUN, Xi SHI†( )
)
Received:2025-02-22
Revised:2025-08-08
Published:2025-09-30
Contact:
Xi SHI, E-mail: xishi@sjtu.edu.cnSupported by:2010 MSC Number:
Yunting HAN, Hui HU, Haoran SUN, Xi SHI. A new rope-sheave traction contact force model incorporating complex geometric features developed through parameter identification methods. Applied Mathematics and Mechanics (English Edition), 2025, 46(10): 1983-2006.
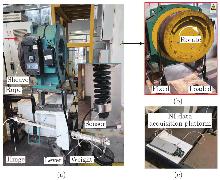
Fig. 2
The schematic of the experimental equipment used for the rope-sheave friction coefficient measurement. (a) Overall structure of the test apparatus; (b) illustration of the direction of the rotation of the sheave and loading of the wire rope; (c) NI data acquisition platform for the tension data collection (color online)"
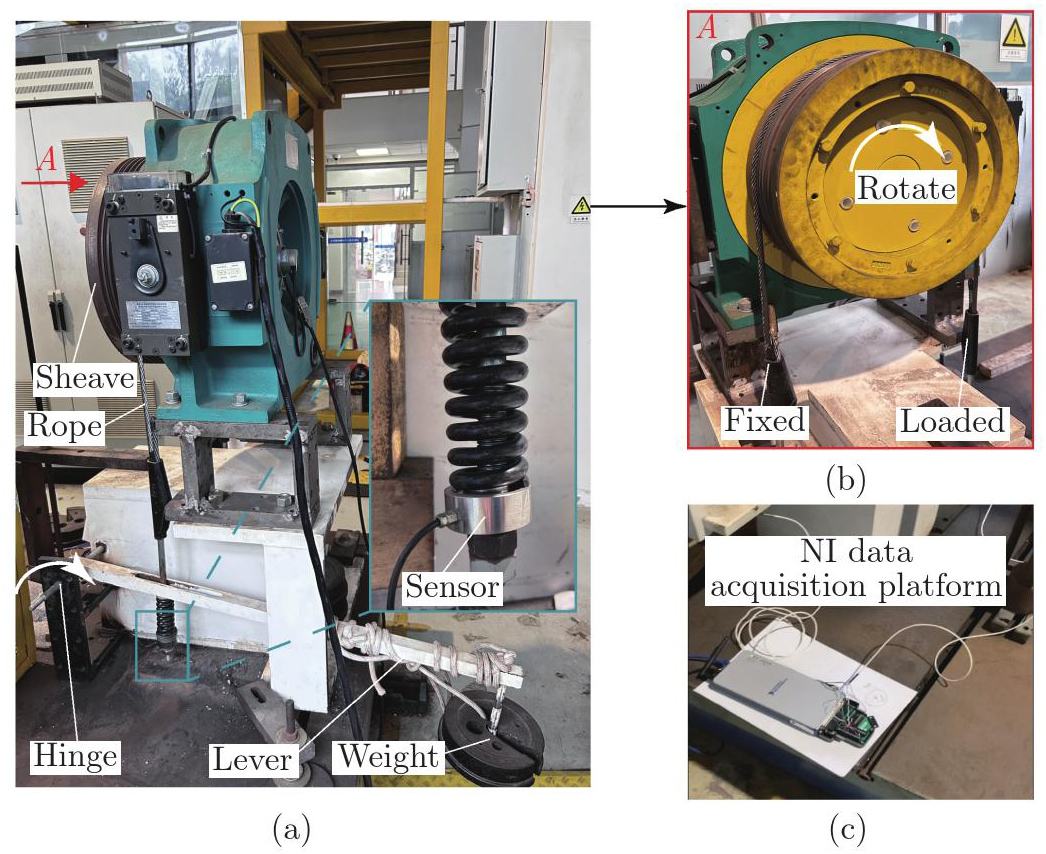
Fig. 9
Morphological characteristics of the elliptical contact zone at the rope-sheave contact interface obtained from the FE model. (a) Overall distribution of the contact zone along the wire rope; (b) the contact ellipse for a rope pitch length of 60.00 mm; (c) the contact ellipse when the pitch length is 61.75 mm; (d) the contact ellipse when the pitch length is 63.50 mm (color online)"
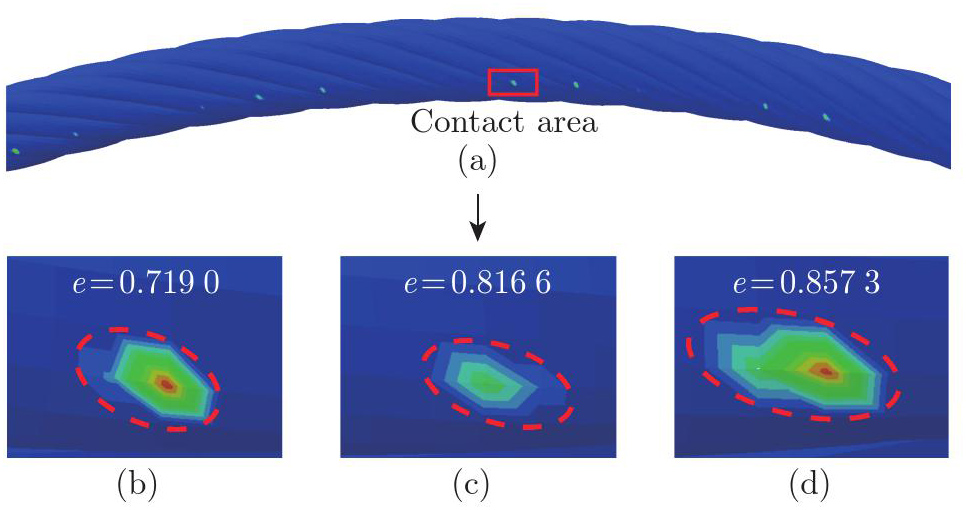

Fig. 11
Analysis of the variation of rope tension and the energy dissipation mechanism behind it in an ANCF framework using different contact force models. (a) The tension variations experienced at the fixed end of the rope during the emergency braking of the sheave, as modeled using different contact force models within the ANCF framework; (b) the power induced by the rope-sheave friction (color online)"
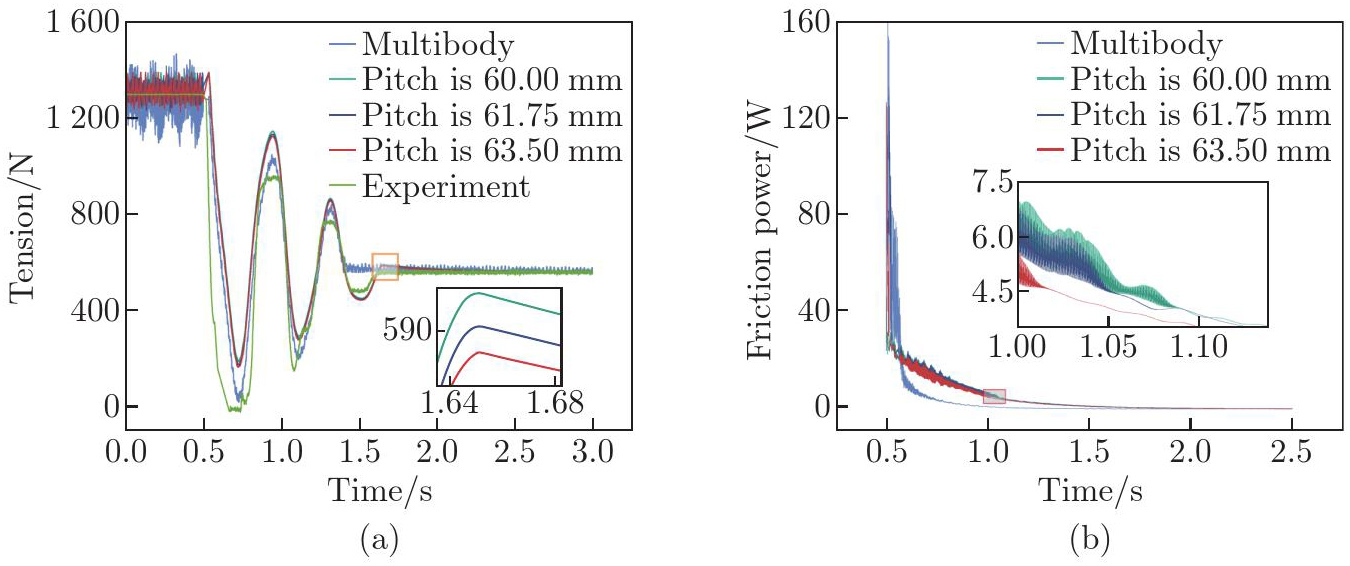
Fig. A1
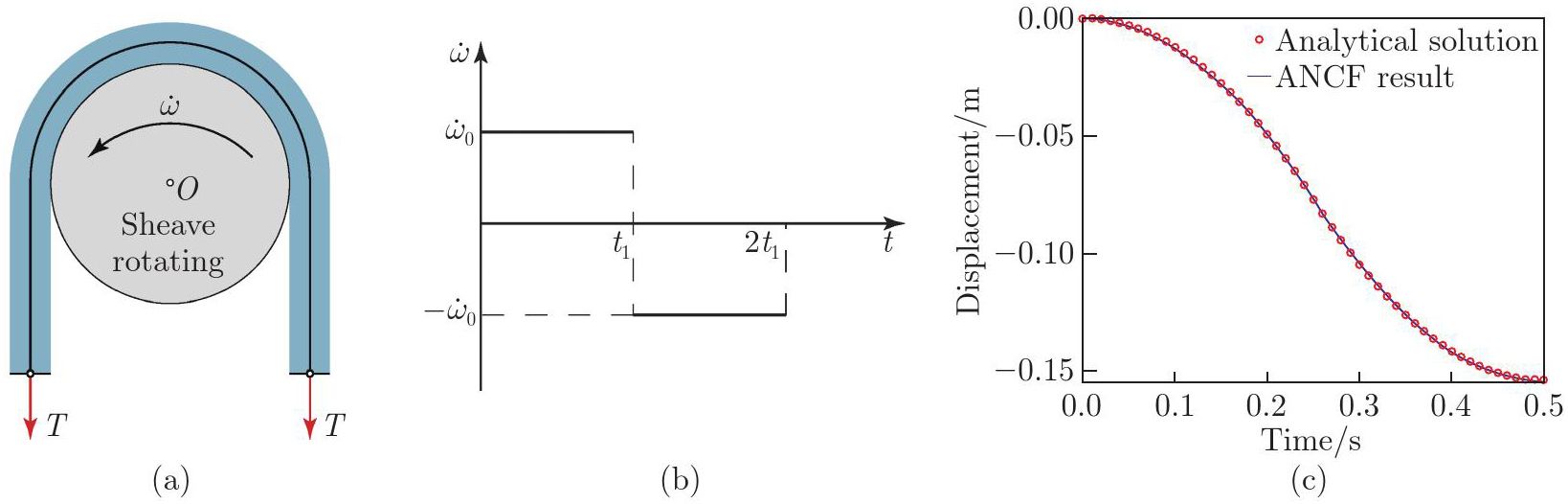
Evaluation of the accuracy of the ANCF model in calculating rope end displacement during uniform accelerated rotation of traction sheave. (a) The state of motion and the force diagram of the rope-sheave traction; (b) angular acceleration of the traction sheave as a function of time; (c) comparison of rope end displacements predicted by the ANCF model with the analytical solution (color online)"
| [1] | MA, J. and QIAN, L. Modeling and simulation of planar multibody systems considering multiple revolute clearance joints. Nonlinear Dynamics, 90(3), 1907–1940 (2017) |
| [2] | ZHENG, X., ZHANG, R., and WANG, Q. Comparison and analysis of two Coulomb friction models on the dynamic behavior of slider-crank mechanism with a revolute clearance joint. Applied Mathematics and Mechanics (English Edition), 39(9), 1239–1258 (2018) https://doi.org/10.1007/s10483-018-2371-9 |
| [3] | TIAN, Q., FLORES, P., and LANKARANI, H. M. A comprehensive survey of the analytical, numerical and experimental methodologies for dynamics of multibody mechanical systems with clearance or imperfect joints. Mechanism and Machine Theory, 122, 1–57 (2018) |
| [4] | YU, X., MATIKAINEN, M. K., HARISH, A. B., and MIKKOLA, A. Procedure for non-smooth contact for planar flexible beams with cone complementarity problem. Proceedings of the Institution of Mechanical Engineers, Part K: Journal of Multi-body Dynamics, 235(2), 179–196 (2021) |
| [5] | CORRAL, E., MORENO, R. G., GARCÍA, M. J. G., and CASTEJÓN, C. Nonlinear phenomena of contact in multibody systems dynamics: a review. Nonlinear Dynamics, 104(2), 1269–1295 (2021) |
| [6] | EYTELWEIN, J. A. Ausgaben Großtentheils Aus der Angewandten Mathematik, Freidrich Manrer, Berlin, Germany (1793) |
| [7] | JUNG, J. H., PAN, N., and KANG, T. J. Capstan equation including bending rigidity and non-linear frictional behavior. Mechanism and Machine Theory, 43(6), 661–675 (2008) |
| [8] | LU, Y. F., FAN, D. P., LIU, H., and HEI, M. Transmission capability of precise cable drive including bending rigidity. Mechanism and Machine Theory, 94, 132–140 (2015) |
| [9] | GRANDGEORGE, P., SANO, T. G., and REIS, P. M. An elastic rod in frictional contact with a rigid cylinder. Journal of the Mechanics and Physics of Solids, 164, 104885 (2022) |
| [10] | OBORIN, E. Belt-pulley interaction: role of the action line of friction forces. Acta Mechanica, 231(9), 3979–3987 (2020) |
| [11] | DAKEL, M., JEZEQUEL, L., and SORTAIS, J. L. Stationary and transient analyses of a pulley-belt system based on an Eulerian approach. Mechanism and Machine Theory, 128, 682–707 (2018) |
| [12] | MA, X., ZHANG, P., LI, N., SHI, X., and ZOU, H. Modeling and analysis for dynamic behavior of elevator traction system under the braking of safety gear. 2021 International Congress and Exposition of Noise Control Engineering, 263, 3738–3747 (2021) |
| [13] | MA, X., YANG, F., ZHANG, P., SHI, X., ZHANG, J., and ZOU, H. Effects of the braking performance for the safety gear on the dynamic behavior of the elevator traction system. Proceedings of the 28th International Congress on Sound and Vibration, Singapore (2022) |
| [14] | GUO, Y., ZHANG, D., CHEN, K., FENG, C., and GE, S. Longitudinal dynamic characteristics of steel wire rope in a friction hoisting system and its coupling effect with friction transmission. Tribology International, 119, 731–743 (2018) |
| [15] | GUO, Y., ZHANG, D., ZHANG, X., WANG, D., and WANG, S. A new transmission theory of “global dynamic wrap angle” for friction hoist combining suspended and wrapped wire rope. Applied Sciences, 10(4), 1305 (2020) |
| [16] | SHABANA, A. A. An overview of the ANCF approach, justifications for its use, implementation issues, and future research directions. Multibody System Dynamics, 58(3), 433–477 (2023) |
| [17] | HTUN, T. Z., SUZUKI, H., and GARCÍA-VALLEJO, D. On the theory and application of absolute coordinates-based multibody modeling of the rigid-flexible coupled dynamics of a deep-sea ROV-TMS integrated model. Ocean Engineering, 258, 111748 (2022) |
| [18] | PENG, Y., WEI, Y., and ZHOU, M. Efficient modeling of cable-pulley system with friction based on arbitrary-Lagrangian-Eulerian approach. Applied Mathematics and Mechanics (English Edition), 38(12), 1785–1802 (2017) https://doi.org/10.1007/s10483-017-2284-8 |
| [19] | ČEPON, G., MANIN, L., and BOLTEŽAR, M. Experimental identification of the contact parameters between a V-ribbed belt and a pulley. Mechanism and Machine Theory, 45(10), 1424–1433 (2010) |
| [20] | BULÍN, R., HAJŽMAN, M., and POLACH, P. Nonlinear dynamics of a cable-pulley system using the absolute nodal coordinate formulation. Mechanics Research Communications, 82, 21–28 (2017) |
| [21] | WESTIN, C. and IRANI, R. A. Modeling dynamic cable-sheave contact and detachment during towing operations. Marine Structures, 77, 102960 (2021) |
| [22] | ZHANG, H., GUO, J. Q., LIU, J. P., and REN, G. X. An efficient multibody dynamic model of arresting cable systems based on ALE formulation. Mechanism and Machine Theory, 151, 103892 (2020) |
| [23] | HEWLETT, J., ARBATANI, S., and KÖVECS, J. A fast and stable first-order method for simulation of flexible beams and cables. Nonlinear Dynamics, 99(2), 1211–1226 (2020) |
| [24] | NTARLADIMA, K., PIEBER, M., and GERSTMAYR, J. A model for contact and friction between beams under large deformation and sheaves. Nonlinear Dynamics, 111(22), 20643–20660 (2023) |
| [25] | BULÍN, R., DYK, Š., and HAJŽMAN, M. Nonlinear dynamics of flexible slender structures moving in a limited space with application in nuclear reactors. Nonlinear Dynamics, 104(4), 3561–3579 (2021) |
| [26] | COSTELLO, G. A. Theory of Wire Rope, Springer, New York (1997) |
| [27] | WU, W. and CAO, X. Mechanics model and its equation of wire rope based on elastic thin rod theory. International Journal of Solids and Structures, 102, 21–29 (2016) |
| [28] | ZHANG, Z. and WANG, X. Analytical modeling and approaches of multihelix cables incorporating with interwire mutual contacts. Applied Mathematics and Mechanics (English Edition), 45(9), 1633–1654 (2024) https://doi.org/10.1007/s10483-024-3147-6 |
| [29] | MEIER, C., GRILL, M. J., WALL, W. A., and POPP, A. Geometrically exact beam elements and smooth contact schemes for the modeling of fiber-based materials and structures. International Journal of Solids and Structures, 154, 124–146 (2018) |
| [30] | XING, E. and ZHOU, C. Analysis of the bending behavior of a cable structure under microgravity. International Journal of Mechanical Sciences, 114, 132–140 (2016) |
| [31] | DE MENEZES, E. A. W. and MARCZAK, R. J. Comparative analysis of different approaches for computing axial, torsional and bending stiffnesses of cables and wire ropes. Engineering Structures, 241, 112487 (2021) |
| [32] | FONTANARI, V., BENEDETTI, M., and MONELLI, B. D. Elasto-plastic behavior of a Warrington-Seale rope: experimental analysis and finite element modeling. Engineering Structures, 82, 113–120 (2015) |
| [33] | SHI, X., PAN, Y., and MA, X. Modeling and analysis of the rope-sheave interaction at traction interface. Journal of Applied Mechanics, 84(3), 031005 (2017) |
| [34] | WANG, D. and ARAÚJO, J. A. Tribo-fatigue behaviors of steel wire rope under bending fatigue with the variable tension. Wear, 428, 154–161 (2019) |
| [35] | HAN, Y., MA, X., ZHANG, G., HU, S., and SHI, X. Numerical investigation of rope-core elasticity effects on rope-sheave traction. Journal of the Brazilian Society of Mechanical Sciences and Engineering, 46(2), 90 (2024) |
| [36] | MA, J., CHEN, G., JI, L., QIAN, L., and DONG, S. A general methodology to establish the contact force model for complex contacting surfaces. Mechanical Systems and Signal Processing, 140, 106678 (2020) |
| [37] | MA, J., DONG, S., CHEN, G., PENG, P., and QIAN, L. A data-driven normal contact force model based on artificial neural network for complex contacting surfaces. Mechanical Systems and Signal Processing, 156, 107612 (2021) |
| [38] | MA, J., WANG, J., PENG, J., YIN, L., DONG, S., and TANG, J. Data-driven modeling for complex contacting phenomena via improved neural networks considering link switches. Mechanism and Machine Theory, 191, 105521 (2024) |
| [39] | QIN, Z., HUANG, Q., JIN, H., and XUE, H. Multi-body dynamics simulation of hoisting wire rope and its stress analysis. Journal of Northwestern Polytechnical University, 38(3), 485–493 (2020) |
| [40] | CHOU, D. Dahl Friction Modeling, S. B. Thesis, Massachusetts Institute of Technology (2004) |
| [41] | JOHANÅSTRÖM, K. and CANUDAS-DE-WIT, C. Revisiting the LuGre friction model. IEEE Control Systems Magazine, 28(6), 101–114 (2008) |
| [42] | LI, B., XIE, X., YU, B., LIAO, Y., and FAN, D. Data-driven friction modeling and compensation for rotary servo actuators. Frontiers of Mechanical Engineering, 19(6), 41 (2024) |
| [43] | JIA, T., LIU, J., WANG, Y., LI, C., and ZHANG, H. An improved LuGre friction model and its parameter identification of structural interface in thermal environment. Mechanical Systems and Signal Processing, 216, 111468 (2024) |
| [44] | HRABOVSKÝ, L., UČEŇ O., KUDRNA, L., ČEPICA, D., and FRYDRÝŠEK, K. Laboratory device detecting tensile forces in the rope and coefficient of friction in the rope sheave groove. Machines, 10(7), 590 (2022) |
| [45] | ZHU, H., ZHU, W. D., and FAN, W. Dynamic modeling, simulation and experiment of power transmission belt drives: a systematic review. Journal of Sound and Vibration, 491, 115759 (2021) |
| [46] | KUŠNEROVÁ, M., ŘEPKA, M., HARNIČ’AROVÁ, M., VALÍČEK, J., DANEL, R., KMEC, J., and PALKOVÁ, Z. A new way of measuring the belt friction coefficient using a digital servomotor. Measurement, 150, 107100 (2020) |
| [47] | MA, W. and LUBRECHT, A. A. Detailed contact pressure between wire rope and friction lining. Tribology International, 109, 238–245 (2017) |
| [48] | CHEN, C., GUO, Y., and MA, W. Fast solution of pressure and stress of dry contact using multigrid techniques. Processes, 10(8), 1441 (2022) |
| [49] | BARBER, J. R. Contact Mechanics, Springer International Publishing, Cham (2018) |
| [50] | JOHNSON, K. L. Contact Mechanics, Cambridge University Press, Cambridge (1987) |
| [1] | Xindan GUO, Qiming LIU, Xu HAN, Tao LI, Bin'an JIANG, Canwei CAI. High-precision numerical modeling of the projectile launch and failure mechanism analysis of projectile-borne components [J]. Applied Mathematics and Mechanics (English Edition), 2025, 46(5): 885-906. |
| [2] | Jing'ang ZHU, Yiheng XUE, Zishun LIU. A transfer learning enhanced physics-informed neural network for parameter identification in soft materials [J]. Applied Mathematics and Mechanics (English Edition), 2024, 45(10): 1685-1704. |
| [3] | Qiang YIN, Juntong CAI, Xue GONG, Qian DING. Local parameter identification with neural ordinary differential equations [J]. Applied Mathematics and Mechanics (English Edition), 2022, 43(12): 1887-1900. |
| [4] | Shuang LIU, Runze ZHANG, Qingyun WANG, Xiaoyan HE. Sliding mode synchronization between uncertain Watts-Strogatz small-world spatiotemporal networks [J]. Applied Mathematics and Mechanics (English Edition), 2020, 41(12): 1833-1846. |
| [5] | HUANG Yi;LIU Zeng-rong. TIME DOMAIN PARAMETERS IDENTIFICATION OF FOUNDATION-STRUCTURE INTERACTION SYSTEM [J]. Applied Mathematics and Mechanics (English Edition), 2005, 26(7): 855-864 . |
| [6] | YAO Zhi-yuan;WANG Feng-quan;ZHAO Chun-sheng. A METHOD OF ONLINE DAMAGE IDENTIFICATION FOR STRUCTURES BASED ON AMBIENT VIBRATION [J]. Applied Mathematics and Mechanics (English Edition), 2005, 26(2): 269-276 . |
| [7] | MA Jun-hai;CHEN Yu-shu;XIN Bao-gui. STUDY ON PREDICTION METHODS FOR DYNAMIC SYSTEMS OF NONLINEAR CHAOTIC TIME SERIES [J]. Applied Mathematics and Mechanics (English Edition), 2004, 25(6): 605-611. |
| [8] | GUO Da-li;LIU Ci-qun;ZHAO Jin-zhou. DYNAMIC PRODUCTION PREDICTION AND PARAMETER IDENTIFICATION FOR GAS WELL WITH VERTICAL FRACTURE [J]. Applied Mathematics and Mechanics (English Edition), 2002, 23(6): 627-633. |
| [9] | LI Shu;ZHANG Fang;WANG Bo;ZHANG Xiao-gu . PROPER APPLICATION OF A KIND OF MATRIX CON-STRUCTION METHOD IN PHYSICAL PARAMETER IDENTIFICATION OF DYNAMIC MODEL [J]. Applied Mathematics and Mechanics (English Edition), 2002, 23(5): 606-613. |
| [10] | MA Jun-hai;CHEN Yu-shu. STUDY ON THE PREDICTION METHOD OF LOW-DIMENSION TIME SERIES THAT ARISE FROM THE INTRINSIC NONLINEAR DYNAMIC [J]. Applied Mathematics and Mechanics (English Edition), 2001, 22(5): 501-509. |
| [11] | Li Shu;Zhuo Jiashou;Ren Qingwen . PARAMETER IDENTIFICATION OF DYNAMIC MODELS USING A BAYES APPROACH [J]. Applied Mathematics and Mechanics (English Edition), 2000, 21(4): 447-454. |
| [12] | Ma Junhai;Chen Yushu;Liu Zengrong. THE NON-LINEAR CHAOTIC MODEL RECONSTRUCTION FOR THE EXPERIMENTAL DATA OBTAINED FROM DIFFERENT DYNAMIC SYSTEM [J]. Applied Mathematics and Mechanics (English Edition), 1999, 20(11): 1214-1221. |
| Viewed | ||||||
|
Full text |
|
|||||
|
Abstract |
|
|||||


 Email Alert
Email Alert RSS
RSS