Structural vibration control using nonlinear damping amplifier friction vibration absorbers

doi:10.1007/s10483-025-3248-7

Abstract

Abstract:

This paper introduces damping amplifier friction vibration absorbers (DAFVAs), compound damping amplifier friction vibration absorbers (CDAFVAs), nested damping amplifier friction vibration absorbers (NDAFVAs), and levered damping amplifier friction vibration absorbers (LDAFVAs) for controlling the structural vibrations and addressing the limitations of conventional tuned mass dampers (TMDs) and friction-tuned mass dampers (FTMDs). The closed-form analytical solution for the optimized design parameters is obtained using the $H 2$ and $H ∞$ optimization approaches. The efficiency of the recently established closed-form equations for the optimal design parameters is confirmed by the analytical examination. The closed form formulas for the dynamic responses of the main structure and the vibration absorbers are derived using the transfer matrix formulations. The foundation is provided by the harmonic and random-white noise excitations. Moreover, the effectiveness of the innovative dampers has been validated through numerical analysis. The optimal DAFVAs, CDAFVAs, NDAFVAs, and LDAFVAs exhibit at least 30% lower vibration reduction capacity compared with the optimal TMD. To demonstrate the effectiveness of the damping amplification mechanism, the novel absorbers are compared with a conventional FTMD. The results show that the optimized novel absorbers achieve at least 91% greater vibration reduction than the FTMD. These results show how the suggested designs might strengthen the structure's resilience to dynamic loads.

Key words: damping amplifier friction vibration absorber (DAFVA), compound damping amplifier friction vibration absorber (CDAFVA), nested damping amplifier friction vibration absorber (NDAFVA), levered damping amplifier friction vibration absorber (LDAFVA), $H 2$ and $H ∞$ optimization approaches

2010 MSC Number:

O322

S. CHOWDHURY, S. ADHIKARI. Structural vibration control using nonlinear damping amplifier friction vibration absorbers. Applied Mathematics and Mechanics (English Edition), 2025, 46(5): 965-988.

TrendMD

Figures/Tables 18

Fig. 1

Fig. 2

Fig. 3

Fig. 4

Fig. 5

Fig. 6

Fig. 7

Fig. 8

Table 1

The structural system parameter for the SDOF system"

Primary structure	Governing system parameter	Value $ξ s$
SDOF	Damping ratio	0.01

Table 1

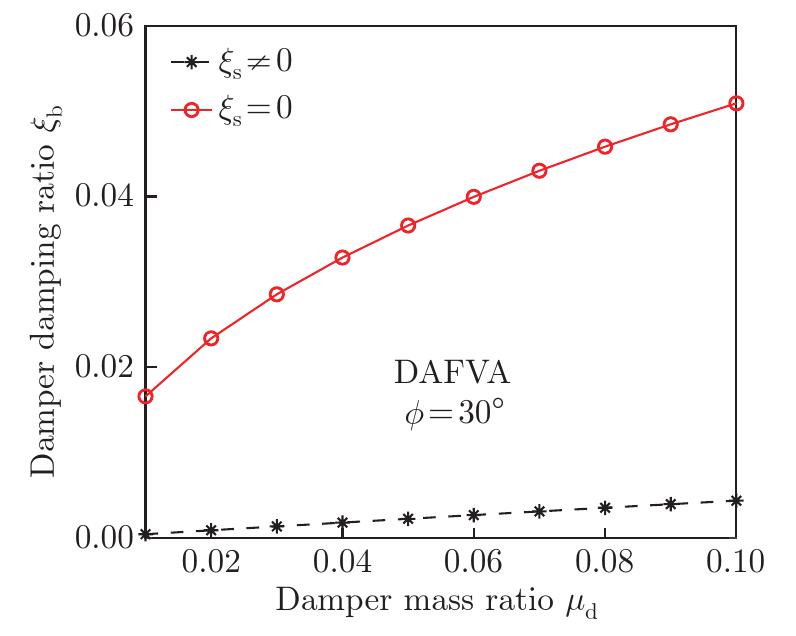
Table 2

The novel and conventional TMD's H2 optimized design parameters"

System	Reference	$H 2$ optimization
System	Reference	$κ b$	$ξ b$
DAFVA	Present	0.940 401	0.077 313 2
CDAFVA	Present	0.940 401	0.073 566 0
NDAFVA	Present	0.940 401	0.077 313 2
LDAFVA	Present	0.940 401	0.109 806 0
Conventional TMD1	Refs. [25] and [26]	$1 1 + μ ˜ d$	$μ ˜ d 2$
Conventional TMD2	Refs. [25] and [27]	$1 1 + μ ˜ d 2 + μ ˜ d 2$	$μ ˜ d (4 + 3 μ ˜ d) 8 (1 + μ ˜ d) (2 + μ ˜ d)$
Conventional TMD1: damper mass ratio $(μ ˜ d) = 0.05$ ; conventional TMD2: damper mass ratio $(μ ˜ d) = 0.05$ ; DAFVAs: damper mass ratio $(μ d) = 0.05$ , $ϕ = 40 o$ ; CDAFVAs: $μ d = 0.05$ , $ϕ = 40 o$ , $θ = 64 o$ ; NDAFVAs: $μ d = 0.05$ , $ϕ 1 = 40 o$ , $ϕ 2 = 45 o$ , $ϕ 3 = 45 o$ ; LDAFVAs: $μ d = 0.05$ , $b 1 / a 1 = 1$ , $b 2 / a 2 = 1$

Table 2

Fig. 9

Table 3

The values of each H∞ optimized design parameter for conventional and novel vibration absorbers"

System	Reference	$H ∞$ optimization
System	Reference	$κ b$	$ξ b$
DAFVA	Present	0.940 401	0.095 286 4
CDAFVA	Present	0.940 401	0.090 668 1
NDAFVA	Present	0.940 401	0.095 286 4
LDAFVA	Present	0.940 401	0.135 333 0
Conventional TMD1	Refs. [28] and [29]	$1 1 + μ ˜ d$	$3 μ ˜ d 8 (1 + μ ˜ d)$
Conventional TMD2	Ref. [30]	$1 1 + μ ˜ d$	$μ ˜ d 2 (1 + μ ˜ d)$
Conventional TMD1: damper mass ratio $(μ ˜ d) = 0.05$ ; conventional TMD2: damper mass ratio $(μ ˜ d) = 0.05$ ; DAFVAs: damper mass ratio $(μ d) = 0.05$ , $ϕ = 40 o$ ; CDAFVAs: $μ d = 0.05$ , $ϕ = 40 o$ , $θ = 64 o$ ; NDAFVAs: $μ d = 0.05$ , $ϕ 1 = 40 o$ , $ϕ 2 = 45 o$ , $ϕ 3 = 45 o$ ; LDAFVAs: $μ d = 0.05$ , $b 1 / a 1 = 1$ , $b 2 / a 2 = 1$

Table 3

Fig. 10

Fig. 11

Table 4

The optimal design parameters of FTMD"

System	Reference	Optimal parameter
System	Reference	$κ b$	$ξ b$
FTMD	Ref. [24]	1	0.029 1

Table 4

Fig. 12

Fig. 13

Fig. 14

References 31

[1]	LERNER, A. A. and CUNEFARE, K.Performance of mre-based vibration absorbers. Journal of Intelligent Material Systems and Structures, 19(5), 551–563 (2008)
[2]	LIU, K. and LIU, J.The damped dynamic vibration absorbers: revisited and new result. Journal of Sound and Vibration, 284(3-5), 1181–1189 (2005)
[3]	YANG, C., LI, D., and CHENG, L.Dynamic vibration absorbers for vibration control within a frequency band. Journal of Sound and Vibration, 330(8), 1582–1598 (2011)
[4]	WAGNER, N. and HELFRICH, R.Dynamic vibration absorbers and its applications. Journal of Sound and Vibration, 354, 6 (2017)
[5]	MORADI, H., BAKHTIARI-NEJAD, F., and MOVAHHEDY, M. R.Tuneable vibration absorber design to suppress vibrations: an application in boring manufacturing process. Journal of Sound and Vibration, 318(1-2), 93–108 (2008)
[6]	ALOTTA, G. and FAILLA, G.Improved inerter-based vibration absorbers. International Journal of Mechanical Sciences, 192, 106087 (2021)
[7]	CERA, M., CIRELLI, M., PENNESTR, E., and VALENTINI, P. P.Design analysis of torsichrone centrifugal pendulum vibration absorbers. Nonlinear Dynamics, 104, 1023–1041 (2021)
[8]	MAHÉ, V., RENAULT, A., GROLET, A., MAHÉ, H., and THOMAS, O.On the dynamic stability and efficiency of centrifugal pendulum vibration absorbers with rotating pendulums. Journal of Sound and Vibration, 536, 117157 (2022)
[9]	LI, H., TOUZÉ, C., PELAT, A., and GAUTIER, F.Combining nonlinear vibration absorbers and the acoustic black hole for passive broadband flexural vibration mitigation. International Journal of Non-Linear Mechanics, 129, 103558 (2021)
[10]	MAYET, J., ACAR, M. A., and SHAW, S. W.Effective and robust rocking centrifugal pendulum vibration absorbers. Journal of Sound and Vibration, 527, 116821 (2022)
[11]	GOMEZ, E. R., ARTEAGA, I. L., and KARI, L.Normal-force dependant friction in centrifugal pendulum vibration absorbers: simulation and experimental investigations. Journal of Sound and Vibration, 492, 115815 (2021)
[12]	CHANG, Y., ZHOU, J., WANG, K., and XU, D.A quasi-zero-stiffness dynamic vibration absorber. Journal of Sound and Vibration, 494, 115859 (2021)
[13]	YOU, T., ZHOU, J., THOMPSON, D. J., GONG, D., CHEN, J., and SUN, Y.Vibration reduction of a high-speed train floor using multiple dynamic vibration absorbers. Vehicle System Dynamics, 60(9), 2919–2940 (2022)
[14]	CHOWDHURY, S. and BANERJEE, A.The impacting vibration absorbers. Applied Mathematical Modelling, 127, 454–505 (2024)
[15]	SU, N., CHEN, Z., XIA, Y., and BIAN, J.Hybrid analytical h-norm optimization approach for dynamic vibration absorbers. International Journal of Mechanical Sciences, 264, 108796 (2024)
[16]	SU, N., BIAN, J., PENG, S., CHEN, Z., and XIA, Y.Analytical optimal design of inerter-based vibration absorbers with negative stiffness balancing static amplification and dynamic reduction effects. Mechanical Systems and Signal Processing, 192, 110235 (2023)
[17]	ZHANG, Y., CHENG, J., XU, W., WANG, C., LIU, J., LI, Y., and YANG, S.Particle damping vibration absorber and its application in underwater ship. Journal of Vibration Engineering & Technologies, 11(5), 2231–2248 (2023)
[18]	GUO, M., TANG, L., WANG, H., LIU, H., and GAO, S.A comparative study on transient vibration suppression of magnetic nonlinear vibration absorbers with different arrangements. Nonlinear Dynamics, 111(18), 16729–16776 (2023)
[19]	SU, N., BIAN, J., CHEN, Z., and XIA, Y.A novel 550 lever-type inerter-based vibration absorber. International Journal of Mechanical Sciences, 254, 108440 (2023)
[20]	ZHAO, C., ZHANG, K., ZHAO, P., and DENG, Z.Finite-amplitude nonlinear waves in inertial amplification metamaterials: theoretical and numerical analyses. Journal of Sound and Vibration, 560, 117802 (2023)
[21]	ZHAO, C., ZHANG, K., ZHAO, P., HONG, F., and DENG, Z.Bandgap merging and backward wave propagation in inertial amplification metamaterials. International Journal of Mechanical Sciences, 250, 108319 (2023)
[22]	MA, H., CHENG, Z., SHI, Z., and MARZANI, A.Structural vibration mitigation via an inertial amplification mechanism based absorber. Engineering Structures, 295, 116764 (2023)
[23]	SETTIMI, V., LEPIDI, M., and BACIGALUPO, A.Analytical spectral design of mechanical metamaterials with inertia amplification. Engineering Structures, 274, 115054 (2023)
[24]	GEWEI, Z. and BASU, B.A study on friction-tuned mass damper: harmonic solution and statistical linearization. Journal of Vibration and Control, 17(5), 721–731 (2011)
[25]	WARBURTON, G. B.Optimum absorber parameters for various combinations of response and excitation parameters. Earthquake Engineering & Structural Dynamics, 10(3), 381–401 (1982)
[26]	ZILLETTI, M., ELLIOTT, S. J., and RUSTIGHI, E.Optimisation of dynamic vibration absorbers to minimise kinetic energy and maximise internal power dissipation. Journal of Sound and Vibration, 331(18), 4093–4100 (2012)
[27]	IWATA, Y.On the construction of the dynamic vibration absorbers. Japanese Society of Mechanical Engineering, 820(8), 150–152 (1982)
[28]	ORMONDROYD, J. and DEN HARTOG, J. P.The theory of the dynamic vibration absorber. Journal of Fluids Engineering, 49(2), 021007 (1928)
[29]	NISHIHARA, O. and ASAMI, T.Closed-form solutions to the exact optimizations of dynamic vibration absorbers (minimizations of the maximum amplitude magnification factors). Journal of Vibration and Acoustics, 124(4), 576–582 (2002)
[30]	KRENK, S.Frequency analysis of the tuned mass damper. Journal of Applied Mechanics, 72, 936–942 (2005)
[31]	KIUREGHIAN, A. D. and NEUENHOFER, A.Response spectrum method for multi-support seismic excitations. Earthquake Engineering & Structural Dynamics, 21(8), 713–740 (1992)